迷宮密封結構設計優化

劉勇，梁崇治

(東方汽輪機有限公司，四川德陽，618000)

迷宮密封結構設計優化

劉勇，梁崇治

(東方汽輪機有限公司，四川德陽，618000)

耦合Kriging代理模型、迷宮密封參數化方法和自適應差分進化算法，在數值驗證的基礎上，完成了某迷宮式密封多目標魯棒性設計優化。優化時，選取壓比和密封間隙作為不確定性變量，同時選取齒厚等10個幾何參數作為優化變量，以迷宮密封泄漏量的均值及其方差最小為目標，進行多目標優化。優化后，在給定壓比和間隙條件下，最優設計泄漏量降低了29.85%，在壓比及間隙同時變化時，密封性能提升同樣明顯，從而驗證了多目標設計優化方法的正確性。

迷宮式密封，多目標優化，Kriging代理模型

0 引言

迷宮式密封由于壽命長、結構簡單、非接觸式等優點被廣泛應用于葉輪機械中[1]。密封中的泄漏損失會影響葉輪機械的效率及輸出功率。迷宮密封中流動現象復雜，其泄漏特性受到運行工況、結構參數等多種因素的影響。因此，采用優化方法以提高密封的性能是當前常用的手段。Schramm等[2]采用模擬退火優化算法對某三齒階梯迷宮密封進行了優化，使得泄漏量降低了10%。Braun等[3]提出了針對不同類型的迷宮密封的通用優化工具。Wang等[4]采用徑向基函數優化了某離心壓氣機的迷宮密封，優化后，密封的泄漏量顯著降低，同時葉輪的等熵效率提高了2%。Cremanns等[5]采用自主研發的混合響應面方法，以降低密封泄漏量和總焓降為目標，對某迷宮密封進行了多目標優化。

值得注意的是，密封齒的設計加工及運行過程存在諸多不確定性。首先，熱脹冷縮以及幾何加工誤差都會造成密封齒間隙相對設計值產生較大偏差，從而嚴重影響密封性能。另外，由于汽輪機各級組進出口壓力會發生波動，級前后壓比發生變化，對汽輪機密封性能也會產生較大影響。如何減輕上述由于加工、運行工況乃至環境變化所導致的不確定因素對汽輪機性能的影響，設計出適用范圍廣、魯棒性好的密封結構，是當前設計中的一個難點。

近年來，關于魯棒性（穩健性）設計優化的研究，因其對工程實際的重要意義而受到了廣泛的關注。在確定性優化中，是以提高產品的名義性能為目標，而未能考慮到加工、運行等過程中的不確定性的影響。魯棒性設計優化是追求產品的性能穩健性，降低性能受外界不確定因素影響的優化方法[6]。本文將Kriging代理模型[7]與多目標進化算法[8]相結合，以泄漏量的均值和方差作為目標函數，對迷宮式密封進行多目標設計優化。

1 多目標設計優化方法

1.1 迷宮密封多目標設計優化流程

耦合迷宮密封參數化方法、Kriging響應面以及自適應多目標差分進化算法（SMODE），發展了多目標設計優化方法，對迷宮齒型密封進行了多目標設計優化，如圖1所示。該方法包括4個階段，首先在空間均勻采樣的基礎上，采用CFD進行性能評估；其次利用Kriging響應面建立輸入與輸出之間的近似模型；接下來利用自適應多目標差分進化算法，以性能函數均值和方差作為目標函數開展多目標優化；最后，通過流場分析闡明最優設計泄漏量降低的本質原因。

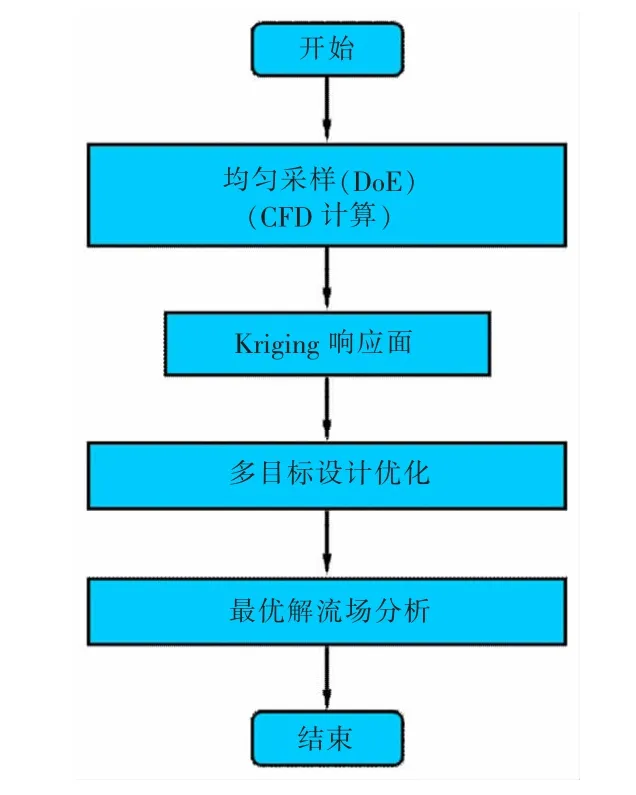
圖1 多目標設計優化流程

1.2 迷宮密封參數化方法

基于參考設計的迷宮齒型密封，本文進一步考慮了斜齒的傾角、根部的倒角以及頂部的型線，密封進出口的凹槽以及出口處的凸臺等結構對于密封性能的影響，建立的迷宮齒型密封參數化方法如圖2所示。

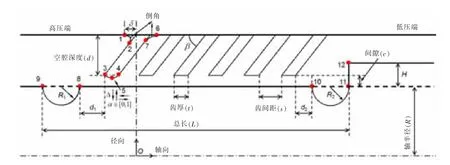
圖2 迷宮密封參數化方法

根據相關經驗，選取齒厚t、傾角β、倒角半徑δ、進口凹槽位置d1、進口凹槽半徑R1、出口凹槽位置d2、出口凹槽半徑R2、控制點5（a，Δ）共10個變量作為優化變量，選取間隙c和進出口壓比PR作為不確定性變量，而空腔的高度d及密封軸向總長L保持不變，如表1所示。

表1 設計變量

1.3 優化目標與約束條件

本文選取12個設計變量對迷宮齒型密封進行魯棒性多目標設計優化。其中，密封齒間隙和壓比作為不確定性變量，服從均勻分布；其余10個設計變量如齒厚、倒角半徑等作為優化變量。優化過程中，選取在密封齒間隙和壓比變化時密封平均泄漏量最小，并且泄漏量方差變化最小為目標函數，進行多目標設計優化。考慮到密封齒結構的特點，對齒厚與密封齒間距之間的關系進行約束，相應的表達式如下:

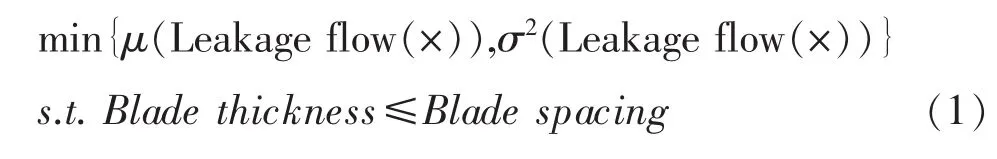
2 設計優化實例

2.1 數值計算方法

2.1.1 幾何模型

圖3給出了文獻[9]中某典型迷宮密封的幾何模型，本文將其作為參考設計，其具體幾何參數如表2所示。

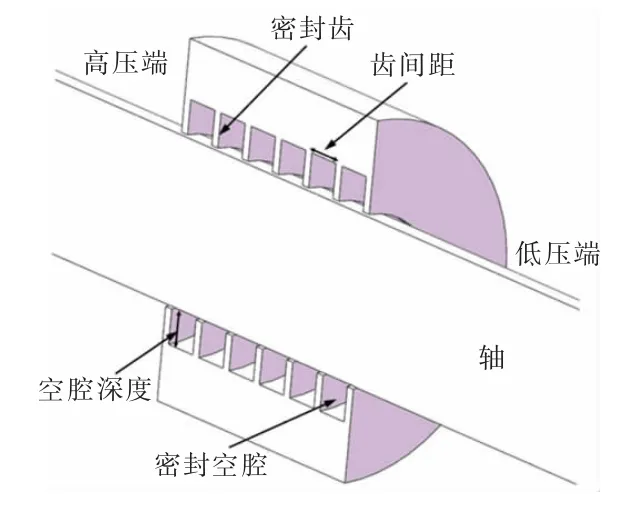
圖3 某典型迷宮密封的幾何模型

表2 參考設計的幾何參數

2.1.2 計算模型和邊界條件

本文采用商業軟件CFX求解RANS方程，預測迷宮密封的泄漏特性。湍流模型采用標準k-ε模型。計算中，考慮到周期性，取一部分弧段作為研究對象，弧段的兩側采用旋轉周期性邊界，計算模型如圖4所示。

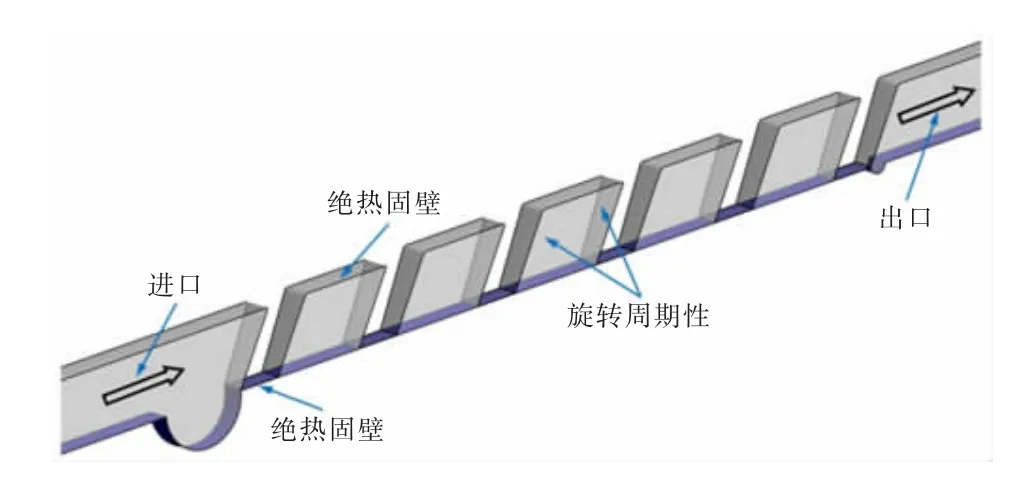
圖4 計算模型

進口給定總溫、總壓，出口給定平均靜壓，工質采用理想氣體。計算不同壓比時，改變進口總壓，其余保持不變，表3給出了壓比PR=0.367時的邊界條件。其中，壓比的定義為出口靜壓與進口總壓之比。

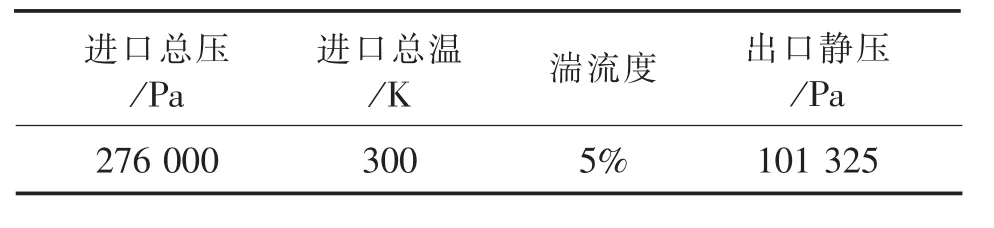
表3 PR=0.367時的邊界條件

計算的收斂標準為:動量方程殘差達到10-6數量級，質量方程殘差小于10-6數量級，進出口流量相差小于0.1%。

2.1.3 計算網格

本文采用ICEM軟件生成結構化網格，計算網格如圖5所示。為了提高網格質量，在倒角區域和凹槽區域采用O型網格剖分，其余區域采用H型網格剖分。對壁面網格進行加密，保證y+滿足湍流模型的要求。在節流間隙處沿徑向布置12個網格節點，以捕捉間隙內復雜的流動特征。經過網格無關性驗證，最終網格規模確定為65萬。

圖5 計算網格

2.2 數值方法驗證

圖6給出了不同壓比下，數值計算的泄漏量與實驗值的對比，可以看出，當壓比較小時，計算值偏低；當壓比較大時，計算值偏高；在中等壓比時，兩者吻合最好，其中，最大誤差小于14.5%，說明本文所采用的數值計算方法是正確、可行的。

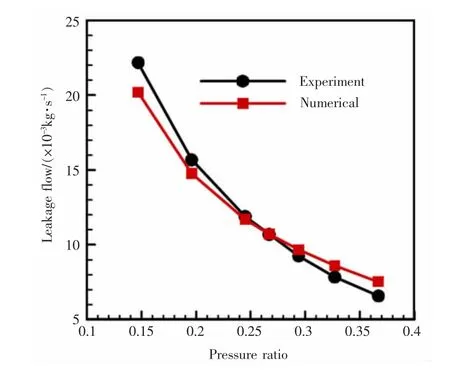
圖6 數值驗證結果

2.3 優化結果分析

圖7給出了多目標優化后得到的Pareto最優解集，優化后，迷宮密封泄漏量的均值和方差均顯著降低。

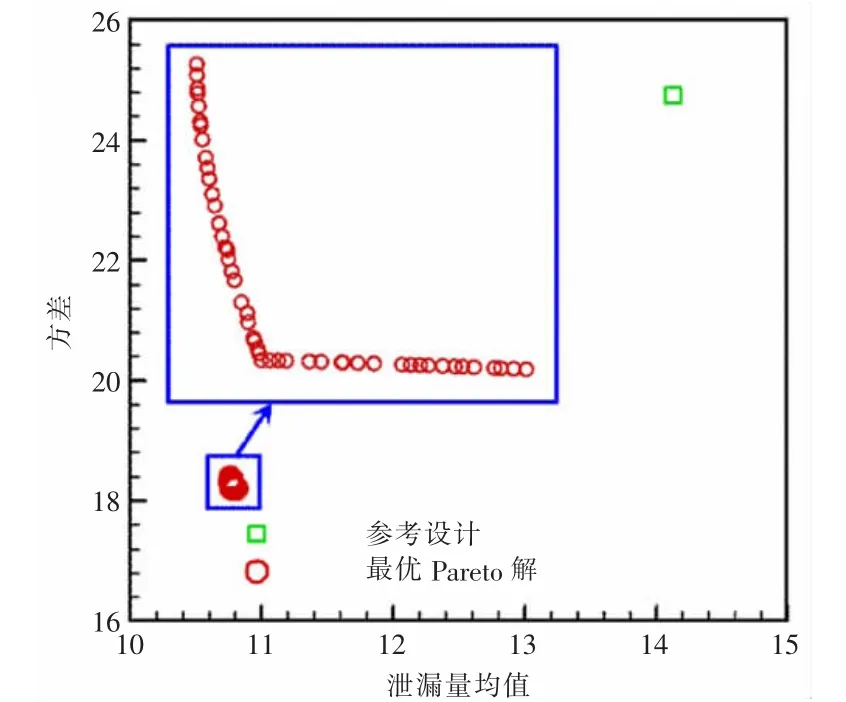
圖7 Pareto最優解集

圖8給出了優化前、后的型線對比。其中，t、Δ、R1取極大值，R2、β、d1、d2取極小值，而倒角半徑δ和凸臺高度H取中間值。

圖8 優化前后幾何對比

圖9給出了優化前后第一個齒總壓分布，可以看出，齒厚t越大，節流間隙內的節流效應越強，導致更多的動能轉化為熱能，因而最優設計密封齒出口處的總壓更低。

圖9 優化前、后第一個齒處總壓分布

圖10給出了優化前、后最后一個齒處的馬赫數分布，可以看出，齒厚越大，最后一個齒間隙出口的馬赫數越低，因而最優設計泄漏量越低。

圖10 優化前、后最后一個齒處馬赫數分布

圖11給出了優化前、后不同位置處馬赫數的分布，可以看出優化后，節流間隙處的速度分布明顯不同于參考設計。因為Δ導致此處的流動會經歷一個先收縮再擴張的過程，有利于節流效應的產生，降低優化設計的泄漏量。

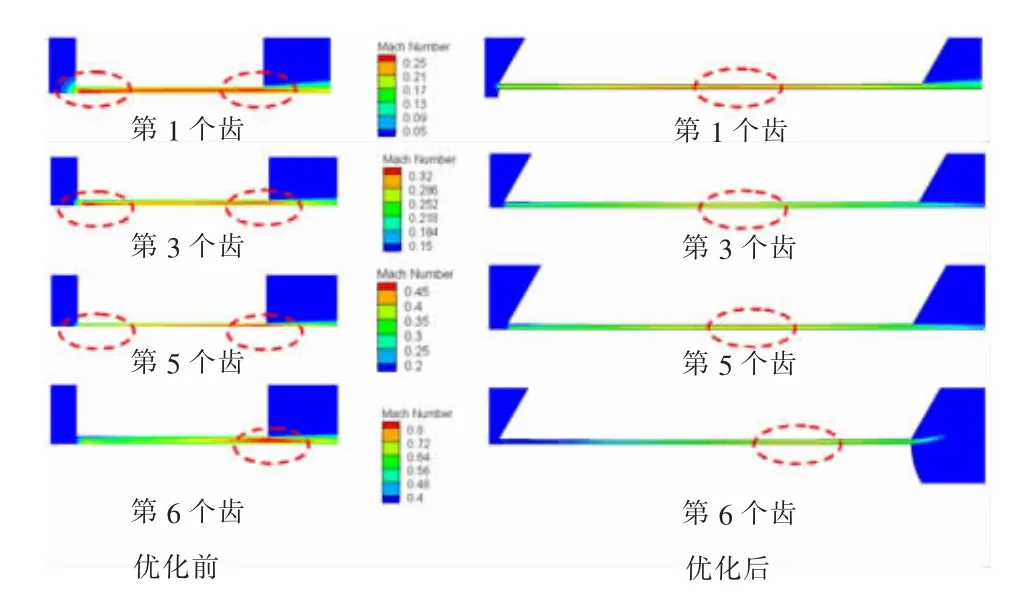
圖11 優化前、后不同位置處馬赫數分布

圖12比較了優化前、后第2個齒附近的馬赫數和流線分布，可知齒的傾斜改變了齒入口處的速度分布，有利于降低泄漏量。

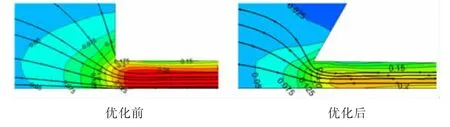
圖12 優化前、后第2個齒附近馬赫數和流線分布

表4定量對比了魯棒性優化前、后密封的總體性能，近似模型所預測的泄漏量與CFD計算的結果相差在3%以內，從而驗證了近似模型的可靠性。優化后，最優設計相對參考設計的泄漏量均值降低23.64%，方差降低26.39%。將壓比PR和節流間隙c固定時，泄漏量降低30%左右，表明最優設計相對參考設計密封性能明顯提高。

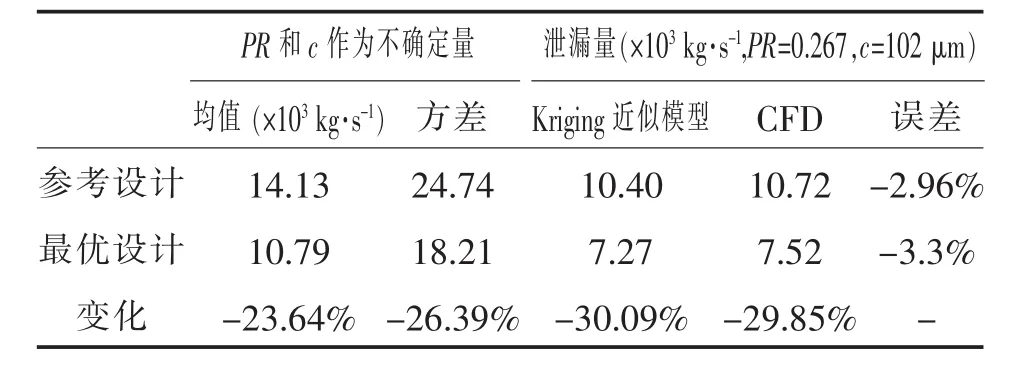
表4 優化前/后密封總體性能比較

圖13比較了不同壓比時優化前、后的泄漏量，可知，不同壓比時優化后的泄漏量相比于參考設計均降低，且壓比越小時，降低越明顯。從圖14可知，不同節流間隙時，優化后的泄漏量均降低，且節流間隙越大，降低越明顯。從而驗證了魯棒性設計優化的正確性和有效性。

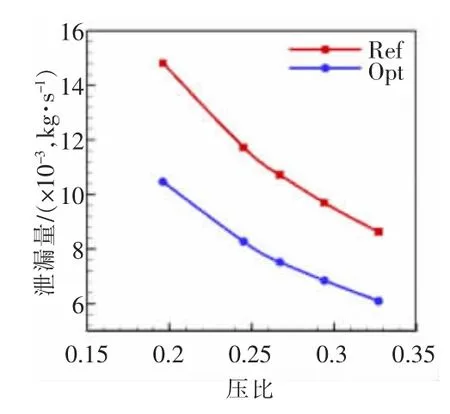
圖13 不同壓比時性能比較

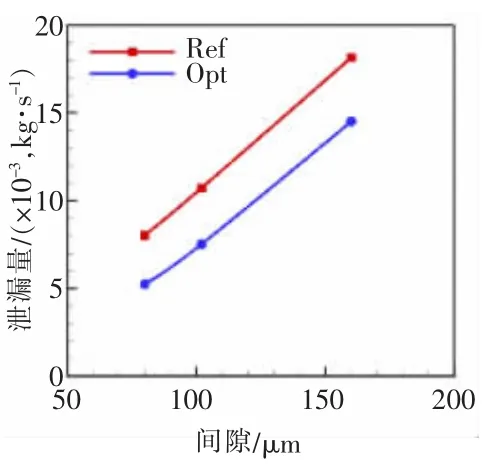
圖14 不同節流間隙時性能比較

3 結論

本文耦合基于Kriging代理模型的魯棒性多目標優化方法、不確定性量化方法，帶有復雜結構的迷宮齒型密封參數化方法和三維RANS方程求解技術，建立了迷宮齒型密封魯棒性多目標設計優化方法。

基于該方法，本文完成了迷宮齒型密封魯棒性多目標優化。優化后，最優設計相對參考設計的泄漏量均值降低23.64%，方差降低26.39%。將壓比PR和節流間隙c固定時，泄漏量降低30%左右，表明優化后迷宮密封性能明顯提高。

[1]We Soto E A,Childs D W.Experimental rotordynamic coefficient results for(a)a labyrinth seal with and without shunt injection and(b)a honeycomb seal[J].Journal of Engineering for Gas Turbines and Power,1999,121(1)：153-159.

[2]Schramm V,Denecke J,Kim S,et al.Shape optimization of a labyrinth seal applying the simulated annealing method[J]. International Journal of Rotating Machinery,2004,10(5)：365-371.

[3]Braun E,Dullenkopf K,Bauer H J.Optimization of labyrinth seal performance combining experimental,numerical and data mining methods[C].ASME Paper,GT2012-68077.

[4]Wang Z,Xu L,Xi G.Numerical investigation on the labyrinth seal design for a low flow coefficient centrifugal compressor[C].ASME Paper,GT2010-23096.

[5]Cremanns K,Roos D,Hecker S,et al.Efficient multi-objective optimization of labyrinth seal leakage in steam turbines based on hybrid surrogate model[C].ASME Paper, GT2016-57457.

[6]Park G J,Lee T H,Lee K H,et al.Robust Design：An Overview[J].AIAA Journal,2006,44(1)：181-191.

[7]郭振東，宋立明，李軍，等.基于子元模型的全局優化與設計空間知識挖掘方法[J]，推進技術，2015，36(2)：207-216.

[8]Song Liming,Luo Chang,Li Jun,et al.Automated Multiobjective and Multidisciplinary Design Optimization of a Transonic Turbine Stages[J].Journal of Power and Energy, 2012,226(2)：262-276.

[9]Gamal A J,Vance J M.Labyrinth seal leakage tests：tooth profile,tooth thickness and eccentricity effects[J].Journal of Engineering for Gas Turbines and Power,2008,130(1)：012510.

Shape Optimization of a Labyrinth Seal Configuration

Liu Yong，Liang Chongzhi

（Dongfang Turbine Co.,Ltd.,Deyang Sichuan,618000）

A multi-objective robust optimization method is proposed and implemented for the design of a labyrinth seal upon numerical validation.This method combines the Kriging surrogate model with parameterization method of a labyrinth seal,and selfadaptive multi-objective differential evolution algorithm（SMODE）as well.The multi-objective optimization is conducted for minimizing averaged leakage flow with minimum variance.In the optimization process,pressure ratio and seal clearance are set as uncertainty variables,and other 10 geometrical parameters are set as optimization variables.After optimization,the leakage flow rate of the optimal solution is reduced by 29.85%when pressure ratio and seal clearance are set as constant.And such smaller leakage flow maintained when pressure ratio and seal clearance are varied.Therefore,the correctness and effectiveness of the proposed method is demonstrated.

labyrinth seal,multi-objective optimization,Kriging surrogate model

TK402

A

1674-9987（2017）02-0016-05

10.13808/j.cnki.issn1674-9987.2017.02.005

劉勇（1977-），男，工學學士，工程師，畢業于重慶工學院機械制造及自動化專業，主要從事汽輪機加工工藝設計、質量管理工作。