一種煤礦事故分析與預(yù)測的新方法

陳學(xué)輝++李正貴

摘要：煤礦開采屬于特種作業(yè)，人的不安全行為和物的不安全狀態(tài)都可能引發(fā)事故的發(fā)生，容易造成重大人身傷害和財(cái)產(chǎn)損失。事故的分析和預(yù)測是安全的重要保證，針對事故樹頂上事件的發(fā)生概率對系統(tǒng)安全評價(jià)的重要性，首先介紹了集對分析的基本理論，以及集對分析理論與事故樹分析的結(jié)合求解頂上事件發(fā)生概率的模型；接著舉例加以說明，并分析計(jì)算結(jié)果；最后總結(jié)了運(yùn)用集對分析方法在對頂上事件發(fā)生概率進(jìn)行判定的優(yōu)越性。同以往的求解的方法相比，集對分析理論是從同一性、差異性和對立性三個(gè)方面對基本事件發(fā)生概率進(jìn)行預(yù)測，這樣更加的符合煤礦系統(tǒng)工程實(shí)際。

Abstract： Coal Mining is a special operation， the unsafe behavior or material insecurity is likely to cause accidents， leading to significant personal injury and property damage. Accident Analysis and forecasting is an important guarantee of security， for the importance of the fault tree top event's occurrence probability for systematic safety assessment， first， the theory of set pair analysis and the solution model that the theory of set pair analysis combines with fault tree analysis at the aspect of top event's occurrence probability are introduced. Next， some examples are taken to explain the method and the calculation result is analyzed. Last， the advantages of using set pair analysis to judge the top event's occurrence probability are summarized. Comparing with previous solutions， set pair analysis theory predicts the basic events' occurrence probability from 3 aspects： identity， difference， and opposition， which is more consistent with coal mine system engineering reality.

關(guān)鍵詞：煤礦開采；集對分析；頂上事件；事故樹

Key words： coal mining；set pair analysis；top event；fault tree

中圖分類號：X928 文獻(xiàn)標(biāo)識碼：A 文章編號：1006-4311（2017）21-0178-03

0 引言

我國是一個(gè)煤礦大國，煤礦開采過程中事故的發(fā)生屢見不鮮，每一次都是血淋淋的教訓(xùn)，分析和預(yù)防事故的發(fā)生已成為煤礦實(shí)際生產(chǎn)的重中之重。對事故的分析和預(yù)防的方法較多，定性分析、定量分析、定性與定量結(jié)合分析是目前最常用的三種方法。但上述三種方法，不同程度上存在主觀性強(qiáng)、簡單化、模糊化，因此普遍適應(yīng)性較差[1，2]。本文針對目前常用事故分析方法的局限性，引入集對分析理論，將該理論與事故樹分析相結(jié)合，提出一種新的分析方法。

1 集對分析的基本理論

1.1 集對分析的概念

集對（Set pair，SP），是指不確定性系統(tǒng)中的有一定聯(lián)系的兩個(gè)集合組成的對子，一般表示為H（A，B）。例如：上下、剛?cè)帷⑻搶?shí)、大小、勝負(fù)、高低、胖瘦、好壞等，以及作用力與反作用力、化合與分解、正電與負(fù)電、太陽與地球、物質(zhì)與能源，還有系統(tǒng)與環(huán)境、歷史與未來、教師與學(xué)生、領(lǐng)導(dǎo)與群眾、安全與不安全等等，無一例外地是成對地存在。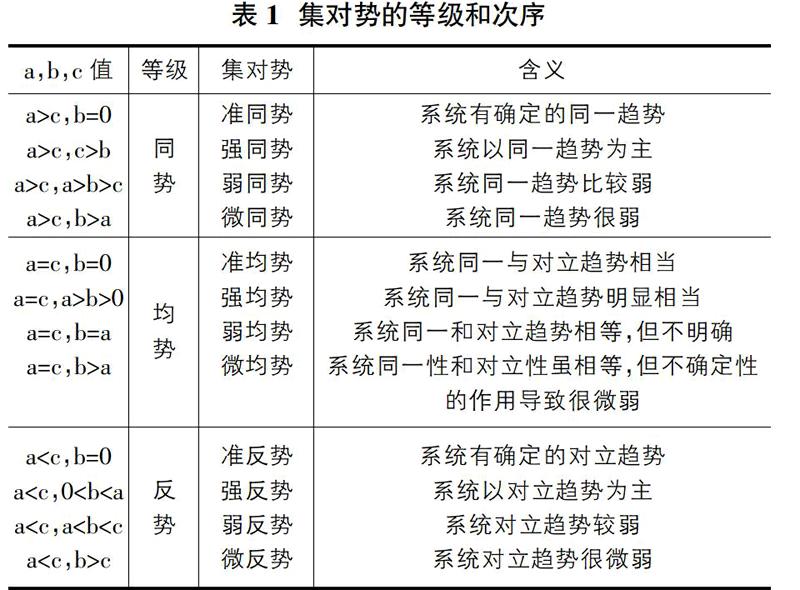

集對分析[3]（Set pair analysis，SPA），是指對不確定性系統(tǒng)中的兩個(gè)有關(guān)聯(lián)的集合構(gòu)造集對，對集對的某些特性做同一性、差異性、對立性分析，建立集對的同、異、反聯(lián)系度的分析方法。可見，SPA的基礎(chǔ)是集對，關(guān)鍵是聯(lián)系度的構(gòu)建和計(jì)算。

1.2 聯(lián)系度與聯(lián)系數(shù)

1.2.1 聯(lián)系度與聯(lián)系數(shù)的概念

事物是普遍聯(lián)系的，各類事物通常在某些特定屬性方面存在一定關(guān)系。三分原理，就是把這些關(guān)系的程度用三個(gè)明顯的特征來描述。集對分析方法，其核心思想是先對不確定性系統(tǒng)中的有關(guān)聯(lián)的兩個(gè)集合構(gòu)造集對，再對集對做某些特定屬性做同一性、差異性、對立性分析，然后用聯(lián)系度描述集對的同異反關(guān)系。設(shè)有聯(lián)系的集合X和Y，X和Y都有n項(xiàng)表示其特性，因此有X=（x1，x2，x3，…，xn），Y=（y1，y2，y3，…，yn）。表述H（X，Y）關(guān)系的聯(lián)系度的概念為[4]

式中：S表示同一性的個(gè)數(shù)；

F表示差異性的個(gè)數(shù)；

P表示對立性的個(gè)數(shù)；

S+F+P=n；

I表示不確定系數(shù)，在（-1，1）區(qū)間視不同情況取值，有時(shí)僅起差異標(biāo)記作用；

J表示對立系數(shù)，且J=-1，有時(shí)僅起對立標(biāo)記作用；

μX～Y表示集對H（X，Y）的聯(lián)系度。

令a=S/n，b=F/n，c=P/n，由式（1）可得

μX～Y=a+bI+cJ （2）

式中：a表示同一度；

b表示差異度；

c表示對立度；

a+b+c=1。

上式（2）中，a表示集合X和Y關(guān)于某種屬性具有相同性質(zhì)的程度；b表示集合X和Y關(guān)于某種屬性具有既不相同也不相反的性質(zhì)程度；c表示集合X和Y關(guān)于某種屬性具有相反性質(zhì)的程度。如果a越趨近于1時(shí)，表示這兩個(gè)集合的關(guān)系越趨近于同一；b越趨近于1時(shí)，表示這兩個(gè)集合的關(guān)系越趨近于差異；c越趨近于1時(shí)，表示這兩個(gè)集合的關(guān)系越趨近于對立。

當(dāng)I和J取合理值時(shí)，μX～Y變成一個(gè)數(shù)值，稱為這個(gè)數(shù)值為聯(lián)系數(shù)，記為μ'X～Y。根據(jù)聯(lián)系度的定義有：

-1≤μ'X～Y≤1。

1.2.2 聯(lián)系度與聯(lián)系數(shù)的意義

聯(lián)系度（μX～Y），通過a、b和c定量表征了不確定性系統(tǒng)中集合X和Y多層次上的關(guān)系，描述的系統(tǒng)是一個(gè)不確定性的系統(tǒng)；并能清晰地顯示關(guān)系的整體性和局部結(jié)構(gòu)，直觀定量地揭示復(fù)雜關(guān)系中的三種或多種秉性；它表征了綜合不確定性，同時(shí)也是是動(dòng)態(tài)的。

聯(lián)系數(shù)是表征集對H（X，Y）關(guān)系程度的一個(gè)綜合定量指標(biāo)。集合X和Y趨向于相同，則聯(lián)系數(shù)大；相反，集合X和Y趨向于相反，則聯(lián)系數(shù)小。當(dāng)μ'X～Y接近于1、0、-1時(shí)，分別表示這兩個(gè)集合在某特定屬性方面越傾向于同一、對立和差異。

1.2.3 集對勢

聯(lián)系度μX～Y=a+bi+cj中的c≠0時(shí)，同一度a與對立度c的比值a/c為集對勢。根據(jù)集對勢，可以得出系統(tǒng)安全狀態(tài)和發(fā)展趨勢。

2 聯(lián)系度的基本算法和應(yīng)用法則

2.1 聯(lián)系度的和積運(yùn)算法則[5-7]

2.1.1 聯(lián)系度的加法法則

設(shè)有μ1=a1+b1i+c1j，μ2=a2+b2i+c2j，兩個(gè)聯(lián)系度的加法有如下法則

μ1+μ2=a1+a2+（b1+b2）i+（c1+c2）j

=2[（a1+a2）/2+（b1+b2）i/2+（c1+c2）j/2]（3）

2.1.2 聯(lián)系度的乘法法則

根據(jù)聯(lián)系度乘法運(yùn)算法則，ij=i，i2=i，j2=1，因此兩個(gè)聯(lián)系度相乘如下：

μ1μ2=（a1+b1i+c1j）（a2+b2i+c2j）

=a1a2+a1b2i+a1c2j+a2b1i+b1b2i2+c2b1ij+a2c1j+c1b2ij+c1c2j2

=（a1a2+c1c2）+a1b2i+a2b1i+c2b1ij+c1b2ij+b1b2i2+（a1c2+a2c1）j

=（a1a2+c1c2）+（a1b2+a2b1+c2b1+c1b2+b1b2）i+（a1c2+a2c1）j（4）

在這里僅僅是列舉了兩個(gè)聯(lián)系度的和積算法，根據(jù)聯(lián)系度的算法規(guī)則，可以推廣到n個(gè)聯(lián)系度的和積形式。

2.2 集對分析與事故樹的融合

對于在事故樹方面運(yùn)用集對分析的基本原理，下面舉例說明集對分析在事故樹方面的運(yùn)用[8，9]。

假設(shè)對某一事故樹頂上事件發(fā)生概率進(jìn)行計(jì)算時(shí)，各基本事件為x1，x2，x3，…，xn，存在下面兩種情況：

3 集對分析法在事故樹分析中的運(yùn)用

如圖1所示為某次煤礦事故事故樹圖的簡化，各基本事件的聯(lián)系度系數(shù)如表2給出。運(yùn)用聯(lián)系度的方法計(jì)算頂上事件的聯(lián)系度（μX～Y）和聯(lián)系數(shù)（μ'X～Y）[10]。

①根據(jù)事故樹圖可得如下：

T=G3+G4

=X1G1+X2G2

=X1（X3+X4）+X2（X5+X6）

=X1X3+X1X4+X2X5+X2X6

從上式可以得出，事故樹有四個(gè)最小割集，分別為{X1，X3}，{X1，X4}，{X2，X5}，{X2，X6}。

②運(yùn)用上面提到的事故樹頂上事件聯(lián)系度的計(jì)算公式可得如下：

μT=μ1（μ3+μ4）+μ2（μ5+μ6）

=2（0.1+0.5i+0.4j）（0.1+0.75i+0.15j）

+2（0.1+0.4i+0.5j）（0.1+0.45i+0.45j）

=2（0.07+0.875i+0.055j）+2（0.235+0.67i+0.095j）

=4（0.1525+0.7725i+0.075j）

在式μT=4（0.1525+0.7725i+0.075j）中，式中系數(shù)4表示事故樹中最小割集的個(gè)數(shù)為4個(gè)，對μT分析，只需考慮μT″=0.1525+0.7725i+0.075j。由于聯(lián)系數(shù)-1≤μ'X～Y≤1，將μT″分為三個(gè)區(qū)間“危險(xiǎn)”[-1，-0.333]，“一般安全”[-0.333， 0.333] ，“安全”[0.333，1]。j作為對立面恒取j=-1。

對式μT″=0.1525+0.7725i+0.075j進(jìn)行分析：

①當(dāng) i=-1時(shí)，μT″=-0.695，系統(tǒng)安全等級為“危險(xiǎn)”；當(dāng)i=0時(shí)，μT″=0.145，系統(tǒng)安全等級為“一般安全”；當(dāng)i=1時(shí)，μT″=0.85，系統(tǒng)安全等級為“安全”。因此μT″的取值范圍為[-0.695，0.85]。μT″的下線為-0.695處于危險(xiǎn)當(dāng)中，必須引起重視，應(yīng)查找薄弱環(huán)節(jié)，及時(shí)整改加強(qiáng)安全管理水平，提高系統(tǒng)安全等級。

②根據(jù)集對勢對μT″進(jìn)行分析可知，b（0.7725）最大，系統(tǒng)處于“一般安全”中。根據(jù)表1，b>a>c，屬于微同勢，整體處于“臨界安全”狀態(tài)，但是系統(tǒng)同一勢很弱，也即“安全”趨勢很弱。因此，應(yīng)當(dāng)查找危險(xiǎn)源，規(guī)避風(fēng)險(xiǎn)。由于b較大，系統(tǒng)處于“臨界安全”的權(quán)重較大，而系統(tǒng)在運(yùn)行的過程總是處于“危險(xiǎn)”、“一般安全”和“安全”三個(gè)等級中循環(huán)，因此由“一般安全”狀態(tài)轉(zhuǎn)向“危險(xiǎn)”狀態(tài)概率也增大。在定期的安全檢查中，對于系統(tǒng)處于“一般安全”等級中，應(yīng)當(dāng)引起足夠的重視，防止其向“危險(xiǎn)”狀態(tài)轉(zhuǎn)移。

4 結(jié)論

①本文引用同一性、差異性、對立性三個(gè)方面概率替代單一頂上事件發(fā)生概率，并針對系統(tǒng)安全狀態(tài)運(yùn)用集對分析的基本原理和方法進(jìn)行分析，改變了傳統(tǒng)方法對事故分析的單一性和局限性。

②為了最大程度地降低頂上事件發(fā)生概率，本文一方面考慮了在最小割集或徑集中出現(xiàn)頻率較高的事件；另一方面運(yùn)用集對分析理論，并進(jìn)行舉例論證，提出了降低“差異性事件”發(fā)生概率的方法。

③根據(jù)集對分析的基本原理，可對單一差異性進(jìn)行替換，即將bi替換為b1i1+b2i2+b3i3+…+bnin。以此進(jìn)行計(jì)算和分析，提高了差異性的維度，可以得到更加精準(zhǔn)的結(jié)果。

參考文獻(xiàn)：

[1]徐志勝.安全系統(tǒng)工程[M].北京：機(jī)械工業(yè)出版社，2007.

[2]崔國章，張景林.安全系統(tǒng)工程[M].北京：煤炭工業(yè)出版社， 2002.

[3]趙克勤.集對分析及其初步運(yùn)用[M].杭州：浙江科技出版社，2000.

[4]王文圣，李躍清，金菊良等.水文水資源集對分析[M].北京：科學(xué)出版社，2010.

[5]趙克勤，米紅.非傳統(tǒng)安全與集對分析[M].北京：知識產(chǎn)權(quán)出版社，2010.

[6]趙克勤.集對分析的不確定性系統(tǒng)理論在AI中的應(yīng)用[J].智能系統(tǒng)學(xué)報(bào)，2006，1（2）：16-25.

[7]劉秀梅，趙克勤.基于集對分析聯(lián)系數(shù)的信息不完全直覺模糊多屬性決策[J].數(shù)學(xué)的實(shí)踐與認(rèn)識，2010，40（1）：67-77.

[8]黃大榮，黃麗芬.基于集對分析聯(lián)系數(shù)故障樹的BA系統(tǒng)可靠性分析[J].計(jì)算機(jī)應(yīng)用研究，2010，27（1）：111-113.

[9]廖文來，何金平.基于集對分析的大壩安全綜合評價(jià)方法研究[J].人民長江，2006，37（6）：57-58，61.

[10]鄭欣，許開立，周家紅.基于集對分析的尾礦庫安全評價(jià)研究[J].安全與環(huán)境學(xué)報(bào)，2008，8（1）：160-162.