CCPAZP-FFT捕獲方法中頻率估計算法研究

唐振剛,徐云東,李曉敏,王 瑞,謝寶蓉

(1.上海衛星工程研究所,上海 201109; 2.上海電子技術研究所,上海 201109; 3.北京理工大學 信息與電子學院,北京 100081)

?

CCPAZP-FFT捕獲方法中頻率估計算法研究

唐振剛1,徐云東1,李曉敏2,王 瑞3,謝寶蓉2

(1.上海衛星工程研究所,上海 201109; 2.上海電子技術研究所,上海 201109; 3.北京理工大學 信息與電子學院,北京 100081)

針對航天測控系統中因飛行器高速運動造成的直擴信號多普勒頻率捕獲精度下降問題，對CCPAZP-FFT捕獲方法中的頻率估計算法進行了研究。結合M-Rife頻率估計方法，通過頻譜搬移將原始信號真實頻率移動至量化頻率中心，對獲得的頻譜的最大值與次大值進行插值，同時對捕獲峰值的相鄰相位維進行多普勒修正，提高多普勒頻率的捕獲精度。給出了算法的步驟，以及基于K7芯片的現場可編程邏輯陣列(FPGA)的實現流程。理論分析和仿真結果驗證了算法的有效性，在接收信號載噪比38 dB、多普勒動態-70～70 kHz的環境中，多普勒捕獲偏差由250 Hz降至約10 Hz，實測結果驗證了算法的可行性。

測控系統； 高動態； 直擴信號； 捕獲； 多普勒精度； 頻率估計； 相位修正； CCPAZP-FFT算法； M-Rife算法

0 引言

隨著航天技術的進展，航天測控向深空探測及更高頻段測控發展[1]。由于飛行器與地面測控站相距甚遠，徑向飛行速度快且加速度大，使測控信號具備了高動態特性。高動態環境中，直擴信號的偽碼、數據位也隨運動造成相位的動態變化，這樣在與本地再生信號相關的過程中，將增大相關誤差，降低多普勒、偽碼的估計精度。針對該問題，可通過縮小頻域搜索間隔但增加捕獲時間解決[2]。文獻[3]在縮小搜索步進的基礎上對校正進行了研究以縮小捕獲時間；文獻[4]通過補零增加快速傅里葉變換(FFT)處理點數以減小搜索間隔。這些方法大多增加了相干運算資源或時間，一定程度減弱了多普勒頻率對偽碼相位的搜索的影響。通過提高多普勒頻率的估計精度，進而可改善偽碼相位的捕獲精度。目前，在針對頻率估計提出的算法中，基于頻域插值的頻率估計算法因實現結構簡單且運算復雜度低，在工程中應用廣泛。基于頻域插值的頻率估計法主要包括Rife算法、Quinn算法、M-Rife算法等，其中M-Rife算法的估計精度較高[5-7]。

在高動態環境中，為減弱相關時間內偽碼走動導致的相關性能下降的影響，常用的捕獲方法是將時間維或頻率維并行，如常用的多普勒串行偽碼并行捕獲算法是基于FFT的偽碼并行相關捕獲，常用的多普勒并行偽碼串行捕獲算法是PMF-FFT算法[8-9]。CCPAZP-FFT捕獲方法則將時、頻二維同時并行，算法基于分段補零循環相關，通過分段補零的方法并結合FFT循環相關運算，將超長序列的相關運算轉換為一系列子序列的線性運算，并通過FFT鑒頻將二維搜索過程轉化為一維的并行搜索，顯著縮短了捕獲時間。CCPAZP-FFT算法的多普勒捕獲精度受限于選取的相關時間長度，但在高動態環境中延長相關處理時間不僅會降低相關性能，而且會增大捕獲時間。針對此問題，基于大動態應用背景，由二維并行的CCPAZP-FFT捕獲方法，結合M-Rife算法，利用CCPAZP-FFT獨特的偽碼相位維信息，本文對CCPAZP-FFT捕獲方法中的頻率估計算法進行了研究，以實現高動態環境中的多普勒精確估計，另外對算法性能進行了Matlab仿真驗證以及FPGA實測分析。

1 算法原理

對一個單載波信號作FFT變換，根據頻域出現的峰值位置k可推算出信號的頻率f0=k×fs/N。此處：fs為采樣頻率；N為采樣點數。因對時域信號采樣后的取點處理會造成頻譜泄露，同時FFT頻率分辨率有限，故當目標信號的多普勒頻率不是頻率分辨率的整數倍時，會出現信號經FFT處理后的峰值位于頻域兩采樣點間，造成較大的頻率估計誤差。對此問題，提出了提高檢測精度的頻率估計算法。其中：M-Rife算法是基于Rife算法的改進算法，通過對信號的預處理，可避免出現信號實際多普勒靠近離散頻點時出現插值方向錯誤的問題。

M-Rife算法的實現方式為：先取峰值位置處的頻域點坐標k0，令k0對應幅值為|X(k0)|，同時選取峰值兩側譜線幅值|X(k0-1)|，|X(k0+1)|中的最大值|X(k1)|作為頻域次峰值(k1為|X(k1)|對應位置的頻域坐標)，根據主次峰值的比值關系可得信號實際多普勒與頻率估計值間的差值

(1)

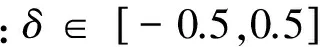
(2)

(3)

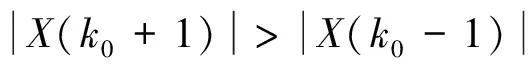
(4)

處理。再對x′(n)信號重新進行頻率估計，將新估得的多普勒疊加上頻移處理的多普勒，從而獲得準確的多普勒值。

M-Rife算法通過頻移處理，避免信號落入偏差較大的區域，運算量增加相對Rife算法并不多，但能較好地解決Rife算法插值方向錯誤的問題，算法估計出的多普勒可信度高，因此本文將其作為頻率估計的基本算法。

本文的CCPAZP-FFT捕獲方法中的頻率估計算法原理如圖1所示[7]。算法的處理步驟如下。

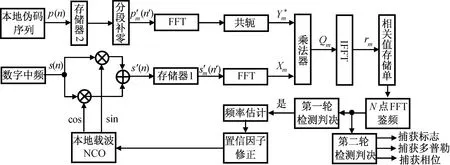
圖1 CCPAZP-FFT捕獲算法原理Fig.1 Principle of CCPAZP-FFT algorithm

a)接收機接收數字中頻信號s(n)，本地載波NCO先根據粗搜多普勒步進對信號進行下變頻處理，得到復數形式的信號s′(n)，將接收信號采樣存入存儲器1。與此同時，對本地偽碼進行采樣并存入存儲器2。

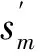
(5)

式中：

此處：A為接收信號s(n)的幅值；τ為接收序列與本地偽碼序列的相位差；fd為目標信號多普勒；

合并M組相關結果向量rm，得到一個X×M維矩陣，表示搜索完X個相位差的相關結果存儲結果。其中：矩陣的每列是長為2X的本地碼序列和接收碼序列作FFT-IFFT前X項的相關結果；矩陣的每行對應同一相位差的相關結果。

d)將相關處理后的矩陣按行送入FFT頻差搜索單元，對同一搜索相位差的存儲單元中的M個相關值進行FFT運算，并對FFT結果取模，得到FFT鑒頻輸出第k點輸出歸一化頻率響應

GPMF-FFT(k,fd)=

(6)

式中：

e)為提高信號的檢測能量，重復步驟a)～b)P次，將每次鑒頻得到的相關模值進行累加，得到P次非相參累加結果，至此完成X個相位差的搜索。

f)重復步驟a)～e)M次，完成整個偽碼不確定區間的區間搜索，即完成M×X個本地偽碼與接收信號的相位差的相關運算。

g)對所有相位的非相參累積結果進行選大，取出最大值所在相位維的所有結果，即對應矩陣的某一行，根據該相位差的FFT鑒頻結果計算檢測判決量，若滿足判決條件，則取出矩陣中該相位差前后各一行的相關結果進行頻率估計的運算。

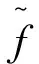
(7)

式中：ki為某一相位維鑒頻結果對應的峰值坐標；δi為實際多普勒頻率與鑒頻多普勒頻率間的誤差量；i=1，2，3。

i)引入不同相位差頻率估計結果的權重因子αi，按不同的權重因子對不同相位差的多普勒估值進行加權，得到修正的最終估計多普勒

(8)

式中：fNCO為當前搜索的載波NCO的頻率。

j)將獲得的捕獲偽碼相位和多普勒頻率置入本地搜索單元，對信號進行第二輪捕獲，輸出捕獲結果。至此，完成高動態時提高捕獲多普勒精度處理。

2 算法的FPGA實現

算法的FPGA實現主要由CCPAZP-FFT捕獲模塊、M-Rife頻率估計及校正模塊，以及邏輯控制模塊組成，處理流程如圖2所示。

CCPAZP-FFT捕獲模塊首先將經60 MHz系統時鐘采用后的1 ms中頻正交數據內插為32 768點，考慮FFT鑒頻范圍和相關損失等性能，取部分相關點數為512點，FFT鑒頻點數為64點。將本地偽碼補零至1 024點，用FFT-IFFT運算實現512點的圓周相關運算，并將64段512點的相關結果存入ROM，再通過控制讀ROM的地址讀出同一相位的64點相關結果并輸入FFT鑒頻模塊，存儲鑒頻結果，由此完成512點的相位不確定區間的捕獲搜索。順序取下一段1 ms數據進行內插、部分相關、FFT鑒頻和結果存儲處理，直至完成所有相位不確定區間的搜索，對存儲的FFT鑒頻結果進行選大處理。若當前未檢測到Flow1_control，Flow2_control，則將第一輪捕獲標志Acq_flow1_flag，峰值所在位置對應的相位維鑒頻結果以及相鄰相位維的鑒頻結果FFT_freq_data輸出至M-Rife頻率估計與校正模塊；若檢測到Flow1_control，同樣將Acq_flow1_flag，FFT_freq_data輸出至M-Rife頻率估計與校正模塊；若檢測到Flow2_control，則將峰值對應的相位結果Acqcodephase、捕獲多普勒Acqdoppler，以及捕獲標志AcqFlag輸出至頂層，轉入跟蹤處理單元。

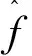
邏輯控制模塊檢測到Controlstart_en后需要對M-Rife頻率估計與校正模塊的最終估計頻率doppler_estimate進行判決。若滿足式(3)，則邏輯控制模塊輸出Flow1_control至CCPAZP-FFT捕獲模塊在doppler_estimate頻點處進行第二輪捕獲；否則，邏輯控制模塊輸出Flow2_control控制CCPAZP-FFT捕獲模塊對輸入信號以delta_k進行頻域移位處理，重新進行一輪捕獲及頻率估計處理。

基于Xilinx公司的K7 XC7K480T FPGA芯片，分別對本文的捕獲算法和無頻率估計的CCPAZP-FFT算法進行實現，兩種算法占用資源見表1。在算法的FPGA設計和實現過程中，根據自上而下的原則進行算法模塊劃分、兼顧實現資源與效率，算法實現平衡了頻率捕獲精度和消耗資源及復雜度間的矛盾。本文的CCPAZP-FFT捕獲方法中的頻率估計算法相對無頻率估計的CCPAZP-FFT算法只增加了約4%的Slice資源。

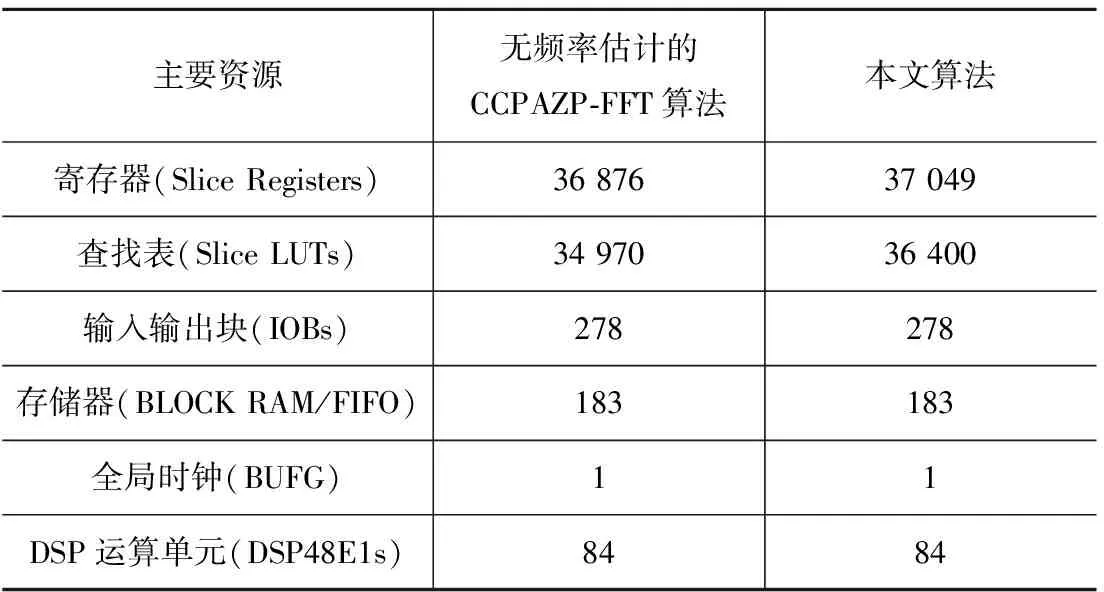
表1 FPGA資源占用

圖2 算法FPGA處理流程Fig.2 FPGA process flowchart of algorithm

3 仿真及實測驗證

3.1 仿真驗證

在接收信號載噪比38 dB，多普勒動態范圍-70～70 kHz的環境中，設仿真參數：偽碼為Gold碼，速率10.23 MHz，碼長10 230；相干積分時間1 ms；射頻頻率2 GHz；采樣頻率60 MHz，對算法性能進行仿真驗證，比較無多普勒估計與采用M-Rife的CCPAZP-FFT算法的捕獲多普勒偏差。為減少噪聲影響，對每個頻點的100次捕獲多普勒結果進行均方根運算統計誤差，仿真結果如圖3所示。

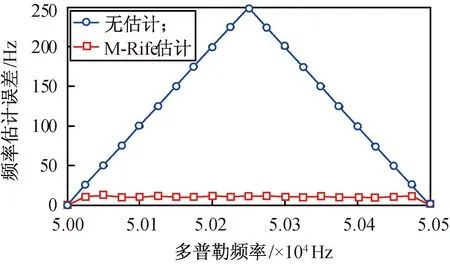
圖3 有無頻率估計時捕獲多普勒偏差Fig.3 Doppler frequency difference with frequency estimation or not

根據仿真參數設置可知：CCPAZP-FFT鑒頻的頻率分辨率500 Hz，當目標多普勒在50.0～50.5 kHz范圍內變化時，捕獲的頻點為50.0 kHz或50.5 kHz，因此在不對捕獲結果進行頻率估計時，最大捕獲頻率偏差為250 Hz；在捕獲中采用M-Rife估計后，捕獲多普勒偏差基本不隨目標頻點而變，且誤差范圍遠小于250 Hz。引入相鄰相位維修正和無修正的捕獲多普勒誤差結果如圖4所示。由圖4可知：將峰值相鄰相位維的多普勒估計結果與峰值對應的估計結果進行不同權重累加后，可一定程度提高多普勒捕獲的精度，減小相位不對齊時的頻率估計誤差。

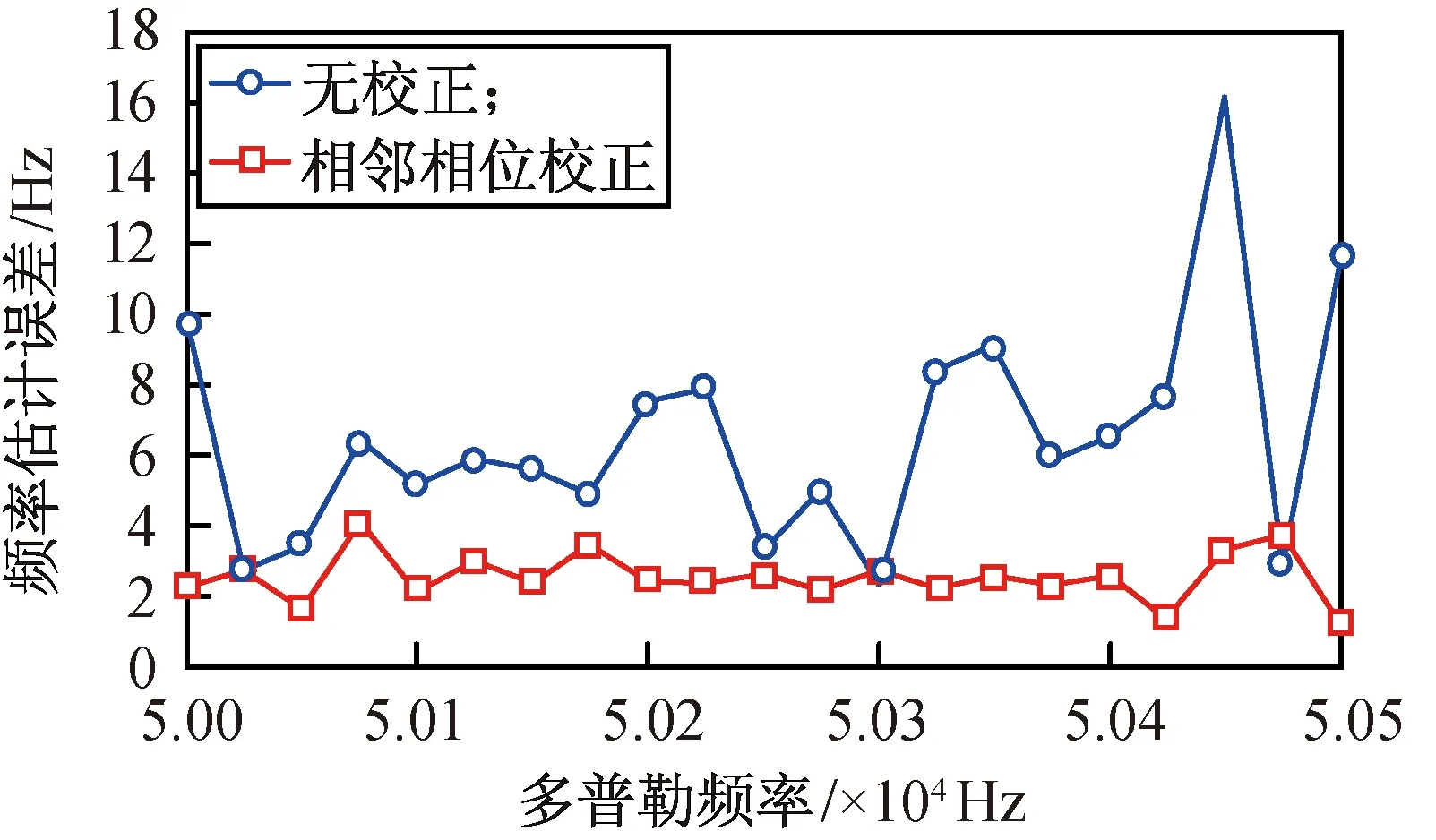
圖4 有無引入相位修正時捕獲多普勒偏差Fig.4 Doppler frequency difference with phase correction or not

3.2 實測驗證

在不同載噪比下對基于FPGA實現的算法進行捕獲性能測試。由于算法鑒頻的頻率分辨率為500 Hz，為驗證M-Rife頻率估計算法對捕獲多普勒精度的改善作用，將目標多普勒設置在兩量化頻率的中間位置，則實測時設置的信號源多普勒為50.25 kHz，且在每個目標頻點均進行100次測試。載噪比由35 dBHz下降至31 dBHz，目標多普勒為50.25 kHz時改進算法和常規算法的捕獲概率、捕獲多普勒均方根誤差見表2。

由表2可知：在低載噪比環境中，改進算法的捕獲概率高于常規算法，且隨載噪比的降低，改進算法的頻率捕獲誤差變化緩慢，遠小于常規算法的捕獲多普勒誤差250 Hz。實測結果與Matlab仿真結果一致，表明算法可行。

4 結束語

本文對高動態環境中因捕獲時間增長，捕獲相關性能減弱等因素導致的捕獲多普勒精度下降問題進行了研究。選取時、頻二維并行捕獲的CCPAZP-FFT算法作為捕獲算法，研究了CCPAZP-FFT捕獲方法中的頻率估計算法，算法通過對鑒頻結果進行M-Rife估計，引入相位維信息對估計多普勒進行修正，得到精度較高的頻率估值，并根據修正后的結果進行二次捕獲，提高捕獲多普勒精度。本文闡述了算法的設計思路、算法流程，分析了算法性能，并對算法性能進行仿真驗證。理論分析、仿真結果和實測結果均表明：在占用資源基本不變的前提下，算法相對常規CCPAZP-FFT捕獲算法，提高了捕獲多普勒精度。后續可研究算法對復雜環境的適應能力，如單音干擾、異址干擾及多徑干擾等環境。

表2 改進算法與常規算法實測性能

[1] 張碧雄, 巨蘭. 2030年前航天測控技術發展研究[J]. 飛行器測控學報, 2010, 29(5): 11-15.

[2] 楊小江, 毛峽, 王鵬飛. 基于FPGA的高動態GPS信號FFT快捕設計與實現[J]. 西安電子科技大學學報, 2007, 34(6): 170-172.

[3] 張兆維, 李文剛, 周彥果, 等. 高動態接收機的多普勒頻偏捕獲新算法[J]. 西安電子科技大學學報, 2015, 42(2): 7-12+51.

[4] 段瑞楓, 劉榮科, 周游, 等. 一種低復雜度的極低信噪比高動態信號載波粗捕獲算法[J]. 航空學報,

2013, 34(3): 662-669.

[5] IGLESIAS V, GRAJAL J, SANCHEZ M, et al. Implementation of a real-time spectrum analyzer on FPGA platforms[J]. IEEE Transactions on Instrumentation & Measurement, 2015, 64(2): 338-355.

[6] SO H C, CHAN F K W. A generalized weighted linear predictor frequency estimation approach for a complex sinusoid[J]. IEEE Transactions on Signal Processing, 2006, 54(4): 1304-1315.

[7] BORKOWSKI J, KANIA D. Interpolated-DFT-based fast and accurate amplitude and phase estimation for the control of power[J]. Metrology and Measurement Systems, 2016, 23(1): 13-26.

[8] Van NEE D J R, COENEN A J R M. New fast GPS code-acquisition technique using FFT[J]. Electronics Letters, 1991, 27(2): 158-160.

[9] CHENG J, ZHU W, LI G. A fast non-data aided PN code acquisition method based on FFT[C]// International Symposium on Communications and Information Technologies. Bangkok, [s. n.], 2006: 395-398.

Research of Frequency Estimation Algorithm in CCPAZP-FFT Acquisition Technology

TANG Zhen-gang1, XU Yun-dong1, LI Xiao-min2, WANG Rui3, XIE Bao-rong2

(1. Shanghai Institute of Satellite Engineering, Shanghai 201109, China; 2. Shanghai Aerospace Electronic Technology Institute, Shanghai 201109, China; 3. School of Information and Electronics,Beijing Institute of Technology, Beijing 100081, China)

Aiming at acquisition Doppler precision declining problem of DSSS signal in TT & C system caused by high speed motion of spacecraft, a frequency estimation algorithm in CCPAZP-FFT acquisition was studied in this paper. The original true frequency was shifted to the quantify center frequency by M-Rife frequency estimation algorithm. The spectrum was obtained as the maximum value and high values were interpolated. Meanwhile, the adjacent phase dimension of the peak was modified by Doppler, which improved Doppler frequency acquisition accuracy. The algorithm principle and the flowchart realized by K7 FPGA chip were given out. Theoretical analysis and simulation results verified the effectiveness of the proposed algorithm. Under the environment of the received signal carrier noise ratio 38 dB and Doppler dynamic -70 ～ +70 kHz, the acquisition deviation from 250 Hz was reduced to about 10 Hz. The experimental results also verified the feasibility of the algorithm.

TT&C system; high dynamic; DSSS signal; acquisition; Doppler accuracy; frequency estimation; phase correction; CCPAZP-FFT algorithm; M-Rife algorithm

1006-1630(2017)03-0102-06

2016-08-14；

2016-10-16

國家自然科學基金資助(616505110)

唐振剛(1980—)，男，高級工程師，主要從事衛星總體研制。

TN92

A

10.19328/j.cnki.1006-1630.2017.03.014