一種基于改進形狀分析的黏滯特性檢測方法研究

孔杰，田學民，尚林源

(中國石油大學(華東) 信息與控制工程學院，山東 青島 266580)

一種基于改進形狀分析的黏滯特性檢測方法研究

孔杰，田學民，尚林源

(中國石油大學(華東) 信息與控制工程學院，山東 青島 266580)

調節閥黏滯特性是導致工業過程中控制回路振蕩的主要原因之一。現有的調節閥黏滯特性檢測方法大多都以特定假設為前提，只適用于特定的范圍。針對面積峰值法僅適用于自衡對象的限制，提出了一種改進的形狀分析法，基于自衡對象和積分對象回路輸出形狀的差異，對振蕩回路偏差信號的二階導數信號與原信號的較大差異性進行區分，從而進行黏滯特性檢測。該方法克服了面積峰值法只適用于特定范圍的局限性，通過仿真研究驗證了該方法的有效性。

黏滯特性 振蕩診斷 調節閥 非線性特性

回路振蕩是過程工業中常見的現象，據統計約33%的控制回路處于振蕩狀態中[1]，該現象會直接導致控制性能變差、產品質量降低、能源的損耗增大等問題產生[2]。

引起控制回路產生振蕩現象的原因主要包括： 控制器參數整定不當、閥門黏滯和外部周期性干擾[3]。研究表明[4]： 有20%～30%的回路振蕩是由調節閥引起的，調節閥死區、飽和以及黏滯等非線性特性都會不同程度地影響控制回路性能，其中尤以調節閥黏滯特性最為常見。因此，研究調節閥黏滯特性，對石油化工等工業過程安全、穩定、高效的生產有著非常重要的意義。

近年來，關于調節閥黏滯特性檢測的研究成果不斷涌現，Capaci和Scali[5]對黏滯特性檢測方法進行了綜述。張波[6]將這些方法分為四大類： 基于互相關函數法，基于形狀分析法，基于非線性檢測法以及基于模型的算法[7-10]。基于形狀分析算法主要包括基于OP-MV形狀分析法[11-12]、面積峰值法[13]和曲線擬合法[14-15]；基于非線性檢測算法主要有雙相干法[16]和替代數據分析法[17]。

Horch[18]提出了利用控制器輸出信號與過程輸出信號的互相關函數的奇偶性來判斷黏滯存在情況，但此方法僅適用于PI控制器下的非積分過程。Rossi&Scali[14]提出了曲線擬合法，通過擬合回路中第一個積分環節后的變量信號，分別比較與正弦信號和三角信號的擬合度，判斷是否存在調節閥黏滯特性。雙相干方法對信號中非穩態緩慢變化的趨勢非常敏感，需要進行維納濾波；替代數據分析法[17]至少需要12個周期數據并且對非末端匹配數據非常敏感，原則上結合橢圓擬合法也可用于黏滯檢測。Daneshwar和Noh[19]提出了基于模糊聚類的方法進行黏滯特性檢測，僅應用于流量控制系統。基于OP-MV形狀分析法[11-12]是利用控制器輸出OP和閥門輸出MV之間的關系所繪制二維圖的形狀來判斷黏滯特性，該類方法容易理解、執行簡單，但需要得到閥門輸出MV信號，應用范圍受到限制。面積峰值法通過計算回路偏差信號過零點間峰值前后的面積比值來判斷回路中是否存在黏滯特性，該方法需要對過零點和峰值檢測，只適用于自衡對象。

目前，調節閥黏滯檢測方法比較多，通常都是以特定的假設為前提，因而只適用于特定的范圍。針對面積峰值法僅適用于自衡對象的限制，筆者對其進行了改進，使其可適用于自衡對象和積分對象，同時能夠更高效地進行黏滯特性檢測，通過仿真研究驗證了該方法的有效性。

1 調節閥黏滯特性

調節閥常見的非線性特性主要有死區、飽和、黏滯等，其中黏滯特性又最為常見，如圖1所示，圖中OP是控制器輸出信號，MV是調節閥輸出信號，S表示死區(AB段)加黏性區(BC段)參數，J表示滑動跳躍(CD段)參數。

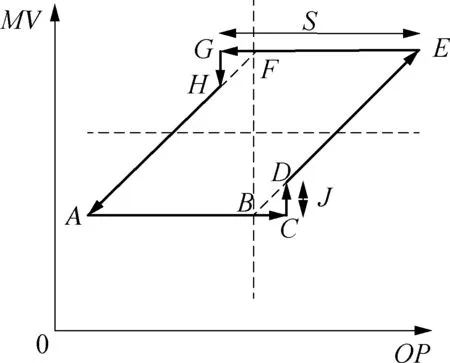
圖1 典型閥門黏滯特性示意

圖1中，當閥門黏滯引起回路振蕩時，黏性閥門的運動可以明確地劃分為四個階段： 死區階段(AB段)，黏性階段(BC段)，滑動跳躍階段(CD段)和連續運動階段(DE段)。

假設閥門初始位于A點，同時閉環回路穩定運行，由于負載擾動的存在，使得回路產生控制偏差時，控制器輸出OP開始增加。如果OP信號不在閥門能夠響應的輸入范圍之內，閥門由A點進入死區階段，MV不會隨著OP的增大而運動，也不會積累勢能。OP信號繼續增大，并在B點進入有效輸入范圍之內，此時閥門由死區階段過渡到黏性階段，閥門能夠感覺到OP的控制作用，但由于OP所產生的作用力小于靜摩擦力，閥門無法對控制作用做出響應，因而雖然會積累勢能，但仍然會保持靜止狀態。當到達C點時，OP產生的作用力超過了靜摩擦力，閥門進入滑動跳躍階段，閥門位置突然變化。由D到E是閥門的連續運動階段，此時閥門位置會隨著OP的增大而連續滑動，產生控制作用，減小控制偏差。當偏差減小到一定程度，OP開始減小，此時閥門試圖反向運動，但這種運動趨勢再次被摩擦力阻止，閥門由E點再次進入黏性階段，并重復上述的運動過程，最終回路發生振蕩。

2 基于改進形狀分析的黏滯特性檢測方法

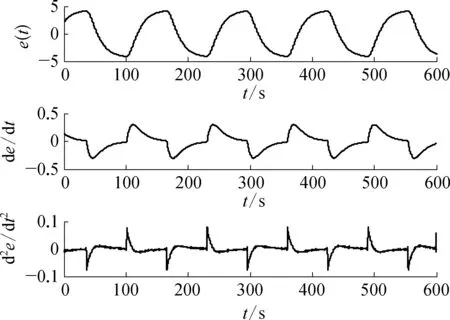
研究表明： 不同原因導致的控制回路振蕩，過程輸出的偏差信號也不同。在調節閥黏滯特性的作用下，自衡對象的偏差信號表現為近似方波信號，如圖2所示；對于有積分作用的非自衡對象，偏差信號表現為三角波信號，如圖3所示；由控制器參數整定不當導致的振蕩，偏差信號表現為正弦波信號，如圖4所示。

對于自衡對象，有黏滯特性的控制回路波形具有不對稱性，如圖2所示，文獻[13]針對這個性質提出了峰值前后面積比較的指標R：

(1)

式中：A1——峰值與峰值前過零點之間的曲線與橫軸圍成的面積；A2——峰值與峰值后過零點之間的曲線與橫軸圍成的面積，通過R的大小來判斷是否存在黏滯特性。如果比值大于1則表明控制回路波形不對稱即回路中存在黏滯特性；如果約等于1表明不存在黏滯特性。判斷規則如下，記為規則一：

(2)

式中：δ——閾值，它的大小取決于黏滯特性檢測方法的靈敏性。δ值越小，對檢測方法靈敏性要求越高，同時判斷結果的準確率也會降低；反之，δ值越大，則對檢測方法靈敏性要求越低，判斷結果的準確率會增加。為了更好地權衡兩者之間的關系，δ的值通常取0.5～1.0[13]。

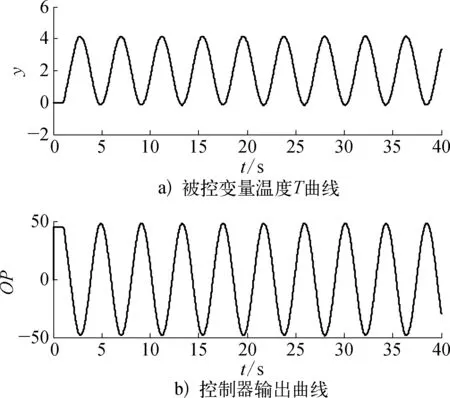
由于調節閥黏滯特性參數取值的不同，回路波形的不對稱性包括A1>A2和A1

(3)

然而，由圖3和圖4可知，對于積分對象中的黏滯特性所導致的三角波信號和控制器參數整定不良導致的正弦信號，在采用式(3)的判斷規則進行判斷時均可能會得到R≈1的結果，即不能正確地檢測到相應的黏滯特性和控制器參數整定不當。為解決上述問題，利用正弦信號與三角波信號二階求導后所得信號的較大差異性進行檢測判斷，如圖5所示。正弦信號經二次求導后成為相角發生偏移的正弦信號；而三角波信號經二次求導后成為正負交替的脈沖信號。基于此差異做進一步的檢測。

由于周期信號求導后的幅值與原信號幅值成一定倍數關系，比值為角頻率，因而提出基于二階求導信號與原信號在1個振蕩周期內面積比值的指標：

(4)

式中：As0——振蕩回路偏差信號幅值歸一化后所得信號在1個周期內與橫軸圍成的面積；As2——振蕩回路偏差信號經過二階求導后所得信號在1個周期內與橫軸圍成的面積。通過以上分析可知，如果Rs約等于0表明控制回路振蕩信號近似為三角波信號，即調節閥存在黏滯作用；如果Rs約等于1表明回路振蕩是由控制器參數整定不當所致，調節閥不存在黏滯作用。

因此對規則二進一步完善如下：

(5)

考慮到實際過程數據通常受到噪聲干擾，且噪聲信號的導數對指標影響較大，為易于工程應用，需要將各階導數信號進行濾波且將上述規則描述如下，記為規則三：

(6)

圖2 自衡對象存在黏滯特性時的偏差信號示意

圖3 積分對象存在黏滯特性時的偏差信號示意

圖4 控制器參數整定不當導致的偏差信號示意

圖5 不同波形信號的二階導數信號示意

其中檢測閾值尚沒有理論方法確定，往往只能通過反復試驗的方式確定。由上面分析可以知道，改進的面積比值法可以適用于自衡對象和積分對象，克服了文獻[13]的使用范圍的局限性。下面的仿真實驗驗證了該方法的有效性。

3 仿真實驗

3.1 自衡對象仿真研究

以某典型工業加熱爐為仿真對象，其結構如圖6所示，假設進料F恒定，通過調整燃料U來保證出口溫度T恒定，建立模型如下：

采用PID控制器對加熱爐回路進行控制，將進料值設置為F=1，設定值r=2，且控制回路運行良好時PID控制器參數為KP=0.11,KI=

0.008 5,KD=0，設置信噪比為70的高斯白噪聲，分別在存在黏滯特性以及控制器參數整定不當的情形下進行仿真研究。

圖6 典型工業加熱爐結構示意

1) 調節閥存在黏滯特性時的情況。設置不同的調節閥黏滯參數使得回路發生振蕩，當S=0.4,J=0.5時，圖7為調節閥存在黏滯特性時的特性曲線，圖8a)為被控變量溫度T的曲線圖，圖8b)為控制器輸出曲線圖，圖9為濾波后偏差的各階導數數據，計算2個指標R和Rs進而判斷引起回路振蕩的原因，不同仿真參數下的指標結果見表1所列。

圖7 自衡對象黏滯特性存在時閥門特性曲線示意

圖8 自衡對象黏滯特性存在時回路數據示意

圖9 自衡對象黏滯特性存在時 偏差各階導數的數據示意

2) 控制器參數整定不當時的情況。將控制器參數設置為KP=0.817 5,KI=0.008 5,KD=0，此時回路發生振蕩，圖10為回路在控制器參數整定不當時調節閥的特性曲線，圖11a)為被控變量溫度T的曲線圖，圖11b)為控制器輸出曲線圖，圖12為濾波后偏差的各階導數數據，計算2個指標R和Rs進而判斷引起回路振蕩的原因，所得指標結果見表1所列。

圖10 自衡對象控制器參數整定不當時 閥門特性曲線示意

圖11 自衡對象控制器參數整定不當時 回路數據示意

圖12 自衡對象控制器參數整定不當時 偏差各階導數數據示意

工作情況SJRRs是否黏滯參數整定不當0 0 1.08421.0107否黏滯作用1.30.55.76990.1249是1.70.57.69610.1106是1.71.03.44450.1757是

通過表1得到的仿真結果，可以判斷出第1組數據所對應的回路振蕩是由控制器參數整定不當導致，而后3組數據所對應的回路振蕩是由閥門黏滯特性引起，結論與振蕩源的設置一致。

3.2 一階積分對象仿真研究

考慮單回路控制，控制對象采用文獻[20]中的一階積分仿真對象，其傳遞函數為

采用PID控制器對回路進行控制，設定值r=2，且控制回路運行良好時PID控制器參數為KP=7,KI=0,KD=0，設置信噪比為50的高斯白噪聲，分別在存在黏滯特性以及控制器參數整定不當情形下進行仿真研究。

1) 調節閥存在黏滯特性時的情況。設置不同的調節閥黏滯參數使得回路發生振蕩，當S=2.3,J=1時，圖13為調節閥存在黏滯特性時的特性曲線，圖14a)為被控變量溫度T曲線，圖14b)為控制器輸出曲線回路數據，圖15為濾波后偏差的各階導數數據，計算2個指標R和Rs進而判斷引起回路振蕩的原因，不同仿真參數下的指標結果見表2所列。

2) 控制器參數整定不當時的情況。將控制器參數設置為KP=22.44,KI=0,KD=0，此時，回路發生振蕩，圖16為回路在控制器參數整定不當時調節閥的特性曲線，圖17a)為被控變量溫度T曲線，圖17b)為控制器輸出曲線回路數據，圖18為濾波后偏差的各階導數數據，計算2個指標R和Rs進而判斷引起回路振蕩的原因，所得指標結果見表2所列。

圖13 積分對象黏滯特性存在時閥門特性曲線示意

圖14 積分對象黏滯特性存在時回路數據示意

圖15 積分對象黏滯特性存在時偏差 各階導數數據示意

圖16 積分對象控制器參數整定不當時 閥門特性曲線示意

圖17 積分對象控制器參數整定 不當時回路數據示意

圖18 積分對象控制器參數不當時 偏差各階導數數據示意

工作情況組數SJR是否黏滯(規則一)是否黏滯(規則二)Rs是否黏滯(規則三)參數整定不當10 0 1.0258否否0.9998否黏滯作用22.70.33.2177是是0.1978是33.60.31.3994待定待定0.1593是44.30.30.9839待定待定0.1245是54.70.30.5669待定待定0.1340是64.90.30.2114待定是0.0836是71.10.12.1446是是0.2195是81.30.11.4146待定待定0.2060是91.70.11.0503待定待定0.1885是102.10.10.5138待定待定0.1693是112.30.10.2865待定是0.1623是

通過表2得到的仿真結果，可以判斷出第1組數據所對應的回路振蕩是由控制器參數整定不當導致，后面10組數據是設置閥門黏滯特性引起的回路振蕩，然而如果利用規則一進行判斷，只有第1，2，7組能夠給出準確的結論，其他情況下均待定；如果通過規則二進行判斷，第1，2，6，7，11組能夠給出準確的結論，相比規則一準確率增大；如果通過規則三進行判斷，數據均能給出正確結論。結合指標Rs可以確切地判斷振蕩是由閥門黏滯特性引起，即該指標可檢測積分對象，彌補了峰值前后面積比值法的不足。

4 結束語

針對面積峰值法應用范圍的局限性，文中利用自衡對象和積分對象回路輸出信號二階導數的較大差異性，提出了一種改進的形狀分析方法，能夠高效且全面地進行黏滯特性檢測，解決了許多檢測方法僅適用于某一種對象的問題，但該方法計算過程中峰值的檢測易受噪聲影響，此時需要采用濾波方法提高準確性。仿真結果表明： 該方法可以準確可靠地對黏滯特性進行檢測。

[1] H?gglund T. A Control-Loop Performance Monitor[J]. Control Engineering Practice, 1995, 3(11)： 1543-1551.

[2] Ender D B. Process Control Performance： Not as Good as You Think[J]. Control Engineering, 1993, 40(10)： 180-190.

[3] ?rstr?m K J. Assessment of Achievable Performance of Simple Feedback Loops[J]. International Journal of Adaptive Control Processing, 1991, 5(01)： 3-19.

[4] Taha O, Dumont G A, Davies M S. Detection and Diagnosis of Oscillations in Control Loops[C]//Decision and Control Proceedings of the 35th IEEE Conference： IEEE, 1996(03)： 2432-2437.

[5] Capaci R D, Scali C. Review on Valve Stiction. Part I： From Modeling to Smart Diagnosis[J]. Processes, 2015, 3(02)： 422-451.

[6] 張波.控制回路振蕩、閥黏滯綜合診斷平臺的實現及工業應用研究[D].南京： 東南大學，2014.

[7] Choudhury M A A S, Shah S L, Thornhill N F, et al. Automatic Detection and Quantification of Stiction in Control Valves[J]. Control Engineering Practice, 2006, 14(12)： 1395-1412.

[8] Farenzena M, Trierweiler J O. Valve Stiction Estimation Using Global Optimisation[J]. Control Engineering Practice, 2012, 20(04)： 379-385.

[9] Capaci R B D, Scali C. Valve Stiction Quantification： a Robust Methodology to Face Most Common Causes of Loop Perturbations[C]//International Conference on Chemical and Process Engineering. Italy： Italian Association of Chemical Engineering, 2013： 1201-1206.

[10] Romano R A, Garcia C. Valve Friction Quantification and Nonlinear Process Model Identification[J]. IFAC Proceedings Volumes, 2010, 43(05)： 115-120.

[11] Kano M, Maruta H, Kugemoto H, et al. Practical Model and Detection Algorithm for Valve Stiction[C]//IFAC Symposium on Dynamics and Control of Process Systems. Holland： Elsevier, 2004： 5-7.

[12] Maruta H, Kano M, Kugemoto H, et al. Modeling and Detection of Stiction in Pneumatic Control Valve[J]. Transactions-society of Instrument and Control Engineers, 2004(40)： 825-833.

[13] Singhal A, Salsbury T I. A Simple Method for Detecting Valve Stiction in Oscillating Control Loops[J]. Journal of Process Control, 2005, 15(04)： 371-382.

[14] He Q P, Jin W, Pottmann M, et al. A Curve Fitting Method for Detecting Valve Stiction in Oscillating Control Loops[J]. Industrial & Engineering Chemistry Research, 2007, 46(13)： 4549-4560.

[15] Kalaivani S, Aravind T, Yuvaraj D. A Single Curve Piecewise Fitting Method for Detecting Valve Stiction and Quantification in Oscillating Control Loops[C]//Proceedings of the Second International Conference on Soft Computing for Problem Solving. Springer India, 2014： 13-24.

[16] Choudhury M A A S, Shah S L, Thornhill N F. Diagnosis of Poor Control-Loop Performance Using Higher-Order Statistics[J]. Automatica, 2004, 40(10)： 1719-1728.

[17] Thornhill N F. Finding the Source of Nonlinearity in a Process With Plant-Wide Oscillation[J]. IEEE Transactions on Control Systems Technology, 2005, 13(03)： 434-443.

[18] Horch A. A Simple Method for Detection of Stiction in Control Valves[J]. Control Engineering Practice, 1999, 7(10)： 1221-1231.

[19] Daneshwar M A, Noh N M. Detection of Stiction in Flow Control Loops Based on Fuzzy Clustering[J]. Control Engineering Practice, 2015(39)： 23-34.

[20] Kano M, Maruta H, Kugemoto H, et al. Practical Model and Detection Algorithm for Valve Stiction[C]//IFAC Symposium on Dynamics and Control of Process Systems. Holland： Elsevie, 2004： 5-7.

Study on Stiction Characteristics Detection Methods With an Improved Shaped Analysis

Kong Jie, Tian Xuemin, Shang Linyuan

(College of Information and Control Engineering, China University of Petroleum(East China), Qingdao, 266580, China)

Valve stiction is one of the main causes for control loop oscillation in industrial processes. Most of the existing control valve stiction detection methods are based on specific assumptions. It is only applicable for a specific scope. Aiming at the limitation that area peak method is only applicable to self-regulating object, an improved shaped analysis method is presented. Based on shape difference of loop output for self-regulating object and integral object, the larger difference for second derivative signal of vibration loop error and original signal are distinguished to conduct stiction characteristics detection. The method overcomes the limitation of area peak method only applicable to a particular range. The simulation experiment validates effectiveness and reliability of proposed method.Key words： stiction characteristics; oscillation diagnosis; control valve; nonlinear characteristics

國家自然科學基金(61273160，61403418)；山東省自然自然科學基金(ZR2014FL016，ZR2016FQ21)；中央高校基本科研業務費專項資金資助(13CX05021A，15CX06063A)。

孔杰(1990—)，女，黑龍江人，在讀碩士研究生，主要研究方向為控制回路的振蕩檢測及診斷方法。

TP273

A

1007-7324(2017)03-0024-07

稿件收到日期： 2017-01-11，修改稿收到日期： 2017-03-06。