極限在定積分中的作用
張春紅
(湖南科技職業學院,長沙 410004 )
?
極限在定積分中的作用
張春紅
(湖南科技職業學院,長沙 410004 )
極限和定積分是高等數學中重要的基礎概念。函數的極限是高等數學中最根本的基礎概念,是承接高等數學各個知識點的支架。定積分用來解決平面上封閉曲線圍成區域的面積問題,利用和式的極限即定積分來求解這一類型的區域面積。特定結構和式的極限計算就是定積分,它是極限的一種形式,數學中用于計算封閉區域的面積,實際生活中用于計算變力做功、水的壓力、立體的體積等。極限是定積分的基石,定積分是由極限引申出來的概念。學好函數極限是基礎,也是學好定積分的關鍵。
極限;定積分;函數
極限是描述變量在某一變化過程中的變化趨勢。在生活和實踐中常常要計算某些量,如:曲線圍成的陰影部分圖形面積,幾何體體積計算,外力作用下質點在移動時所做的功的計算,不均勻密度物質的質量計算,等等。為了計算這些量的精確值,利用極限來求解。大量與這些相關的問題,盡管在表面上、形式上各不相關、各不相同,但都要求計算一個和式的極限,這就是定積分的概念。定積分是極限的一種表現形式,是極限概念的升華,是理論和實踐聯系起來的紐帶。定積分概念的引入,使得很多極限問題的求解得以簡化容易。極限和定積分相互運用,更好解決了求解極限方法的問題。
1 理論
1.1 極限概念
函數極限的定義:設函數f(x)在點x0的某一去心鄰域內有定義,如果存在常數,對于任意給定的正數不論它多么小,總存在正數,使得:當滿足不等式時,對應的函數值f(x)都滿足不等式常數就叫做函數f(x)當x→x0時的極限,記為:

極限作為微積分中最基礎的概念,是指變量在一定的變化過程中,逐漸穩定趨向于某個固定的數值。微積分中基本的概念,如:連續、微分、積分等都建立在極限理論的基礎概念之上。
1.2 定積分概念
定積分定義:
設函數f(x)在[a,b]上有界,在[a,b]中任意插入若干個分點:
a=x0 把區間[a,b]分成n個小區間,各小區間的長度依次為: Δxi=xi-xi-1,(i=1,2,∧), 在各小區間上任取一點ξi(ξi∈Δxi),作乘積f(ξi)Δxi(i=1,2,∧)并作和 記λ=max{Δx1,Δx2,∧,Δxn},若不論采取怎樣的分割法對[a,b]進行分割,也不論在小區間[xi-1,xi]上怎樣取點ξi,只要當λ→0時,和S總趨于確定的極限I,就稱這個極限I為函數f(x)在區間[a,b]上的定積分,記為: 其中稱f(x)為被積函數,f(x)dx為被積式,x為積分變量,[a,b]為積分區間,a,b分別稱為積分下限和上限。 根據定積分的定義,曲邊梯形由連續曲線y=f(x)(f(x)≥0)、x軸與兩條直線x=a、x=b所圍成。 其面積A等于函數f(x)在區間[a,b]上的定積分,即: 分析: 在定積分的定義中有兩點值得注意:第一,定積分實際上就是無窮項和式的極限。第二,定積分跟特定的連續函數有密切關聯,定積分的一般項受到特定連續函數的約束,是連續函數把某個區間分割成無窮的小區間,每個小區間上任取的函數值與區間長度的乘積的疊加。 定積分的本質是和式的極限。將函數定義域上區間[a,b]分成多個小區間,求函數在每個小區間上任一點的函數值f(ξi)與小區間長度Δxi的乘積的和,在小區間長度趨于零時,如果和式的極限存在,則稱此極限值為函數在此區間的定積分。和式極限的幾何意義表示的是x軸、函數圖形及直線x=a、x=b之間各部分曲邊梯形面積的代數和再取極限。 定積分概念的引入,運用了極限的思想,但又拓展了求解極限的方法。定積分概念的引入最初是為了求解實踐生活不規則圖形的面積,后廣泛應用于物理學中求解相關問題。 定積分是特定的一種和式的極限,定積分的概念思想可用于求解和式的極限,有些和式的極限用定積分的思想才能更簡潔地解答。將極限的表達式整體轉化成積分形式,應用定積分快速簡便求原極限的結果。在求解有些積分和時,轉化為極限和的形式,可以將問題化繁為簡。定積分與極限二者可以相互轉化,將問題化難為易,從而達到解決問題的目的,共同促進拓展極限問題的求解。 定積分是一種極限,極限造就了定積分,定積分又更好解決了極限中不少棘手的問題。極限與定積分是廣義與狹義的區別,是一般與特殊的區別。定積分有極限的共性又有自己的個性,是一種特殊的極限。 函數的極限是深入研究學習函數的基礎,定積分是特殊形式的極限,是函數極限的深入研究發展。定積分概念的出現解決了實際生活中不少關于和式極限的難題。學好極限是基礎,定積分是極限學以致用的橋梁,是將理論知識運用于實踐的嫁接器。 [1] 黃江.新編高等數學[M].西安:西安交通大學出版社,2015. [2] 張琳,馬祥玉.經濟應用數學[M].上海:上海交通大學出版社,2010. [3] 章學誠.高等數學(一)微積分[M].武漢:武漢大學出版社,2004. [4] 劉玉蓮.數學分析講義[M].北京:高等教育出版社,2003. Therole of limit in definite integral ZHANG Chun-hong (Hunan Vocational College of Science and Technology, Changsha 410004, China) Limit and definite integral are important basic concepts in higher mathematics. The limit of the function is the most fundamental basic concept of higher mathematics, and it is a bracket to undertake various knowledge points of higher mathematics. The definite integral is used to solve the problem of the area enclosed by the curve on the plane, and the area of this type is solved by using the limit definite integral. The limit calculation of a particular structure is definite integral, which is a form of the limit. It is used in mathematics to calculate the area of the enclosed area, and is used to cultivate variable force acting, the pressure of water and the volume of the cube in actual life. Limit is the cornerstone of definite integral, and the definite integral is the concept derived from the limit. The functional limit is the basis to learn definite integral. Limit; Definite integral; Function 2017-02-15 張春紅(1980-),女,碩士,講師。 G642 A 1674-8646(2017)08-0130-02
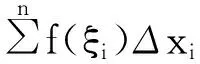
2 極限和定積分的關系
3 結語

