復雜載荷作用下壓氣機葉片疲勞壽命數值分析

張俊紅 劉 萌 付 曦 寇海軍 林建生天津大學內燃機燃燒學國家重點實驗室，天津，300072

?

復雜載荷作用下壓氣機葉片疲勞壽命數值分析

張俊紅 劉 萌 付 曦 寇海軍 林建生
天津大學內燃機燃燒學國家重點實驗室，天津，300072

為提高葉片服役壽命，在計算葉片應力分布并預測其在復雜載荷作用下的疲勞壽命后，基于逆向工程建立了三種不同精度的葉片模型；考慮離心和氣動載荷作用，求解壓氣機葉片復合載荷作用下的應力分布規律；通過葉片模擬件疲勞試驗，確定TC4鈦合金疲勞極限，擬合壽命模型參數；利用非線性連續損傷力學模型預測葉片在典型工況下的疲勞壽命。結果表明：不同模型的應力及壽命計算值存在一定差異，開展葉片數值分析時，需考慮計算模型還原葉片幾何特征的精度對計算結果的影響。

航空發動機；壓氣機葉片；逆向建模；復雜載荷；疲勞壽命

0 引言

壓氣機葉片壓縮空氣為燃燒室提供高壓氣源，長期運行在高速、高壓、高溫的環境中，隨著發動機轉速和壓比的不斷提高，葉片的服役環境愈發惡劣，因此準確預測葉片疲勞壽命、提高葉片運行可靠性是保證發動機正常運轉的關鍵[1]。

目前，葉片疲勞壽命預測主要通過疲勞試驗和數值研究開展。疲勞試驗能準確反映結構的疲勞特性，但成本相對較高；采用數值方法模擬結構的損傷行為，既易于操作又可重復實現，在降低壽命預測研究成本的同時，也可為疲勞試驗提供理論依據[2]。開展葉片疲勞數值研究，需建立葉片實體模型，考慮到航空發動機葉片曲面造型復雜[3]，在無法獲取結構設計參數的前提下，利用正向設計方法建立葉片模型存在困難。為克服這一難點，研究人員將逆向工程[4]應用于葉片三維造型，準確快速地重構葉片幾何形狀。隨著逆向建模技術日趨成熟，葉片逆向模型的曲面特征更為精確，可有效描述結構的疲勞行為，為葉片疲勞壽命的數值研究提供較為可靠的數值模型。

作為提高空氣壓力的轉動部件，引發壓氣機葉片疲勞失效的載荷種類較多，包括葉片旋轉產生的離心載荷、空氣流動產生的氣動載荷和由此激發的葉片振動載荷，以及溫度分布不均引起的熱負荷等。一般認為，壓氣機位于燃燒室前端，可忽略溫度影響，因此離心、氣動載荷是造成壓氣機葉片疲勞失效的主要載荷因素[5-7]。采用計算流體力學方法獲取葉片表面氣動參數，可準確計算葉片在復雜載荷作用下的應力分布[8-10]，確定疲勞失效危險點，結合損傷力學合理選擇疲勞模型，即可預測葉片實際工況下的疲勞壽命。

關于疲勞壽命模型，通常采用N-S曲線法[6,11]，該模型參數易擬合，滿足工程計算，但不能體現應力比、平均應力等載荷參數的影響，因此，人們將連續度概念引入疲勞研究[12]。CHABOCHE等[13]根據連續損傷力學推導的非線性連續損傷模型具有較高的計算精度。疲勞模型中包含的材料參數通常需要結合疲勞試驗數據進行擬合，以保證獲得準確的模型參數，同時可以根據疲勞試驗驗證預測模型計算結果的準確性，提高模型計算精度。

本文基于逆向工程建立葉片實體模型。由于葉片型面復雜的扭曲特性，描述葉片幾何形狀的點云數據繁多，在不影響逆向葉片扭轉特性的前提下，適當簡化曲面擬合控制條件，是保證逆向造型擬真度、降低建模復雜性的關鍵[5]，因此，本研究提出三種逆向建模方案，簡化擬合曲面的型面截線，結合計算流體力學獲取葉片在離心、氣動等復雜載荷作用下的應力分布，確定葉片危險位置的最大應力，利用Chaboche模型預測逆向葉片的疲勞壽命。

1 物理模型

1.1 計算流體力學基本方程

計算流體力學通過求解流體控制方程來預測流體運動規律，流體控制方程包括連續性方程、N-S方程和能量守恒方程。連續性方程表示為

(1)

式中，t為時間；ρf為流體密度；v為流體速度矢量。

N-S方程表示為

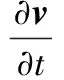
(2)

式中，ff為體積力矢量；p為流體壓力；μ為動力黏度。

對于包含熱交換的流動系統，其能量守恒方程為

(3)

式中，T為流體溫度；λ為流體熱導率；cp為質量定壓熱容；ST代表黏性耗散項。

考慮流場與結構場的相互作用，在耦合交界面處需滿足以下方程：

(4)

式中，n為方向矢量；τ為應力；df為流體位移；ds為固體位移。

1.2 疲勞壽命預測方法

連續損傷力學基于連續介質的熱力學理論研究結構的損傷演化行為，考慮損傷累積過程中材料力學性能退化對疲勞失效行為的影響，將結構的疲勞壽命看作是損傷變量連續累積直至破壞發生的一個完整過程。

CHABOCHE等[13]基于連續損傷理論，提出了一個描述損傷變量D與載荷參數σ非線性關系的損傷累積方程，其微分表達式為

dD=f(D,σ)dN

(5)

式中，N為壽命循環數。

該方程認為加載參數與損傷變量具有不可分離性，當外載為應力時，Chaboche模型表達式如下：

(6)

其中，β、M0、b為材料參數；σm為平均應力；σa為應力幅；α是與載荷、損傷都相關的參數，α表達式為

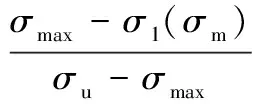
(7)

σ1(σm)=σm+σl0(1-bσm)

(8)

其中，符號〈〉定義為：當x≤0時，〈x〉=0；當x>0，〈x〉=x。σmax為循環載荷最大應力；σl0為對稱加載下的材料疲勞極限；σu為材料抗拉強度；H、α為方程相關參數，可根據疲勞試驗結果求得。

當結構未出現損傷時，D=0；疲勞破壞發生時，D=1。將式(6)從D=0到D=1積分，可以得到結構疲勞壽命表達式：

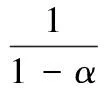
(9)

2 葉片計算模型

2.1 逆向建模方案設計

葉片為某型航空發動機高壓壓氣機五級動葉(圖1a)，葉身高154.8 mm，初始扭轉角33.4°。初始扭轉角使葉身曲面特征復雜，逆向建模時曲面擬合精度在很大程度上影響葉片的彎曲及扭轉特性，使應力及壽命的計算結果存在差異。為探求逆向建模方法對數值計算的影響，本文提出三種逆向葉片建模方案：沿葉展方向分別構造4條、6條、10條型面截線，以進排氣邊輪廓線及葉身型面截線作為限制條件，重構葉身曲面(下文分別稱為B4模型、B6模型、B10模型)。采用光學高速測量系統對葉片表面及輪廓進行三維掃描，將點云數據導入三維造型軟件，經過提取、精簡及平滑處理后，擬合葉身曲面，得到壓氣機葉片三維實體模型，如圖1所示。

(a)葉片實物 (b)B4模型 (c)B6模型(d)B10模型圖1 葉片逆向模型Fig.1 Reverse blade model

2.2 葉片有限元模型

采用十節點四面體單元對葉片三維模型進行網格劃分，建立三種逆向葉片的有限元模型，網格單元數分別為302 048、321 470、317 218。葉片三種有限元模型的網格單元數處于同一量級，消除了有限元網格劃分對計算結果精度的影響。考慮實際工作過程中，葉片與輪盤采用燕尾榫方式進行裝配，對葉片榫頭與榫槽接觸的表面施加法向約束、榫頭前后施加軸向約束。壓氣機葉片材料為TC4鈦合金，彈性模量E=107 GPa，密度ρ=4440 kg/m3，泊松比υ=0.34，抗拉強度σu=1005 MPa[14]。

2.3 葉片有限元模型驗證

葉片逆向建模時，重構曲面需進行一定簡化，造成逆向葉片與實物存在誤差，通過對比實際葉片固有頻率的試驗值與模擬仿真的計算值，進行逆向葉片擬真度的校核。

圖2所示為葉片模態試驗現場。葉片固定于試驗臺上，LMS振動測試系統連接加速度傳感器和壓電式力傳感器，通過單點激勵、單點響應的方法測試葉片的固有頻率和模態振型。壓力傳感器實時記錄激勵力，激光測振儀作為加速度傳感器，通過非接觸式測量獲取葉片激勵作用下的動態響應，將采集的信號傳入測試系統進行數據處理與分析。葉片模態試驗與有限元模擬結果如表1所示，三種逆向模型前6階固有頻率的有限元計算結果與試驗結果的相對誤差均在10%以內，保證了逆向葉片的建模精度，滿足后續分析需要。

圖2 葉片模態試驗Fig.2 Modal test of blade

對比表1前6階模態的計算值與試驗值，發現B4模型模態頻率的計算誤差相對較大，B10模型在低階的模態頻率計算值較準確，3、4、6階的相對誤差均大于其他兩個模型。對比模態頻率計算值的誤差變化規律，發現B6、B10模型均具有較小的誤差波動，且B6模型的計算結果與B10的計算結果較為接近。B6模型在保證模態計算結果較準確的同時有效降低了建模的復雜性，而B10模型具有更準確的模態計算結果，但建模過程相對最為復雜。

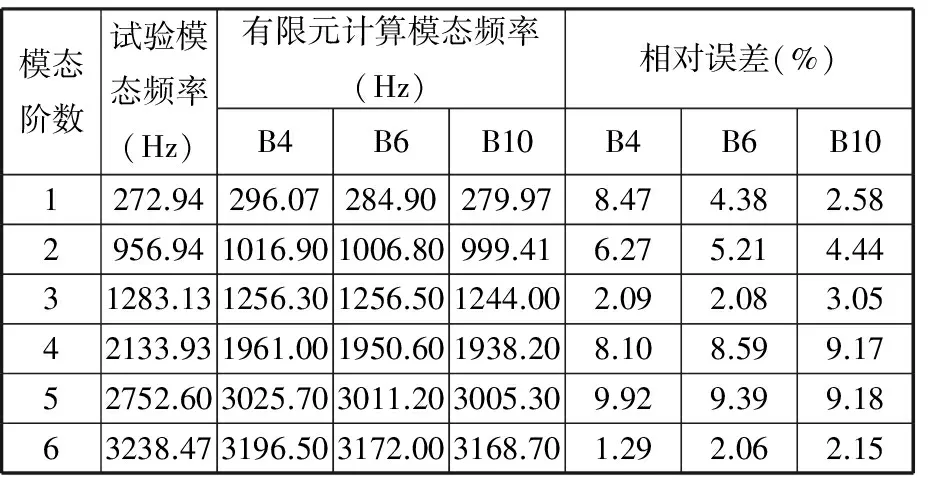
表1 葉片試驗模態與計算模態頻率對比

3 典型工況及載荷分析

3.1 典型工況

本文基于發動機試車數據，將該發動機的完整工作循環簡化為起飛、中間、最大連續、巡航和慢車5個典型工作狀態，如表2所示。統計航空發動機1000飛行小時的功率區間數據[15]，得到功率狀態分配譜(表3)。在確定發動機5個典型工作狀態的基礎上，將發動機的工作過程簡化為0-起飛-0、慢車-中間-慢車、0-最大連續-0、巡航-最大連續-巡航、慢車-最大連續-慢車5個工作循環，每種循環的轉速示意圖見圖3，相應的發動機1000飛行小時轉速循環壓縮譜如表4所示。

表2 發動機典型工作狀態

表3 發動機功率狀態分配譜(1000 h)[15]

3.2 載荷分析及流場模型

發動機運轉過程中，葉片主要受自身旋轉產生的離心載荷、氣體流動產生的氣動載荷以及由此引起的振動載荷影響。葉片在離心和氣動載荷復合作用下發生振動，會產生復雜的應力狀態，這往往是造成葉片振動疲勞失效的主因。鑒于此，本研究同時考慮離心載荷和氣動載荷的作用，進行葉片應力分布計算及疲勞壽命預測。

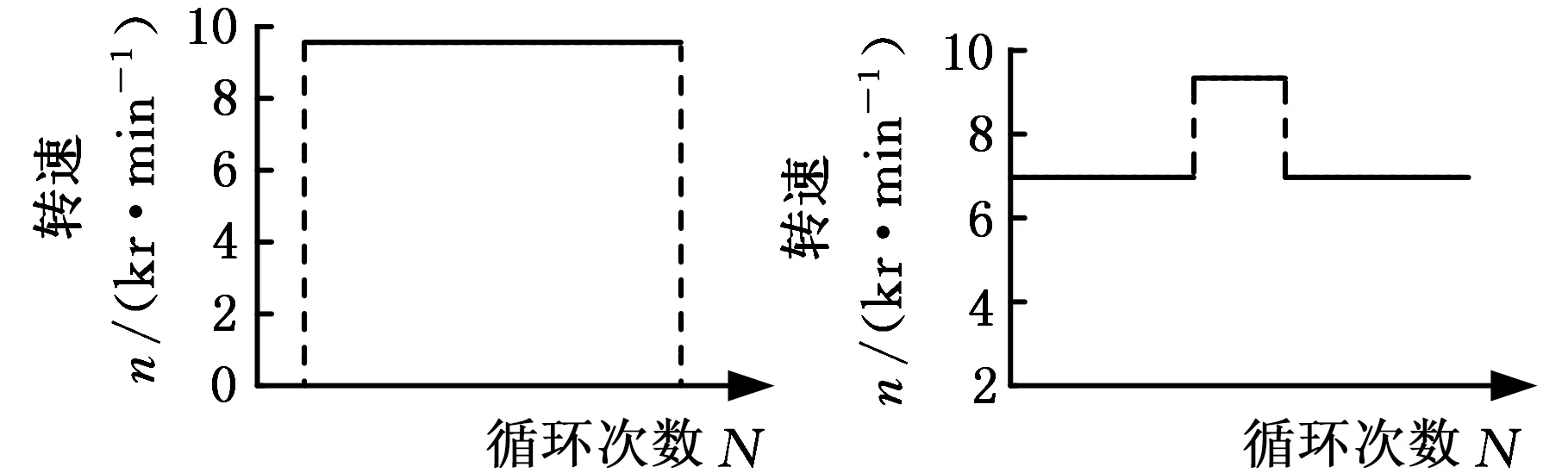
(a)0-起飛-0(b)慢車-中間-慢車

(c)0-最大連續-0(d)巡航-最大連續-巡航

(e)慢車-最大連續-慢車圖3 典型工作循環轉速示意圖Fig.3 Speed diagram of typical working conditions

表4 發動機1000飛行小時轉速循環壓縮譜[15]

為了解葉片流動特性，計算不同轉速下葉片表面承受的氣動載荷，分別以三個葉片逆向模型為基礎建立流場模型。根據該航空發動機維修手冊，設置葉尖間隙為1.7 mm，并添加進出口流道，以減小進出口邊界壓力波反射對流場計算域的影響。以6條型面截線的葉片模型為例，其流場模型和流場網格模型如圖4所示，三種葉片模型的流場網格單元、節點數量列于表5中。

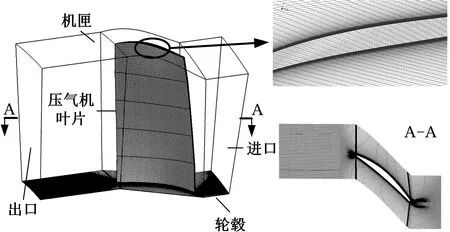
圖4 葉片流場圖和流場網格圖Fig.4 Flow field model of blade

表5 葉片流場網格單元、節點數

利用ANSYS Fluent軟件對典型工況下的壓氣機葉片表面壓力及應力分布進行數值模擬。計算流場處于湍流狀態，選擇k-ε湍流模型和標準壁面函數，利用隱式算法和二階迎風格式進行求解。

4 疲勞模型參數擬合

4.1 葉片模擬件疲勞試驗

疲勞試驗為疲勞模型提供材料參數，是壽命預測數值研究的基礎。本研究使用葉片模擬件進行疲勞試驗，在保證相似性的基礎上，降低試驗成本。根據航空工業部標準HB5277-84[16]設計鈦合金疲勞試驗模擬試件，長120 mm，兩側寬20 mm，頸縮處寬10 mm，加工后試件如圖5所示。

圖5 疲勞試件實物圖Fig.5 Test specimen

試驗在室溫和大氣環境條件下進行。試件固定于試驗臺形成懸臂梁結構(圖6)，試驗中通過試件尖端的加速度傳感器測量葉尖振幅，調節加載頻率及振動臺加速度g值來改變試件尖端振幅。試驗前標定試件尖端振幅與最大應變之間的關系(圖7)，將應變換算為應力。

圖6 疲勞試驗系統Fig.6 Fatigue test system

圖7 試件表面最大應力和葉尖振幅標定結果Fig.7 Calibration result of maximum stress and amplitude

4.2 參數擬合

疲勞試驗結果如圖8所示，以達到107個循環為標準，確定TC4鈦合金疲勞極限約為440 MPa。利用式(9)對試驗數據進行擬合得到Chaboche模型曲線，確定材料參數H=0.139，M0=4.32×108，β=0.63，b=0.000 112，Chaboche模型表達式如下：

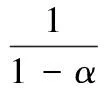
(10)

該模型考慮了平均應力和應力幅對疲勞壽命的影響，對于本研究中壓氣機葉片在不同轉速工況下的復雜受力情況，利用Chaboche模型預測疲勞壽命可以表現損傷演化過程的非線性。

圖8 TC4鈦合金葉片疲勞試驗結果Fig.8 Fatigue test results of TC4 blade

5 數值計算與分析

5.1 應力分布

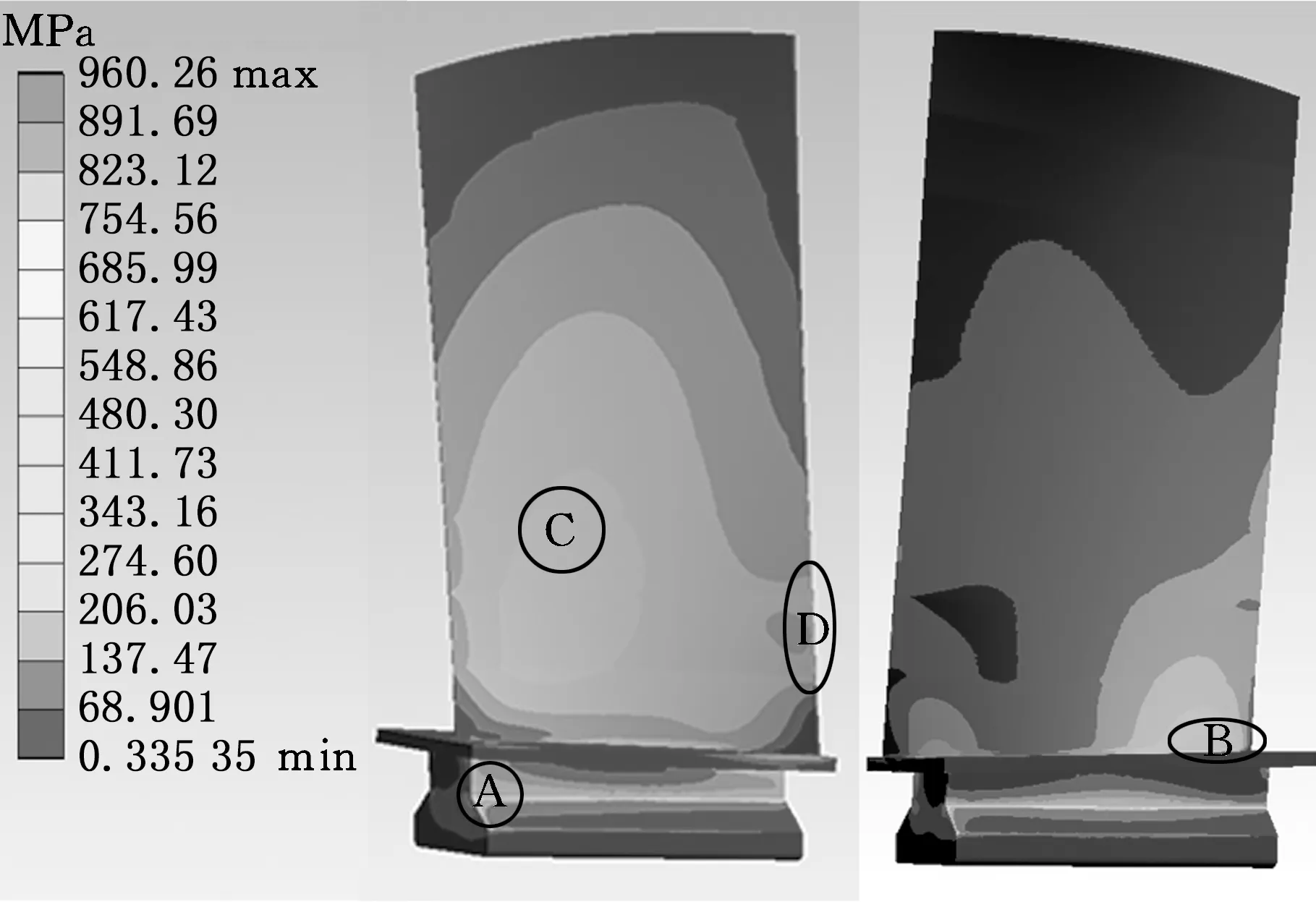
圖9 葉片應力分布及應力集中區域Fig.9 Stress distribution of blade

葉片在不同轉速工況下受離心、氣動載荷作用時的等效應力分布規律相似，以起飛工況為例進行分析，如圖9所示，應力集中區域主要包括：榫頭排氣端面A處、葉背面葉根B處、葉盆面葉身中間C處以及葉盆面進氣側距葉根約30 mm的D處。葉盆面應力分布趨勢為：C處應力較大，應力值向四周逐漸降低，且沿葉尖方向應力降幅較大，因此葉尖的應力值最小，應力主要集中在C處。葉背面應力分布趨勢為：B處應力最大，應力值沿葉展方向逐漸降低，葉尖的應力值最小，應力主要集中在葉片根部。所建立的三個葉片模型，在不同轉速工況下葉片應力分布趨勢基本相同，但應力值有所區別。進一步對比三個模型在區域A、B、C、D的最大應力隨轉速的變化規律，探討建模方案對葉片應力分布的影響。

如圖10所示，三種葉片模型在區域A、B、C、D的最大應力隨轉速的變化趨勢均為隨轉速增大而增大，但區域A應力增大的速率較區域B、C、D更快。研究認為，當轉速越高，葉片在離心、氣動載荷作用下產生的應力越大，更易導致葉片在危險位置發生疲勞失效。準確獲取葉片在較高轉速工況下的應力分布，可以保證葉片的疲勞壽命預測值更加精確。

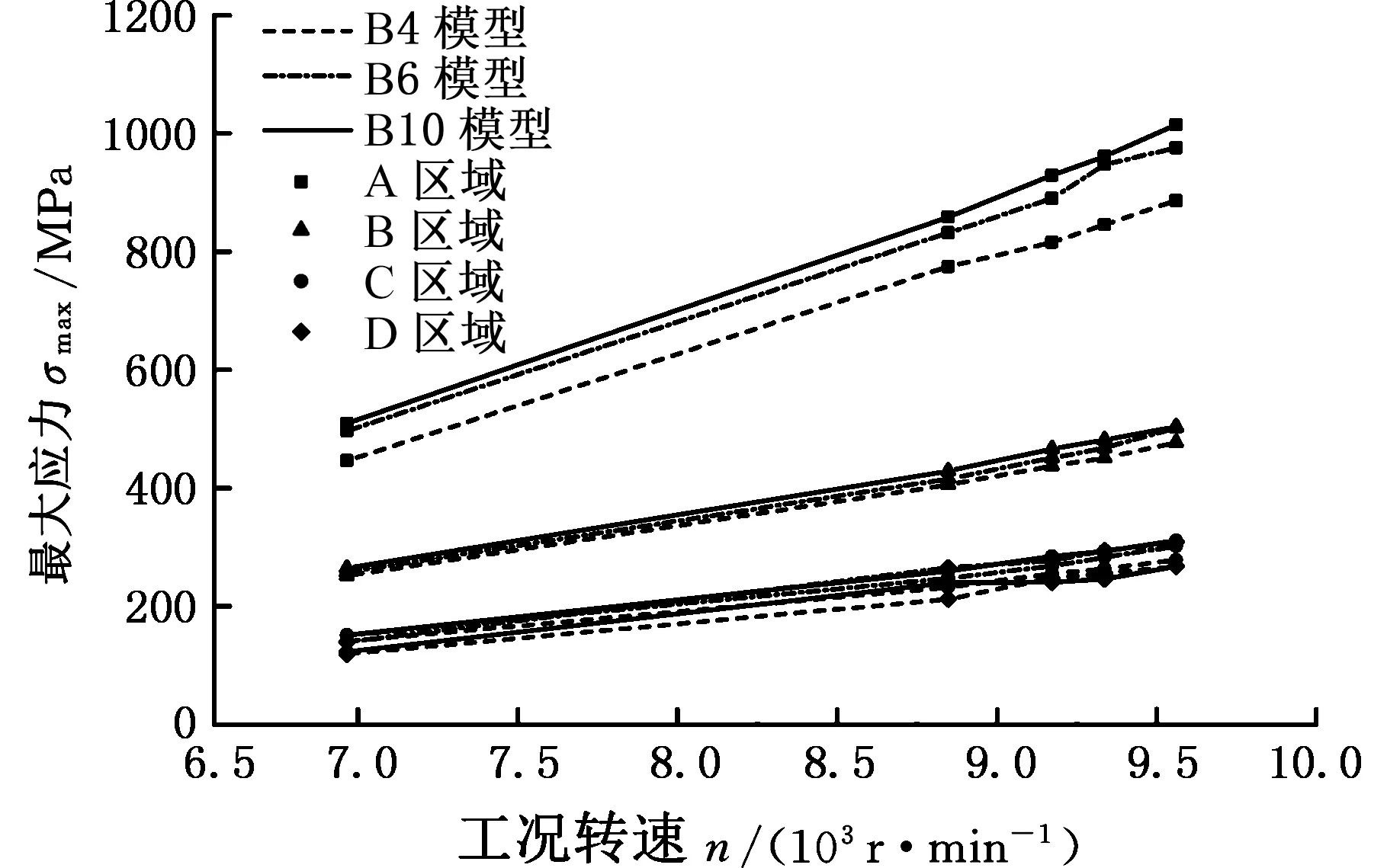
圖10 最大應力隨轉速變化曲線Fig.10 Maximum stress of blade under different rotate speed

進一步分析圖10、圖11曲線發現，不同應力集中區域在相同轉速下出現最大應力所對應的葉片模型不唯一，因此可以認為葉片建模方式對應力分布計算結果有影響，下面分別分析三種葉片模型在四個危險區域的最大應力值的變化規律。

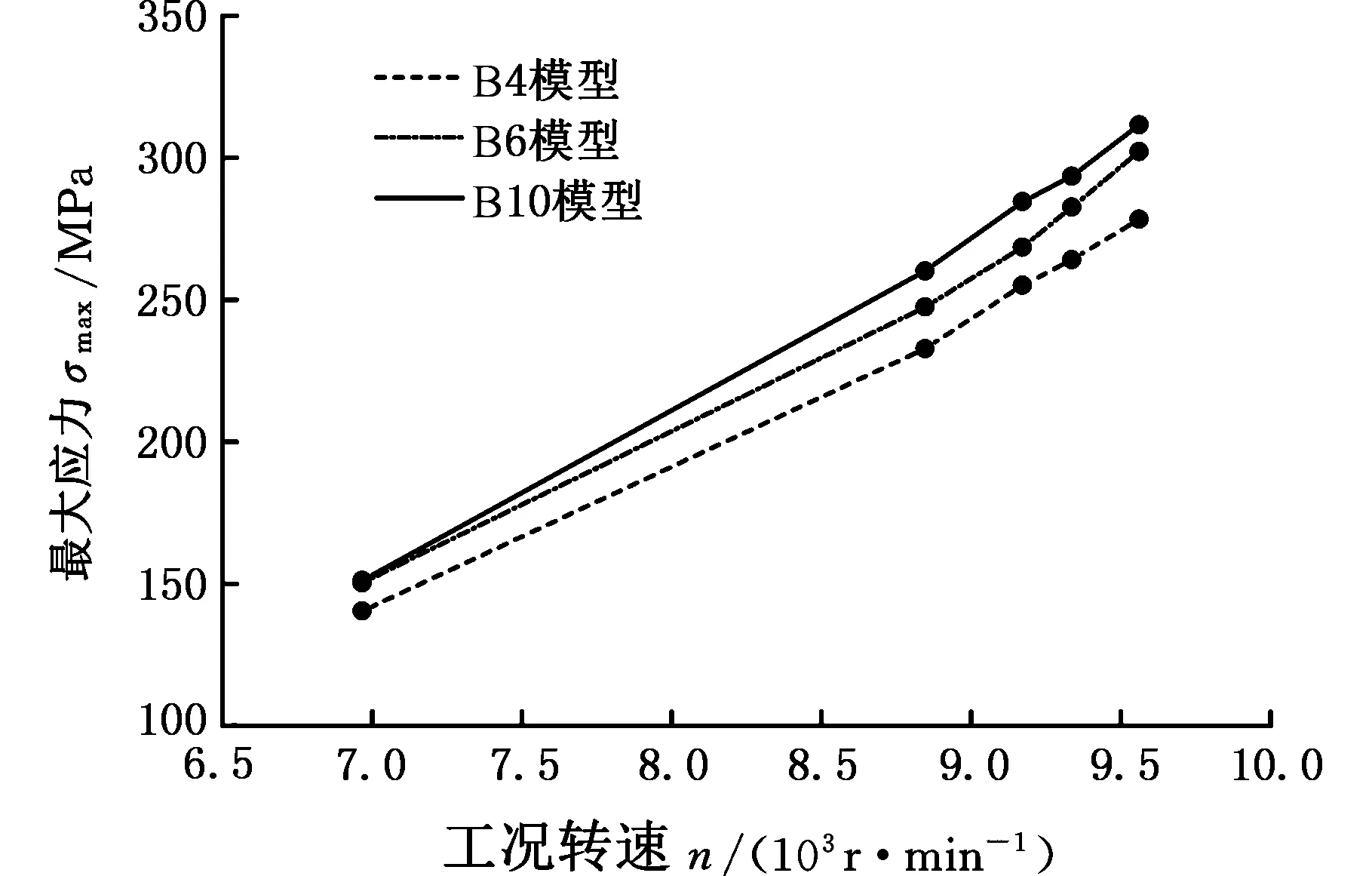
(a)區域C

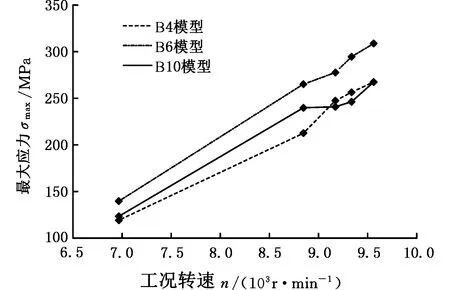
(b)區域D圖11 不同葉片模型C、D區域最大應力隨轉速變化曲線Fig.11 Maximum stress of Area C and D under different rotate speed for different blade model

榫頭排氣端面A、葉背面葉根B和葉盆面葉身中間C三個區域的最大應力值在任何轉速工況條件下均表現為：B4模型應力計算值最小、B10模型應力計算值最大，B6模型的計算值介于B4、B10之間，且與B10計算值較為接近。對比相同轉速區間，三個模型在相同危險區域的最大應力值隨轉速的增長率基本一致。但與區域A、B、C不同的是，區域D的最大應力計算值在不同葉片模型和不同工況轉速條件下的變化趨勢較為復雜。B4、B6、B10三個模型D處最大應力分別位于距葉根46 mm、35 mm、29 mm處，應力計算值隨轉速的變化規律雖然都表現為遞增關系，但相同轉速區間不同葉片模型應力的增長速率存在差異。由圖11b可以看出，B6和B10模型D處應力隨轉速的變化規律較為一致，應力增長率表現為先減小后增大；而B4模型恰好相反，最大應力的增長率為先增大后減小。上述分析說明，B4模型的計算結果較其他兩種模型存在誤差，而B6與B10模型的計算精度較為一致。

綜合分析三個模型的計算結果，認為造成上述應力分布規律變化的原因為：B10模型擬合點云數據的型面截線數較多，扭轉葉片曲面重構精度更高，受到的扭轉應力更大，因此，區域A、B、C均表現為B10模型的應力計算值最大。對于危險區域D，B10模型D處最大應力點較B4、B6模型更靠近葉根，這是由于扭轉葉片的流場特性發生變化，葉片在氣動載荷作用下受彎扭復合應力的作用，導致其最大應力點向葉根移動。比較B4、B6和B10三個模型，B10模型更好地還原了葉片的扭轉特性，但不能忽略其建模過程復雜的缺點；B6模型在簡化建模的基礎上，保證應力分布規律與B10模型基本一致，且應力計算差值較小；B4模型則存在較大計算誤差。后續研究將根據疲勞壽命的計算值進一步說明建模方案對壽命預測造成的影響。

在進行疲勞壽命研究時，理論上應選擇葉片受力較大的區域A作為危險位置。但A處的最大應力值明顯高于B、C、D三處，結合上述分析，造成A處應力集中的原因可能包括葉片榫頭建模不精確以及固支邊界條件與實際情況不完全相符。本研究旨在分析葉身應力分布情況及預測疲勞壽命，建模時簡化榫槽造型，并忽略榫槽、輪盤與榫頭的接觸及受力情況。鑒于此，以區域A作為危險位置預測葉片疲勞壽命并不準確，本文將葉背面葉根處B區域確定為危險位置，進行后續疲勞壽命研究。

5.2 壽命預測

根據葉片在離心、氣動載荷作用下的應力分布計算結果及上述應力變化規律的分析，以葉背面葉根處B區域的最大應力點作為預測疲勞壽命的危險點，參考發動機典型循環工況，編制葉片載荷譜(表6)，得到不同工況下葉片疲勞壽命預測值(表7)。

表6 危險點載荷譜

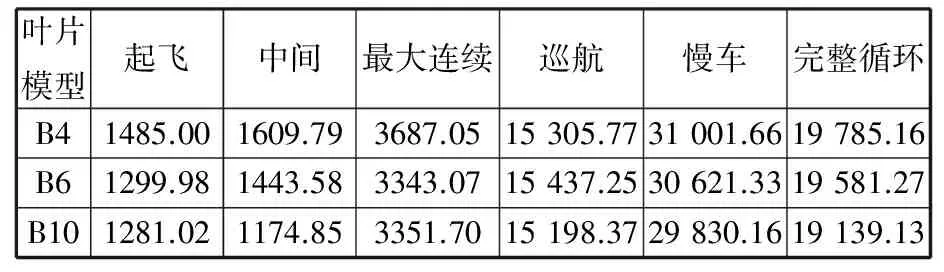
表7 葉片各工作狀態及完整循環疲勞壽命

對比表7中壽命數據可知，在起飛、中間、最大連續和慢車四個工況中，不同葉片模型的疲勞壽命計算值由大到小的順序均為：B4、B6、B10。在巡航工況，則是B6模型的壽命計算值最大，B10模型最小，B4模型的計算值介于中間。這與區域B的最大應力點在相應工況下應力值變化規律不一致，其原因主要為，葉片在危險位置的疲勞壽命不只與該點的應力有關，還與該工況下葉片所受載荷的應力比相關。因此在巡航工況，B4模型的應力計算值最小，其疲勞壽命卻略低于B6模型的結果。

根據表3給出的發動機功率狀態分配譜，計算該發動機高壓五級葉片的疲勞壽命，設起飛工況、中間工況、最大連續工況、最大巡航工況、慢車工況的疲勞壽命分別為N1、N2、N3、N4、N5，則計算公式為：1.64%N1+2.13%N2+18.83%N3+31.62%N4+45.78%N5，結果列于表7最后一列。

結果表明，本文所建立的三種逆向葉片模型，其壽命均達到19 000飛行小時，符合104飛行小時的標準，但計算值有所不同。分析發現，對于同一葉片，不同的建模方案重構葉片曲面特征的精度不同，導致應力分布和疲勞壽命計算值有所差異。對比表7三種模型完整循環的疲勞壽命，雖然差值較小，但B10模型具有更大的安全系數。綜合模態頻率及應力分布的結果，可以認為B10模型的計算精度最高，同時建模過程也最為復雜；而B6模型則在保證計算準確的基礎上，降低了建模的難度；B4模型建模方法最簡單，但計算誤差也相對較大。因此，研究認為采用數值方法開展相關計算時，應考慮建模方法對計算精度造成的影響，尤其對于包括空間曲面的復雜結構，需在簡化建模方法的基礎上，保證模型的擬真度，提高數值計算的準確性。

6 結論

(1)本文基于逆向建模理論擬合點云數據，建立了三種曲面擬合精度不同的葉片模型。利用計算流體力學，分析壓氣機葉片在離心與氣動載荷作用下的應力分布規律，結合疲勞試驗，開展葉片在典型工況下疲勞壽命研究。

(2)對葉片在離心、氣動復雜載荷作用下的應力分布及疲勞壽命進行計算，結果表明三種葉片模型的應力分布規律相似，但應力值存在差異，從而導致壽命預測結果不同，說明采用逆向工程建立葉片模型時，不同建模方案重構幾何特征的精度是影響數值計算準確性的重要因素。

(3)綜合分析模態頻率、應力分布及疲勞壽命的計算結果，發現B10模型建模的復雜性高于B4模型和B6模型，但計算精度與B6模型相差較小，說明B6模型在簡化建模方法的同時保證了實體葉片較高的擬真性。

(4)對在役葉片進行疲勞壽命數值預測時，所建立的計算模型對真實葉片損傷行為的還原度，應作為研究的重要評價指標。

(5)為了更加準確地分析不同工況加載順序及載荷差值對葉片疲勞壽命的影響，應在后續研究中進行葉片復雜載荷作用下的瞬時應力分布計算，為結構的疲勞壽命預測提供更為可靠的載荷參數。

[1] 陶春虎，鐘培道，王仁智，等. 航空發動機轉動部件的失效與預防[M]. 北京:國防工業出版社,2000:6-18. TAO Chunhu, ZHONG Peidao, WANG Renzhi, et al. Failure Analysis and Prevention for Rotor in Aero-engine[M]. Beijing:National Defence Industry Press, 2000:6-18.

[2] 石可重，趙曉路，徐建中. 重力載荷下風電葉片疲勞數值計算方法研究[J]. 太陽能學報, 2013, 34(2):181-185. SHI Kezhong, ZHAO Xiaolu, XU Jianzhong. Research on Fatigue Numerical Calculation Method of Wind Turbine under Gravity Load[J]. Acta Energiae Solaris Sinica, 2013, 34(2):181-185.

[3] LEYLEK Z, NEELY A J. Development of a Blade Parametric Modeling Methodology for Design and Analysis of Computer Experiments [C]//ASME Turbo Expo 2015:Turbine Technical Conference and Exposition. American Society of Mechanical Engineers. Montreal， 2015：V02BT39A030.

[4] YUN Z, ZHI T C, TAO N. Reverse Modeling Strategy of Aero-engine Blade Based on Design Intent [J]. The International Journal of Advanced Manufacturing Technology, 2015, 81(9/12):1781-1796.

[5] NI K, WANG X Q, MIGNOLET M. Blade Stress Estimation during Multiple Vibratory Modes[C]//Structures, Structural Dynamics, and Materials Conferences. Boston， 2013:2013-1772.

[6] 張強升. 某燃機動葉及壓氣機組件應力計算與振動分析[D].北京：清華大學, 2011. ZHANG Shengqiang. Stress Calculation and Vibration Analysis of the Gas Turbine Rotor Blade and Compressor Assembly[D]. Beijing:Tsinghua University, 2011.

[7] 栗玉領，徐勝利，楊樹樺，等. 非典型氣動荷載下壓縮機葉輪疲勞強度分析[J]. 機械工程學報, 2015, 51(9):82-89. LI Yuling, XU Shengli, YANG Shuhua, et al. Fatigue Strength Analysis of Compressor Impeller under Non-typical Aerodynamic Load [J]. Journal of Mechanical Engineering, 2015, 51(9):82-89.

[8] DHOPADE P, NEELY A J. Aeromechanical Modeling of Rotating Fan Blades to Investigate High-cycle and Low-cycle Fatigue Interaction [J]. Journal of Engineering for Gas Turbines and Power, 2015, 137(5):052505.

[9] BRANDSEN J D. Prediction of Axial Compressor Blade Vibration by Modelling Fluid-structure Interaction [D]. Stellenbosch:Stellenbosch University, 2013.

[10] 陶海亮，朱陽歷，郭寶亭，等. 壓氣機葉片流固耦合數值計算[J]. 航空動力學報, 2012, 27(5):1054-1060. TAO Hailiang, ZHU Yangli, GUO Baoting, et al. Numerical Simulation of Aeroelastic Response in Compressor Based on Fluid-structure Coupling[J]. Journal of Aerospace Power, 2012, 27(5):1054-1060.

[11] SONG X, WANG L, NIINOMI M, et al. Fatigue Characteristics of a Biomedical β-type Titanium Alloy with Titanium Boride [J]. Materials Science and Engineering:A, 2015, 640:154-164.

[12] RABOTNOV Y N, LECKIE F A, PRAGER W. Creep Problems in Structural Members[J]. Journal of Applied Mechanics, 1969, 37(1):249.

[13] CHABOCHE J L, LESNE P M. A Non-linear Continuous Fatigue Damage Model [J]. Fatigue & Fracture of Engineering Materials & Structures, 1988, 11(1):1-17.

[14] 林杰威. 渦扇發動機風扇葉片疲勞壽命評估與可靠性分析[D].天津：天津大學, 2013. LIN Jiewei. Research on Fatigue Life Estimation and Reliability Analysis of Turbofan Engine Fan Blade[D]. Tianjin：Tianjin University, 2013.

[15] 岳珠峰. 鎳基單晶渦輪葉片結構強度設計[M]. 北京：科學出版社，2008:213-232. YUE Zhufeng.Structural Strength Design of Nickel Based Single Crystal Turbine Blade[M]. Beijing:Science Press, 2008:213-232.

[16] 中華人民共和國航空工業部.HB 5277-84 發動機葉片及材料振動疲勞試驗方法[S]. 北京：中國標準出版社，1984. Ministry of Aviation Industry of China, HB 5277-84 Test Method for Vibration and Fatigue of Engine Blades and Materials[S]. Beijing:Standards Press of China, 1984.

(編輯 王旻玥)

Numerical Analyses on Fatigue Life for Compressor Blades under Complex LoadsL

ZHANG Junhong LIU Meng FU Xi KOU Haijun LIN Jiansheng
State Key Laboratory of Engines,Tianjin University,Tianjin，300072

In order to improve service life of blades, three blade models were built based on reverse engineering to calculate stress distribution and fatigue life of blades under complex loadings. Considering the influence of centrifugal loads and aerodynamic loads, stress distributions of compressor blades were solved under complex loads. Moreover, the fatigue limit and life prediction model parameters were defined through the fatigue tests, and the fatigue life of compressor blades under the typical working conditions were predicted by nonlinear continuous damage model. Comparing the differences of stress values and fatigue life among three models, results show that the restoration degree of blade geometrical features for the calculation model must be considered when numerical calculations were carried out for blades with complex torsional characteristics.

aero-engine; compressor blade; reverse modeling; complex load; fatigue life

2016-07-05

高等學校博士學科點專項科研基金資助項目(20130032130005)；天津市科技支撐計劃資助重點項目(13ZCZDGX00200)

V232.4

10.3969/j.issn.1004-132X.2017.12.009

張俊紅，女，1962年生。天津大學機械工程學院教授、博士。主要研究方向為動力機械振動及疲勞可靠性。獲中國機械工業科學技術獎一等獎1項、國家科學技術進步獎二等獎1項。發表論文130余篇。劉 萌，女，1991年生。天津大學機械工程學院碩士研究生。付 曦(通信作者)，女，1990年生。天津大學機械工程學院博士研究生。E-mail：fuxi22@tju.edu.cn。寇海軍，男，1984年生。天津大學機械工程學院博士。林建生，男，1960年生。天津大學機械工程學院研究員。