單軌車輛耦合動力學模型與振動響應特性

文孝霞, 杜子學, 許舟洲, 尹燕莉 , 隗寒冰

(1. 重慶交通大學機電與車輛工程學院 重慶,400074) (2. 重慶交通大學軌道交通研究院 重慶,400074)

?

單軌車輛耦合動力學模型與振動響應特性

文孝霞1, 杜子學2, 許舟洲1, 尹燕莉1, 隗寒冰1

(1. 重慶交通大學機電與車輛工程學院 重慶,400074) (2. 重慶交通大學軌道交通研究院 重慶,400074)

為了研究單軌車輛在設計車速范圍內的振動響應特性，進而評價單軌車輛運行平穩性與舒適性能，分析了單軌車輛走行輪、導向輪、穩定輪和轉向架中央牽引裝置及車體間的拓撲關系，利用Hamilton方程構建了包含走行輪與軌道梁頂部，導向輪、穩定輪與軌道梁側部等三向輪軌接觸對的單軌車輛空間耦合系統動力學模型,并對單軌的PC軌道梁走行面及軌道梁左、右兩側部軌面的不平度進行了數值模擬。基于空間耦合動力學模型，以軌道不平度為激勵源，設定車輛以某一恒定速度在直線軌道上運行，獲取了單軌車輛的振動響應特性，并與實車測試結果對比分析，驗證了單軌空間耦合動力學模型的正確性。在此基礎之上，獲取了單軌車輛不同設計車速下的振動響應特性，對單軌車輛的運行平穩性和舒適性進行了評價。結果表明，單軌車輛的舒適性能優良，運行平穩性能處于優秀等級。

單軌車輛；耦合動力學模型；接觸模型；軌道不平激勵；振動；平穩性

引 言

作為城市軌道交通的一種典型制式，跨座式單軌交通具有獨特的走行系統，不僅走行輪與軌道梁頂部軌面附著接觸，分布在轉向架構架邊角的導向輪與固定在構架中間兩側的穩定輪分別與軌道梁側部軌面附著接觸。單軌車輛運行過程中，軌道梁頂部軌面與兩側部軌面的不平度都將成為輸入激勵源，影響著單軌車輛的動力響應特性，從而影響單軌車輛的運行品質，制約著單軌車輛進一步推廣應用。

為獲取單軌車輛在不同工況下的動力響應特性，需建立單軌車輛空間耦合動力學模型[1-2],國內外對單軌系統的研究主要以軌道梁為研究對象，開展車橋耦合振動研究。筆者以單軌車輛為研究對象，除了單軌車輛垂向和橫向自由度外，增加考慮單軌車輛車體、前后轉向架縱向自由度。單軌與車體間牽引橡膠堆，在輪軌接觸模型中，考慮走行輪與軌道梁頂部軌面，導向輪、穩定輪與側部軌面的徑向接觸模型，研究建立較為完整的包含走行輪與軌道梁頂部，導向輪、穩定輪與側部軌面等三向輪軌接觸對的單軌車輛空間耦合系統動力學模型。以軌道梁走行面和兩個側部軌面的不平度為輸入激勵，對單軌車輛的動態響應特性進行研究。

1 跨座式單軌車輛動力學建模

1.1 單軌車輛建模

跨座式單軌車輛由車體和前、后轉向架組成，如圖1所示。其中：轉向架上走行輪通過一根驅動軸支承在構架上，走行輪與軌道梁頂部接觸，承受車輛垂直載荷并傳遞牽引力和制動力給軌道梁；4個導向輪分布在構架邊角，在軌道梁側部引導車輛沿軌道行駛；2個穩定輪對稱分布在構架中間兩側，緊靠軌道梁側面下部行駛，起著穩定車輛的作用。車體坐落在空氣彈簧上，通過中心銷牽引，中心銷上端固定在車體上，下端轉向架上的中心銷座固連，中心銷座通過牽引橡膠堆與轉向架連接。

圖1 單軌車輛轉向架圖Fig．1 The structure of the monorail bogie

建立動力學模型時，為降低模型復雜度，簡化運算，單軌車輛中涉及的彈性元件如空氣彈簧、導向輪、穩定輪與走行輪輪胎特性及牽引橡膠堆等均用線性彈簧模擬[3-4]。單軌車輛動力學模型中，考慮單軌車體及前后轉向架的縱向、橫向及垂向3個移動自由度和繞x，y，z三個軸的側滾、俯仰及搖頭轉動自由度，共計18個自由度，如圖2(a)所示。中央懸掛中的牽引橡膠堆用彈簧模擬，如圖2 (b)所示。

圖2中：M為質量；K為彈簧剛度；C為阻尼系數；x，y,z,θ分別為縱向、垂向、橫向和角位移。

采用哈密頓原理建立多自由度的大型復雜結構車輛系統動力學方程[5]

(1)

其中：T為動能；U為勢能；δW為系統保守力和非保守力所做虛功總和；δ為變分符號。

單軌車輛在軌道梁上運行時的動能、勢能和虛功表達如下

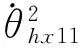
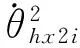
(2)

(3)

(4)

圖2 單軌車輛動力學模型圖Fig．2 Monorail vehicle dynamics model

式(3)中Rhxirjn，Rhyirjn，Rhzirjn3個方向的相對位移可以通過下式計算

Rhyi1jn=Yh11-Yv2i-θhx11Lhz1+(-1)iθhz11Lhxi

Rhvi1jn=Zh11-Zh2i+(-1)nθhx11Lhy2+

(-1)nθhx2iLhy2-(-1)iθhy11Lhxi

Rhxi2jn=Xh2i-(-1)jθhx2iLhx4+(-1)jθhy2iLhx3

Rhyi2jn=Xh2i-(-1)jθhx2iLhx3+(-1)jθhz2iLhx3

Rhvi2jn=Zh2i-(-1)jθhy2iLhx3+

(-1)nθhx2iLhy4-W02ijn

Rhxi3jn=Xh2i+(-1)jθhy2iLhx3

Rhyi3jn=Yh2i+(-1)jθhz2iLhx4+θhx2iLhx3-W03ijn

Rhvi3jn=Zh2i-(-1)jθhy2iLhx3

Rhxi4jn=Yh2i+(-1)jθhy2iLhx3

Rhyi4jn=Yh2i+θhx2iLhx3+(-1)jθhz2iLhx3-W04ijn

Rhvi4jn=Zh2i+(-1)jθhy2iLhx3

Rhxi5jn=(-1)jRhx3ijn

Rhyi5jn=(-1)jRhy3ijn

其中：W0rijn(r=2,3,4)為軌面不平位移；θhx11為車體側滾角；θhz11為轉向架搖頭角；θhx2i為轉向架側滾角；θhy2i為轉向架點頭角；θhz2i為轉向架搖頭角；Lhx1，Lhx2為車體質心到前、后空氣彈簧安裝點縱向距離；Lhx3，Lhx4為轉向架質心到導向輪、穩定輪縱向距離；Lhy2為車體質心到空氣彈簧安裝點橫向距離；Lhy3為轉向架質心到導向輪輪心距離；Lhy4為轉向架質心到穩定輪輪心距離。

1.2 輪軌接觸模型

跨座式單軌交通車輛與軌道間接觸形式獨特，走行輪與軌道梁頂部軌面、導向輪與穩定輪在預壓力作用下緊貼兩軌道側面，單軌車輛走行輪、導向輪、穩定輪與“3個軌面”附著接觸。建立走行輪與軌道梁頂部，導向輪、穩定輪與軌道梁側部軌面的接觸模型[6]。走行輪與頂部軌面法向作用力如下。

走行輪與軌道梁頂部接觸模型為

(5)

導向輪、穩定輪與軌道梁側部接觸模型為

(6)

(7)

其中：mh11為車身質量；mh2i為轉向架質量；lvx1為車身質心到前空氣彈簧距離；lvx為前后空氣彈簧距離；khvi2jn，khvi3jn，khvi4jn為走行輪、導向輪、穩定輪垂向剛度；Rhvi2jn，Rhvi3jn，Rhvi4jn為轉向架質心垂向、導向輪、穩定輪橫向相對位移；chvi2jn，chvi3jn，chvi4jn為走行輪垂向、導向輪及穩定輪徑向阻尼；Fvi3jn為走行輪與側部軌面間法向接觸力；Fvi4jn為穩定輪與軌面間法向接觸力。

2 PC軌道梁軌面不平度模擬

跨座式單軌在軌道梁上運行，軌道不平度是模型的輸入激勵源，需開展單軌車輛軌道不平度數值模擬。重慶市跨座式交通單軌PC軌道梁是預應力混凝土等截面簡支梁結構，為增大其附著力，在其表面澆筑混凝土。從跨座式單軌PC軌道梁結構和澆筑工藝可看出，PC軌道梁與鐵道車輛和地鐵車輛采用的鋼軌具有較大差異，與汽車行駛的混凝土路面具有一定相似性。因此，跨座式單軌車輛的軌道不平度模型采用ISO8608路面模型，其路面功率譜密度PSD為

(8)

其中：Ω為空間頻率(次/m)；α，β和n分別為路面粗糙度系數、形狀系數和PSD功率譜指數系數。

根據軌道梁譜數據，通過功率譜擬合，α，β和n數據取值分別如下:軌道梁頂部走行輪走行面系數取值;a=0.000 4,β=0.31,n=3.1;軌道梁側部導向輪接觸面參數取值;a=0.000 7,β=0.61,n=2.9;軌道梁側部穩定輪接觸面參數取值;a=0.000 7,β=0.5,n=2.7。

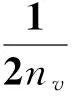
(9)

其中：Gx(nk)為功率譜密度函數；N為采樣點總數；ΔL為采樣間隔；Xm為不平度函數。

根據功率譜密度函數重構的軌道梁走行面和兩側部軌面不平度模擬[8]如圖3所示。

為比較軌面等級，再通過傅里葉變換可得軌道梁走行面、側部接觸面不平度Xm的功率譜密度，不平度模擬樣本的功率譜密度函數如圖4 所示。

圖3 軌道梁頂部、側部不平度 Fig．3 Top and side surface roughness of track beam

由圖4可知，跨座式單軌車輛軌道梁的3個軌面不平度功率譜密度等級較高，其中不同顏色的直線分別表示ISO8608車用道路A,B,C,D,E,F,G,H共8個車用道路等級，其路面功率譜密度[9]為

與ISO8608車用道路標準比較，軌道梁頂部走行面、導向面和穩定面均處于A～B等級之間。

3 單軌車輛動力學模型驗證

3.1 單軌動力學模型仿真分析

基于前述建立的模型，進行動力學仿真分析，動力學模型中各參數如表1所示。

仿真計算后，截取單軌車輛質心處橫向方向和垂向方向的加速度時間歷程的頻譜如圖5所示。

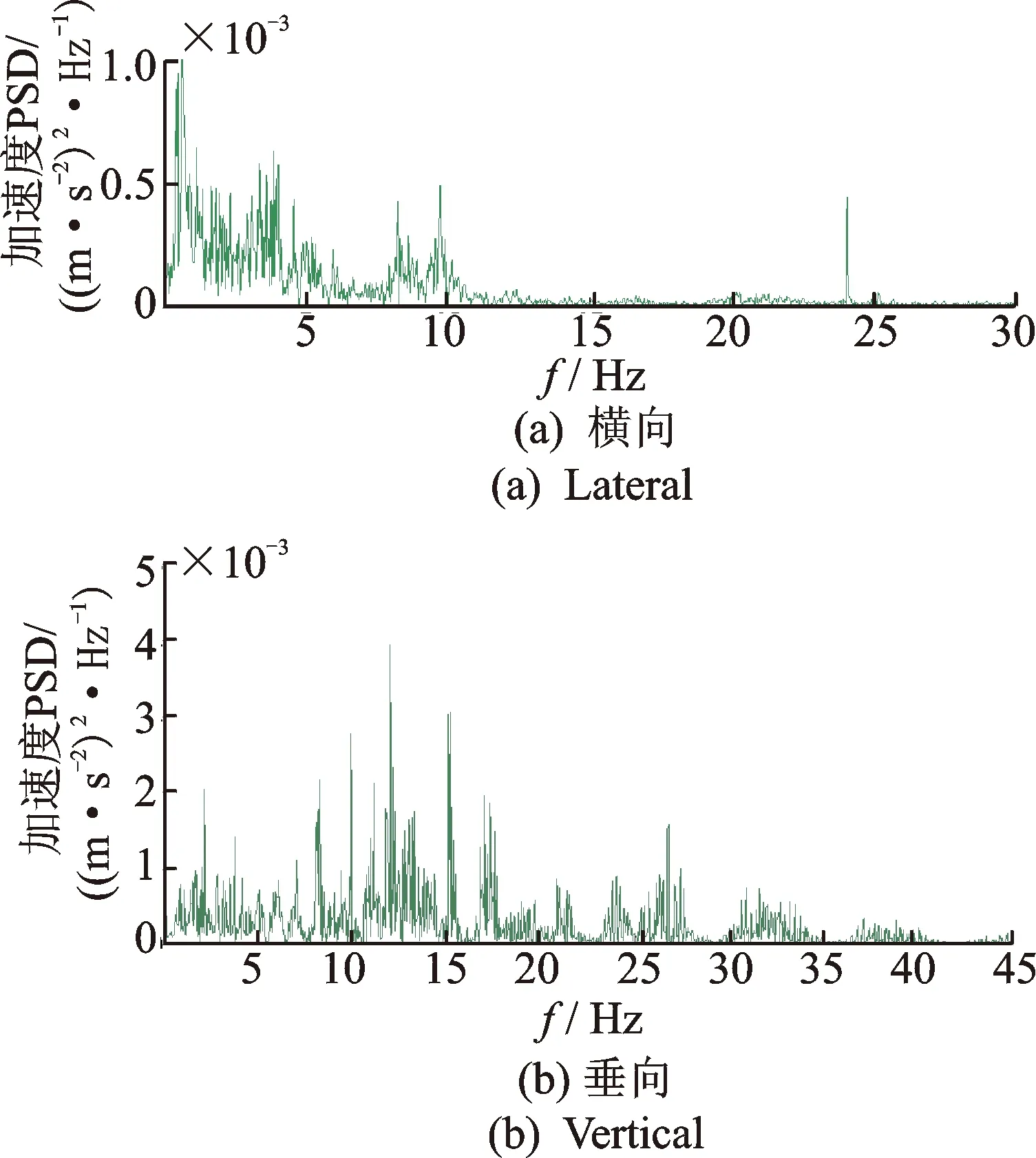
圖5 單軌車體質心加速度頻譜圖(仿真)Fig．5 Monorail centroid acceleration spectrum (simulation)

模型參數數值 單軌車體質量/kg12000單軌車體轉動慣量Ixx/(kg·m2)2×104單軌車體轉動慣量Iyy/(kg·m2)1.7×105單軌車體轉動慣量Izz/(kg·m2)1.7×105轉向架轉動慣量Ixx/(kg·m2)2400轉向架轉動慣量Iyy/(kg·m2)3400轉向架轉動慣量Izz/(kg·m2)9600走行輪轉動慣量(Iyy,Ixx)/(kg·m2)55,50走行輪x向剛度/(N·m-1)5.037×105走行輪x向阻尼/(Ns·m-1)3740走行輪y向剛度/(N·m-1)7.326×105走行輪y向阻尼/(Ns·m-1)4740走行輪z向剛度/(N·m-1)1.22×106走行輪z向阻尼/(Ns·m-1)2.6×104導向輪x向剛度/(N·m-1)3.72×104導向輪x向阻尼/(Ns·m-1)3740導向輪y向剛度/(N·m-1)4.72×104導向輪y向阻尼/(Ns·m-1)3740導向輪z向剛度/(N·m-1)9.8×105導向輪z向阻尼/(Ns·m-1)1.86×105空氣彈簧x向剛度/(N·m-1)2.32×104空氣彈簧x向阻尼/((Ns·m-1)1.01×103空氣彈簧y向剛度/(N·m-1)3.2×104空氣彈簧y向阻尼/(Ns·m-1)3.31×105空氣彈簧z向剛度/(N·m-1)1.623×105空氣彈簧z向阻尼/(Ns·m-1)2.282×104牽引橡膠堆x向剛度/(N·m-1)4.943×105牽引橡膠堆x向阻尼/(Ns·m-1)3.52×104牽引橡膠堆y向剛度/(N·m-1)4.623×105牽引橡膠堆y向阻尼/(Ns·m-1)3.25×104

3.2 仿真與試驗測試結果對比驗證

為驗證模型仿真結果的正確性，項目組采用壓力傳感器、三向加速度傳感器和德國IMC數據采集系統，如圖6所示。當單軌車輛在重慶童家院子至鄭家院子線路段直線運行時，分別對單軌車體幾何中心地板處布置三向加速度傳感器，進行了測試和采集試驗。

圖6 單軌實車振動加速度測試Fig．6 Monorail vibration acceleration test

為驗證仿真模型的正確性，將試驗測試的橫向與垂向加速度與仿真的橫向與垂向加速度頻譜圖進行對比[10]，加速度試驗數據與仿真數據在橫向與垂向兩個方向頻譜對比分別如圖7所示。

圖7 試驗與仿真頻譜對比圖Fig．7 Spectrum comparison of experimental and simulation

從圖7(a)中可看出，實測的單軌車輛橫向加速度試驗頻譜曲線在低頻段吻合較好，高頻段實測頻譜幅值稍大于仿真幅值。圖7(b)中，也可看到實測的單軌車輛垂向加速度試驗頻譜曲線在低頻段吻合較好，高頻段實測頻譜幅值稍大于仿真幅值。通過對比單軌車輛仿真加速度頻譜曲線與實測加速度頻譜曲線，在0～80 Hz頻段范圍內，幅值具有較高的一致性。單軌車輛正常行駛頻段處于低頻段，因此高頻段實測頻譜幅值稍大于仿真幅值的誤差并不會影響單軌車輛運行平穩性的評價研究。

4 單軌車輛振動響應特性分析

單軌車輛運行時，其振動響應特性直接影響車輛的運行品質，影響乘客的乘坐體驗。研究表明，車速對車輛振動特性具有較大影響[11]。現基于前面建立的單軌車輛空間耦合動力學模型,模擬當車輛分別以15，45，60和75 km/h的速度運行時，獲取單軌車輛車體質心處加速度時域歷程曲線，其中15，60 km/h的加速度時域歷程曲線如圖8，9所示。

基于仿真獲取的振動響應時程曲線，可評價單軌車輛的運行平穩性和舒適性。目前沒有制定適用于單軌車輛平穩性和舒適性的專用指標，因此，運行平穩性評價借鑒鐵道車輛動力學性能評定和試驗鑒定規范(GB5599—85)，舒適性評價采用ISO2631評價標準。

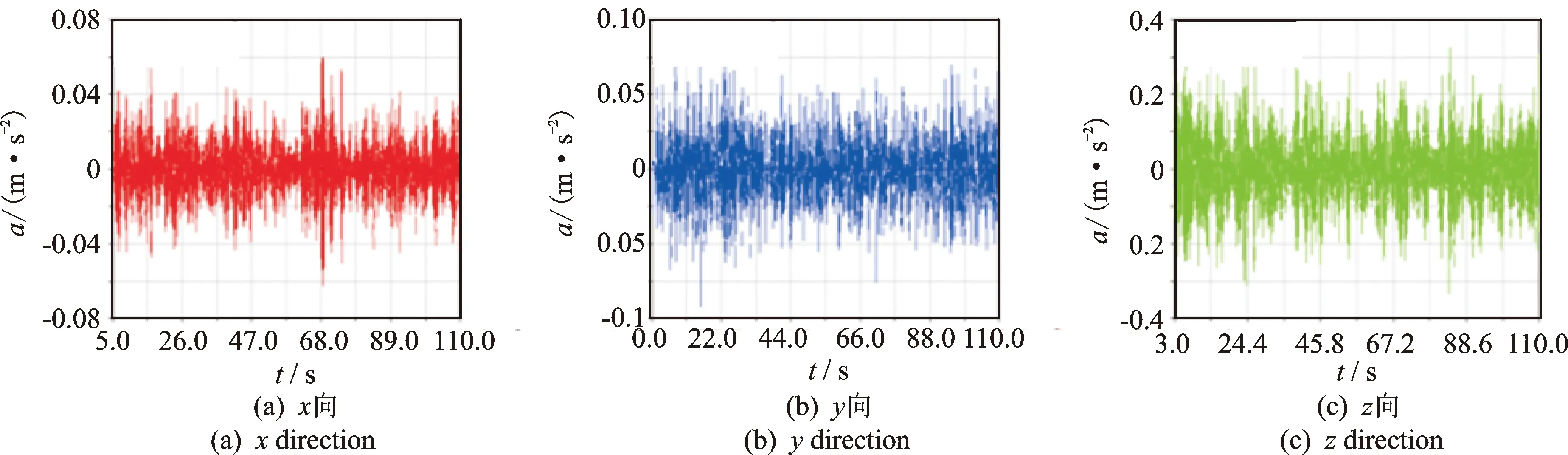
圖8 加速度時域歷程曲線(15 km/h)Fig．8 The acceleration history curve(15 km/h)

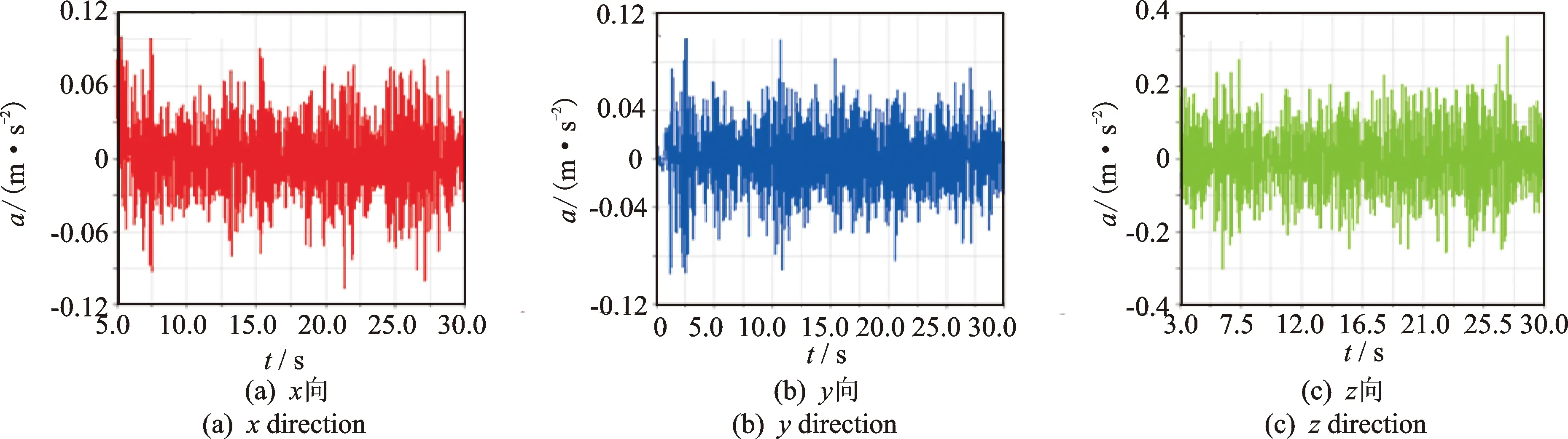
圖9 加速度時域歷程曲線(60 km/h)Fig.9 The acceleration history curve(60 km/h)

4.1 穩定性能評價分析

平穩性評價方法采用“鐵道車輛動力學性能評定和試驗鑒定規范” GB5599—85國家標準，其計算方法如下

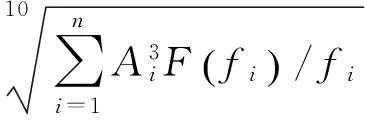
(10)

其中：W為平穩性指標；A為振動加速度；f為振動頻率；F(f)為頻率修正系數。

由于車輛振動具有隨機性和非周期性變化特點，其加速度和頻率都是隨時間而變化，且存在多種頻率成分，按式(11)對加速度時間歷程進行頻譜分析，得到每種頻率下的平穩性指數Wi，將振動按頻率進行分組，再對每一頻率成分的加速度值進行統計計算總的平穩性指標。當含有n個頻率成分時，總的平穩性指標按式(12)進行計算

按上述標準，計算15 ，45，60和75 km/h速度下單軌車輛平穩性指標，如表2所示。

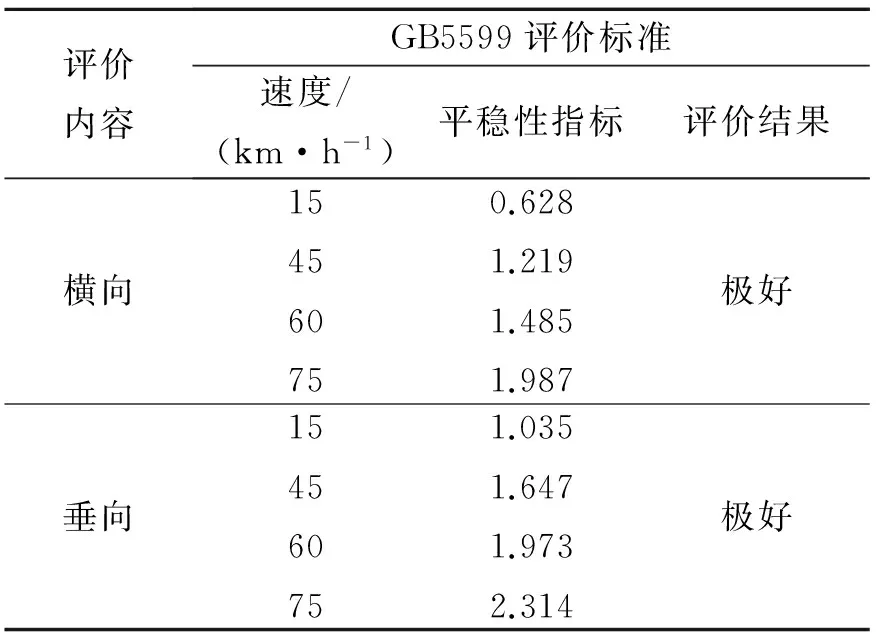
表2 平穩性評價結果

從表2中可看出，平穩性指標W均小于2.5，處于優級范圍，可評定為優級。

4.2 舒適性能評價分析

對仿真試驗獲取的加速度時域歷程a(t)進行頻譜分析可得功率譜密度函數Ga(f)，然后按照式(13)計算加速度均方根值

(13)

當有多點多軸向輸入時，可計算出各軸向加權加速度均方根值，再計算總加權加速度均方根值

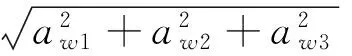
(14)

按照上述標準計算4種速度下，單軌車輛質心處加權加速度均方根值如表3所示。根據表3可知，各速度下加速度均方根值均小于舒適度臨界值0.315 m/s2，乘員不會感覺不適。

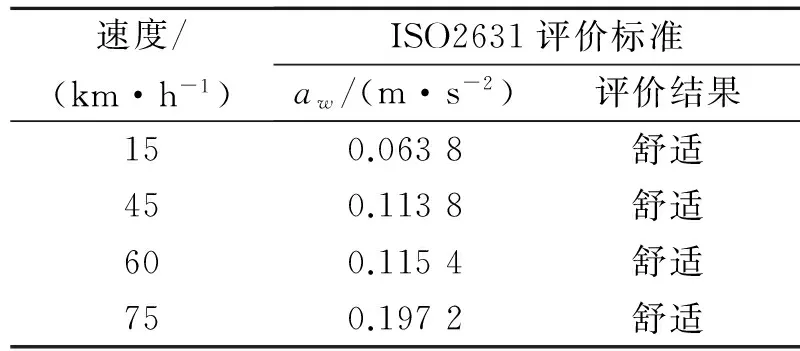
表3 舒適性評價結果

5 結 論

1) 建立了單軌車輛走行輪與軌道梁頂部，導向輪、穩定輪與軌道梁側部三向附著接觸的空間耦合動力學模型。

2) 根據離散傅里葉逆變換方法，模擬了跨座式單軌軌道梁頂部、左側和右側軌道面空間虛擬不平度激勵。

3) 通過實測單軌車輛加速度與模型仿真分析加速度幅頻特性對比分析，實測與仿真數據在幅值和頻域分布上具有較好的一致性，驗證了三向附著接觸的單軌車輛空間耦合動力學模型的正確性。

4) 基于三向附著接觸的空間耦合動力學模型，分析了單軌車輛的平穩性和舒適性。結果表明，跨座式單軌車輛舒適性良好，平穩性處于優秀等級。

[1] 馬繼兵，蒲黔輝，霍學晉. 跨座式單軌交通PC軌道梁車橋耦合振動分析[J].西南交通大學學報：自然科學版，2009,44(6):806-811.

Ma Jibing, Pu Qianhui,Huo Xuejin. Vehicle-bridge coupling vibration analysis of PC rail beam of straddle-type monorail transportation[J].Journal of Southwest Jiaotong University: Natural Science Edition,2009,44(6):806-811.(in Chinese)

[2] 劉羽宇, 葛玉梅, 楊翊仁.跨座式單軌列車與軌道梁系統的動力響應分析[J].中國鐵道科學，2010，31(5):21-27.

Liu Yuyu, Ge Yumei, Yang Yiren. The dynamic response analysis of the coupled system of the straddle type monorail train and the track beam[J].China Railway Science，2010,31(5):21-27.(in Chinese)

[3] Kenjiro G, Takaomi N. Motomi H, et al. A curving simulation for a monorail car[C]∥11th Mini Conference on Vehicle System Dynamics Identification and Anomalies. Budapest: Technical University of Budapest, 2008:15-17.

[4] Lee C H, Kawatani M, Kim C W. Dynamic response of a monorail steel bridge under a moving train[J].Journal of Sound and Vibration,2006，29(4):562-579.

[5] Diana G,Cheli F. Dynamic interaction of railway systems with large bridge[J]．Vehicle System Dynamics ,1992,18(2):100-106.

[6] Yau J D,Yang Y B, Kuo S R. Impact response of high speed rail bridges and riding comfort of rail cars [J]. Engineering Structure,2000,21(1):836-844.

[7] 杜峰,葛曉成,陳翔,等．路面功率譜密度換算及不平度建模理論研究[J] .振動、測試與診斷，2015，35(5)：981-986.

Du Feng,Ge Xiaocheng,Chen Xiang,et al. Conversion of spatial power spectral density and study on road irregularity modeling theory[J]. Journal of Vibration, Measurement & Diagnosis,2015,35(5)：981-986.(in Chinese)

[8] Lei X ,Noda N A.Analyses of dynamic response of vehicle and track coupling system with random irregularity of track vertical profile[J].Journal of Sound and Vibration,2002,258(1):147-155．

[9] Ju S H,Lin H T. Numerical investigation of a steel arch bridge and interaction with high-speed trains[J]. Engineering Structure，2003,25(6):241-250．

[10] Kawatani M, Kim C W. Computer simulation for dynamic wheel loads of heavy vehicles[J]. Journal of Structure Engineering and Mechanics，2001,12(6) :409-416.

[11] 鄭國琛,祁皚,顏學淵.考慮車軌垂向耦合福州地鐵振源加速度研究[J]. 振動、測試與診斷,2015,35(2)：328-333.

Zheng Guochen，Qi Ai，Yan Xueyuan． Research on acceleration of vibration source from Fuzhou metro considering vehicle-track vertical coupled model of vibration[J]. Journal of Vibration, Measurement & Diagnosis,2015,35(2)：328-333. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.03.007

國家自然科學基金資助項目(51475062,51305472); 重慶市基礎與前沿研究資助項目(cstc2014jcyjA60006)

2015-12-20；

2016-03-14

TH113.1; U216.3; TB124.3

文孝霞，女，1977年10月生，博士生、副教授。主要研究方向為城市軌道車輛系統動力學。曾發表《曲線工況下跨座式單軌走行輪側偏剛度對輪胎磨損的影響(《交通運輸工程學報》 2014 年第2期)等論文。 E-mail：wenxiaoxia150@163.com