一種基于小波概要的數據流量子聚類算法

米 瀅

(大連職業技術學院信息工程學院 遼寧 大連 116035)

一種基于小波概要的數據流量子聚類算法

米 瀅

(大連職業技術學院信息工程學院 遼寧 大連 116035)

針對傳統的聚類分析技術面對長度無限且隨時變化的海量級數據流無法直接使用或使用缺陷突出等問題，從數據流自身特性出發，結合小波變換與量子理論，提出一種新的數據流量子聚類算法。該算法首先采用離散小波變換，從每個數據流中動態分層地提取出其概要結構作為其相應的特征屬性，同時計算出每個數據流到聚類中心的近似距離，結合量子理論估算出較優的核寬度調節參數進行類調整，最終獲得一個較為理想的聚類效果。實驗表明，該算法較好地解決了傳統聚類方法無法良好解決的多數據流并行聚類問題，并表現出較好的聚類性能。

多數據流聚類 小波變換 量子勢能

0 引 言

隨著網絡通信、監控、實時股票行情等領域的深入發展，數據挖掘領域中涌現出了許多連續不斷且隨時間變化而演變的序列型數據，面對新的研究環境，數據挖掘的研究也迎來了新的挑戰。為此，研究者們紛紛提出了許多新的數據流聚類、分類、關聯挖掘等應用算法。概括起來，可以分為兩個方面：第一，從單條數據流出發進行挖掘，著重關注于不同時間段內數據間的隱含信息；第二，對多條數據流的挖掘，主要關注于多條數據流之間的相關性。

針對多數據流的聚類問題，文獻[1]構建SPIRIT算法來挖掘多條數據流之間的相關性，該算法利用主成分分析法，采用動態更新的策略不斷更新代表多數據流的隱藏變量及其權重；文獻[2]引入滯后相關性增量公式來發掘多條數據流之間滯后相關性的Braid算法；文獻[3]中，Yang利用概貌偏差(snapshot deviation)計算出兩個不同數據流間的加權聚合信息，以此來判斷各數據流間的相似性。文獻[4]中，Beringer等人首先利用離散傅里葉變換對原數據流進行處理，得到其低頻分量，然后利用這些低頻分量的歐氏距離來評判數據流之間的相似性；文獻[5]引入“按需聚類( Clustering on Demand)”的概念，提出了ADAPTIVEclustering算法，該算法將多數據流聚類劃分為兩個階段：在線信息的統計與維護、離線的自適應聚類。這些算法在某種程度上解決了傳統挖掘算法的一定缺陷問題，但大都忽視了數據流的遺忘特性。在數據流中，人們往往會遺忘掉比較久遠的數據或者僅需了解久遠數據的大略概況，而更多關注于數據流中的近期數據，以及近期數據的細節信息。另外，現存的算法大都采用活動窗口技術，且認為窗口中的數據可以重復存取，于是產生了較大存儲與計算的代價需求。

針對這些問題，本文充分分析了數據流的遺忘特性，引入隨時間推薦而衰減的影響因子來標注數據流中不同數據的影響力，采用離散小波變換DWT(discrete wavelet transform)適度地壓縮海量數據流。然后結合量子理論，利用改進的量子聚類算法對用概要結構表示的一組并行數據流進行聚類分析。本文將該算法稱為W-HAS-PEQC。通過實驗對比表明，該算法不僅解決了傳統聚類方法無法較好解決的多數據流并行聚類問題，而且在多數據流聚類問題上表現出良好的性能。

1 相關研究

1.1 數據的小波壓縮

面對海量級規模的數據流，在對其進行分析前先進行數據壓縮處理是很有必要的。在數據壓縮處理中，DWT[7]技術以其優異的特性越來越受研究者們的青睞，尤其是Haar小波變換，作為DWT技術中最簡單的一種，憑借著它簡單、易實現且有效的優異特性得到了廣泛的應用。

利用一維Haar小波變換，可以將向量D=(x1,x2,…,xn)分解表示為n個小波系數(c1,c2,…,cn)，我們使用一個簡單的實例來說明Haar小波變換。

例：假設某一數據序列D=(9,5,6,4,4,4,5,7)(n=8)，對其進行Haar小波變換，具體過程如表1所示。

表1 序列D的Haar小波變換

本例中，小波層次由表1中的Resolution列中的l值表示，原始數據序列存儲在l=3這一層次的Averages列中，將原數據序列中的數據項兩兩組對，求其均值記為l=2中的Averages值，即：((9+5)/2,(6+4)/2,(4+4)/2,(5+7)/2)=(7,5,4,6)，經過這一變換后，原數據序列的8個數據項將被壓縮成4個數據項，顯然丟失了原始數據序列中的某些數據信息。為了能夠重新構造出原始數據序列集，我們在保存組合后的數據對均值的同時，將該均值與原組對中第2個數據項之差也保存起來。表1中Detailcoefficients列即為數據對均值與原組對中第2個數據項之間的差值。即：(7-5,5-4,4-4,6-7)=(2,1,0,-1)，迭代重復此步驟，直至層次達到l=0，最后得到的均值與Detailcoefficients列中的全部數值即組成原數據序列的小波系數(5.5,0.5,1,-1,2,1,0,-1)。

采用樹形結構來表示該分解過程，如圖1所示，該樹稱為誤差樹。圖中節點ci(i=1,2,…,8)即為分解后的小波系數，葉子節點xi(i=1,2,…,8)為原數據序列中的數據項。以ck為根節點的子樹葉節點可劃分為左右兩個子集合：左子樹葉節點leftleavesk、右子樹葉節點rightleavesk。樹中從ck(或xk)節點到根節點的所有非零系數集合記為路徑pathk。由誤差樹可知，節點ck=(ak-bk)/2，其中k=2,3,…,n，ak為leftleavesk中數據的均值，bk為rightleavesk中數據的均值，而c1則為全部數據的均值，故原數據序列xi=∑cj∈pathiδij·cj，這里δij為一符號函數：

比如x2=+5.5+0.5+1-2=5，由此便可以重構出原始數據序列集。

圖1 序列D的誤差樹

1.2 基于參數估計的量子聚類

以粒子在量子空間中的分布為主要研究對象的量子力學在數據挖掘領域里得到了越來越多的應用，尤其是在聚類分析技術中，近年來，許多學者都開始著手研究量子聚類算法[6]的研究。

量子理論中，粒子的分布狀態采用概率波函數描述，對其求解常采用有勢場約束的薛定諤方程：

(1)

式中，H代表Hamilton算子，φ表示波函數，V表示勢能函數，E表示算子H的相應能量特征，▽代表劈型算子，方程中包含了唯一的參數δ。由該方程可知，如果兩個分布空間具有相同的勢場，則其粒子的分布狀態相同；如果將粒子所在的分布空間變換為一維無限深勢阱的狀態時，則它們將集中分布在勢能等于零的某一寬度勢阱內，因此該勢能函數可以抽象地看成是一個源，當勢能逐步減少至零時，將會有更多的粒子分布在勢阱內。

反過來，由波函數φ則可以根據式(1)反推出來粒子分布的勢能函數：

(2)

研究表明，高斯函數是式(1)的一個有效解，是一個能夠有效代表粒子分布狀態的波函數。一個高斯波包形式如下：

(3)

假設某觀測樣本集為X={x1,x2,…,xi,…xn}?Rd，其中xi=(xi1,xi2,…xid)T∈Rd，則利用式(3)可將其分布表示成一個寬度為δ的高斯波包。特殊的，如果n=1，即空間里僅有一個粒子x1時，利用上述式(2)、式(3)可得到此時的勢能函數：

(4)

(5)

假設V值確定且非負，則其最小勢能值為零，由式(2)可得：

(6)

至此既可以計算出樣本的勢能。

對樣本集的聚類就相當于將樣本都聚集在勢能為零或者最小的樣本附近，因此，勢能最小的樣本即為類中心。采用梯度下降法來求解，其迭代公式為：

yi(t+Δt)=yi(t)-n(t)▽V(yi(t))

(7)

其中，初始化變量為yi(0)=xi，學習速率為n(t)，勢能梯度為▽V。

對于算法中唯一的參數δ，我們根據高斯核寬度的參數估計法，采用式(8)來估計參數δ的值。

(8)

其中，m為樣本維數，n為樣本個數。這樣，樣本集的大小、維度等信息便隱含在了參數δ的計算中，從而將樣本集潛在的結構信息隱含在了算法模型中，提高算法性能。

2 W-HAS-PEQC算法基本思想

W-HAS-PEQC算法首先動態地維護各個數據流的小波摘要，然后利用所得到的各數據流小波摘要，結合改進的量子聚類算法對其進行在線聚類分析。

2.1 數據流的小波摘要結構

遺忘特性是流數據所特有的性質，利用這一特性，算法首先利用小波變換，采用動態的方式不斷抽取出各條數據流的摘要信息，具體提取過程[8]如下：

將原始流數據中的各數據項視為第0層，當數據項的數目達到m時，就對所收集的m個數據項進行壓縮，形成第1層中的一個新數據項。伴隨原始流數據中各數據項的不斷抵達，第1層中的新數據項數目也逐漸增多，當達到某一指定值后，就對最老的M個節點進行歸并形成第2層上的1個新數據項。以此類推，便可構造出原始數據流的一個小波誤差樹。由該誤差樹的構造可知，層次越高的數據項節點所包含的原始數據越久遠，且對應的原始數據序列就越長，因此所含原始流數據的信息就越粗糙，遺忘的程度就越大。

2.2 節點歸并

假設長度為n(n為2的冪次)的兩個數據序列D1、D2，其小波分解得到的各數據節點，即小波系數為(c11,c12,…,c1n)和(c21,c22,…,c2n)，則由D1與D2串聯起來的子序列D1∪D2的小波系數(c1,c2,…,c2n)滿足：

(9)

2.3 聚類距離

數據流之間的近似距離為：

(10)

其中，S1、S2為任意兩個有q個數據節點構成的數據流，d(P1j,P2j)為S1中第j個數據節點與S2中第j個數據節點之間的近似距離，這里任意兩節點之間的近似距離計算如下：

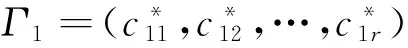
3 W-HAS-PEQC算法實現

3.1 小波摘要結構的動態維護

輸入：D，α，m，M，重構誤差ε，遺忘函數b；

輸出：小波摘要結構。

Begini0=0，j=0；

for新到達的數據項x

{i0=i0+1；x0=x；

ifi0≥m

{P=node(x1,x2,…,xm)；

iferror(P,b)<ε

//error(P,b)節點P的重構誤差

{ifj=0

{i1=1；j=1；}

苗種是水產養殖的基礎，魚苗培育工作是水產養殖的基礎工作。做好魚苗培育工作，為后續養殖提供優良的苗種，是保證養殖生產順利進行的關鍵因素。下面筆者就魚苗培育過程中的關鍵技術要點介紹如下，供養殖戶參考。

xm+1,xm+2,…?x1,x2,…；

//為0層上余下的數據重新編號

}

fork=1:j

{ifik≥M

iferror(P,b)<ε

{ifk=j

{ik+1=1；j=j+1}

elseik+1=ik+1+1；

}

}

}

}

end

3.2 W-HAS-PEQC聚類算法

W-HAS-PEQC算法的主要步驟如下：

(1) 動態維護小波摘要結構。假設我們僅需考慮長度為N的原始數據流序列，則在近似重構原始數據序列時，要選取最近的q個數據節點，要求其包含的原始數據項要大于或者等于N；

(2) 規范化取出的q個數據節點的小波系數，由式(3)初始化樣本的分布狀態，根據式(8)估算出參數δ，并根據式(7)進行算法迭代，找出類中心；

(3) 如果有新數據項到達，或者是有老數據項從數據流中刪除，則更新小波系數。每次聚類的初始化均采用前一次的聚類結果進行。

4 實驗結果與分析

為驗證算法的有效性，本文利用Matlab編程實現上述算法，并采用人工數據集與真實數據集進行實驗。其中，人工數據集是利用隨機過程分別生成的4個類別互不相同的數據集組合而成，每個類均含有100條不同的數據流序列，該數據集在實驗中，誤差樹所含的節點數目取q=4，小波系數的保留值取r=4。真實數據集采用Tickwise[10]，該數據集包含了1985年5月20日到1991年4月12日美元兌瑞士法郎的實時匯率，共329 112個數據項，為計算方便，選取前262 144個數據項構成數據序列，另外為了驗證并行數據流的聚類性能，我們又隨機生成4個各含100條不同數據流序列的并行數據流類：

p(t)=T(t)+p′(t)

p′(t+Δt)=p′(t)+u(t)

其中，T(t)為Tickwise數據序列，p(·)代表產生每一類數據流的隨機過程，u(t)為區間[-0.01,0.01]上服從均勻分布的獨立隨機變量。

為比較不同算法的聚類質量，本文采用文獻[9]中Gavrilov等人提出的性能評估標準——“聚類相似度”作為算法評估指標。該指標客觀比較了聚類的結果與數據集本身的真實類標簽，相似度值越大，表示聚類結果越接近數據的真實類別，聚類效果越好。具體的計算公式如下：

(11)

(12)

1) 基于誤差控制小波摘要結構的數據流重構實驗

實驗設置誤差樹第一層中的每個數據項由第0層中的128個數據項濃縮而得，且每個上層中的數據項均由其下層中對應的2個數據項濃縮而得，將一個數據節點距離最頂層數據節點的節點數目的倒數作為衰減函數。圖2對比了兩個數據集的實驗結果，其中橫軸代表控制誤差ε，縱軸代表控制誤差≤ε所需要的數據節點數目。

圖2 小波摘要結構的重構

2) 不同聚類算法的對比

為驗證文中算法，本文設置了兩個對比實驗算法：一個是基于小波摘要的Kmeans聚類算法，記作W-HAS-Kmeans；一個是基于離散傅里葉變換的量子聚類算法，記作DFT-PEQC。圖3分別表示出了這3個算法在Tickwise數據集上的實驗結果。從圖3中可以看出，相比于其他兩種方法，在數據節點中保留的各個不同的小波系數下，本文提出的算法取得了最好的聚類相似度值，W-HAS-Kmeans算法也取得了較好的聚類相似度，DFT-PEQC算法的聚類結果相對較差一些。

圖3 不同算法的實驗結果

通過實驗對比可以發現，基于小波變換的數據壓縮算法具有更加良好的性能，能夠在最小的誤差下保留原數據流的主要特征，同時該算法能夠去除數據流中的某些噪聲，有利于改善聚類質量。另外，相比于Kmeans聚類算法，基于量子理論的量子聚類算法能夠在一定程度上克服Kmeans算法的固有缺陷，在多數據流的聚類上具有更為優異的效果。

5 結 語

本文針對多數據流的聚類問題展開探討，設計出了一種新的數據流量子聚類算法。該算法充分考慮了數據流的遺忘特性，利用動態維護的小波摘要結構和改進的量子聚類算法，對并行的多數據流進行聚類分析。實驗表明，所提方法在并行的多數據流聚類問題上表現出了更好的聚類性能。

[1]PapadimitriouS,SunJ,FaloutsosC.Streamingpatterndiscoveryinmultipletime-series[C]//Proceedingsofthe31stInternationalConferenceonVeryLargeDataBases,Trondheim,Norway,2005:697-708.

[2]DaiBR,HuangJW,YehMY,etal.Adaptiveclusteringformultipleevolvingstreams[J].IEEETransactionsonKnowledgeandDataEngineering,2006,18(9):1166-1180.

[3]YangJ.Dynamicclusteringofevolvingstreamswithasinglepass[C]//Proceedingsofthe19thInternationalConferenceonDataEngineering,Bangalore,India,2003:695-697.

[4]BeringerJ,HüllermeierE.Onlineclusteringofparalleldatastreams[J].DataandKnowledgeEngineering,2006,58(2):180-204.

[5]KeoghE,KasettyS.Ontheneedfortimeseriesdataminingbenchmarks:asurveyandempiricaldemonstration[J].DataMiningandKnowledgeDiscovery,2003,7(4):349-371.

[6] Abdulsalam H,Skillicorn D B,Martin P.Classification using streaming random forests[J].IEEE Transactions on Knowledge and Data Engineering,2011,23(1):22-36.

[7] Gilbert A C,Kotidis Y,Muthukrishnan S,et al.One-pass wavelet decompositions of data streams[J].IEEE Transactions on Knowledge and Data Engineering,2003,15(3):541-554.

[8] Chen H,Shi B,Qian J,et al.Wavelet synopsis based clustering of parallel data streams[J].Journal of Software,2010,21(4):644-658.

[9] Gavrilov M,Anguelov D,Indyk P,et al.Mining the stock market: which measure is best?[C]//Proceedings of the 6th ACM SIGKDD International Conference on Knowledge Discovery in Data Mining.New York,NY,USA:ACM Press,2000:487-496.

[10] Tickwise數據集[DS/OL].http://www-psych.stanford.edu/～andreas/Time-Series/Data/.

A DATA STREAM QUANTUM CLUSTERING ALGORITHM BASED ON WAVELET SYNOPSIS

Mi Ying

(CollegeofInformationEngineering,DalianVocationalandTechnicalCollege,Dalian116035,Liaoning,China)

In view of the traditional clustering analysis technology, faced with the problem unlimited length and always changing mass data stream can’t be directly used or the use of defects, a new data stream quantum clustering algorithm is proposed based on the characteristics of data stream, combined with the wavelet transform and quantum theory. Firstly, the discrete wavelet transform is used to extract the profile structure from each data stream as its corresponding characteristic property, and calculate the approximate distance of each data stream to the clustering center. The optimal kernel width adjustment parameters are estimated by quantum theory, and an ideal clustering effect is obtained finally. Experiments show that the proposed algorithm can solve the problem of multiple data stream parallel clustering which can’t be solved by traditional clustering method, and show good clustering performance.

Multiple data stream clustering Wavelet transform Quantum potential energy

2016-04-10。米瀅，講師，主研領域：數據挖掘。

TP391.41

A

10.3969/j.issn.1000-386x.2017.05.050