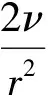帶有大初始值和真空的Navier-Stokes-Maxwell系統的整體解
孔春香
(延安大學數學與計算機科學學院, 陜西 延安 716000)
?
帶有大初始值和真空的Navier-Stokes-Maxwell系統的整體解
孔春香
(延安大學數學與計算機科學學院, 陜西 延安 716000)
考慮了Navier-Stokes-Maxwell系統的初邊值問題,借助經典的能量方法和一些先驗估計,獲得了系統的整體球對稱古典解。在這里允許真空和大初始值存在。
Navier-Stokes-Maxwell系統;整體古典解;真空;先驗估計
1 引言
在這篇文章中,我們考察(0,∞)×Ω上Navier-Stokes-Maxwell系統:
(1)
其中,ρ,u,E,H,P分別表示流體的密度、速度、電場、磁場和壓力。正常數ν和ρb表示粘性系數和背景離子密度。Ω={x∈R3:a<|x| (2) (3) u(x,t)→0,|x|→a,b,t≥0,E(x,t)→0,|x|→a,t≥0。 (4) (5) 通過(5)式直接計算得 divu=Δu,u×H=0,×H=0,×E=0。 (6) 方程(1)變為 (7) 初始條件(3)和邊界條件(4)變為: (8) u(r,t)→0,r→a,b,t≥0,E(r,t)→0,r→a,t≥0。 (9) 由方程(7),(8)進行計算得 (10) 因此(7)式又可以寫為 (11) 初始條件(8)和邊界條件(9)變為: (12) (13) 在具有初始真空和大初值條件下,Fan等[1]考慮了系統(1)的整體球對稱古典解的存在性和唯一性。Hong等[2]研究了具有洛倫茲力的可壓縮的Navier-Stokes-Maxwell 系統的初邊值問題,而且還獲得了球對稱古典解的存在性和唯一性。對于Cauchy問題,馮躍紅等[3]借助經典的能量方法和對稱技巧研究了三維全空間中Navier-Stokes-Maxwell 方程組解的漸近行為。Duan等[4]建立了三維可壓縮的系統(1)的整體解的存在性和大時間性質。 當電場和磁場不存在時,系統(1)就變成了Navier-Stokes方程組,有關Navier-Stokes方程組解的整體存在性和唯一性已有許多結果[5-7]。當磁場不存在時,系統(1)就變成了Navier-Stokes-Poisson方程組,Li等[8]獲得了整體解的收斂率估計。在壓力滿足p(ρ)=aρlogdρ下,Zhang等[9]建立了Navier-Stokes-Poisson方程組解的整體存在性。 νΔu-P(ρ0)=ρ0g, (14) 在定理的假設下,下面引理都是成立的。 引理2.1 在定理的假設下,下列估計式成立: utt∈L2(0,T;L2(a,b)), Et∈C(0,T;H2(a,b)), E∈C([0,T];H3(a,b))。 證明 見參考文獻[2]。 引理2.2 對?T>0,下列估計式成立: 證明 見參考文獻[5], m=2。 證明 由方程(11)中第2式關于r求兩次導數得 利用引理2.1和2.2得 引理2.4 對?T>0,下列估計式成立: 證明: 對(11)中第3式關于t求導,兩邊乘以Ett,利用Young不等式及引理2.1得 引理2.5 在定理的假設下,對?T>0,下列估計式成立: 證明 將(11)第2式變形得 (15) 對(15)式關于t求導得 (16) (16)式關于t求導,結果乘以r2ρ2utt,在[a,b]上積分,利用2.1, Cauchy不等式得 從而有 上式在[0,t]上積分,利用引理2.1、2.2和2.4得 由(16)式,相容性條件(14)得 從而有 (17) (16)式關于r求導得 (18) 由(17)、(18)式,引理2.1、2.2及Sobolev不等式得 引理2.6 對?T>0,下列估計式成立: 證明 見參考文獻[5],m=2。 引理2.7 對?T>0,下列估計式成立: 證明 (16)式關于t求導,結果乘以r2ρ4uttt,分部積分得 利用引理2.1、2.2、2.4、2.5、2.6和Cauchy不等式得引理2.7。 證明 對(11)中第4式關于r求三次導數,得 利用引理2.1、2.2有 對(11)中第3式分別關于r,t求導,利用引理2.1得 對(11)中第3式分別關于r求三次導數,利用引理2.1,2.2得 聯立引理2.1~2.8我們完成了定理1的證明。 [1]FAN J S, LI F C, NAKAMURA G. Uniform well-posedness and singular limits of the isentropic Navier-Stokes-Maxwell system in a bounded domain[J]. Zeitschrift für angewandte Mathematik und Physik, 2015, 66(4): 1581-1593. [2] HONG G Y, HOU X F, PENG H Y ,et al. Global spherically symmetric classical solution to the Navier-Stokes-Maxwell system with large initial data and vacuum[J]. Sci China Math,2014, 57(12):2463-2484. [3]馮躍紅,王術,雙極完全可壓縮Navier-Stokes-Maxwell 方程組光滑解的漸近行為[J].北京工業大學學報,2014.40(5):788-795. [4]DUAN R J, Green′s function and large time behavior of the Navier-Stokes-Maxwell system[J].Anal Appl,2012, 10(2):133-197. [5] DING S J, YAO L ZHU C J. Global spherically symmetric classical solution to compressible Navier-Stokes equations with large initial data and vacuum[J].J Math Anal,2012,44(2)1257-1278. [6]WEN H Y, ZHU C J. Global classical large solutions to Navier-Stokes equations for viscous compressible and heat-conducting fluids with vacuum[J]. J Math Anal, 2013, 45(2):431-468. [7] GUO Z H, LI H L, XIN Z P. Lagrange structure and dynamics for solutions to the spherically symmetric compressible Navier-Stokes equations[J].Commun Math Phy,2012, 309(2):371-412. [8]LI H L, MASTSUMURA A, ZHANG G J. Optimal decay rate of the compressible Navier-Stokes-Poisson system inR3[J].Arch Ration Mech Anal, 2010, 196(2):681-713. [9]ZHANG Y H, TAN Z. On the existence of solutions to the Navier-Stokes-poisson equations of a two-dimensional compressible flow[J].Math Methods Appl Sci,2007, 30(3):305-329. Global solutions of Navier-Stokes-Maxwell system with large initial data and vacuum KONG Chun-xiang (College of Mathematics and Computer Science, Yan′an University, Yan′an, 716000 China) ∶This work was concerned with the initial boundary value problem of Navier-Stokes-Maxwell system. By means of the classical energy method and some priori estimates, the global spherically symmetric classical solutions for this system were obtained. Here the initial data can be large and initial vacuum is allowed. ∶ Navier-Stokes-Maxwell system; global classical solution; vacuum; a priori estimate 10.3976/j.issn.1002-4026.2017.03.014 2017-05-12 延安大學校級科研計劃(YDK2015-46,YDQ2016-22);陜西省教育廳科研項目(16JK1856) 孔春香(1980—),女,碩士,講師,研究方向為偏微分方程。E-mail;chunxiang1980@163.com O175.2 A 1002-4026(2017)03-0082-06
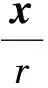
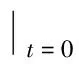
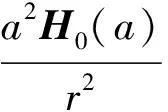
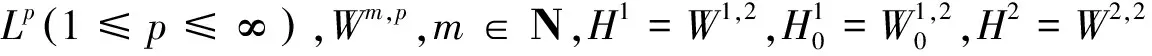
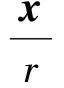


2 先驗估計