淺議仿射變換的應用

姚金江++朱萌

摘 要：變換是一種重要的數學思想。利用變換去解決問題往往可以達到事半功倍的效果。仿射變換是幾何學中的一個重要變換，是從運動變換向射影變換的重要手段。根據仿射變換的性質，可以把特殊圖形的重要結論直接推廣到一般圖形，達到復雜問題的簡單化求解。

關鍵詞：仿射變換 仿射不變性 單比

中圖分類號：TP391.41 文獻標識碼：A 文章編號：1672-3791（2017）05（a）-0156-02

仿射變換是幾何學中一個基本的變換，圖形在變換中保持許多不變性質和不變量；這些不變性質與不變量為人們解決復雜幾何問題提供了理論根據，仿射變換基本的不變性質與不變量有：同素性不變，即把直線變成直線、點變成點；平行性不變，即把平行直線變成平行直線；共線三點的單比不變，兩個三點形的面積比不變。

結論1[1] 兩個多邊形的面積之比是仿射不變量。

結論2[1] 兩個封閉圖形的面積之比是仿射不變量。

根據以上性質我們得到：三角形變為三角形（正三角形或斜三角型）、圓變為橢圓、等腰梯形變為一般梯形等。

1 應用方法

正三角形、等腰梯形、圓都是特殊的幾何圖形，有明顯的幾何性質；它們的某些性質可推廣到一般圖形中去，并可以利用相關結論解決實際幾何問題。例如正三角形3條中線把正三角形分成6個面積相等的小三角形，根據仿射性質知道，一般三角形也有這個結論。對于任意的一個一般三角形，在適當的仿射變換下，它可以變為正三角形。因此，我們要證明有關三角形的結論時，若題目中的條件都是圖形的仿射性質或仿射不變量，那么我們只需要證明這個結論在正三角形中成立即可。

任意的一個平行四邊形，經過合適的仿射變換，它可以轉換為長方形或正方形。因此要解決關于平行四邊形的符合仿射性質或數量的結論時，可以考慮正方形，只要這個結論在正方形中成立，那么它在原平行四邊形當中也成立，從而使解題過程變得簡單。

一般梯形在仿射變換下能轉化為等腰梯形。因此要解決關于梯形的符合仿射性質的題目時，可以將這個命題轉化到等腰梯形中去解決，只要在等腰梯形中成立，那么它在原梯形當中也成立。這里主要介紹一下仿射變換在梯形中證明線平行和點共線的應用。

橢圓與圓是仿射對應圖形，在仿射意義下二者等價。在解決關于橢圓的命題時，可以將此命題放到對應圓中去解決，只要命題在圓中成立，那么在橢圓中也必定成立。在高中階段，圓錐曲線問題是普遍困擾學生的一部分內容，掌握仿射變換會使一部分題目變得明朗許多，這對于數學師范學生來說是一種重要的數學思想與方法。

2 應用舉例

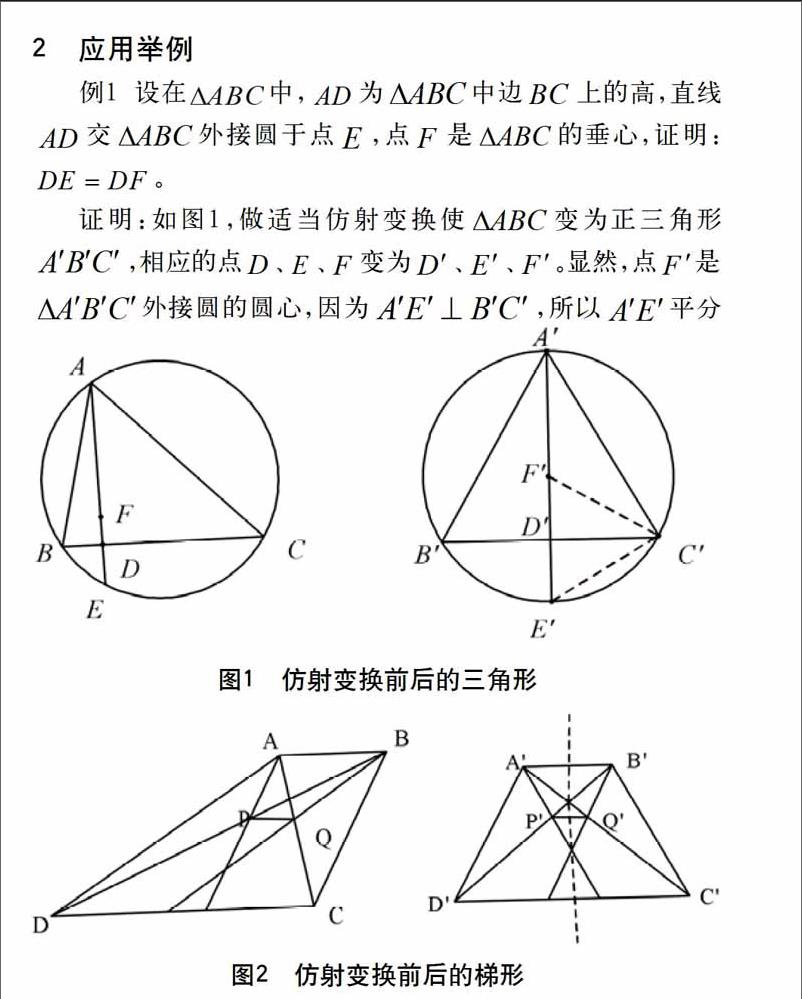
例1 設在中，為中邊上的高，直線交外接圓于點，點是的垂心，證明：。

證明：如圖1，做適當仿射變換使變為正三角形，相應的點、、變為、、。顯然，點是外接圓的圓心，因為，所以平分。

因為，

，

所以是正三角形。

因此，平分，即。

由單比是仿射不變量知。

因此。

例2 在底邊為和的梯形中，過點引平行于邊的直線且交對角線于點，而過點平行于邊的直線且交對角線于點，證明：直線平行于梯形的底邊。

分析： 該題考察梯形變為等腰梯形的仿射變換，經過變換，可以變 （是直線與的交點）為等腰三角形，因此在關于中垂線的對稱下點變為點，所以直線和平行。命題得證。

證明 如圖2所示，在適當的仿射變換下，梯形對應等腰梯形，點分別對應。

易知點與點關于梯形的中垂線左右對稱，所以

。

因為直線的平行性是仿射不變性，所以在原梯形中，

。

證畢。

例3 設橢圓方程為，求橢圓內接矩形的面積最大值。

解：如圖3所示，做仿射變換，使橢圓對應圓。設圓的半徑為，易知在圓內內接矩形面積最大時，該矩形為正方形。

橢圓的面積公式為，

根據封閉圖形的面積之比是仿射不變量得，

即，

因此矩形最大面積為。

利用仿射變換的定義、定理以及相關性質解決問題，是理論應用實踐的一種重要的思想方法。從上面的例題中可以看出，大部分題目運用仿射變換解決要簡單和方便許多，運用仿射變換可以使一些抽象的、不容易解決的問題得到很好的解決。用仿射變換解決平面幾何問題的基本思想，首先，要判斷要解決的題目是否涉及仿射性質，能否利用仿射不變性（或仿射不變量）來解決。一般來說，涉及到共線共點、線段或面積比問題的這類題目可以運用仿射變換求解。而涉及線段長度、垂直、夾角大小等，不能用仿射變換去解決。

參考文獻

[1] 姚金江，任慶軍，孫洪春.幾何學[M].北京：電子工業出版社，2010.

[2] 波拉索洛夫.俄羅斯平面幾何問題集[M].哈爾濱：哈爾濱工業大學出版社，2009.

[3] 金衛雄.談仿射性質在初等幾何中的應用[J].高等數學研究，2008，11（1）：99-101.

[4] 廖小勇.高等幾何在初等幾何中的一些應用[J].黔南民族師范學院學報，2006，1（5）：1-3.

[5] 劉增賢.高等幾何學習指導[M].北京：高等教育出版社，1989.