基于主動懸架控制輪邊驅(qū)動電動車垂向振動研究

鐘銀輝， 李以農(nóng),， 楊 超， 徐廣徽, 孟凡明

(1.重慶大學(xué) 機(jī)械傳動國家重點實驗室，重慶 400030; 2.重慶大學(xué) 汽車工程學(xué)院，重慶 400030)

基于主動懸架控制輪邊驅(qū)動電動車垂向振動研究

鐘銀輝2， 李以農(nóng)1,2， 楊 超2， 徐廣徽2, 孟凡明1

(1.重慶大學(xué) 機(jī)械傳動國家重點實驗室，重慶 400030; 2.重慶大學(xué) 汽車工程學(xué)院，重慶 400030)

針對輪邊驅(qū)動電動車存在的輪轂電機(jī)振動問題，以開關(guān)磁阻電機(jī)(SRM)為例，分析了電機(jī)垂向激勵對車輛性能的影響。探討分析不同車速工況下路面和電機(jī)兩種耦合激勵對輪邊驅(qū)動電動車垂向動力學(xué)特性的影響。研究表明，電機(jī)激勵對車輛垂向性能的影響主要集中在低車速范圍。此時，電機(jī)激勵頻率接近懸架系統(tǒng)固有頻率，容易引發(fā)車輛共振。鑒于電機(jī)激勵具有的周期性特點，提出了基于FxLMS算法的主動懸架控制方法，進(jìn)而抑制電機(jī)垂向激勵產(chǎn)生的車輛垂向振動負(fù)效應(yīng)，仿真分析驗證了算法的有效性。

輪邊驅(qū)動；開關(guān)磁阻電機(jī)；垂向激勵和響應(yīng)；FxLMS算法

為迎接21世紀(jì)能源、環(huán)境和氣候的挑戰(zhàn)，電動車呈加速發(fā)展態(tài)勢。根據(jù)動力驅(qū)動形式的不同，電動車主要分為集中驅(qū)動和輪邊驅(qū)動兩類。相對于集中驅(qū)動，輪邊驅(qū)動因具有傳動效率高、燃油經(jīng)濟(jì)性好、動力學(xué)可控性好等一系列優(yōu)點而備受關(guān)注，被視為電動車的最終驅(qū)動形式[1-2]。

目前，輪邊驅(qū)動電動車所用電機(jī)主要有異步電動機(jī)、永磁無刷電動機(jī)、開關(guān)磁阻電機(jī)(SRM)、橫向磁場電機(jī)等四類。其中，SRM具有簡單可靠、可在較寬轉(zhuǎn)速和轉(zhuǎn)矩范圍內(nèi)高效運行、控制靈活、可四象限運行、響應(yīng)速度快、可靠性好、成本較低等優(yōu)點，非常適合在電動車上的應(yīng)用；但由于SRM電機(jī)雙凸極結(jié)構(gòu)的特點，使其在實際應(yīng)用中不可避免地存在轉(zhuǎn)矩波動和振動大的缺點[3]，極大限制了其廣泛的應(yīng)用。

針對SRM振動問題，國內(nèi)外做了許多相關(guān)研究，主要涉及振動產(chǎn)生機(jī)理及其控制兩個方面。在振動產(chǎn)生機(jī)理方面，吳建華等[4]指出，電磁振動是SRM最嚴(yán)重的振動,有時可占到總振動的95%。針對SRM電磁振動，Wu等[5]基于時域研究認(rèn)為，相電壓躍變導(dǎo)致的徑向力變化率躍變是引起SRM振動大的主要原因；Cameron等[6]通過頻域研究發(fā)現(xiàn)：定、轉(zhuǎn)子間的徑向脈動磁吸力是振動和噪聲的主要來源；陳景易[7]指出，研究SRM激振力時，既要分析徑向力，也要注意切向力的影響。SRM振動控制研究主要沿著兩個方向進(jìn)行：一種方法通過對電機(jī)本體結(jié)構(gòu)的研究，確定設(shè)計參數(shù)，實現(xiàn)降低電機(jī)振動的目的。Garrigan等[8]研究了電機(jī)徑向力與電流、定子位置和氣隙長度等參數(shù)的關(guān)系，同時指出采用并聯(lián)繞組結(jié)構(gòu)可以降低電機(jī)振動。Santos等[9-10]采用多場耦合模型集成設(shè)計方法，把能耗、溫度和噪聲等作為優(yōu)化目標(biāo)，設(shè)計了一款電動車用SRM。另一種方法通過采用合適的電機(jī)控制策略來實現(xiàn)降低電機(jī)振動的目的。Doncker等[11]提出了基于平均扭矩在線計算的直接扭矩控制方法，Xue等[12]提出了把軸向位移角作為優(yōu)化目標(biāo)的控制方法，楊波等[13]提出了一種各相導(dǎo)通各項分配的轉(zhuǎn)矩分配方案。這些方法用于SRM控制均可不同程度地降低電機(jī)的垂向激勵。

綜上所述，現(xiàn)有文獻(xiàn)對SRM振動問題進(jìn)行研究，并取得了一定的成果。但是針對電機(jī)振動對車輛動力學(xué)性能影響這一問題的研究還比較少。張義民等[14]對SRM 引起的車輛振動響應(yīng)問題進(jìn)行了初步研究：推導(dǎo)了電機(jī)徑向力和切向力的解析表達(dá)式，分析了電機(jī)垂向激勵對輪邊驅(qū)動電動車垂向動力學(xué)特性的影響。本文在張義民等研究的基礎(chǔ)上，建立輪邊驅(qū)動電動車整車振動模型，進(jìn)一步探討分析不同車速工況下路面和電機(jī)兩種耦合激勵對輪邊驅(qū)動電動車垂向動力學(xué)特性的影響，并提出基于FxLMS算法的主動懸架控制，進(jìn)而抑制電機(jī)垂向激勵產(chǎn)生的車輛垂向振動負(fù)效應(yīng)。

1 輪邊驅(qū)動電動車整車模型

1.1 整車動力學(xué)方程

根據(jù)所研究問題的側(cè)重點及輪邊驅(qū)動系統(tǒng)的特殊結(jié)構(gòu)，建立前輪輪邊驅(qū)動電動車整車振動模型，如圖1所示，其中模型的驗證參考文獻(xiàn)[15]。圖中，φ，θ分別為車身側(cè)傾角和俯仰角；zb為車身質(zhì)心處垂向位移；zwij為車輪垂向位移；qij為路面不平度垂向位移輸入；F(t)ij為SRM垂向激勵；Uij為主動懸架系統(tǒng)作動力。其中下標(biāo)i取f，r，分別表示車輛前、后兩面；下標(biāo)j取l，r，分別表示車輛左、右兩面，其余各個物理量的含義及取值詳見表1。

圖1 輪邊驅(qū)動電動車整車振動模型

表1 某輪邊驅(qū)動電動車整車模型參數(shù)

Tab.1 Whole vehicle model Parameters of an in-wheel motor electric vehicle

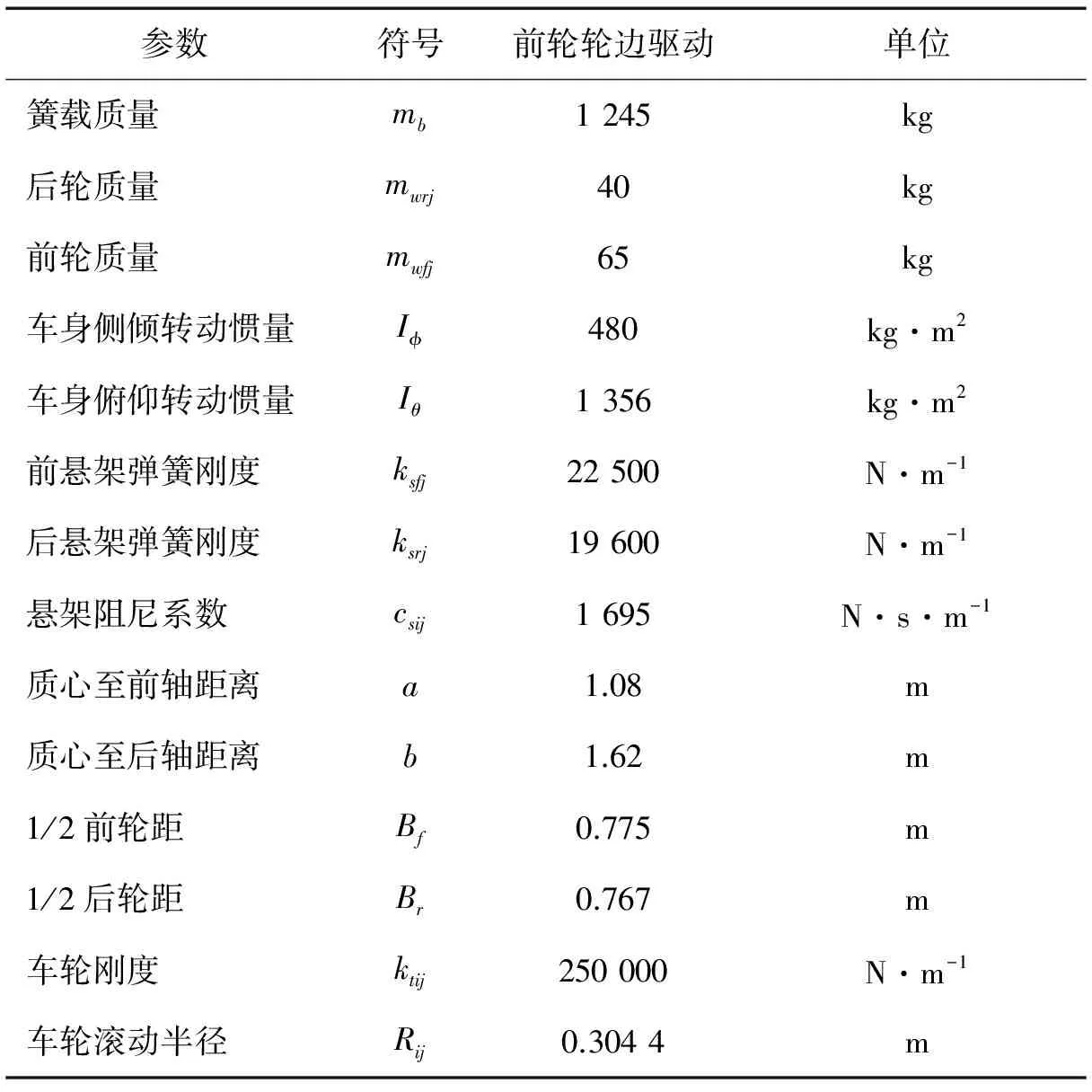
參數(shù)符號前輪輪邊驅(qū)動單位簧載質(zhì)量mb1245kg后輪質(zhì)量mwrj40kg前輪質(zhì)量mwfj65kg車身側(cè)傾轉(zhuǎn)動慣量I?480kg·m2車身俯仰轉(zhuǎn)動慣量Iθ1356kg·m2前懸架彈簧剛度ksfj22500N·m-1后懸架彈簧剛度ksrj19600N·m-1懸架阻尼系數(shù)csij1695N·s·m-1質(zhì)心至前軸距離a1．08m質(zhì)心至后軸距離b1．62m1/2前輪距Bf0．775m1/2后輪距Br0．767m車輪剛度ktij250000N·m-1車輪滾動半徑Rij0．3044m

據(jù)文獻(xiàn)[15]，推導(dǎo)輪邊驅(qū)動電動車整車動力學(xué)方程如下：

① 在俯仰角θ和側(cè)傾角φ較小時，車身四個端點處的垂向位移：

(1)

② 車身垂向動力學(xué)方程：

(2)

式中:Fz=Fsfl+Fsfr+Fsrl+Fsrr，

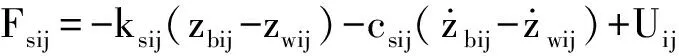
③ 車身側(cè)傾動力學(xué)方程：

(3)

式中:Mφ=Bf(Fsfl-Fsfr)+Br(Fsrl-Fsrr)。

④ 車身俯仰動力學(xué)方程：

(4)

式中:Mθ=-a(Fsfl+Fsfr)+b(Fsrl+Fsrr)。

⑤ 車輪垂向動力學(xué)方程：

(5)

1.2 SRM垂向激勵

據(jù)文獻(xiàn)[14]，SRM垂向激勵的解析表達(dá)式為

(6)

式中:T=60/(a·Nr)，a為電機(jī)轉(zhuǎn)速(r/min)；其余各個參數(shù)的意義及取值詳見表2[14]。

表2 某輪轂電機(jī)模型參數(shù)

2 仿真分析

考慮到左、右車輪內(nèi)的電機(jī)在運行過程中可能會出現(xiàn)電機(jī)初始相位角不同的情況。為了分析這種情況對整車垂向特性造成的影響，在后輪輪邊驅(qū)動電動車整車仿真分析過程中取后輪左、右電機(jī)轉(zhuǎn)子初相角分別為φl=23π/60，φr=0。10 km/h和80 km/h車速下電機(jī)的垂向激勵頻域分析如圖2所示。

在5 km/h、10 km/h、20 km/h、40 km/h和80 km/h各個車速的C級隨機(jī)路面工況下，后輪輪邊驅(qū)動電動車整車垂向性能指標(biāo)(車身垂向加速度、車身俯仰角加速度、車身側(cè)傾角加速度、懸架動行程和車輪動載荷)時域響應(yīng)的有效值如表3所示。以車身垂向振動加速度為例，10 km/h和80 km/h隨機(jī)路面工況下的頻域分析如圖3所示。

表3表明，車速對由電機(jī)垂向激勵引起的車輛垂向性能指標(biāo)響應(yīng)影響顯著。當(dāng)車速小于20 km/h時，電機(jī)垂向激勵使得車輛垂向性能指標(biāo)響應(yīng)顯著增大。當(dāng)車速為10 km/h，車輛垂向振動響應(yīng)的增幅均達(dá)到最大；此時，電機(jī)垂向激勵動對車輛的平順性和操穩(wěn)性造成了較為嚴(yán)重的破壞。當(dāng)車速大于40 km/h時，電機(jī)垂向激勵對車輛垂向性能造成的影響急劇減小，并且隨著車速的增加而進(jìn)一步弱化。當(dāng)汽車以80 km/h速度行駛時，電機(jī)垂向激勵對車輛垂向性能造成的不利影響已經(jīng)非常小。

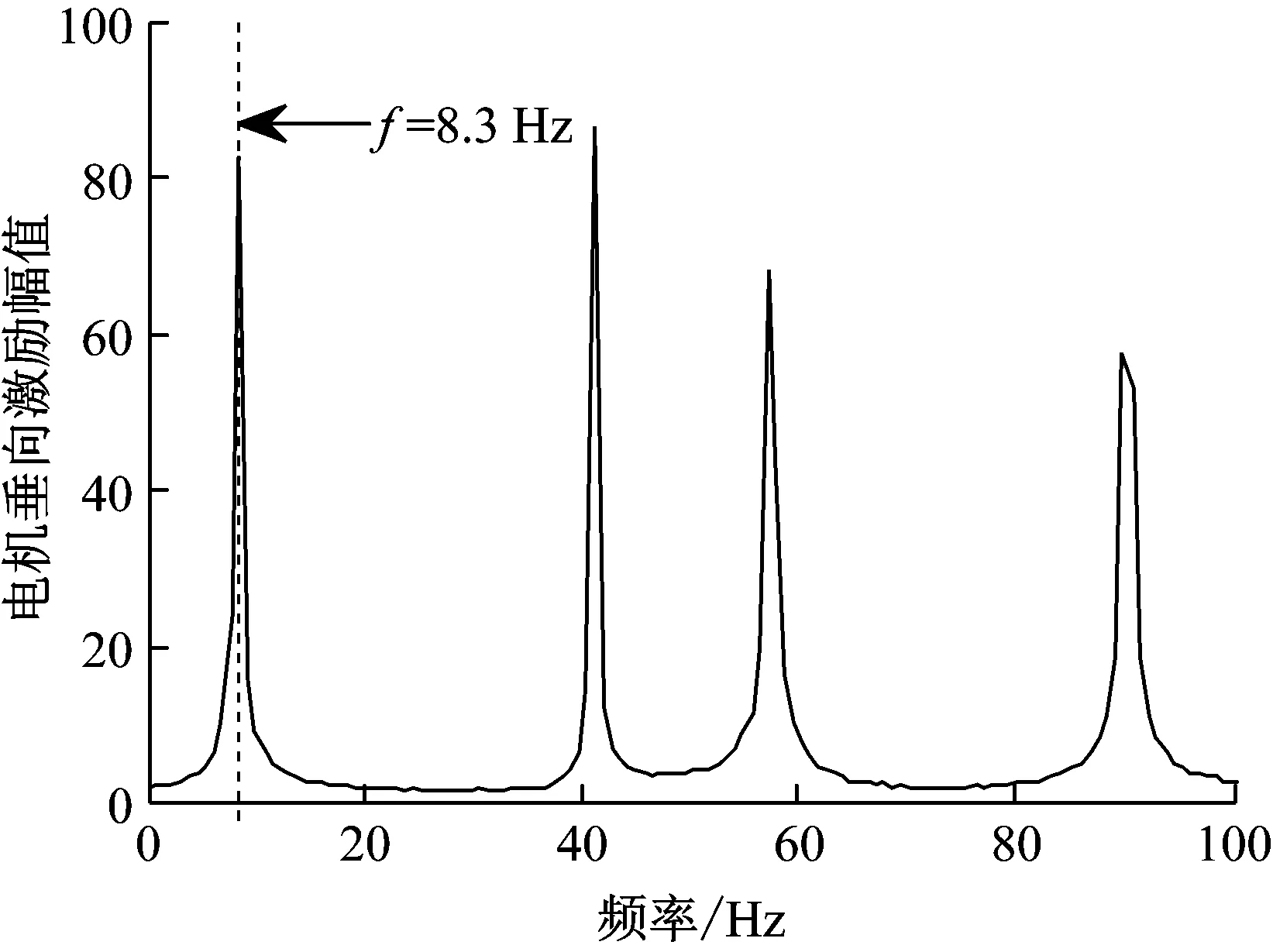
(a) 10 km/h電機(jī)垂向激勵

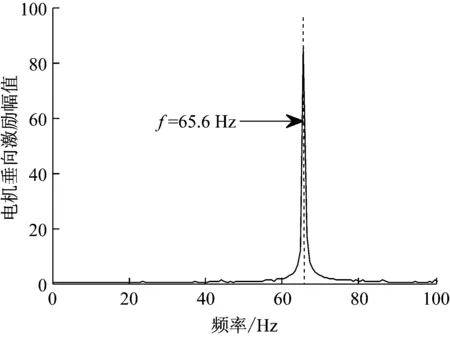
(b) 80 km/h電機(jī)垂向激勵

由圖2(a)可以看出，當(dāng)汽車以10 km/h速度行駛時，輪轂電機(jī)一階振動頻率為8.3 Hz左右。經(jīng)計算，懸架系統(tǒng)的二階(車身型)固有頻率約為10.3 Hz。顯然，電機(jī)激勵頻域接近懸架系統(tǒng)的固有頻率。對比圖3(a)同車速下的車身垂向振動加速度響應(yīng)可以發(fā)現(xiàn)，正是電機(jī)一階振動造成了懸架系統(tǒng)共振，從而使得車輛垂向動力學(xué)性能惡化。由圖2(b)可以看出，當(dāng)汽車以80 km/h速度行駛時，輪轂電機(jī)一階振動頻率為65.6 Hz左右，已超出了懸架系統(tǒng)的共振頻率范圍。對比圖3(b)同車速下的車身垂向振動加速度響應(yīng)可以發(fā)現(xiàn)，此時電機(jī)垂向激勵對系統(tǒng)動力學(xué)性能的影響很小。

綜上所述，SRM垂向激勵對輪邊驅(qū)動電動車垂向動力學(xué)性能造成的負(fù)面影響主要集中在低車速范圍。這是由于電機(jī)低速運行時，垂向激勵頻率較低，與懸架系統(tǒng)的固有頻率接近，容易引起共振，對車輛振動響應(yīng)造成非常惡劣的影響，降低車輛的平順性和操穩(wěn)性。

3 車輛垂向振動負(fù)效應(yīng)的抑制

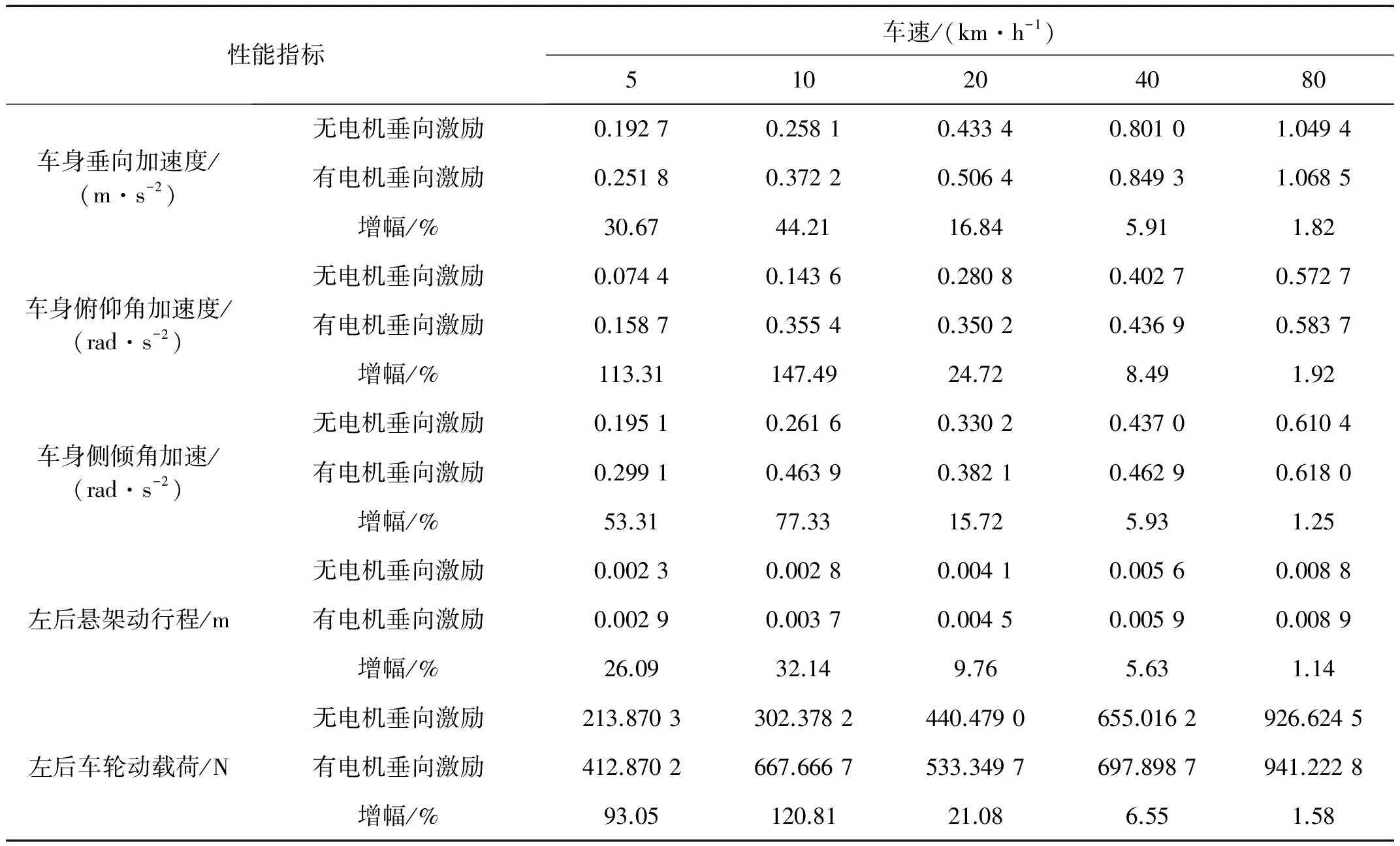
表3 C級路面激勵下車輛垂向響應(yīng)有效值

(a) 10 km/h車身垂向振動加速度響應(yīng)

(b) 80 km/h車身垂向振動加速度響應(yīng)

Fig.3 Vertical vibration acceleration response of the vehicle body under different working conditions

為解決由電機(jī)垂向激勵引起的輪邊驅(qū)動電動車振動問題，國內(nèi)外學(xué)者的研究多集中在電機(jī)本身的設(shè)計及其控制。本文另辟蹊徑，鑒于電機(jī)垂向激勵具有的周期性特點，采用基于FxLMS算法[16-18]的主動懸架控制抑制電機(jī)激勵產(chǎn)生的車輛垂向振動負(fù)效應(yīng)，改善車輛的平順性和操穩(wěn)性。

3.1 FxLMS算法原理

圖4為基于FxLMS算法的振動主動控制系統(tǒng)框圖，控制系統(tǒng)的功能分為兩部分：控制信號的推導(dǎo)和控制濾波器的加權(quán)自適應(yīng)。

圖4 采用FxLMS算法的振動主動控制系統(tǒng)

Fig.4 Active vibration control system based on FxLMS algorithm

FxLMS算法可由以下公式進(jìn)行描述：

(7)

(8)

(9)

(10)

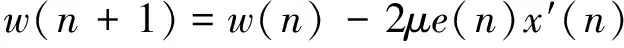
(11)

式中:各個參數(shù)的物理意義見圖4。μ為算法的迭代步長，是一個控制自適應(yīng)速度與穩(wěn)定性的增益常數(shù)[17]。

3.2 仿真分析

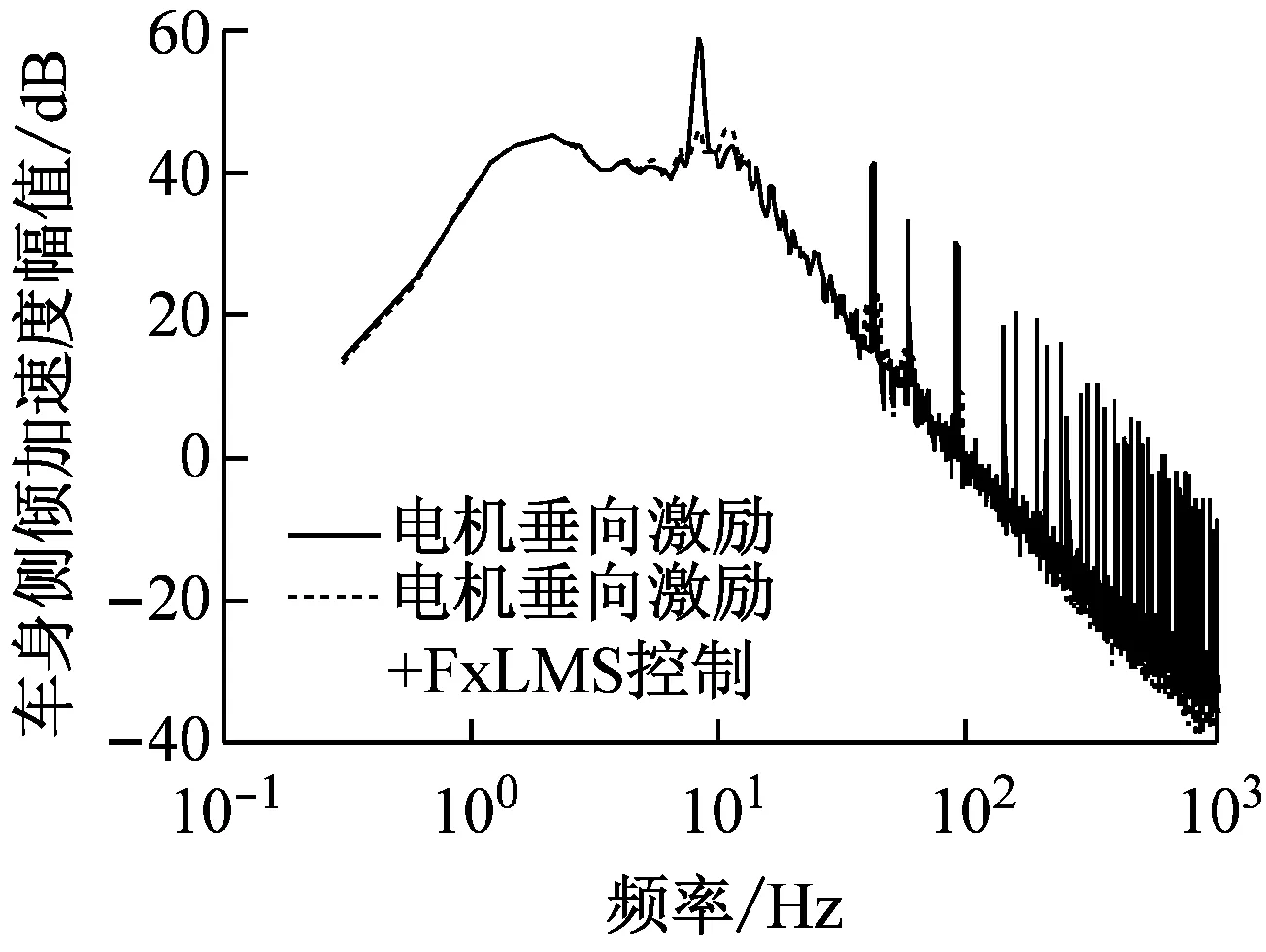
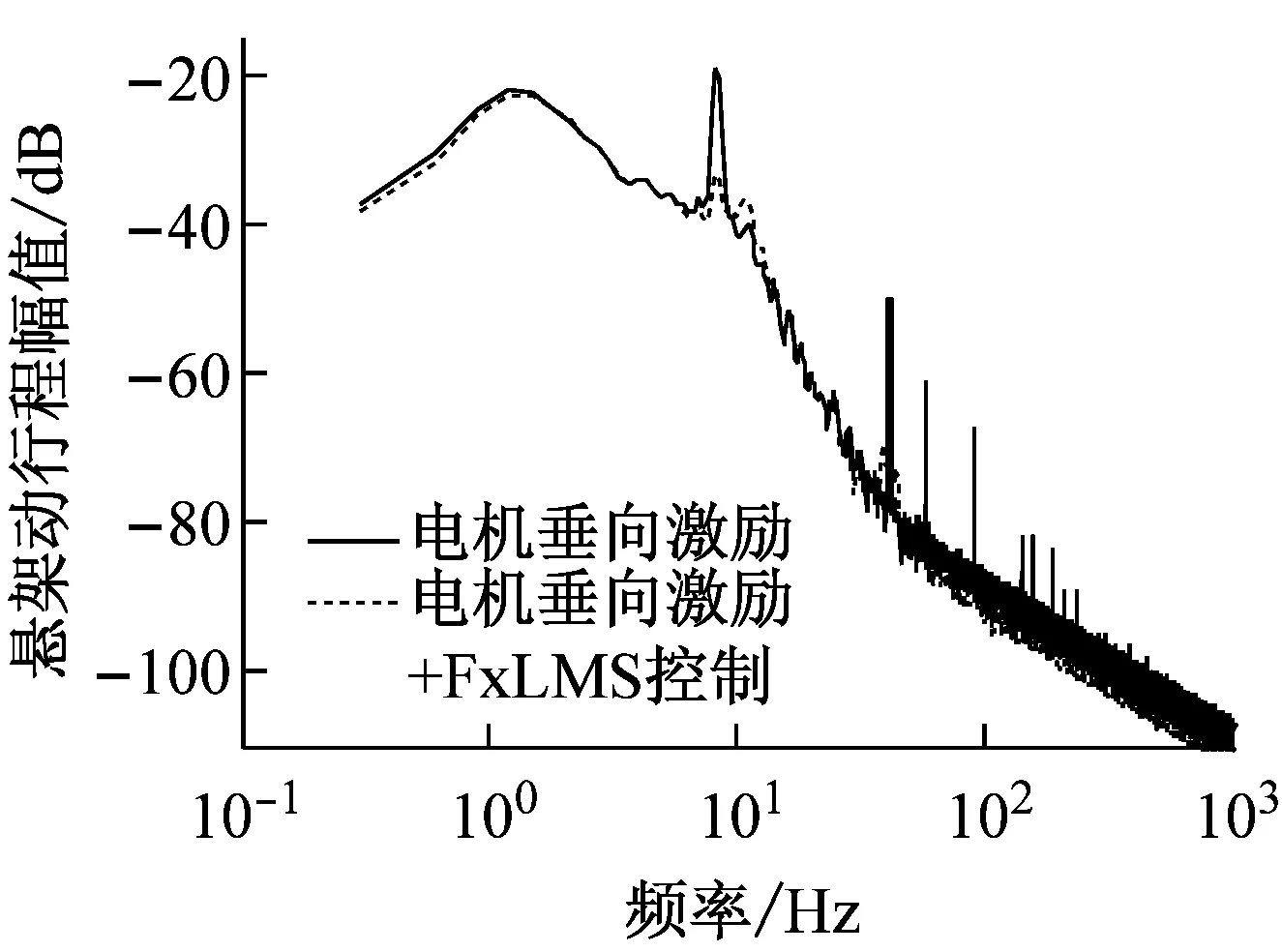
采用基于FxLMS算法的懸架主動控制抑制電機(jī)垂向激勵產(chǎn)生的車輛振動負(fù)效應(yīng)，參照圖4，激勵為路面垂向位移激勵和電機(jī)垂向激振力，振動信號為車輪動載荷，初級通道為激勵到振動信號的傳遞函數(shù)，參考信號為電機(jī)垂向激振力，控制信號為主動懸架的輸出作動力，次級通道為控制信號到振動信號的傳遞函數(shù)。考慮到電機(jī)垂向波動力直接作用于車輪，根本是增大了動載荷，從而影響了動行程和垂向加速度，因此選取了車輪動載荷為控制目標(biāo)(誤差信號)。懸架主動控制前后10 km/h工況下車輛垂向振動性能指標(biāo)響應(yīng)的時域、頻域仿真結(jié)果分別如表4和圖5所示。

表4 主動懸架控制前后車輛垂向性能有效值對比

Tab.4 Effective values of vertical performances contrast between before and after controlled by active suspension

車身垂向加速度/(m·s-2)車身俯仰角加速度/(rad·s-2)車身側(cè)傾角加速度/(rad·s-2)電機(jī)激勵0．37220．35540．4639主動控制0．27220．15030．2841左后懸架動行程/m左后車輪動載荷/N電機(jī)激勵0．0037667．6667主動控制0．0029350．2777

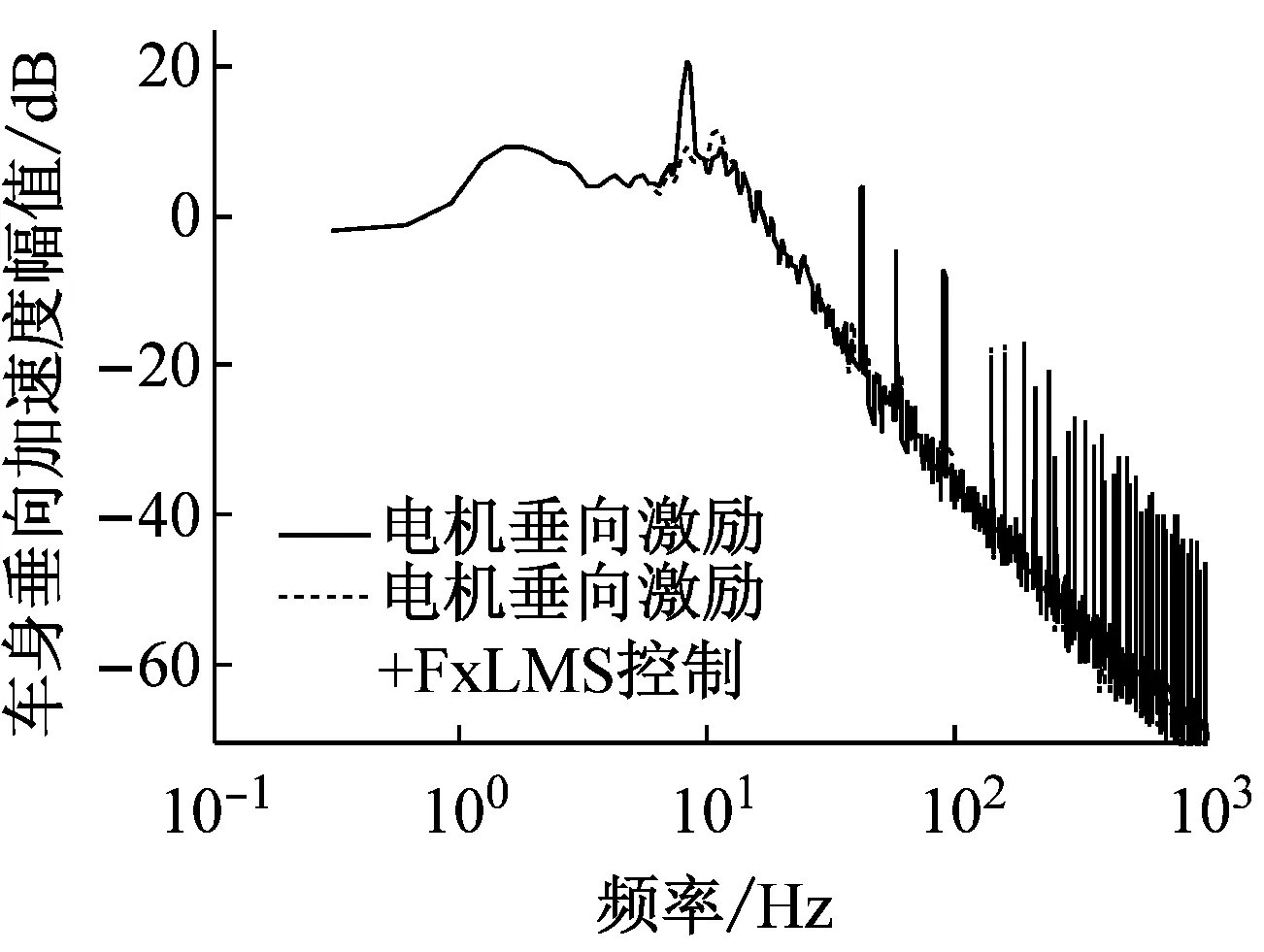
(a)

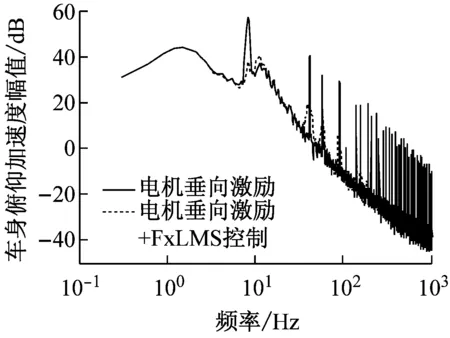
(b)

(c)

(d)

(e)

表4表明，采用基于FxLMS算法的主動懸架控制可以很好的降低車身垂向振動加速度、車身俯仰角加速度、車身側(cè)傾角加速度、懸架動行程和車輪動載荷的響應(yīng)，改善了低車速工況下SRM垂向激勵對輪邊驅(qū)動電動車垂向性能造成的負(fù)面影響，提高了車輛的平順性和操穩(wěn)性。

圖5所示的頻域分析進(jìn)一步表明，采用基于FxLMS算法的主動懸架控制能夠很好的抑制SRM垂向激勵，顯著降低了低車速工況下車身垂向振動加速度、車身俯仰角加速度、車身側(cè)傾角加速度、懸架動行程和車輪動載荷在懸架系統(tǒng)二階固有頻率處的共振響應(yīng)峰值，從而提高了車輛的平順性和操穩(wěn)性。

4 結(jié) 論

(1) 針對輪邊驅(qū)動電動車存在的輪轂電機(jī)振動問題，以開關(guān)磁阻電機(jī)為例進(jìn)行了研究。建立整車模型，討論了電機(jī)垂向激勵對后輪輪邊驅(qū)動電動車性能的影響。仿真分析表明，電機(jī)垂向激勵對車輛平順性和操穩(wěn)性的影響主要集中在低車速范圍。此時，電機(jī)激勵頻率接近懸架系統(tǒng)固有頻率，容易引起車輛共振。

(2) 鑒于電機(jī)垂向激勵具有的周期性特點，提出了基于FxLMS算法的主動懸架控制抑制其對輪邊驅(qū)動電動車平順性和操穩(wěn)性產(chǎn)生的負(fù)面影響，仿真分析驗證了方法的有效性。

[1] 寧國寶．電動車輪邊驅(qū)動系統(tǒng)的發(fā)展[J]．上海汽車，2006(11)：2-6．

NING Guobao．The development of direct wheel drives system[J]．Shanghai Auto，2006(11)：2-6．

[2] 寧國寶，萬鋼．輪邊驅(qū)動系統(tǒng)對車輛垂向性能影響的研究現(xiàn)狀[J]．汽車技術(shù)，2007(3)：21-25．

NING Guobao，WAN Gang．The present research situation of the influences on vehicle vertical performances induced by direct wheel drives system[J]．Automobile Technology，2007(3)：21-25．

[3] 褚文強，辜承林．電動車用輪轂電機(jī)研究現(xiàn)狀與發(fā)展趨勢[J]．電機(jī)控制與應(yīng)用，2007，34(4)：1-5．

CHU Wenqiang，GU Chenglin．Application status and developing tend of in-wheel motors used for electric automobile[J]．Electric Machines & Control Application，2007，34(4)：1-5．

[4] 吳建華，陳永校．開關(guān)磁阻電動機(jī)的噪聲及其抑制方法[J]．中小型電機(jī)，1997，24(3)：20-23．

WU Jianhua，CHEN Yongxiao．Acoustic noise reduction in switched reluctance Motor[J]．S & M Electric Machines，1997，24(3)：20-23．

[5] WU C Y，POLLOCK C．Time domain analysis of vibration and acoustic noise in the switched reluctance drive[C]//Sixth International Conference on Electrical Machines and Drives，Sep 8-10，1993，Oxford．IET，1993：558-563．

[6] CAMERON D E，LANG J H，UMANS S D.The origin and reduction of acoustic noise in doubly salient variable-reluctance motors[J]．IEEE Transactions on Industry Applications，1992，28(6)：1250-1255．

[7] 陳景易．開關(guān)磁阻電機(jī)徑向力的計算與分析[J]．電站系統(tǒng)工程，2012，28(3)：13-14．

CHEN Jingyi．Analysis of radial force for switched reluctance motor[J]．Power System Engineering，2012，28(3)：13-14．

[8] GARRIGAN N R，SOONG W L，STEPHENS C M，et al．Radial force characteristics of a switched reluctance machine[C]∥ Industry Applications Conference, Thirty-Fourth IAS Annual Meeting，Oct 3-7，1999，Phoenix，AZ．New York：IEEE，1999：2250-2258．

[9] SANTOS F L M，ANTHONIS J，NACLERIO F，et al．Multiphysics NVH modeling: simulation of a switched reluctance motor for an electric vehicle[J]．IEEE Transactions on Industrial Electronics，2013，61(1)：469-476．

[10] MEEK B，VAN DER AUWEAR H，DE LANGHE K．Challenges in NVH for Electric Vehicles[C]∥ Proceedings of the FISITA 2012 World Automotive Congress，Nov 27-30，Beijing，china．Berlin Heidelberg：Springer-Verlag，2013：675-685．

[11] INDERKA R B，DE DONCKER R W．High dynamic direct average torque control for switched reluctance drives[C]∥Industry Applications Conference, Thirty-Sixth IAS Annual Meeting，Sept 30-Oct 4，2001，Chicago，USA．New York：IEEE，2001：2111-2115．

[12] XUE X D，CHENG K W E，HO S L，et al．A drivetrain scheme of electric vehicles using switched reluctance motors with torque ripple reduction[C]∥8th International Conference on Advances in Power System Control, Operation and Management，Nov 8-11，2009，Hong Kong，China．IET，2009：1-6．

[13] 楊波，曹家勇，陳幼平．一種降低開關(guān)磁阻電機(jī)轉(zhuǎn)矩脈動的新方法[J]．中小型電機(jī)，2001，28(4)：12-16．

YANG Bo，CAO Jiayong，CHEN Youping．A new method of torque ripple reducing for switched reluctance motor[J]．S & M Electric Machines，2001，28(4)：12-16．

[14] 張義民，薛玉春，賀向東．基于開關(guān)磁阻電機(jī)驅(qū)動系統(tǒng)的電動汽車振動研究[J]．汽車工程，2007，29(1)：46-49．

ZHANG Yimin，XUE Yuchun，HE Xiangdong．A research on the vibration of an electric vehicle using switched reluctance motor as drive system[J]．Automotive Engineering，2007，29(1)：46-49．

[15] 盧少波．汽車底盤關(guān)鍵子系統(tǒng)及其綜合控制策略研究[D]．重慶：重慶大學(xué)，2009．

[16] PAVITHRA S，NARASIMHAN S V．Feedback active noise control based on forward-backward LMS predictor[J]．Signal Image and Video Processing，2013，7(6)：1083-1091．

[17] 張鋒，李以農(nóng)，丁慶中. FxLMS算法的實驗及硬件在環(huán)仿真驗證[J].重慶大學(xué)學(xué)報，2013，3(8)：26-32.

ZHANG Feng, LI Yinong, DING Qingzhong. FxLMS algorithm’s realization and verification by hardware in the loop simulation[J]. Journal of Chongqing University, 2013, 3(8):26-32.

[18] 丁慶中，李以農(nóng)，張鋒,等. 基于自適應(yīng)濾波算法的齒輪傳動系統(tǒng)振動主動控制[J].機(jī)械工程學(xué)報，2013，49(15)：74-81.

DING Qingzhong, LI Yinong, ZHANG Feng, et al. Adaptive filter algorithm for active vibration control of gear transmission[J]. Journal of Mechanical Engineering, 2013，49(15)：74-81.

Vertical vibration of in-wheel motor electric vehicles based on active suspension control

ZHONG Yinhui2, LI Yinong1,2, YANG Chao2, XU Guanghui2, MENG Fanming1

(1.State Key Lab. of Mechanical Transmission， Chongqing University， Chongqing 400030， China; 2. School of Automotive Engineering, Chongqing University, Chongqing 400030, China)

Aiming at the hub motor’s vibration problem of an in-wheel motor electric vehicle(IWM-EV), the switched reluctance motor (SRM) was taken as an example, the effects of the motor’s vertical excitation on the dynamic performance of the vehicle were analyzed. Under conditions of different vehicle speeds, the effects of the coupling between road surface excitation and the motor’s one on the vertical dynamic performance of the vehicle were explored. The study results showed that the effects of the motor’s excitation on the vehicle’s vertical dynamic performance are concentrated in a lower speed range. Due to the periodic feature of SRM excitation, the active suspension control method based on the FxLMS algorithm was proposed to suppress the vehicle’s vertical vibration responses excited by SRM excitation. The simulation results verified the effectiveness of this method.

in-wheel motor; switched reluctance motor; vertical excitation and response; FxLMS algorithm

國家自然科學(xué)基金(51275541)；中央高校基本科研業(yè)務(wù)費資助(106112015CDJZR118805)

2016-01-21 修改稿收到日期：2016-03-31

鐘銀輝 男，博士生，1981年生。

李以農(nóng) 男，博士，教授,博士生導(dǎo)師，1961年生，E-mail:ynli@cqu.edu.cn。

U469.72

A

10.13465/j.cnki.jvs.2017.11.037