小波變換在火箭遙測數據誤碼剔除中的應用

柳振民，彭宗堯，郭力聞

(西昌衛星發射中心， 四川 西昌 615000)

【信息科學與控制工程】

小波變換在火箭遙測數據誤碼剔除中的應用

柳振民，彭宗堯，郭力聞

(西昌衛星發射中心， 四川 西昌 615000)

利用MATLAB 仿真，對兩段具有代表性的火箭飛行遙測數據進行了小波變換。通過分析不同小波基、分解層數和閾值規則下的處理效果，研究利用小波變換剔除火箭遙測數據誤碼的可行性。結果表明:對于同一表現形式的遙測數據，只要選擇合適的小波基和分解層數，利用小波交換可有效剔除數據中所含誤碼。

遙測數據誤碼；小波變換；均方誤差；平滑度指標

火箭在測試及飛行過程中，主要依據遙測數據掌握其健康狀況。近年來，火箭發射頻率越來越高，而人工分析大量遙測數據效率低，不能滿足火箭高密度發射需求，因此需實現遙測數據的自動分析。由于火箭測試、飛行環境復雜，遙測信號在接收過程中受到各種干擾，一些大的干擾在信號的接收解調環節無法被濾除，以誤碼的形式摻雜在遙測數據之中。實際情況表明，誤碼占數據的比率不大，但卻嚴重影響數據的分析結果。為真實掌握火箭的健康狀況，在數據自動分析的第一個環節，必須對遙測數據中所含誤碼進行剔除。

目前采用的設置上下值剔除法、分段設置上下值剔除法兩種誤碼剔除方法對折線型和曲線型數據不適用，且在剔除直線型和臺階型數據所含的誤碼時，經常將反映真實異常現象的有用數據剔除。小波變換可根據實際分析的需要，自動調節時間窗和頻率窗[1]，在低頻部分具有較高的頻率分辨率和較低的時間分辨率，在高頻部分具有較高的時間分辨率和較低的頻率分辨率，從而能在濾除跳變的同時較好地保持數據的原樣性，因而比較適合用于剔除火箭遙測數據中的誤碼。

1 誤碼特性及影響分析

火箭遙測數據中所含的誤碼主要來源于信號接收時受到的較大干擾，如測試期間天線附近的人員走動、飛行期間級間分離火焰的干擾等。一般情況下，誤碼在火箭遙測數據中比率不高，且常表現為不符合物理規律的突然跳動。圖1為火箭某一遙測壓力參數(含誤碼)，在1600多個數據中，誤碼的數量只有6個；另外該參數不可能在短時間內突然升高或降低，但誤碼處的數據則表現為突然上跳或下跳。

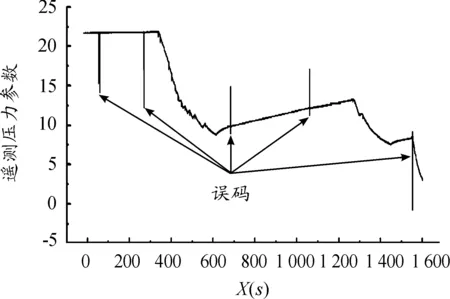
圖1 火箭某一遙測壓力參數曲線

在人工對火箭遙測數據進行分析時，工作人員可以根據經驗判定哪些是誤碼，哪些是正常或異常數據，進而確定設備的工作狀態；在用軟件實現自動分析時，若不先對誤碼進行剔除，計算機會將含誤碼的數據判定為異常，并誤以為設備工作異常，從而使自動分析結果失去意義。

2 小波變換剔除誤碼原理

2.1 小波變換基本原理

若函數φ(t)滿足可容許性條件[2]

(1)

則稱其為母小波函數(MotherWaveletFunction)。式(1)中ψ(ω)為φ(t)的傅里葉變換。把式(1)中母小波函數φ(t)伸縮或者平移，得到小波基φa,b(t)

(2)

式(2)中：a為伸縮因子(也稱尺度因子)；b為平移因子；φa,b(t) 為依賴于α、b的小波基函數。

將式(2)中小波基的伸縮因子α按冪級數進行離散化，取α=2j(j>0的整數)，b進行均勻離散化，則序列f(t)的離散小波變換[3]為

(3)

2.2 剔除誤碼原理

如式(3)所示，將含有誤碼的數據序列f(t)在離散化的小波基下展開，然后根據誤碼的突然跳變與正常數據的變化規律在不同小波尺度上具有的不同特點，將誤碼跳變產生的分量去掉，并用剩余分量重構還原數據[4]。如圖2所示，將含有誤碼的數據f(t)進行第一層小波變換，分解成低頻CA1和高頻CD1兩種成分，正常數據包含在CA1中，但其內仍可能含有誤碼，所以再進行第2層、第3層等小波分解[5-6]。分解后誤碼主要集中在CD1、CD2、CD3等高頻小波系數中，此時可以對高頻小波系數進行處理,然后對數據f(t)進行重構，即可以達到剔除誤碼的目的。

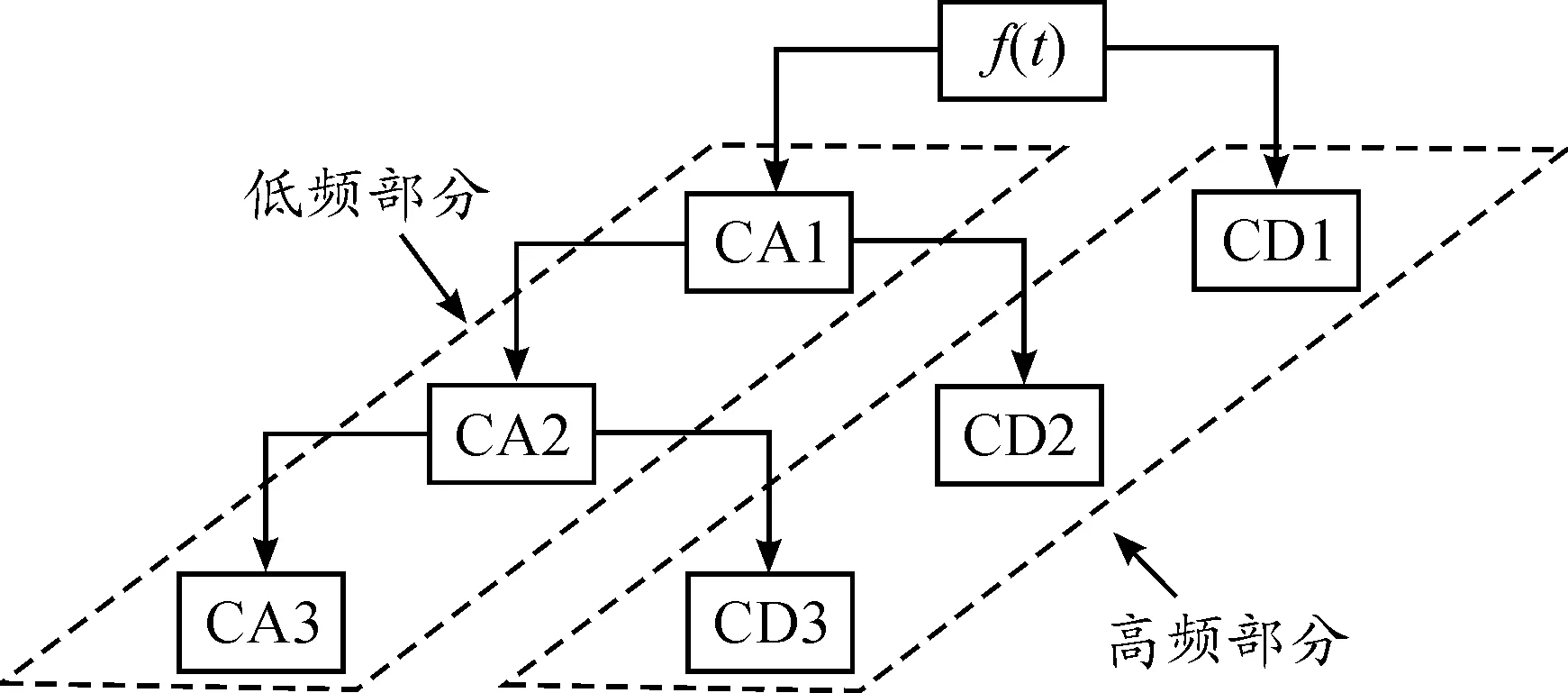
圖2 小波分解樹(3級分解)

3 遙測數據誤碼剔除Matlab實現

火箭遙測參數包括電壓，電流、壓力、溫度等類型，表現形式有直線型、臺階型、折線型、曲線型，采樣率分1 Hz和40 Hz兩種；同一參數在不用測試發射任務中表現形式基本一致。根據上述特點，本節選取兩段具有代表性的火箭飛行遙測數據，一段為采樣率40 Hz的直線型數據(B_Data_40)，一段為采樣率1 Hz的曲線型數據(C_Data_1)，兩段數據在接收過程中均受到干擾，含有誤碼。利用小波變換對兩段數據進行誤碼剔除，通過比較均方誤差(MSE)評估數據的變異程度，通過對比平滑度指標(r)分析誤碼的剔除情況，進而為兩段數據的小波變換選取最佳小波基、分解層數和閾值規則。

本文中均方誤差MSE定義為

(4)

平滑度指標r定義為[9]

(5)

式中：f(k)為手動剔除誤碼后的數據；fd(k)為小波分析剔除誤碼后的數據。

3.1 小波基選取

不同的應用領域選取不同特性的小波基。考慮到本文所要分析的遙測數據為采樣率40Hz的直線型序列數據和采樣率1Hz的曲線型序列數據，本節選取具有良好正交性和對稱性[7]的Daubechies、Symlets和Coiflet3種離散小波進行比較分析[8]。

為減少分析的樣本，本節統一使用Stein無偏似然估計閾值(rigrsure)規則，利用不同的小波基，對采樣頻率為40Hz的直線型數據進行5層分解，對采樣頻率為1Hz的曲線型數據進行3層分解，分析結果如表1、表2所示。表中dbN為Daubechies的表示形式，symN為Symlets的表示形式，coifN為Coiflet的表示形式，N為小波的階數，粗體數字為剔除誤碼效果較好的指標。

表1 B_Data_40數據分析結果(五層分解)

對表1中統計的均方誤差(MSE)和平滑度指標(r)進行比較，可以看出利用dbN、symN、coifN 3種小波剔除B_Data_40數據誤碼時，整體上dbN小波的效果最好，symN小波次之，coifN小波最差；不同的小波階數效果也不同，就單個小波基而言，sym7效果最好。

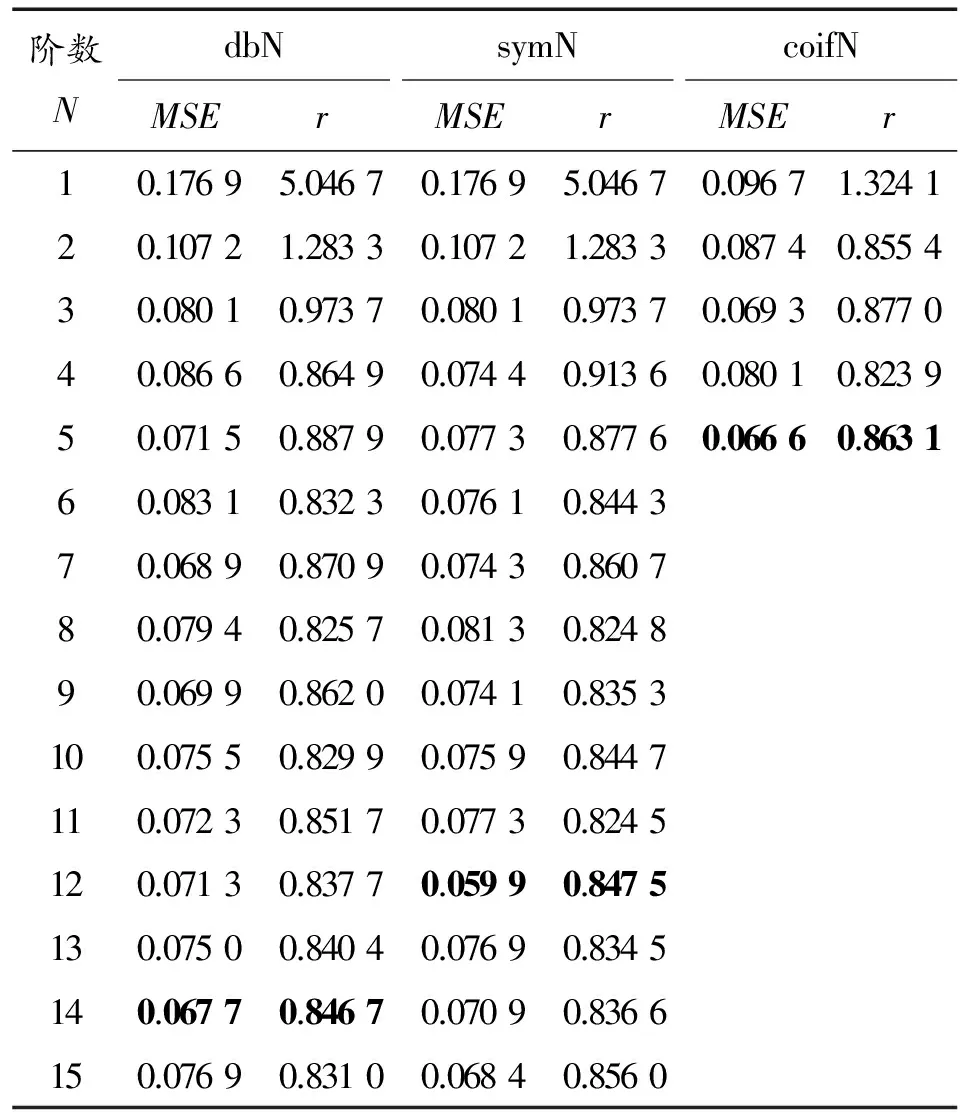
表2 C_Data_1數據分析結果(3層分解)

從表2的統計情況來看，利用dbN、symN、coifN3種小波剔除C_Data_1數據誤碼時效果無明顯差異；不同的小波階數效果也不同，單個小波基而言，sym12效果最好。

3.2 分解層數確定

根據上節分析的結果，分別用sym7小波基對B_Data_40數據、sym12小波基對C_Data_1數據進行各層分解，用均方誤差(MSE)、平滑度指標(r)來評估各分解層數的效果，分析的結果如表3所示。

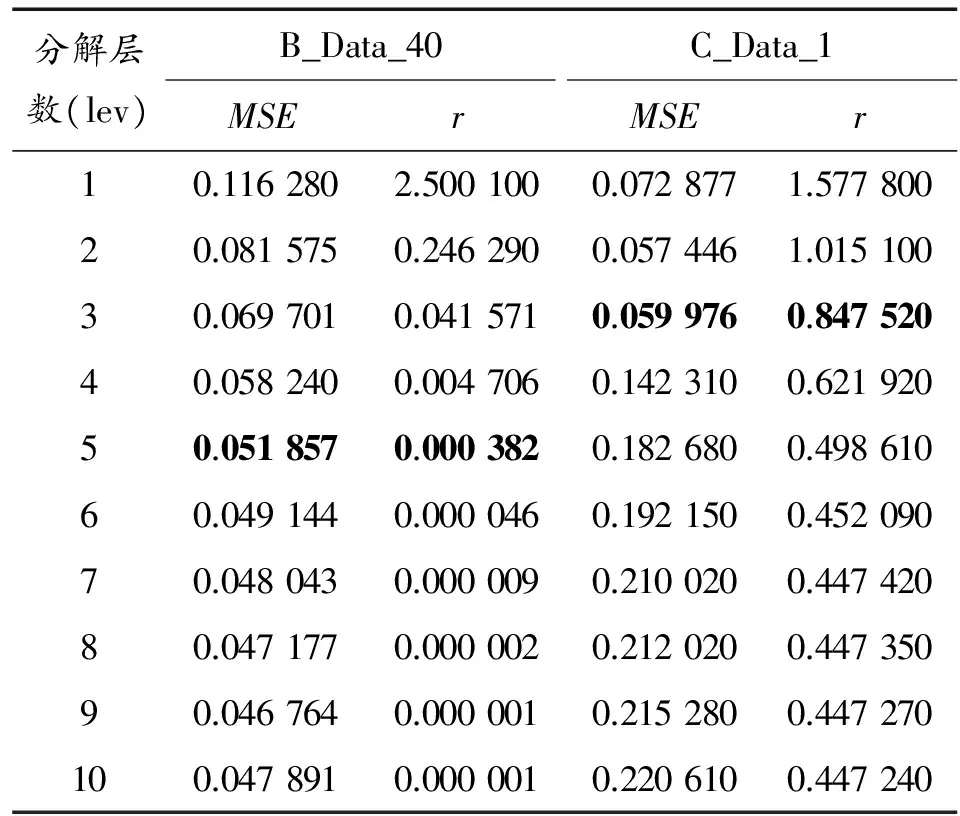
表3 不同分解層數數據分析結果

從表3可以看出，分解層數對于消除誤碼的效果影響很大。對B_Data_40數據進行前5層分解時，隨分解層數的增加均方誤差(MSE)和平滑度(r)均越來越好，5層以后的變化不太明顯；對C_Data_1數據進行前4層分解時，隨分解層數的增加效果逐漸變好，4層以后的分解效果反而越來越差。

分析結果表明，過多的分解層數會使數據中真實信息丟失，引起數據變異，且導致運算量增大,因此在滿足誤碼剔除要求后，盡量選擇較低的分解層數。

3.3 閾值規則選擇

根據以上兩節的分析結果，分別利用固定閾值(sqtwolog)、Stein無偏似然估計閾值(rigrsure)、啟發式閾值(heursure)、極大極小閾值(minimaxi)4種閾值規則[10]，對B_Data_40數據使用sym7小波基進行5次分解，對C_Data_1數據使用sym12小波基進行3次分解，比較其處理效果，以選擇最佳的閾值規則。處理的結果如表4及圖3、圖4所示。從表4得知，利用4種閾值規則計算出的均方誤差(MSE)和平滑度指標(r)相同；從圖3、圖4看出，不同的閾值規則均能較好地剔除數據中的誤碼。由此可以得出：不同的閾值規則對數據的小波變換結果影響不大。

以上分析結果表明，在4種閾值規則的任一規則下，對B_Data_40數據使用sym7小波基進行5層分解，對C_Data_1數據使用sym12小波基進行3層分解(效果如圖3、圖4所示)，既可剔除數據中所含的誤碼，又未引起數據較大的變異(MSE<0.06)，滿足遙測數據誤碼剔除的要求。

圖3 B_Data_40數據處理結果

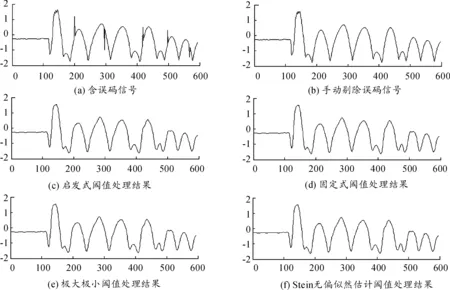
圖4 C_Data_1數據處理結果

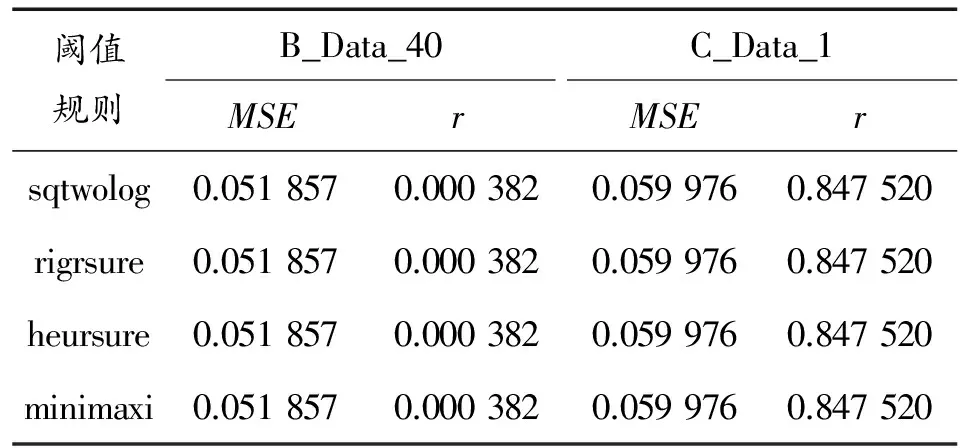
閾值規則B＿Data＿40MSErC＿Data＿1MSErsqtwolog0．0518570．0003820．0599760．847520rigrsure0．0518570．0003820．0599760．847520heursure0．0518570．0003820．0599760．847520minimaxi0．0518570．0003820．0599760．847520

4 結束語

本文基于小波變換理論，嘗試將小波變換應用于火箭遙測數據誤碼剔除的可行性。通過對兩段具有代表性的火箭遙測數據進行小波變換可以看出：在利用小波變換剔除遙測數據誤碼時，對于同一表現形式的數據，只要選擇合適的小波基和分解層數，就能較好地剔除數據中所含誤碼。在后續的實際應用中，還需對火箭遙測數據按表現形式和采樣率進行分類，并在同類別中選出具有代表性的數據進行小波變換，通過比較均方誤差(MSE)和平滑度指標(r)選出該類數據最佳的小波基和分解層數；另外，在滿足誤碼剔除要求后，盡量選擇較低的分解層數，確保在實際應用過程中，既剔除誤碼，又減少運算量，且盡量不引起數據變異。

[1] 魏思維,黃玉平,鄭華義.小波變換在伺服系統信號處理中的應用研究[J].現代防御技術,2013(6):170-175.

[2]STEPHANEMALLAT.信號處理的小波引導[M].楊力華,戴道清,譯.北京:機械工業出版社,2002.

[3] 劉志松.基于小波分析的信號去噪方法[J].浙江海洋學院學報(自然科學版),2011(2):150-154.

[4] 高成文,吳健華.遙測非平穩信號小波閾值降噪方法的改進及仿真[J].電子測量技術,2013 (15):62-64.[5] 王正林.精通MATLAB7[M].北京:電子工業出版社,2007.

[6] 葛哲學,陳仲生.MATLAB時頻分析技術及其應用[M].北京:人民郵電出版社,2006.

[7] 高彩紅,李天博,錢坤喜,等.基于MATLAB的心電去噪中小波基選取研究[J].微計算機信息,2010,(19):222-223.

[8] 唐曉初.小波分析及應用[M].重慶:重慶大學出版社,2006:58-70.

[9] 張春蕾.小波變換在GPS變形監測中的應用[D].武漢:武漢大學,2007.

[10]林淵,肖鋒,鄭賓,等.小波變換閾值降噪方法及在武器自動機數據處理中的應用[J].電子測量技術,2009,(1):128-130.

[11]焦新泉，李功，侯卓，等.基于電容式噪聲傳感器的信號調理電路設計[J].火力與指揮控制，2016(10)：159-162.

(責任編輯 楊繼森)

Application of Wavelet Transform in Eliminating Error of Rocket Telemetry Data

LIU Zhen-min, PENG Zong-yao, GUO Li-wen

(Xichang Satellite Launch Center, Xichang 615000, China)

Using MATLAB simulation，we did wavelet transform to the two segment of the representative rocket telemetry data. By comparing the effects that using the different wavelet base, decomposition level and threshold rule, we studied whether the method of using wavelet transform to eliminate the error of rocket telemetry data is feasible. The results show that for the same form of telemetry data, if use the appropriate wavelet base and decomposition level, using wavelet transform can effectively eliminate the error in the data.

error in rocket telemetry data; wavelet transform; mean square error; smoothness index

2016-12-27；

2017-01-23 基金項目：火箭測試數據智能分析系統項目(2016SY27A0019) 作者簡介：柳振民(1980—)，男，碩士，工程師，主要從事火箭測試發射及數據分析。

10.11809/scbgxb2017.05.021

format:LIU Zhen-min, PENG Zong-yao, GUO Li-wen.Application of Wavelet Transform in Eliminating Error of Rocket Telemetry Data[J].Journal of Ordnance Equipment Engineering,2017(5):94-98.

TJ7；TP3

A

2096-2304(2017)05-0094-05

本文引用格式：柳振民，彭宗堯，郭力聞.小波變換在火箭遙測數據誤碼剔除中的應用[J].兵器裝備工程學報，2017(5):94-98.