改進(jìn)型圓面陣的快速波束形成算法設(shè)計(jì)
于滌非, 張春華, 黃勇
(中國科學(xué)院大學(xué), 北京 100190)
?
改進(jìn)型圓面陣的快速波束形成算法設(shè)計(jì)
于滌非, 張春華, 黃勇
(中國科學(xué)院大學(xué), 北京 100190)
為降低基于圓面陣的三維成像聲納波束形成算法的運(yùn)算量,提出改進(jìn)圓面陣布陣陣型設(shè)計(jì)及優(yōu)化波束方位的方法。改進(jìn)型圓面陣由多條通過圓心的線陣組成,其波束形成等效于所有線陣波束形成結(jié)果的疊加;通過對波束方位進(jìn)行優(yōu)化,使得每一條線陣的波束形成過程等效為等長度的一維快速傅里葉變換運(yùn)算。仿真結(jié)果表明,改進(jìn)型圓面陣的波束形成運(yùn)算量較直接計(jì)算顯著降低。運(yùn)用改進(jìn)型圓面陣可顯著降低三維成像聲納信號處理系統(tǒng)的復(fù)雜度,提高了聲納的綜合性能。
聲學(xué); 三維成像聲納; 圓面陣; 波束形成; 快速傅里葉變換
0 引言
近年來,利用平面換能器陣通過波束形成對水下目標(biāo)進(jìn)行三維成像技術(shù)發(fā)展迅速。實(shí)時三維成像聲納[1-6]常用的平面基陣為方陣[1-3]、同心圓面陣[2-6]等。
基于方陣的三維成像聲納的優(yōu)點(diǎn)是存在大量快速波束形成算法,能夠運(yùn)用快速傅里葉變換(FFT)[2]或Chirp z變換(CZT)[7]等方法降低運(yùn)算量。可以采用編程方便靈活的數(shù)字信號處理器(DSP)實(shí)現(xiàn)其信號處理系統(tǒng)[8]。但也存在一定的缺點(diǎn),在基陣陣元數(shù)一定的情況下,聲納的視場范圍與測向精度是一對矛盾。為提高測向精度,需要增加陣元間距以擴(kuò)大基陣孔徑,而陣元間距的增加會縮小視場范圍。如果同時提高測向精度和視場范圍,則必須大量增加基陣陣元數(shù),從而增加系統(tǒng)復(fù)雜度。
基于同心圓面陣的三維成像聲納在一定程度上可以解決視場范圍與測向精度間的矛盾。同心圓面陣陣元間距大于半波長時,其波束方向圖上不會出現(xiàn)柵瓣[4],因此在陣元數(shù)一定的條件下,聲納可以同時獲得較大的視場范圍與較高的測向精度。但基于同心圓面陣的三維成像聲納同樣有一定的缺點(diǎn),文獻(xiàn)[9]指出圓面陣的波束形成可等效為廣義傅里葉變換,運(yùn)算量較大,且無法通過FFT、CZT等方法降低運(yùn)算量,因此對于基于同心圓面陣的三維成像聲納,其信號處理系統(tǒng)較為復(fù)雜,一般只能采用圖形處理器(GPU)[10]或現(xiàn)場可編程門陣列(FPGA)[11]實(shí)現(xiàn)。其實(shí)現(xiàn)難度較大,靈活性較差。
因此,三維成像聲納設(shè)計(jì)時很難兼顧視場范圍、測向精度、運(yùn)算量、陣元數(shù)這4方面的性能,一般都需要犧牲某些方面的性能以保證主要指標(biāo)滿足設(shè)計(jì)要求。為解決上述問題,本文提出一種改進(jìn)型圓面陣設(shè)計(jì),基于該圓面陣的三維成像聲納能夠兼顧這4方面的性能,從而提高聲納整體性能。
1 基于同心圓面陣三維成像聲納的特點(diǎn)
假設(shè)布陣間距為d,聲納發(fā)射單頻脈沖信號,波長為λ,使用如圖1所示的俯仰角θ及方位角φ定義。

圖1 聲納方位角及俯仰角定義Fig.1 Definition of azimuth and elevatioan angle of sonar
文獻(xiàn)[1]中采用半波長布陣的正方形柵格圓面陣,視場范圍為θ∈[0°,90°],φ∈[0°,360°],陣元數(shù)為3 136,角分辨率為1.6°. 文獻(xiàn)[2]中采用波長布陣的方陣,角分辨率為1°,陣元數(shù)為2 304,視場范圍為θ∈[0°,30°],φ∈[0°,360°]. 波長布陣相比于半波長布陣可以獲得更高的測向精度,但視場范圍有所降低。
同心圓面陣相比于方陣的優(yōu)點(diǎn)是可以在陣元數(shù)基本不變的條件下,同時提高角分辨率及視場范圍。
對比文獻(xiàn)[2]中的方陣,如果采用陣元數(shù)基本相同的同心圓面陣,則在波長布陣時,其角分辨率為0.93°,視場范圍為θ∈[0°,90°],φ∈[0°,360°].
同心圓面陣上,所有的陣元均分布在同心圓環(huán)上,相鄰圓環(huán)的半徑差為布陣間距d;每個圓環(huán)上,陣元均勻分布,陣元間距同樣為d. 一個具有2 362陣元,布陣間距等于波長的同心圓面陣陣型如圖2所示。

圖2 同心圓面陣陣型Fig.2 Concentric circular array
遠(yuǎn)場條件下,基于圖2的三維成像聲納對位于θ=30°、φ=180°的點(diǎn)目標(biāo)成像的波束方向圖在sinφ=0切片上與方陣的結(jié)果對比如圖3所示。

圖3 同心圓面陣與方陣波束方向圖對比Fig.3 Comparison of beam pattern of concentric circular array and square array
方陣的波束方向圖在θ=30°、φ=0°出現(xiàn)柵瓣,而同心圓面陣的結(jié)果沒有出現(xiàn)柵瓣,位于θ=30°、φ=0°的波束高度為-15.21 dB. 因此同心圓面陣的視場范圍可以達(dá)到θ∈[0°,90°],φ∈[0°,360°]. 表1為3種陣型的比較。

表1 不同陣型性能比較Tab.1 Comparison of performances of different arrays
圖4為同心圓面陣在視場范圍內(nèi)對該點(diǎn)目標(biāo)成像的波束方向圖。
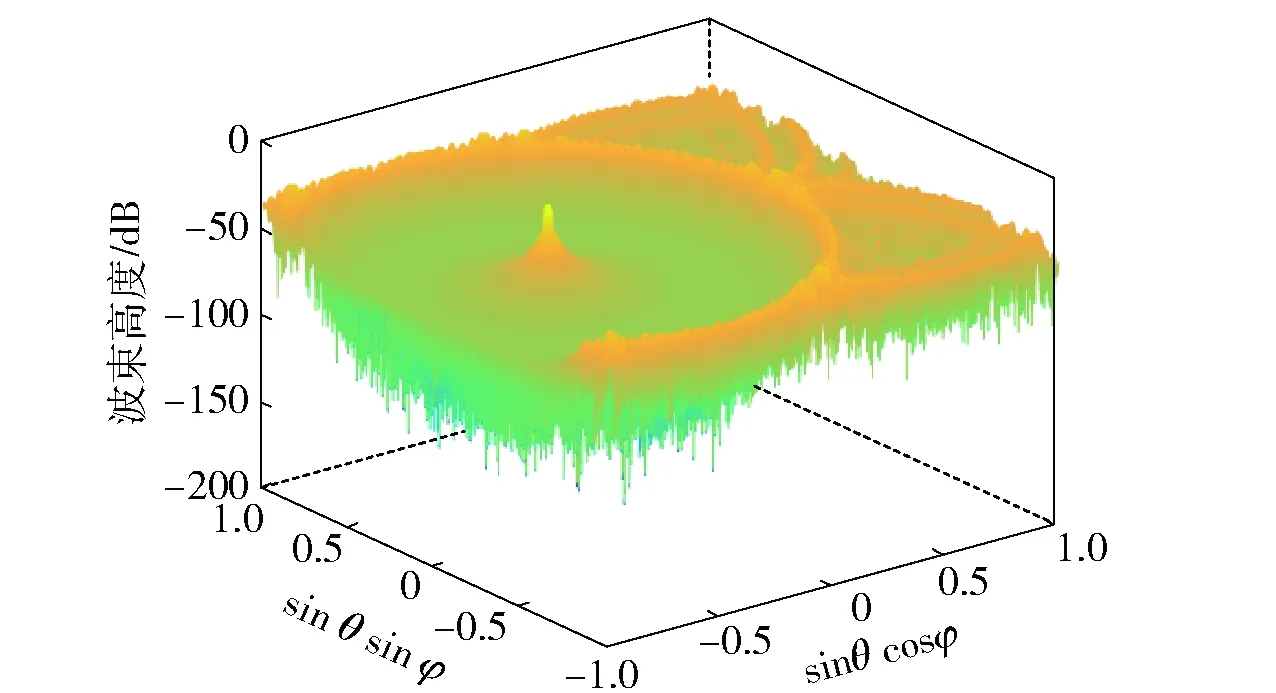
圖4 同心圓面陣對點(diǎn)目標(biāo)成像的波束方向圖Fig.4 Beam pattern of point target imaged by concentric circular array
方陣[2]要同時達(dá)到角分辨率為1°,視場范圍為θ∈[0°,90°],φ∈[0°,360°],則基陣陣元數(shù)需要增加至9 216陣元。這不僅增加了系統(tǒng)復(fù)雜度,同時由于布陣間距減小,基陣陣子的直徑也同時減小,其內(nèi)阻增加[12],會導(dǎo)致數(shù)據(jù)采集系統(tǒng)輸出信號的信噪比降低。
基于同心圓面陣的三維成像聲納則可以在陣元數(shù)一定的條件下,同時提高角分辨率及視場范圍。
但同心圓面陣的波束形成無法采用FFT運(yùn)算降低運(yùn)算量,其波束形成實(shí)現(xiàn)一般只能采用編程復(fù)雜、靈活性較差的GPU或FPGA,不適合使用DSP. 如果能對同心圓面陣進(jìn)行改進(jìn),使得改進(jìn)型圓面陣可以使用FFT算法降低運(yùn)算量,則可以在提高三維成像聲納性能的同時降低算法的實(shí)現(xiàn)難度。
2 圓面陣陣型設(shè)計(jì)
方陣、六角形陣等陣型之所以存在頻域FFT波束形成[9],是因?yàn)檫@兩種陣型均可以通過線陣拓?fù)涞玫健H绻O(shè)計(jì)一種圓面陣,其陣型同樣可以通過線陣拓?fù)涞玫剑瑒t該圓面陣也可以通過FFT運(yùn)算降低運(yùn)算量。
文獻(xiàn)[13]中給出一種可以通過線陣拓?fù)涞玫降膱A面陣,組成圓面陣的每一條線陣為均勻線陣且均不是稀疏的。如果按照這種方式構(gòu)造圓面陣,則在基陣孔徑一定的情況下,基陣只能集成很少的陣元,陣增益較低,不適合三維成像聲納。對這種設(shè)計(jì)方式進(jìn)行改進(jìn),使設(shè)計(jì)的圓面陣滿足三維成像聲納的應(yīng)用需求。
三維成像聲納設(shè)計(jì)時,一般會根據(jù)性能指標(biāo)要求、加工工藝水平、電路規(guī)模等限制條件確定聲納基陣能夠集成的陣元數(shù)及陣元間距。因此改進(jìn)型圓面陣的設(shè)計(jì)目標(biāo)是在給定陣元間距d以及給定基陣的期望陣元數(shù)Ke條件下,設(shè)計(jì)一種圓面陣滿足:
1) 圓面陣上任意相鄰兩個陣元間距不小于d;
2) 圓面陣的陣元數(shù)盡可能接近Ke;
3) 圓面陣由同心圓環(huán)陣構(gòu)成,同時可由線陣拓?fù)涠桑?/p>
4) 盡可能降低基陣孔徑,即陣元間距盡可能接近d.
基于如上要求設(shè)計(jì)的圓面陣,可以在陣元數(shù)一定的條件下盡可能減小基陣面積,從而降低聲納的體積。
為達(dá)到設(shè)計(jì)要求,按照如下方式構(gòu)造面陣:
1) 假設(shè)圓面陣的層數(shù)M=3(中心陣元不算做一層),即圓面陣由M個同心圓環(huán)陣組成,第m層圓環(huán)陣半徑為md;
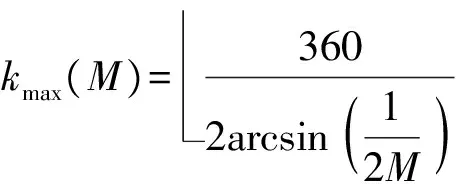
kmax(M)=3602arcsin(12M)
2) 計(jì)算第M層圓環(huán)陣陣元間距為d時能容納的最多陣元數(shù)

,其中?」表示向下取整。初始化搜索過程中的最外層陣元數(shù)變化量Θ=0;
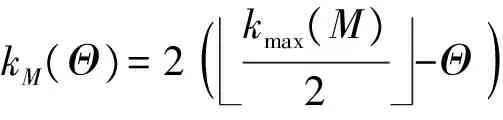
kM(Θ)=2(kmax(M)2-Θ)
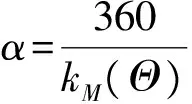

αm=2arcsin(12m)α
4) 令m=m-1,計(jì)算第m層圓環(huán)陣相鄰兩個陣元方向向量夾角


Km(Θ)=360αm
α,「?表示向上取整,即第m層圓環(huán)陣相鄰兩個陣元方向向量夾角必然為α的整數(shù)倍。第m層圓陣的陣元數(shù)為

;


Θ=kmax(M)22
6) 令Θ=Θ+1,回到第3步,統(tǒng)計(jì)并記錄K(M,Θ),直至;
7) 求取K(M,Θ)的最大值K(M,Θmax),則K(M,Θmax)即為當(dāng)圓面陣層數(shù)為M時,能夠容納的最多陣元數(shù);
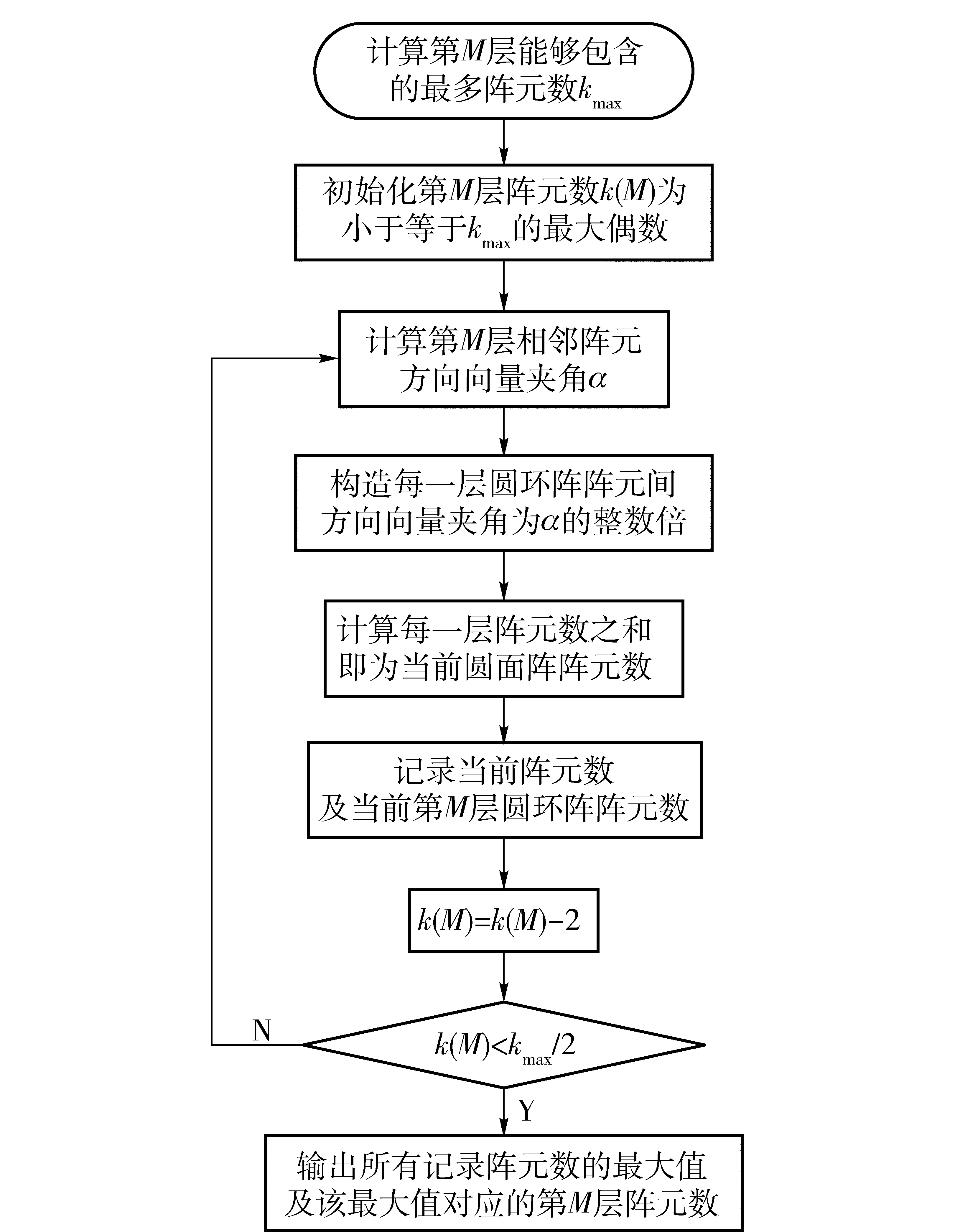
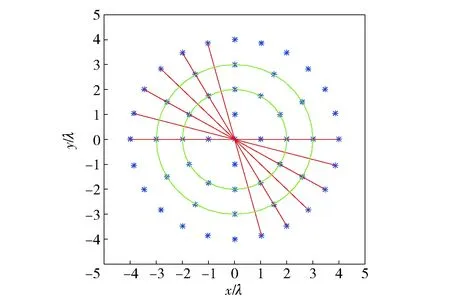
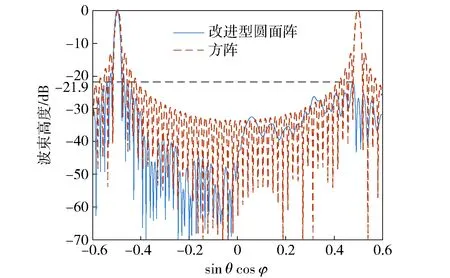
8) 如果K(M,Θmax)≥Ke,則M即為圓面陣層數(shù),Θmax對應(yīng)的kM(Θ)即為圓面陣最外層陣元數(shù),該圓面陣已滿足設(shè)計(jì)要求,搜索過程結(jié)束。如果K(M,Θmax) 按照以上步驟構(gòu)造的圓面陣,是陣元數(shù)量大于Ke且最接近Ke的圓面陣,且在該數(shù)量下做到了孔徑最小,圖5為搜索圓面陣層數(shù)流程圖。 圖5 圓面陣層數(shù)搜索流程圖Fig.5 Flow chart of layer number searching of improved circular array 圖6為計(jì)算層數(shù)為M的圓面陣能容納陣元數(shù)量最大值的算法流程圖。 圖6 層數(shù)為M的圓面陣最大陣元數(shù)搜索流程圖Fig.6 Flow chart of maximum sensor number searching of M-layer improved circular array 構(gòu)造過程實(shí)際是兩個嵌套的窮舉過程,首先從圓面陣可能的最小層數(shù)開始,計(jì)算圓面陣能夠包含的最多陣元數(shù)。如果陣元數(shù)大于期望陣元數(shù)Ke,則可以確定使得圓面陣陣元數(shù)大于Ke的最小層數(shù)。 在計(jì)算層數(shù)為M的圓面陣能夠容納陣元數(shù)的最大值時,首先根據(jù)陣元間距計(jì)算第M層最多陣元數(shù),窮舉第M層陣元數(shù)為大于最多陣元數(shù)一半的所有偶數(shù)。計(jì)算對應(yīng)的圓面陣能夠包含的陣元數(shù),陣元數(shù)最大值即為層數(shù)為M的圓面陣至多能包含的陣元數(shù)。這樣構(gòu)造的圓面陣,由層數(shù)及最外層陣元數(shù)唯一確定。 改進(jìn)型圓面陣上,位于同一圓環(huán)陣上的相鄰兩個陣元方向向量夾角均為α的整數(shù)倍。假設(shè)圓面陣中心陣元位于圓面陣坐標(biāo)系原點(diǎn),則圓面陣可以看做由L=KM(Θmax)/2條穿過坐標(biāo)原點(diǎn)的線陣組成。因此該圓面陣可以分解為多個圓環(huán)陣,相鄰圓陣的半徑差為d,也可以分解為多個稀疏線陣,線陣相鄰兩個陣元間距必然為d的整數(shù)倍。 圖7 改進(jìn)型圓面陣實(shí)例Fig.7 Example of improved circular array 圖7為Ke=48的圓面陣。該圓面陣包含53個陣元,共4層,可以分解為4個等間距圓環(huán)陣,同時可以分解為12條線陣,每條線陣相鄰陣元間距為d的整數(shù)倍。 圖7所示的圓面陣,是由12條線陣等角度旋轉(zhuǎn)拓?fù)涠伞R虼嗽搱A面陣在波束形成時,等效為12條線陣波束形成結(jié)果的線性疊加。球坐標(biāo)系下,層數(shù)為M,最外層陣元數(shù)為2L的改進(jìn)型圓面陣在發(fā)射單頻矩形信號時[2]的遠(yuǎn)場波束形成公式為 B(u)= (1) 式中:ωln為第l條線陣上、第n個陣元的權(quán)重,如果該位置沒有陣元,則權(quán)重為0;Sln為該陣元收到的信號經(jīng)解調(diào)后得到的復(fù)信號;u=(ux,uy,uz)=(sinθcosφ, sinθsinφ, cosθ)為波束的單位方向矢量。 由三角函數(shù)公式,(1)式可化為 (2) 令 (3) (3) 式表示第l條線陣的波束形成過程。因此改進(jìn)型圓面陣的波束形成過程,等效為L條線陣波束形成結(jié)果的線性疊加。 由于組成改進(jìn)型圓面陣的每一條線陣均是對一個陣元間距為d的均勻線陣的稀疏抽取,因此只要合理地選取波束方向[9],就可以使用一維FFT運(yùn)算來計(jì)算每一條線陣的波束方向圖,從而降低計(jì)算量。 由于組成圓面陣的線陣不是平行的,而是等角度旋轉(zhuǎn)而形成的,如果波束方向選取不合理,會造成不同線陣在波束形成時,其FFT的長度不同,F(xiàn)FT長度越長,計(jì)算量越大。為獲得最低計(jì)算量,需要設(shè)計(jì)一種波束方向圖的波束分布方式,滿足如下兩個條件: 1)可以使用一次一維FFT運(yùn)算來計(jì)算每一條線陣的波束形成過程; 2)組成圓面陣的每一條線陣波束形成時,所對應(yīng)的一維FFT運(yùn)算長度相等。 對于(3)式,假如存在整數(shù)k、Nl,使得 (4) 則(3)式可化為 因此當(dāng)波束分布滿足(4)式的約束時,就可以采用一次一維FFT運(yùn)算優(yōu)化每一條線陣的波束形成過程,從而滿足條件1. 條件2則要求:N0=N1=…=NL-1=N,即對于所有線陣,其FFT運(yùn)算的長度均為N. 由(4)式可知,Nl的取值與cos(φ-lα)的值域集合相關(guān)。 當(dāng)l取不同值時,如果cos(φ-lα)的值域集合完全相同,則必然有Nl=N. 因此為使波束分布滿足條件2,必須對φ的選取進(jìn)行優(yōu)化。 若波束方向圖上每一個波束,其對應(yīng)的φ滿足: 此時有Nl=N,l=0,2,…,L-1,則(2)式化為 (6) p、H均為整數(shù),因此當(dāng)波束分布滿足(5)式的約束時,對于任意l,一維FFT運(yùn)算的長度相等。 除滿足(4)式和(5)式外,波束分布同樣需要滿足視場范圍及測向精度的要求。假設(shè)需要計(jì)算的波束方向圖視場角為θ∈[0,θmax],角分辨率為γ,則可以按照如下步驟,設(shè)計(jì)波束分布方式: I=sinθmaxsinγ 1)所有波束分布在I個等間距同心圓環(huán)上,即sinθ=0∶sinγ∶sinθmax,則 2)在第i個圓環(huán)上,波束為均勻分布,數(shù)量為Ji,i=0,1,2,…,I-1,i=0表示波束位于波束方向圖中心,對應(yīng)θ=0°; 3)計(jì)算θ=θmax圓環(huán)上夾角為γ的相鄰波束方位角φ的差值βγ,圖8為示意圖。 圖8 方位角差值計(jì)算示意圖Fig.8 Sketch of azimuth difference calculation 單位向量OA、OB為兩個俯仰角均為θ=θmax的波束方向向量,兩向量的夾角為角分辨率γ,向量OC、OD為OA、OB在Oxy平面內(nèi)的投影向量,則向量OC、OD的夾角即為向量OA、OB所對應(yīng)方位角的差值。 4)計(jì)算β: β=ααβγ=αkα , 當(dāng)βγ<α?xí)r,α必為β的整數(shù)倍,當(dāng)βγ≥α?xí)r,β=α,因此kα必為正整數(shù); βi,βi=2arcsin(sin(γ/2)sinθi)ββ=kiβ Ji=360βi 5)計(jì)算位于第i個圓環(huán)上相鄰波束方位角φ的差值,即每一個波束對應(yīng)的方位角φ必然為β的整數(shù)倍。該圓上包含的波束數(shù)量為,則位于第i個圓環(huán)上,第j個波束的方向矢量為u(i,j)=(sinθi·cos(jkiβ),sinθisin(jkiβ),cosθi),i=0,1,2,…,I-1,j=0,1,2,…,Ji-1. 至此,確定波束方向圖上所有需要計(jì)算的波束的方向矢量。 圖9為對應(yīng)圖7圓面陣波束方向圖的波束分布,視場范圍θ∈[0°,8°],φ∈[0°,360°],角分辨率γ=2°. 圖9 優(yōu)化的波束分布圖Fig.9 Optimized beam distribution 當(dāng)波束分布滿足(4)式和(5)式時,(6)式成立,此時波束形成過程等效為L次N點(diǎn)一維FFT運(yùn)算結(jié)果的線性疊加。 由波束分布設(shè)計(jì)過程可以看到(5)式是可以嚴(yán)格滿足的,而(4)式中的等號很難嚴(yán)格成立,但必然存在一個正整數(shù)N,使得在某一精度要求下有 (7) 則 (8) 假設(shè)波束方向圖共包含Nb個波束,則運(yùn)算量為L次N點(diǎn)FFT,(L-1)Nb次復(fù)數(shù)加法,LN次復(fù)數(shù)乘法。 N=2log2λdsinγsinβ 假設(shè)圓面陣陣元間距d=λ,期望陣元數(shù)為2 304,則根據(jù)圖5所示流程搜索到的圓面陣具有陣元T=2 314,由M=30個同心圓環(huán)陣組成。同時該圓面陣可分解為L=75條線陣,如圖10所示。 圖10 2 314陣元圓面陣陣元分布圖Fig.10 Distribution map of array elements of improved circular array 假定計(jì)算的波束方向圖視場范圍θ∈[0°,90°],φ∈[0°,360°],角分辨率γ=1°,則該波束方向圖包含Nb=14 222個波束,F(xiàn)FT長度N=8 192. 由于每條線陣原始數(shù)據(jù)長度為2M+1=61?8 192,因此可以利用Partial FFT簡化運(yùn)算,將一次8 192點(diǎn)Partial FFT分解為128次64點(diǎn)FFT. 相比于直接計(jì)算,采用頻域FFT波束形成,減少了92.5%的復(fù)數(shù)乘法以及85.6%的復(fù)數(shù)加法。 表2為圖10所示圓面陣使用(1)式直接波束形成及FFT頻域波束形成運(yùn)算量比較。 表2 運(yùn)算量比較Tab.2 Comparison of operation quantity 圖11為圖10所示圓面陣,在視場范圍θ∈[0°,90°],φ∈[0°,360°]內(nèi),對俯仰角為0°方位點(diǎn)目標(biāo)成像時的波束方向圖,主瓣寬度0.963 8°,主副瓣比19.06 dB. 圖11 對θ=0°方位點(diǎn)目標(biāo)成像時的波束方向圖Fig.11 Beam pattern of θ=0° point target imaged by improved circular array 由于(8)式中,B(k)與B(u(i,j))并非嚴(yán)格相等,因此在對數(shù)波束方向圖上,F(xiàn)FT波束形成算法計(jì)算的BP(k)與通過(1)式直接計(jì)算的BP(u(i,j))之間存在一定的誤差。該誤差與FFT長度N的取值有關(guān),N越大,誤差越小,計(jì)算量越大。在聲納設(shè)計(jì)時,需要根據(jù)實(shí)際情況取得誤差與計(jì)算量之間的折衷,以使聲納獲得最佳的綜合性能。 考察圖11中,所有波束高度高于-35 dB的波束與通過(1)式直接計(jì)算結(jié)果之間的誤差σ(i,j):σ(i,j)=|BP(u(i,j))-BP(k)|,BP(u(i,j))>-35 dB,BP(k)>-35 dB. 圖12為σ(i,j)的統(tǒng)計(jì)直方圖,平均誤差為0.016 dB,最高誤差為0.058 dB. 圖12 波束高度大于-35 dB的波束誤差統(tǒng)計(jì)Fig.12 Error statistics of beam higher than -35 dB 表3為N取不同值時,誤差與計(jì)算量的比較。 改進(jìn)型圓面陣能夠在布陣間距等于波長的條件下,對空間點(diǎn)目標(biāo)成像不出現(xiàn)假目標(biāo)[4-5],是因?yàn)榻M成圓面陣的線陣是旋轉(zhuǎn)的,而不是平行的。 表3 N取不同值時誤差與計(jì)算量的比較Tab.3 Comparison of operation quantity and errors for different N 組成圓面陣的每一條線陣的布陣間距為波長,因此對于每一條線陣而言,其對點(diǎn)目標(biāo)成像必然會出現(xiàn)柵瓣。但由于線陣是通過旋轉(zhuǎn)組成圓面陣的,因此所有線陣形成的柵瓣能量經(jīng)疊加后均勻分布在圓周上,而不是位于一點(diǎn),因此不會出現(xiàn)假目標(biāo)。 圖13為對位于θ=30°、φ=180°的點(diǎn)目標(biāo)成像的波束方向圖。 圖13 θ=30°、φ=180°方位點(diǎn)目標(biāo)成像的波束方向圖Fig.13 Beam pattern of θ=30°, φ=180° point target 圖13中點(diǎn)目標(biāo)所形成的柵瓣能量近似均勻分布在圓周上,在平面直角坐標(biāo)系下,該圓周的方程為 (x-x0)2+(y-y0)2=R2, 圖14 改進(jìn)型圓面陣與方陣波束方向圖對比Fig.14 Comparison of beam patterns of improved circular array and square array 方陣波束方向圖上,在θ=30°、φ=0°方位出現(xiàn)柵瓣,而改進(jìn)型圓面陣在該方位附近波束的最大高度為-21.9 dB. 為降低采用圓面陣的三維成像聲納的信號處理系統(tǒng)復(fù)雜度,提出改進(jìn)型圓面陣陣型設(shè)計(jì)及優(yōu)化波束方位的方法,使得改進(jìn)型圓面陣的波束形成可等效為多次一維FFT運(yùn)算結(jié)果的線性疊加。 仿真結(jié)果表明: 1)相比于傳統(tǒng)同心圓面陣的波束形成算法,改進(jìn)型圓面陣的波束形成計(jì)算量大幅度降低。 2)采用改進(jìn)型圓面陣的三維成像聲納的信號處理系統(tǒng)復(fù)雜度較低,易于實(shí)現(xiàn),使得聲納可以同時兼顧視場范圍、測向精度、運(yùn)算量、陣元數(shù)4個方面,具有良好的綜合性能。 References) [1] 陳鵬. 相控陣三維成像聲納系統(tǒng)的稀疏陣及波束形成算法研究[D]. 杭州:浙江大學(xué), 2009. CHEN Peng. Research on sparse array and beamforming algorithm for phase array three-dimension imaging sonar system[D]. Hangzhou:Zhejiang University, 2009.(in Chinese) [2] 王朋. 基于稀疏布陣的三維成像聲納信號處理算法研究[D]. 北京:中國科學(xué)院大學(xué), 2015. WANG Peng. Research on signal processing algorithm of three-dimensional acoustical imaging sonar based on sparse planar array[D]. Beijing: University of Chinese Academy of Sciences, 2015. (in Chinese) [3] 袁龍濤. 相控陣三維攝像聲納系統(tǒng)信號處理關(guān)鍵技術(shù)研究[D]. 杭州:浙江大學(xué), 2013. YUAN Long-tao. Research on key technologies of signal processing for phased array three-dimensional imaging sonar system[D]. Hangzhou:Zhejiang University, 2013.(in Chinese) [4] Tekes C, Karaman M, Degertekin F L. Optimizing circular ring arrays for forward-looking IVUS imaging[J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control, 2011, 58(12): 2596-2607. [5] Chen K S, Chen H, Wang L,et al. Modified real GA for synthesis of sparse planar circular arrays[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 274-277. [6] 楊洪亮. 基于均勻圓陣的測向算法研究[D]. 西安:西安電子科技大學(xué), 2014. YANG Hong-liang. Research on direction finding algorithm based on uniform circular array[D]. Xi’an:Xidian University, 2014.(in Chinese) [7] Palmese M,Trucco A. Three-dimensional acoustic imaging by chirp zeta transform digital beamforming[J]. IEEE Transaction on Instrumentation and Measurement, 2009, 58(7): 2080-2086. [8] 王朋, 張揚(yáng)帆, 黃勇, 等. 基于稀疏布陣的實(shí)時三維成像聲納系統(tǒng)[J]. 儀器儀表學(xué)報(bào), 2016, 37(4): 843-851. WANG Peng, ZHANG Yang-fan, HUANG Yong, et al. Real-time 3D acoustical imaging sonar system based on sparse planar array[J]. Chinese Journal of Scientific Instrument, 2016, 37(4): 843-851.(in Chinese) [9] 陳豐. Fourier變換在平面、柱、球陣波束形成和DOA估計(jì)中的應(yīng)用[D]. 杭州:浙江大學(xué), 2006. CHEN Feng. The application of Fourier transform to planar,cylindrical and spherical array beamforming and DOA estimation[D]. Hangzhou:Zhejiang University, 2006.(in Chinese) [10] 印明明, 劉平香. GPU實(shí)現(xiàn)水下三維成像研究[J]. 聲學(xué)技術(shù), 2014, 33(5): 53-57. YIN Ming-ming, LIU Ping-xiang. Study on 3D image sonar based on GPU[J]. Technical Acoustics, 2014, 33(5): 53-57.(in Chinese) [11] 胡將. 基于Kintex-7的三維聲學(xué)成像主信號處理系統(tǒng)硬件設(shè)計(jì)[D]. 杭州:浙江大學(xué), 2016: 17-47. HU Jiang. Hardware design of three-dimensional acoustic imaging main signal processing system based on Kintex-7 [D]. Hangzhou:Zhejiang University, 2016: 17-47.(in Chinese) [12] 張沛霖, 張仲淵. 壓電測量[M]. 北京: 國防工業(yè)出版社, 1983: 63-67. ZHANG Pei-lin, ZHANG Zhong-yuan. Piezoelectric measurement[M]. Beijing:National Defense Industry Press, 1983: 63-67.(in Chinese) [13] 蔣毅. 天線陣列陣元位置優(yōu)化方法研究[D]. 哈爾濱:哈爾濱工程大學(xué), 2013. JIANG Yi. Research on the optimum method for element position of antenna arrays[D]. Harbin: Harbin Engineering University, 2013.(in Chinese) [14] Cooklev T. Generalized and partial FFT[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 1995(9):1466-1473. Design of Fast Beam Forming of Improved Circular Planar Array YU Di-fei, ZHANG Chun-hua, HUANG Yong (University of Chinese Academy of Sciences, Beijing 100190, China) In order to reduce the computational complexity of beam forming of 3D imaging sonar based on circular planar array, a method of improving the array design and optimizing the beam azimuth is proposed. The improved circular array consists of a plurality of linear arrays passing through the center, and the beam forming is equivalent to the superposition of the beam forming of all the linear arrays. By optimizing the beam azimuth, the beam forming process of each linear array is equivalent to a one-dimensional fast Fourier transform operation of equal length. The simulated results show that the beam forming computation of the improved circular array is significantly lower than that of the direct calculation. The use of improved circular array can significantly reduce the complexity of the signal processing system and improve the comprehensive performance of 3D imaging sonar. acoustics; 3D underwater sonar; circular arrays; beam pattern; fast Fourier transform 2016-08-11 國家自然科學(xué)基金項(xiàng)目(11304343) 于滌非(1982—), 男, 博士研究生。 E-mail: nacassoce@163.com 張春華(1962—), 男, 研究員, 博士生導(dǎo)師。 E-mail: zch@mail.ioa.ac.cn TB565+.2; TN911.72 A 1000-1093(2017)05-0959-09 10.3969/j.issn.1000-1093.2017.05.016
3 波束方向圖波束分布設(shè)計(jì)
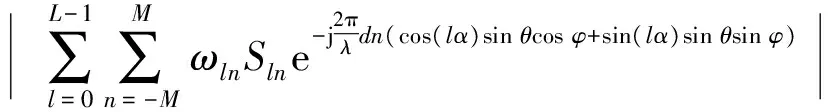





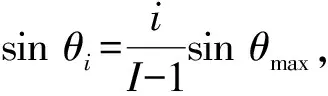
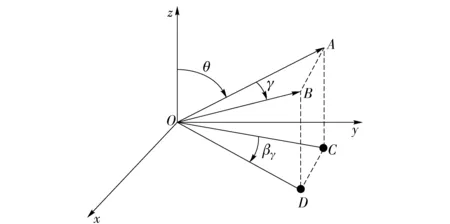

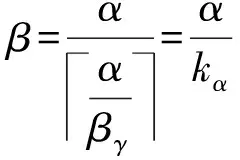


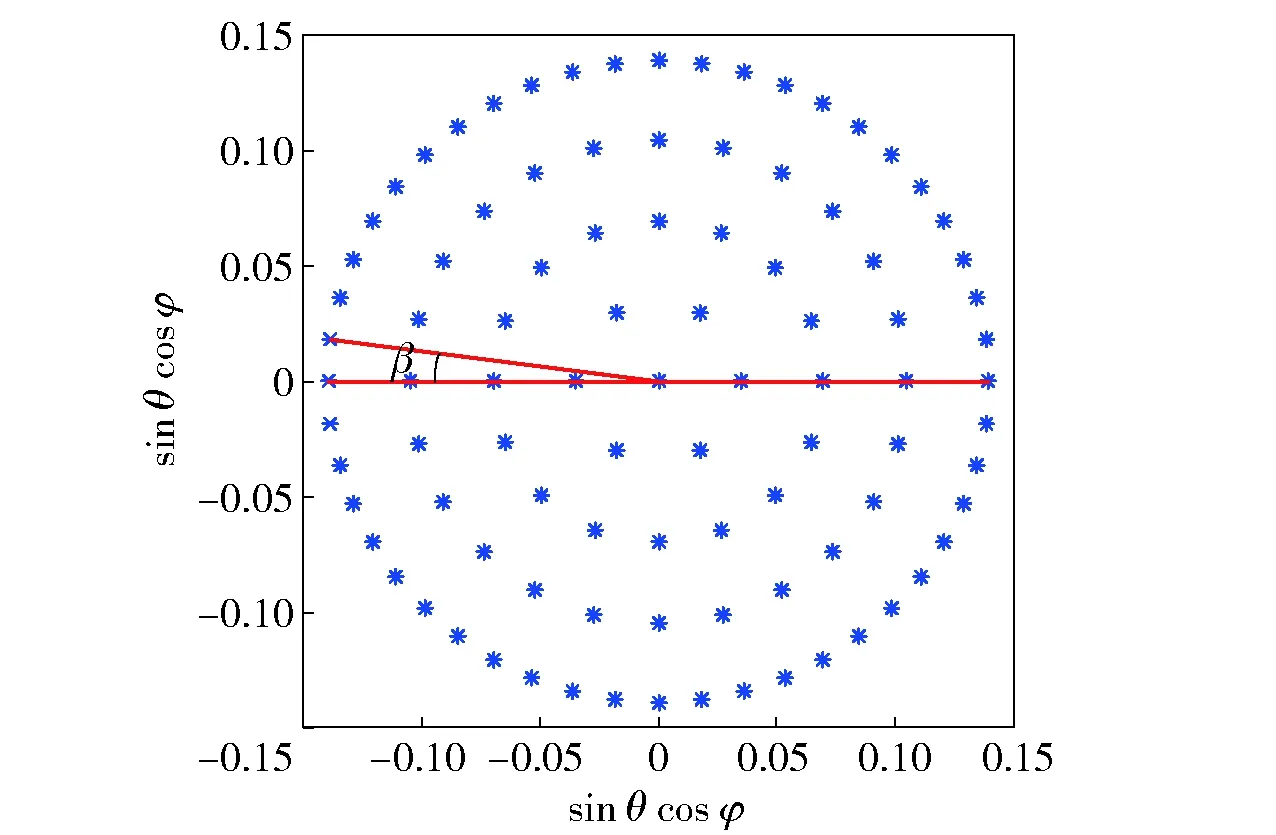
4 圓面陣遠(yuǎn)場頻域FFT波束形成
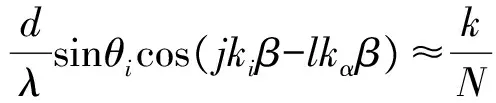
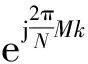







5 改進(jìn)型圓面陣柵瓣分析


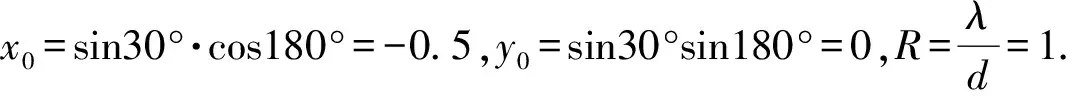
6 結(jié)論

