攝動落點預測法的快速建模與基于精度最優的分段預測控制法

王鈺， 于紀言， 王曉鳴

(南京理工大學 智能彈藥技術國防重點學科實驗室， 江蘇 南京 210094)

?

攝動落點預測法的快速建模與基于精度最優的分段預測控制法

王鈺， 于紀言， 王曉鳴

(南京理工大學 智能彈藥技術國防重點學科實驗室， 江蘇 南京 210094)

快速的高精度落點預測是實現高旋彈丸彈道預測修正或制導的關鍵，基于基準彈道的攝動(PP)預測法能夠較好地平衡計算精度與效率。為解決PP預測法難以快速適應環境與目標的問題，結合攝動理論與分步逼近法實現初始發射條件及基準彈道的快速確定，并根據理論簡化推導出攝動模型參數計算方法。通過彈道仿真與無控試驗驗證其可行性，結果表明:該方法可快速完成發射參量計算與攝動預測建模；與修正質點彈道(MPT)預測法相比，彈道前段PP預測法預測精度較優，彈道后段略差。綜合PP預測法與MPT預測法計算速度與精度特點，提出結合PP與MPT的分段預測法，經蒙特卡洛仿真，分段預測法的修正效果相較于單一的PP或MPT預測法更優。

兵器科學與技術； 制導炮彈； 快速落點預測建模； 攝動理論； 基準彈道生成； 分段預測法

0 引言

制導/修正彈藥的制導方案主要包括彈道成型、彈道預測和彈道追蹤法[1]。對于控制效能較小的彈丸(如雙旋式彈道修正彈)，彈道預測法較為適用。彈道預測法的關鍵在于快速的、高精度的彈道落點預測。落點預測方法主要包括線性擬合和彈道積分外推方法。線性擬合方法計算速度快，輸入參量少，但計算精度較差。為提高預測精度，Ghosh等[2]和曹營軍等[3]提出了基于神經網絡的離線線性擬合方法，固定條件下其預測精度較高，但使用范圍受限。Kramer等[4]提出在線訓練模型方案，但不適用于有控的情況。積分外推法計算精度高，但占用計算資源多、計算時間長。為簡化計算，Costello等[5]、Hain等[6-7]、李興隆等[8]提出并改進了修正線性彈道理論，將其分別運用于平射彈道、高旋曲射彈道、末段修正彈道，研究顯示相較于傳統的積分外推法其計算速度更快，但需全彈道狀態可測，實際運用受限。為平衡在線計算速度與計算精度，李超旺等[9]、王毅等[10]和田在克等[11]提出了基于基準彈道的攝動(PP)預測法，并將其分別運用于火箭彈和修正榴彈，均獲得較好的預測精度與修正效果。該方法使用彈道積分法求解基準彈道與攝動模型參數，根據攝動多項式模型進行在線落點預測。現有的PP理論預測方法中模型參數均通過彈道仿真求解，特定目標、環境下的攝動模型參數求解需較長時間，難以滿足快速裝定要求，且對于固定目標基準彈道的確定方法均沒有仔細研究。為解決PP預測方法的環境- 目標適應性問題，本文基于攝動理論提出一種針對固定目標點的發射參數與基準彈道快速生成方法，并根據理論簡化推導出攝動模型參數快速解算方法。

1 發射參數優化及基準彈道生成

由于基準彈道是PP預測法的基準，其計算誤差將直接影響預測精度；由攝動理論原理可知，實際彈道與基準彈道偏差越大，預測誤差越大；對于修正能力較弱的彈丸，為提高命中率，應保證無控彈丸落點盡量接近目標點。故根據射擊前實測氣象條件、目標位置等快速計算無控落點與目標點接近的發射參數與基準彈道是提高PP預測法預測精度與命中率的關鍵。

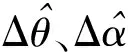
圖1 基準彈道生成流程Fig.1 Flowchart of base trajectory generation

已知發射點O與目標點的GPS坐標，為方便計算與控制，根據(1)式將目標點GPS坐標轉換至以發射點為原點，射向方向為x軸的射向坐標系。坐標轉換角度關系如圖2所示。

圖2 坐標轉換示意圖Fig.2 Schematic diagram of coordinate transformation

(1)

式中：[xT,zT]=IT；D表示發射點到目標點在地球表面的最短距離；α表示目標點與發射點連線與真北方向的夾角，向東為正；γ為坐標北方向與真北方向間的夾角。α、D、γ只與發射點和目標點的坐標相關，與射向角無關，其計算公式可參考文獻[12]。

由于彈丸初速非連續可調，為提高能量利用效率，將發射點與目標點距離與可選擇的各彈丸初速對應的最大射程相比較，選取最大射程稍大于發射點與目標距離的彈丸初速值v0，在該初速下根據經驗選取參考射角與射向角。根據設定的初始參量，代入發射前實測的氣象數據，計算得參考彈道落點Iref=(xref,zref). 當參考落點與目標點偏差較大時，需調整發射參量(射角和射向角)使其接近目標點，從而減小修正距離。參考落點與目標點的距離記為(xT-xref,zT-zref)=(ΔxT,ΔzT). 不考慮發射與飛行過程中的干擾及參數誤差，彈丸無控落點可表示為射角與射向角的函數：

IB=[x,z]=f(θ,αN).

(2)

由攝動理論，落點位置可根據(3)式近似計算，其中偏導數可使用仿真方法依據偏導數定義(見參考文獻[13])近似求解。

(3)

(4)

(5)

2 PP落點預測方法

為適應高旋炮彈飛行時間短、修正能力較弱的特點，修正/制導炮彈對在線計算速度、控制方法的能效要求較高。相較于彈道成型、彈道追蹤方法，落點預測控制法的控制能效最高[1]。為更好地平衡落點預測精度與計算速度，本文主要研究基于PP落點預測法。為提高任意環境、目標下攝動建模速度以滿足快速裝定要求，根據理論簡化推導，提出了模型參數快速計算方法。

2.1 攝動預測模型

IA=[xIA,zIA]=f(P,v,a).

(6)

由其物理性質可知，(6)式是連續函數，故落點表達式可用泰勒級數公式近似為

(7)

式中：R=[r1…rn]為落點方程的自變向量，[r1…rn]=[xyzvxvyvzaxayaz]；下標B表示基準彈道相關量；下標A表示實際彈道相關量；o(RA-RB)表示與自變量相關的高階函數。由泰勒公式的性質，在RB的鄰域范圍內，落點的泰勒級數公式收斂，故當實際彈道與基準彈道較為接近時，落點位置可由(7)式近似計算。

2.2 模型參數求解

PP預測法預測落點的關鍵在于偏導參數計算。為滿足發射前快速裝定的要求，本文根據偏導數的定義，經理論推導求得偏導參數的迭代計算公式。

2.2.1 1階位置偏導數

根據偏導數定義，某彈道點對應的?IA/?ri為

(8)

(9)

式中：vxe、vye、vze分別表示落地時彈丸速度在慣性基準系x、y、z軸的投影。

2.2.2 1階速度偏導數

假設實際彈道vi(i為x、y或z)與基準彈道僅相差Δvi，由于氣動力與彈丸飛行速度相關，后續飛行彈道中彈丸所受氣動力(矩)與基準彈道均不相同，故需迭代求解。速度偏導數計算流程圖如圖3所示。

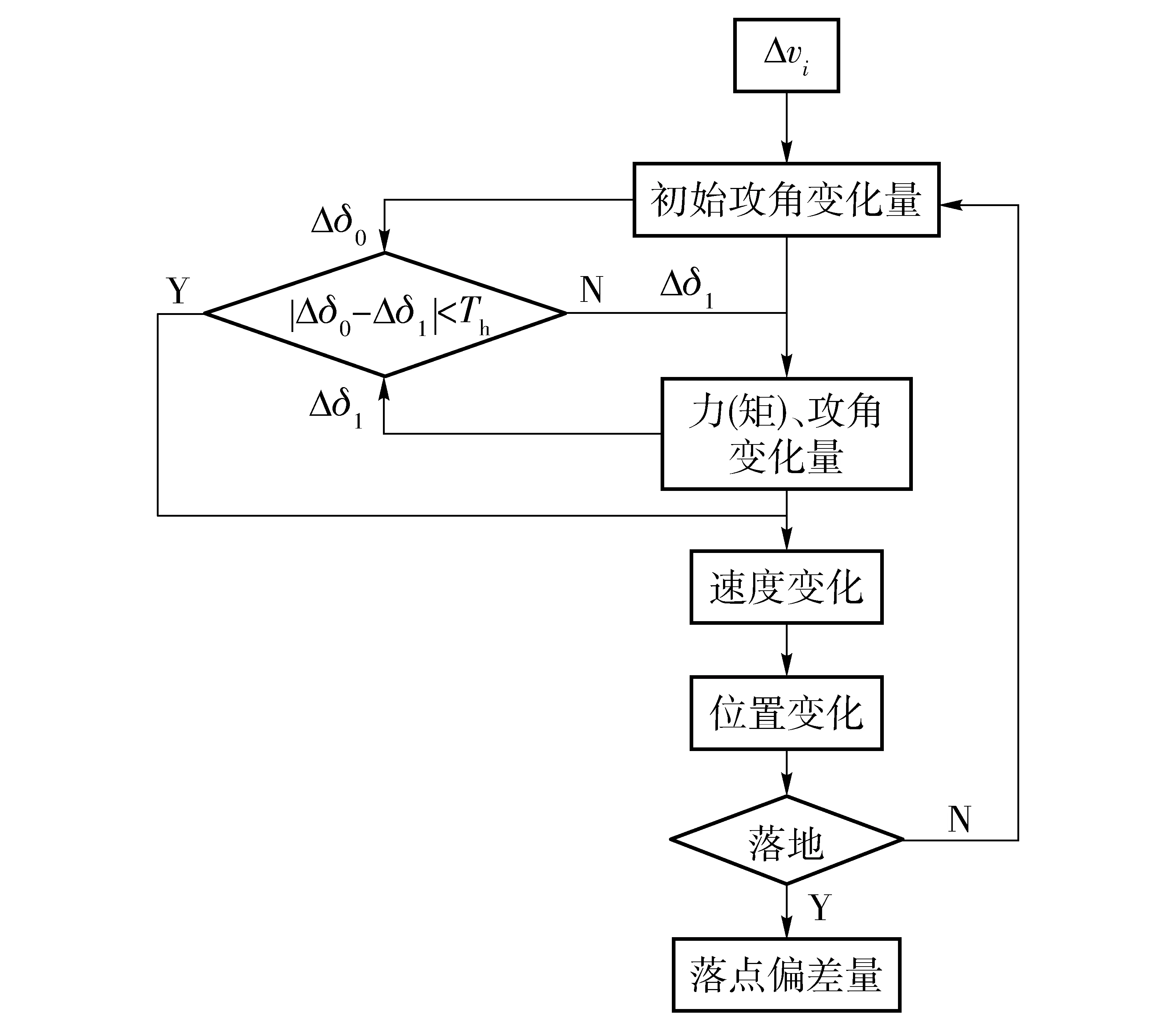
圖3 速度偏導數計算流程圖Fig.3 Calculational flowchart of partial derivation of velocity

力矩變化引起彈丸飛行姿態變化，而姿態變化又對氣動力(矩)產生影響，所以需迭代求解彈丸姿態角。為簡化求解，本文選用動力平衡角的變化量近似代替攻角變化量。動力平衡角的矢量定義為

αR=i×(ε×i)=ε-cosδi，

(10)

式中：i、ε分別表示速度與彈軸的單位矢量；δ表示彈丸總攻角。

根據參考文獻[14]中動力平衡角的近似解：αR≈2(ρSdv4CMα)-1Ixpg×v，可得動力平衡角變化量計算公式：

(11)

式中：vA和vB分別表示實際彈道與基準彈道中的相對速度，vA和vB為其矢量形式；Ix表示彈丸對x軸的慣性矩；S為彈丸迎風面積；d表示彈丸直徑；ρ表示空氣密度；p表示彈丸滾轉角速率；g表示重力加速度；CAMα和CBMα分別表示實際彈道與基準彈道的翻轉力矩系數，可用CMα0+CMα2δ2近似計算，CMα0、CMα2分別為翻轉力矩對攻角的1階和3階導數。

由氣動力定義可得實際彈道與基準彈道所受外力之差為

(12)

式中：Δ(f)=fA-fB，即實際彈道與基準彈道對應的f值之差；CLα為升力系數；CD為阻力系數；Cnpα為馬格努斯力系數導數。將(12)式代入(10)式可得與速度、動力平衡角相關的ΔF表達式：

(13)

t0時刻Δvi初始偏差對應的落點變化量ΔI可根據(14)式迭代計算：

(14)

當Δvi較小時，落點變化量相對于速度的偏導數可由(15)式近似求解：

(15)

2.2.3 1階加速度偏導數

由于隨機風、氣動參數誤差、控制器作用等因素，彈丸實際受力與仿真結果不完全一致，即當基準彈道與實際彈道的位置、速度一致時，由于干擾作用加速度也可能存在區別。彈道預測的目的是計算某飛行狀態下彈丸無控飛行落點位置，故預測段無控制力作用。因為實測加速度偏差值包含控制力相關項與位置、速度偏差相關項，所以實際加速度偏差Δa=Δam-Δac-ΔavP，其中Δa為(7)式中的自變量偏差的加速度相關項，Δam表示實測彈丸加速度與基準彈道對應加速度之差，Δac表示控制力對應的彈丸加速度，ΔavP表示速度、位置差引起的加速度差。

由于加速度偏差由擾動引起，而干擾作用時間、變化狀態未知，故無法準確計算擾動加速度引起的落點偏差；Δac和ΔavP均由計算獲得，存在計算誤差；對于單衛星測量系統，加速度無法直接測量，Δam存在間接測量誤差。相對而言，干擾加速度通常為小量，故忽略(7)式中加速度項。

2.2.4 高階偏導數

由定義可知n階偏導數可根據公式(16)計算：

(16)

式中：ri+1，…，ri+n表示I表達式中的任意n個自變量，可重復。將1階偏導代入(16)式即可求解任意階偏導數。

3 PP預測法仿真分析

為驗證上述理論的可行性，對155 mm彈丸進行仿真，彈丸參數如表1所示，其中lCG表示舵翼控制力作用點與全彈質心的軸向距離。仿真主要包括：

表1 155 mm彈丸參數表Tab.1 Parameters of 155 mm caliber projectile

1)基準彈道生成(基于2.1節方法)；

2)不同階數攝動模型對比；

3)攝動理論模型建立速度(基于2.2節方法)，及其在仿真與無控試驗下的落點預測精度。

3.1 基準彈道生成

為評估基準彈道生成方法的可行性、精度及計算速度，假設發射點GPS坐標為[東經105°，北緯38°]；目標點坐標為[東經104°50′，北緯38°10′]. 選取初始射向角：北偏西41°，由(1)式求得發射系下目標位置：[23 570 m，1 171 m]. 由目標點與發射點的距離選擇彈丸初速805 m/s(最大射程約25 km)，初始射角45°. 氣象條件為無控飛行試驗實測的氣象數據。落點與目標點距離閾值設置為30 m.

為選取合適的分步優化自變量區間，在參考點θref=40°、αNref=-40.4°處建立模型(見(3)式)，根據模型求解不同Δθ、ΔαN對應的射程、橫偏預測值，并與相同條件下的仿真落點比較。不同Δθ、ΔαN對應的射程、橫偏預測誤差分別如圖4和圖5所示。

圖4 Δθ、ΔαN射程預測誤差圖Fig.4 Δθ,ΔαN versus prediction error of range

圖5 Δθ、ΔαN橫偏預測誤差圖Fig.5 Δθ,ΔαN versus prediction error of deflection

由圖4和圖5可知：|Δθ|和|ΔαN|越大，PP預測法預測誤差越大；射角偏差對預測的影響大于射向角偏差；射向角偏差對射程預測的影響大于橫偏；當|Δθ|<5°且|ΔαN|<5°時，PP預測法預測總誤差小于250 m. 綜合考慮預測誤差和迭代次數，[ΔθD,ΔθU]、[ΔαND,ΔαNU]均設定為[-5°,5°]。迭代逼近過程中，每步計算結果如表2所示。發射參量優化使用計算機(相關配置參數如表3所示)通過Matlab軟件計算，使用軟件自帶計時器測得優化計算總耗時619.8 s.

表2 發射參量分步計算結果Tab.2 Calculated results of launching parameters

表3 計算機配置參數Tab.3 Computer configuration data

3.2 模型階數選擇

為研究攝動模型的階數對落點預測精度的影響，從而選擇合適的模型階數，分別使用1階、2階、3階模型對彈道落點進行預測，其落點預測誤差如圖6所示；不同階數模型參數求解與預測所用時間(計算設備如表3所示)如表4所示。

圖6 不同階數模型的PP預測法預測誤差Fig.6 Predicted errors of perturbation methods with different model orders表4 不同階數模型建模與預測時間Tab.4 Modeling and predicting time of different model orders

模型階數建模時間/s預測時間/ms11326304249657023124101325

由圖6可知，1階、2階、3階模型的彈道預測誤差均較為接近，1階模型預測精度略遜于2階、3階模型，而2階與3階模型的預測結果幾乎一致。由表 4可知，階數越高，建模與預測時間越長；1階與2階建模時間均小于1 min，預測時間均小于10 ms；3階建模時間大于2階的2倍。綜上所述，2階攝動模型能更好地滿足計算精度與速度的需求。

3.3 模型參數求解

為驗證2.2節攝動模型參數求解方法的可行性，通過Matlab編程(計算設備配置見表3)，分別使用仿真解法(見參考文獻[9-11])與簡化解法(見2.2節)求解相同基準彈道、相同彈丸與環境參數情況下的2階攝動模型參數，并比較兩種方法的計算時間與預測精度。

由于不同彈道時刻對應的攝動模型參數變化較大，按飛行時間每隔5 s計算一組攝動參數，落點預測時根據時間插值求解。不同的參數計算方法對應的2階攝動模型參數計算時間如表5所示，由表可知，簡化計算方法的計算時間遠小于仿真方法。

表5 不同方法模型參數計算時間Tab.5 Parameters computing time of different methods

為研究簡化計算方法對彈丸落點預測精度的影響，比較相同情況下，不同方法建立的攝動模型對應的全彈道PP預測誤差，如圖7所示，其中飛行前10 s用于測量、控制系統初始化，故預測從10 s開始。由圖7可知飛行10 s之后，簡化算法與仿真方法計算的攝動模型預測誤差均40 m以內；35 s之前簡化算法誤差略大；35 s之后兩種算法對應的預測精度近似。綜上所述，簡化的參數計算方法可在保證一定精度的前提下大幅提高建模效率。

圖7 不同參數算法的PP預測誤差Fig.7 Predicted errors of different calculation methods

3.4 無控彈道預測精度

為分析PP預測法(簡化計算參數)的預測精度，分別以仿真無控彈道與無控實測彈道為實際彈道，對彈道落點進行預測并與實際落點和修正質點彈道積分外推(MPT)預測法預測結果比較。

3.4.1 仿真彈道預測

為分析PP預測法預測精度，通過仿真向實際彈道添加發射、氣象、測量等干擾，其中包括發射高低角、方向角、初速、風速偏差、彈丸氣動參數與GPS測量誤差，各項干擾均為零均值正態分布，其標準差如表6所示。200組該隨機干擾下無控彈道的全彈道2階PP預測法預測值，每組彈道對應的實際與基準彈道落點距離、10 s和40 s后最大預測誤差如圖8所示，為方便觀察分析，200組數據按實際與基準彈道落點距離遞增順序排列。

表6 發射、飛行與測量干擾參量表Tab.6 Launching, flight and measurementinterference parameters

圖8 不同無控仿真彈道預測誤差Fig.8 Prediced errors of different uncontrolled trajectories

由圖 8可知：

1)實際落點到目標點距離最大為555 m，10 s后的最大預測誤差為128 m，40 s后最大預測誤差為43 m;

2)每組彈道40 s后最大預測誤差均小于10 s后的最大誤差，則預測誤差隨時間推移逐漸減小；

3)隨實際彈道與基準彈道落點距離增大，40 s與10 s后的最大預測誤差均沒有明顯變大趨勢，可見預測誤差與實際彈道—基準彈道落點距離無明顯關系。

保持實際彈道其余發射與飛行參量不變，分別改變實際彈道與基準彈道初始速度、射向角、射角之差，預測誤差分別如圖 9、圖 10和圖 11所示。

圖9 不同初速差下無控彈道預測誤差Fig.9 Predicted errors of uncontrolled trajectories with different launch velocities

圖10 不同射向角下無控彈道預測誤差Fig.10 Prediction errors of uncontrolled trajectories with different gun azimuths

圖11 不同射角下無控彈道預測誤差Fig.11 Predicted errors of uncontrolled trajectories with different gun elevations

由圖9～圖11可見：當其余彈道干擾相同時，實際彈道與基準彈道的初速差或射角差越大時，預測誤差越大；射向角偏差對落點距離預測誤差影響不大。

3.4.2 無控試驗彈道預測

為驗證實際飛行情況下PP預測法的預測精度，對實際無控飛行雷達數據進行全彈道落點預測，并與MPT預測法預測結果對比。其中PP預測法的基準彈道(落點與實際無控落點偏差約200 m)及其對應的偏導數根據理想發射條件計算獲得；兩種模型計算的氣象條件均使用發射前測量數據，氣動參數由氣動仿真結合風洞試驗獲得。兩種模型的全彈道預測誤差如圖12所示。由圖12可知：

1)相對于MPT預測法，PP預測法預測對彈道各參數的測量誤差等干擾更敏感，故PP預測法落點預測值在全彈道范圍內波動更明顯;

2)由于彈道起始段MPT預測法對橫偏預測誤差較大，故在彈道前段其預測精度不及PP預測法；但PP預測法受干擾等情況影響明顯，彈道末段預測精度略差。

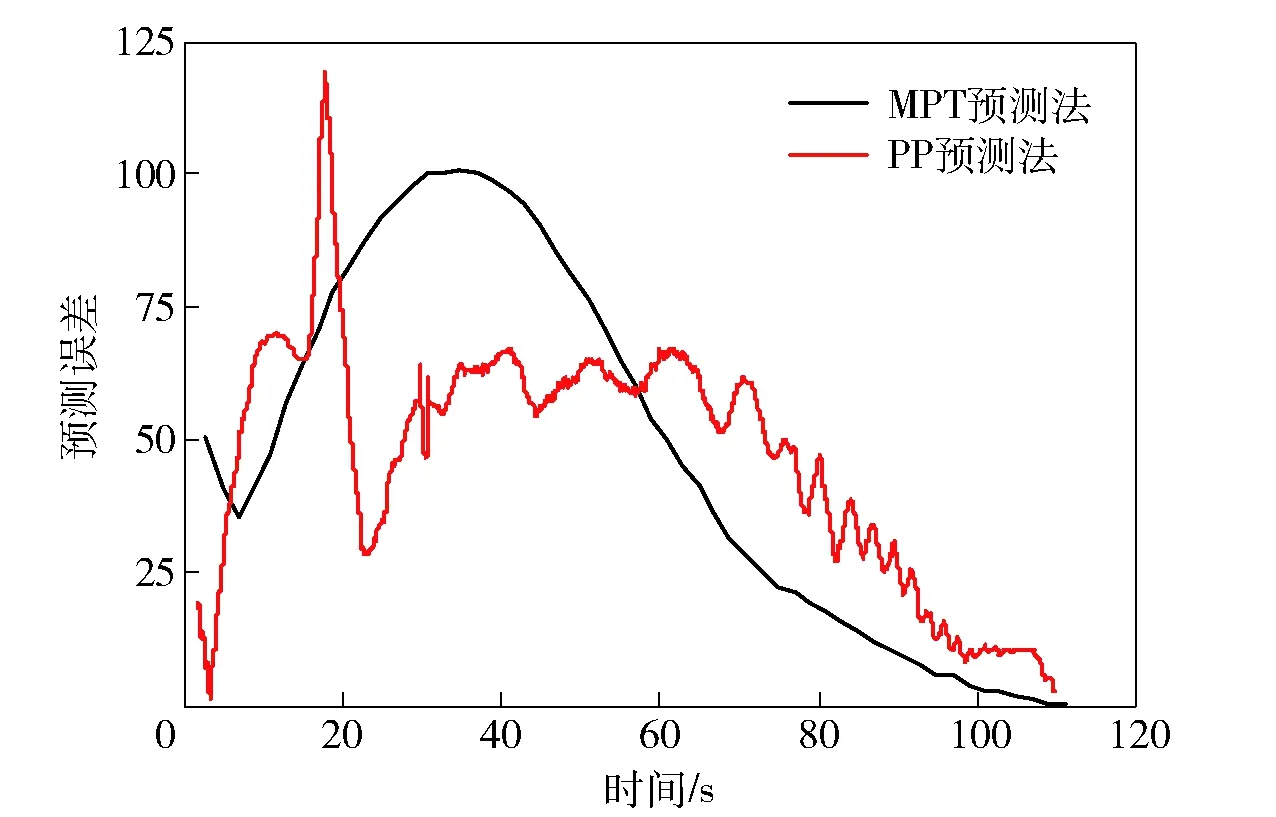
圖12 無控試驗彈道預測誤差Fig.12 Predicted errors of uncontrolled experiment

為比較PP預測法與MPT預測法的計算時間，使用相同的計算設備(配置見表3)、相同的計算軟件(Matlab)，統計不同算法對應的落點預測時間如表 7所示。不同起始預測時刻對應的MPT預測法計算時間不同(表中起始計算時刻為發射時刻至落地前3 s)，而PP預測法預測時間與起始預測時刻無關。由表7可知，全彈道范圍內，PP預測法預測時間均遠小于MPT預測法。

表7 不同方法下落點預測時間Tab.7 Computing time of different prediction methods

4 分段預測法

根據3.4節可知，彈道前段PP預測法預測精度優于MPT預測法，后段相反；且后段MPT預測法預測時間較前段明顯縮短，經程序優化可適應在線計算要求。綜上所述，為綜合PP預測法與MPT預測法的優勢，提出分段(PW)預測法，即彈道前段采用PP預測法，后段采用MPT預測法進行落點預測控制。控制指令計算公式為

(17)

(18)

式中：γc表示舵指令；φF表示提前相位角(計算方法參考文獻[15])；ΔI為預測落點與目標點的位置差；I(*)表示使用*法預測的落點位置；ts為分段時刻，根據仿真求解全彈道預測精度最優化求解：

(19)

te表示飛行總時長，ΔIr為真實落點與目標點的位置差。

4.1 預測精度比較

為驗證PW預測方法的預測精度，分別使用2階PP預測法、MPT預測法以及PW預測法對相同情況下的無控彈道進行全彈道落點預測，實際彈道干擾如表6所示，預測結果如圖13所示，其中ts根據(19)式選為60 s. 由圖13可知，PW預測法的預測精度在全彈道范圍內均優于單一的PP預測法與MPT預測法。

圖13 不同預測方法對應的無控仿真彈道預測誤差Fig.13 Predicted errors of uncontrolled trajectory simulation of different methods

4.2 控制效果比較

為比較不同控制方法對彈丸落點的控制效果，使用蒙特卡洛法(500個樣本點)分別計算相同彈道干擾條件下(如表6所示)，無控與不同預測模型(2階PP、MPT、PW)對應的有控落點分布情況。3種預測控制方法起控時間均為40 s，控制指令更新周期均為0.1 s，φF為155°，ts為60 s. 無控、PP預測法、MPT預測法與PW預測法預測控制的落點散布分別如圖14～圖17所示；對應的圓概率誤差(CEP)、落點- 目標平均距離如表8所示。

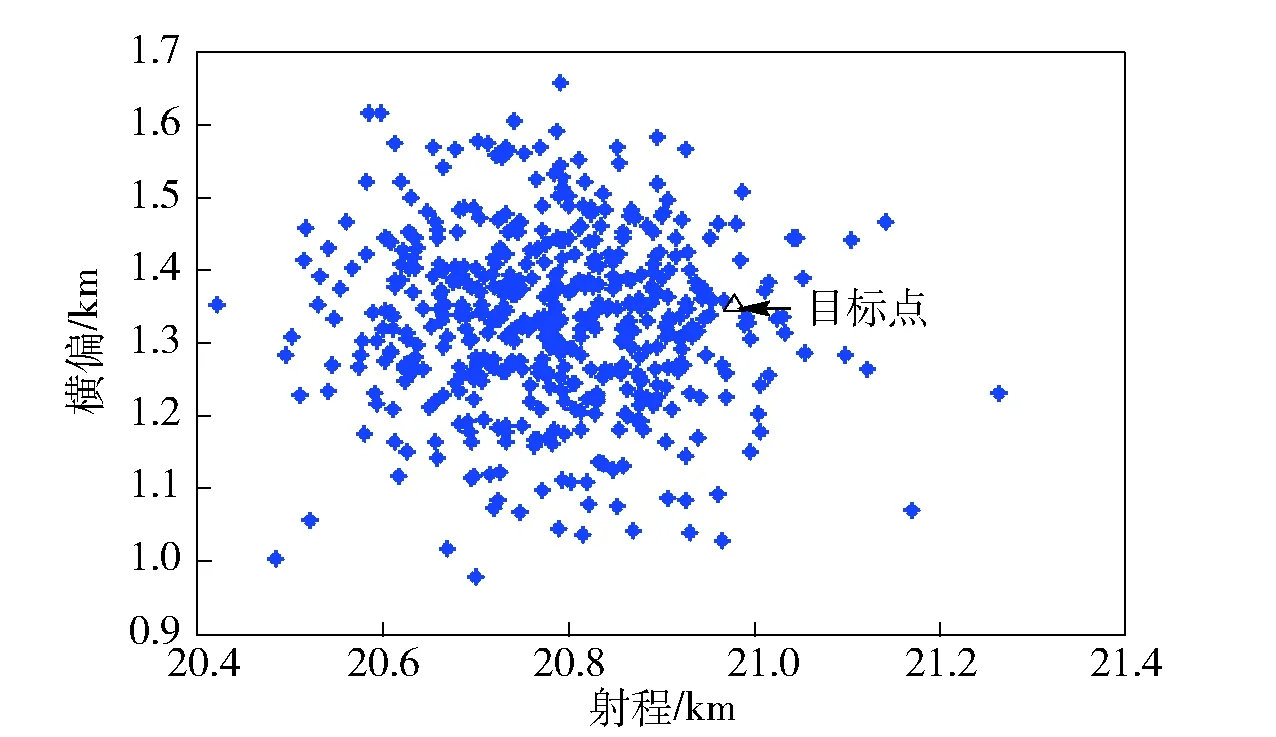
圖14 無控落點散布圖Fig.14 Impact dispersion of uncontrolled projectiles

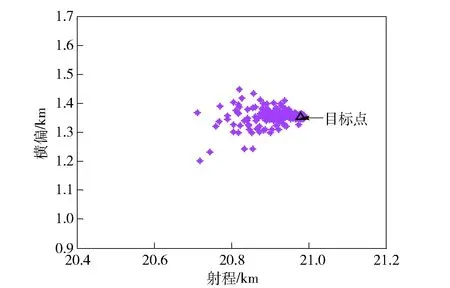
圖15 2階PP預測法預測控制落點散布圖Fig.15 Impact dispersion of projectiles controlled by PP method

由圖14～圖17與表8可知，PP預測法、MPT預測法與PW預測法均能有效減小彈丸散布，并使彈丸靠近目標點；落點CEP值MPT預測法>PP預測法>PW預測法；落點- 目標平均距離MPT預測法>PP預測法>PW預測法。綜上所述，PP預測法修正效果優于MPT預測法；而PW預測法略優于PP預測法。但由于修正能力(40 s起控該彈丸修正能力約為300 m)不足，3種預測方法均難以將偏差較大的落點修正至目標點附近；可考慮通過增大控制力或提前修正的方式增大彈丸控制能力，以改善修正效果。

圖16 MPT預測法預測控制落點散布圖Fig.16 Impact dispersion of projectiles controlled by MPT method

圖17 PW預測法預測控制落點散布圖Fig.17 Impact dispersion of projectiles controlled by PW method表8 不同情況下落點統計量Tab.8 Statistics of impact-points in different conditions

方法CEP/mΔX/mΔZ/m無控14216-19649-2114PP預測法3917-2466037MPT預測法4918-38642041PW預測法3534-2224521

5 結論

本文建立了基于攝動理論、逐次逼近優化求解方法的基準彈道與發射條件快速求解方法；并根據理論近似推導，提出了攝動模型偏導數的快速計算方法。該方法能有效縮短在線彈道預測與發射前準備時間，為PP落點預測方法的實際運用提供基礎。通過仿真分析攝動預測精度與速度特點，并與MPT預測法比較，從而提出綜合PP預測法與MPT預測法的PW預測方法。

經彈道仿真與無控飛行試驗驗證可知：

1)基于攝動理論的基準彈道求解方法可在620 s內生成落點與目標點距離小于30 m的基準彈道。

2)綜合考慮計算時間與計算精度，2階攝動測模型較優。

3)根據理論簡化推導的PP預測快速建模方法，可在50 s內完成已知基準彈道與環境參數下的2階攝動模型建模，計算時間遠小于仿真計算方法。

4)表6對應的干擾條件下，簡化方法建立的攝動模型，預測誤差有明顯收斂性，且40 s之后預測誤差均小于50 m；相比于MPT預測法，PP預測法計算時間明顯縮短，彈道前段預測精度更優，后段略差。

5)蒙特卡洛仿真分析可知相較于單一的PP預測法或MPT預測法，PW預測法的控制效果更優。

References)

[1] John W C, Robinson. On guidance and control for guided artillery projectiles, Part 1: general considerations, FOI-R-3291-SE[R]. Sweden: Swedish Defence Research Agency， 2011.

[2] Ghosh A K, Prakash O. Neural models for predicting trajectory performance of an artillery rocket[J]. Journal of Aerospace Computing, Information and Communication, 2004, 1(2): 112-115.

[3] 曹營軍, 朱宗平,李麗春, 等. 基于BP人工神經網絡的末修彈落點預測導引模式[J]. 彈箭與制導學報, 2011, 31(6): 76-78. CAO Ying-jun, ZHU Zong-ping. LI Li-chun, et al. Impact point prediction guidance mode of terminal trajectory correction projectile based on BP artificial neural networks[J]. Journal of Projectile, Rockets, Missile and Guidance, 2011, 31(6):76-78. (in Chinese)

[4] Kramer K A, Stubberud S C. Impact time and point predicted using a neural extended Kalman filter[C]∥The 2nd International

Conference on Intelligent Sensors, Sensor Networks and Information Processing. Melbourne, Australia: IEEE, 2005.

[5] Costello M, Peterson A. Linear theoty of a dual-spin projectile in atmospheric flight[J]. Journal of Guidance, Control and Dynamics, 2000, 23(5):789-797.

[6] Hainz L C, Costello M. Modified projectile linear theory for rapid trajectory prediction[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(5): 1006-1014.

[7] Hainz L C, Costello M. In flight projecitle impact point prediction[C]∥Atmospheric Flight Mechanics Conference and Exhibit. Providence, RI, US: AIAA, 2004.

[8] 李興隆, 賈方秀, 王曉鳴, 等, 基于線性彈道模型的末段修正彈落點預測[J]. 兵工學報, 2015, 36(7):1188-1194. LI Xing-long, JIA Fang-xiu, WANG Xiao-ming. Impact point prediction of terminal correction projectile based on linear trajectory model[J]. Acta Armamentarii, 2015, 36(7):1188-1194. (in Chinese)

[9] 李超旺, 高敏, 宋衛東. 基于攝動原理的火箭彈落點實時預測[J]. 兵工學報, 2014, 35(8):1164-1171. LI Chao-wang, GAO Min, SONG Wei-dong. Real-time impact point prediction of rocket projectile based on perturbation theory[J]. Acta Armamentarii, 2014, 35(8): 1164-1171.(in Chinese)

[10] 王毅, 宋衛東, 宋謝恩, 等. 基于攝動理論的彈道修正榴彈落點偏差預測[J]. 彈道學報, 2015, 27(3): 18-23. WANG Yi, SONG Wei-dong, Song Xie-en. Impact-point prediction of trajectory-correction grenade based on perturbation theory[J]. Journal of Ballistics, 2015,27(3): 18-23. (in Chinese)

[11] 田在克, 楊鎖昌, 馮德龍, 等. 基于攝動理論的落點預測算法研究 [J]. 現代防御技術, 2014, 42(3):86-90. TIAN Zai-ke, YANG Suo-chang, FENG De-long, et al. Impact point prediction algorithm based on perturbation theory[J]. Modern Defence Technology, 2014, 42(3):86-90. (in Chinese)

[12] 邱冬煒. GPS坐標轉換系統模型的研究[D]. 北京: 北京交通大學, 2005:22-27. QIU Dong-wei. Research of GPS coordinate system transformation model[D]. Beijing: Beijing Jiaotong University, 2005: 22-27. (in Chinese)

[13] 南京理工大學應用數學系. 高等數學：下冊[M]. 北京：高等教育出版社, 2008: 72. Department of Applied Mathematics, Nanjing University of Science and Technology. Higher mathematics: volume 2 [M]. Beijing: Higher Education Press, 2008:72. (in Chinese)

[14] McCoy R L. Modern exterior ballistics[M]. Atglen，PA, US:Shiffer Publishing Ltd, 1999:214.

[15] 王鈺,王曉鳴,程杰, 等. 基于等效力方法的雙旋彈側向控制力落點響應分析[J]. 兵工學報, 2016, 37(8):1379-1387. WANG Yu, WANG Xiao-ming, CHENG Jie, et al. Analysis on impact ponint response of a dual-spin projectile with lateral force based on equivalent force method[J]. Acta Armamentarii, 2016, 37(8):1379-1387. (in Chinese)

Rapid Impact-point Prediction Modeling Based on Perturbation Theory andPiecewise Prediction Control Method

WANG Yu, YU Ji-yan, WANG Xiao-ming

(Ministerial Key Laboratory of ZNDY, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China)

The rapid and accurate impact-point prediction is a key to correct or guide a high-spinning projectile， and the impact-point prediction based on perturbation(PP) with base trajectory can balance the calculation efficiency and precision. As the parameters of the perturbation model cannot be calculated rapidly with the variation in environment and target, a method combining the perturbation theory and step approximation method is proposed to calculate the proper launching parameter and base trajectory quickly; and an equation of the model parameters which can be calculated by iteration is deduced to fast modeling under arbitrary destination and condition. Simulations and uncontrolled experiment were carried out to verify the feasibility of the proposed method. The results show that the base trajectory and perturbation model can be established. Compared with the modified point-mass trajectory (MPT) method, the predicted error of ascending trajectory of perturbation method is smaller and the predicted error of descending one is larger. Considering the characteristics of PP and MPT methods, a piecewise prediction method combining PP and MPT is proposed. According to the Monte Carlo simulation, the correcting effect of PW method is better than those of PP or MPT method.

ordnance science and technology; guided projectile; rapid impact-point prediction modeling; perturbation theory; base trajectory generation; piecewise prediction method

2016-07-06

國家自然科學基金項目(11402121)

王鈺(1991—)， 女， 博士研究生。 E-mail: 15250996016@163.com

王曉鳴(1962—)， 男， 教授， 博士生導師。 E-mail: 202xm@163.com

TJ413+.6

A

1000-1093(2017)05-0867-10

10.3969/j.issn.1000-1093.2017.05.005