第二類華羅庚域上的極值問題

李海濤,蘇簡兵,王艷永

(1.江蘇師范大學 科文學院,江蘇 徐州 221116;2.江蘇師范大學 數學與統計學院,江蘇 徐州 221116;3.呂梁學院 數學系,山西 呂梁 033000)

第二類華羅庚域上的極值問題

李海濤1,蘇簡兵2,王艷永3

(1.江蘇師范大學 科文學院,江蘇 徐州 221116;2.江蘇師范大學 數學與統計學院,江蘇 徐州 221116;3.呂梁學院 數學系,山西 呂梁 033000)

討論第二類華羅庚域上的一個極值問題.此極值問題可以看作是復平面上經典的Schwarz引理在高維的一個類似,也可以認為是復平面上經典的Schwarz引理在高維的一個推廣.通過計算出第二類華羅庚域的最小外切橢球,得到部分情況下第二類華羅庚域與單位超球間的極值映照和極值.

極值問題; 華羅庚域; 最小外切橢球

多復變函數論中的核心問題之一就是在雙全純映照下域的分類問題.在多復變的理論中,有許多單連通區域是彼此不全純等價的,而證明2個域全純等價就需要采取某種合適的方法.極值問題可以看作是復平面上經典的Schwarz引理在高維的一個類似[1],也可以認為是復平面上經典的Schwarz引理在高維的一個推廣[2].通過極值問題的研究,可以得到把一個域映為單位圓盤的極值映照,并能得到極值距離.利用極值距離,可以來衡量2個域是否雙全純等價.討論的極值問題如下:

設M為Cn中的一個域,p為M中的一個點.假設Mp記為域點對(M,p)(為簡單計,稱之為“點域”),對于2個點域Mp與Nq,記Hol(Mp,Nq)為由所有將M映入N且將點p映為點q的全純映照所組成的集合.對于一個映照f∈Hol(Mp,Nq),如果成立

|detdf(p)|=

則稱f為Carathéodory極值映照,而|det df(p)|稱為Carathéodory極值,分別簡稱為C-極值映照與C-極值.

要研究極值的有關問題,當然很重要的一個問題是關于極值映照和極值的計算問題.在這方面,C.Carathéodory[3]做了開創性的工作,得到了多圓柱到單位超球的極值;后來,Y.Kubota[4-7]用較復雜函數的級數展開分析方法得到了Cartan域到單位超球的極值;關于復橢球與單位超球間的極值和極值映照由Ma D.W.[2,8]所得到.

華羅庚域是Yin W.P.等[9]在對稱典型域的基礎上建立的,是4類典型域的推廣.作為華羅庚域的2個特例超Cartan域和Cartan-Egg域,它們到單位超球的極值和極值映照已經得到一些結果.如第一類超Cartan域到單位超球的極值和極值映照由文獻[9]得到;第二類超Cartan域到單位超球的極值和極值映照由文獻[10]得到;第三類超Cartan域到單位超球的極值和極值映照由文獻[11]得到;第四類超Cartan域到單位超球的極值與極值映照由文獻[12]得到;文獻[13]構造了比超Cartan域更廣的一類Hartogs域,得到了從這類Hartogs域到單位超球的極值和極值映照;第一類Cartan-Egg域到單位超球的極值與極值映照由文獻[14]得到.

對于一般的華羅庚域到單位超球的極值和極值映照的研究目前較少,已知第一類華羅庚域到單位超球的極值和極值映照由文獻[15]得到.本文在文獻[15]所用方法的基礎上,討論了第二類華羅庚域到單位超球的極值與極值映照.

1 預備知識

設Cartan的第二類不可約有界對稱域為RII(p),即

其中,I為p階單位方陣,Z是p階對稱復方陣,即

(1)

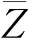
在不引起混淆的情況下不加區分Z和z.

下面給出第二類華羅庚域,其形式如下

其中

N1,N2,…,Nr為正整數,p1,p2,…,pr為正實數.

(2)

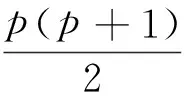
(3)

時,則有

下面記

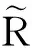
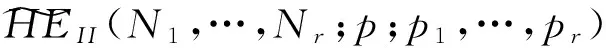
下面定義Hermite橢球.Hermite橢球指形如

的把原點映為原點的全純映射的集合,則Carathéodory極值問題是求一個極值映射

使得

為了給出主要結果,下面給出一些引理.

引理 1.1[2]設D是Cn中包含原點的一個域,Bn為Cn中的單位球,若l是一個復線性映照,使得l(D)?Bn,則l-1(Bn)必為一個包含D的Hermite橢球.如果l是如下極值問題的一個解

則l-1(Bn)必為D的一個具有最小體積的外切Hermite橢球.

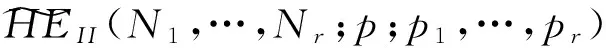
其中,ai>0,b>0(i=1,2,…,r).

由文獻[16]知,對任何p階對稱復方陣Z都存在p階酉方陣Up×p使得

對于任意給定的a1,…,ar,b(ai>0,b>0,i=1,2,…,r),作函數

其中

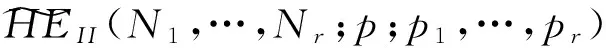
(5)

下的最大值,其中0≤hi≤1,0≤λl≤1,i=1,2,…,r;l=1,2,…,p.

引理 1.3[15]當pi>p(i=1,2,…,r)時,F(h1,…,hr;λ1,…,λp)在(5)式條件下存在唯一駐點并在駐點處取得最大值,其中0≤hi≤1,i=1,2,…,r.

最后,尋求函數

(6)

2 主要結論

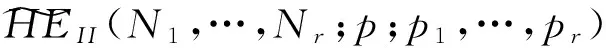
其中

證明 在條件(5)下,求函數(4)的最大值,進而求函數(6)的最小值.下面考慮函數

由

得:

(7)

(8)

(8)式關于l相乘得

(9)

(8)式×(1-λl)相加得

(10)

由(8)～(10)式可得:

(12)

由上述各式可解得:

(13)

(13)式只能當作解出的函數,并無顯示表達.

由引理1.4,令

下面求

的最小值,實際求其最小值點.由文獻[15]知最小值點為其唯一的駐點.

令

(15)

由(5)式(看做ai,i=1,2,…,r,b的函數)對aj(j=1,2,…,r)、b求偏導,并利用(7)和(8)式知:

故(14)和(15)式分別變為:

(16)

由(16)式得

由(17)式得

(19)

(18)與(19)式兩端對應相比得

解之得

(20)

由(16)式及

得

(21)

由(18)式得

(22)

由(20)～(22)式可解出

(23)

再由(12)式進而解出

(24)

(16)和(17)式移項相比并代入(20)和(23)式得

將(24)、(25)式代入(7)式×hj得

由此得

將(24)和(26)式代入(7)式得

(27)

于是根據極值定義、引理1.1及定理2.1可得下面的定理.

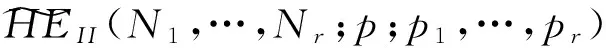
1≤u≤v≤p,

其中,wj=(wj1,…,wjNj),j=1,2,…,r,

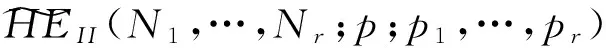
f:HEII(N1,…,Nr;p;p1,…,pr)→

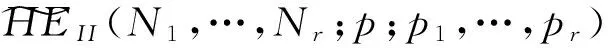
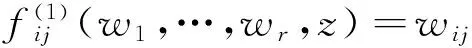
i=1,2,…,r;j=1,2,…,Ni,

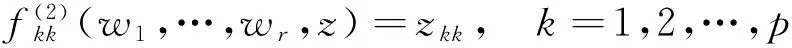
從而可得如下定理.

定理 2.3 當pi>p時,HEII(N1,…,Nr;p;p1,…,pr)到單位超球B的極值映照為:

f:HEII(N1,…,Nr;p;p1,…,pr)→B,

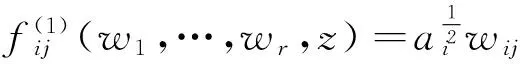
i=1,2,…,r;j=1,2,…,Ni,

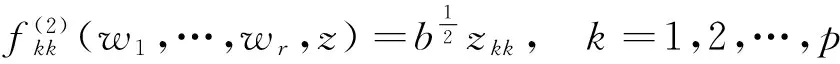
其中,wi=(wi1,…,wiNi),i=1,2,…,r,

于是根據極值定義及定理2.3可得:

定理 2.4 當pi>p時,HEII(N1,…,Nr;p;p1,…,pr)到單位超球B的極值為

其中

[1] TRAVAGLINI G.An analogue of the Schwarz lemma for bounded symmetric domains[J].Proc Am Math Soc,1983,88(1):85-88.

[2] MA D W.Carathéodory extremal maps of ellipsoids[J].J Math Soc Japan,1997,49(4):723-739.

[3] CARATHéODORY C.über die abbildungen,die durch systeme von analytischen funktionen von mehreren veranderlichen erzeugt werden[J].Math Z,1932,34(1):758-792.

[4] KUBOTA Y.An extremal problem on bounded symmetric domains[J].Bull London Math Soc,1983,15(2):126-130.

[5] KUBOTA Y.An extremal problem on the classical Cartan domains I[J].Kodai Math J,1981,4(2):278-287.

[6] KUBOTA Y.An extremal problem on the classical Cartan domains II[J].Kodai Math J,1982,5(2):218-224.

[7] KUBOTA Y.An extremal problem on the classical Cartan domains III[J].Kodai Math J,1982,5(3):402-407.

[8] MA D W.Invariant Metrics on Domains[D].Washionton:Washionton University,1990.

[9] YIN W P,SU J B.Extremal problem on super-Cartan domain of the first type[J].Complex Variables,2003,48(5):441-452.

[10] 趙昕.第二類Cartan-Hartogs域上的極值問題[D].北京:首都師范大學,2006.

[11] 劉知音.第三類Cartan-Hartogs域上的極值問題[D].北京:首都師范大學,2007.

[12] LI H T,SU J B.Extremal problem on super-Cartan domain of the fourth type[J].Acta Math Sin,2008,51(3):541-548.

[13] WANG A,HEUNGJU A,PARK J D.Minimal circumscribed Hermitian ellipsoid of Hartogs domains and an application to an extremal problem[J].Sci China:Math,2009,A52(8):1699-1716.

[14] SU J B,LI H T.The extremal problem on Cartan-egg domain of the first type[J].Chin Quart J Math,2011,26(3):343-349.

[15] SU J B,YIN W P.Extremal problems on the Hua domain of the first type[J].Sci China:Math,2005,A48(S1):343-354.

[16] 陸啟鏗.典型流形與典型域[M].上海:上海科學技術出版社,1963.

[17] 李小飛,王安平,熊良鵬.一類利用Salagean算子定義的解析函數族[J].四川師范大學學報(自然科學版),2013,36(5):678-681.

[18] 秦川,李小飛.一類利用復合算子函數定義的解析函數類的包含性質[J].四川師范大學學報(自然科學版),2015,38(3):376-380.

2010 MSC:32A07

(編輯 余 毅)

Extremal Problem on the Hua Domain of the Second Type

LI Haitao1,SU Jianbing2,WANG Yanyong3

(1.KewenCollege,JiangsuNormalUniversity,Xuzhou221116,Jiangsu;2.SchoolofMathematicsandStatistics,JiangsuNormalUniversity,Xuzhou221116,Jiangsu;3.DepartmentofMathematics,LvliangCollege,Lvliang033000,Shanxi)

In this paper,the extremal problem on the Hua domain of the second type is discussed.The extremal problem can be considered to be similar to the classical Schwarz lemma and also be an extension of the classical Schwarz lemma in high dimension.In some cases,we obtain the extremal mapping and the extremal value between the Hua domain of the second type and the unit ball by determining the minimal circumscribed ellipsoid of the Hua domain of the second type.

extremal problem; Hua domain; the minimal circumscribed ellipsoid

2016-05-25

國家自然科學基金(11171285)

李海濤(1981—),男,講師,主要從事多復變函數論的研究,E-mail:lihaitaolht@163.com

O174.56

A

1001-8395(2017)02-0193-06

10.3969/j.issn.1001-8395.2017.02.009