簇絨地毯織機橫移機構的諧振抑制
郗欣甫, 黃 雙, 孫以澤
(東華大學 機械工程學院, 上海 201620)
簇絨地毯織機橫移機構的諧振抑制
郗欣甫, 黃 雙, 孫以澤
(東華大學 機械工程學院, 上海 201620)
針對簇絨地毯織機高速運行時橫移機構易出現機械諧振,影響橫移系統快速響應和穩定性的問題,在對橫移傳動機構進行理論建模的基礎上設計了校正補償裝置。首先根據橫移傳動系統的階躍響應情況,采用雙T型陷波濾波器消除了橫移傳動系統的機械諧振點。然后使用預變形雙線性逼近法對陷波濾波器進行離散化處理,并且與零階保持器和一階保持器等離散算法進行了實驗對比。結果表明,雙T型濾波器有效地消除了橫移機構高速運行時產生的機械諧振,而且在頻域特性方面,采用預變形逼近法設計的離散陷波濾波器可獲得比零階和一階保持器更加準確的逼近效果。
橫移機構; 校正補償裝置; 諧振抑制; 陷波濾波器; 離散方法
簇絨地毯產品豐富多樣而且生產效率高,市場占有率相比于編織地毯占有壓倒性優勢。近年來國內簇絨地毯產業飛速發展,但與國外仍有較大差距。Tuftco 公司以其獨有的直接高速驅動(DDHS)技術[1]將簇絨地毯織機的工作轉速提升到了2 000 r/min,而國內現有的高端產品只能做到800 r/min。制約簇絨地毯生產效率和產品質量的因素主要有3個:1)耦聯軸系傳動系統以及機架在機器高速運行時產生的振動[2];2)由橫移傳動機構引起的機械諧振和間隙振蕩;3)提花系統喂紗精度以及紗線張力的控制[3-5]。近年來針對簇絨地毯織機橫移系統振動抑制的問題少有研究,但是作為紡織機械制造業的共性難點,在經編機等其他紡織機械設備上已積累了大量的經驗[6-7]。
在機電一體化設備中,傳動部件如傳動軸、滾珠絲杠、聯軸器等都會有一定的彈性,當傳動機構的彈性模態被激發時就會導致機械諧振[8],不僅影響系統運行時的性能和精度,而且對生產設備產生損害,甚至產生不可挽回的損失[9]。針對機械諧振抑制的控制方法主要分為機械和電氣2種控制方案。機械方案立足于機械設計,通過機構優化如動靜平衡、吸能耗能、增大傳動剛度等來降低諧振的影響。機械抑制方案在一定程度上能起到很好的效果,但隨著控制效果和精度的提高,成本也會急速上升。電氣方案又分為主動控制和被動控制2種方式。主動控制通過實時觀測振動狀態和環境干擾,通過特定的高級控制算法主動修改控制器參數實現有效抑制機械諧振的目標[10-11]。主動控制方式不依賴于外部環境的干擾,有很強的穩定性,控制的效果取決于控制算法的選擇和控制器的設計[12-13]。被動控制是針對特定的諧振點設計陷波濾波器以達到消除諧振的目的,這種方法控制參數相對較少,易實現[14]。目前商用伺服系統大都采用被動控制方案將單個或多個陷波濾波器設置于速度環和電流環之間消除特定的諧振點,這樣不僅可降低成本而且也能夠達到令人滿意的效果[8, 15]。
1 簇絨地毯織機橫移機構系統
簇絨地毯織機橫移機構主要由伺服電動機、聯軸器、齒輪、滾珠絲杠和直線導軌組成,主要參數相關定義和數值為:電樞電感L=0.6 H,電樞電阻R=1Ω,轉子轉動慣量J1=10-6kg·m2/rad,轉子阻尼系數D1=10-5N·m·s /rad,電機反電動勢系數Ke=0.186 V·s /rad,電機轉矩常數Kt=0.4 N·m/A,傳動比N=9,傳動機構等效彈性系數K=0.012 N·m/rad,傳動機構等效阻尼系數D12=0.15 cN·s /rad,負載等效轉動慣量J2=0.8 g·m2/rad,負載等效阻尼系數D2=0.004 N·m·s/rad。系統簡圖如圖1所示。
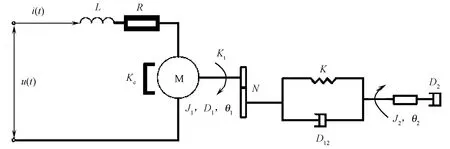
注:u(t)為伺服電動機電樞電壓;i(t)為電動機電樞電流;θ1為電動機轉子的旋轉角度;θ2為負載旋轉角度;M為電動機。圖1 簇絨地毯織機橫移機構等效模型Fig.1 Reduced model of shogging mechanism in tufting carpet loop
根據橫移機構的等效模型,系統參數有如下關系:
(1)
根據式(1)建立系統的狀態方程。設狀態變量x為
(2)
x5=θ2
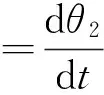
則狀態方程為
(3)
其中:A為系統狀態系數矩陣;B為系統控制系數矩陣;C為輸出狀態系數矩陣;u為控制向量;y為輸出向量。
(4)
根據系統的狀態方程式(3)、(4)和表1中的數值,繪制橫移傳動系統伯德圖(Bode)如圖2所示。
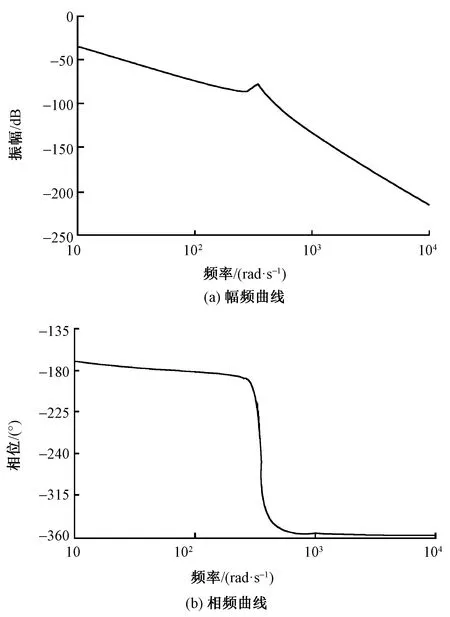
圖2 橫動機構系統Bode圖Fig.2 Bode chart of shogging mechanism. (a)Frequency-amplitude curve; (b)Phase-amplitude curve
由圖2可清楚地得到橫移傳動系統的諧振頻率為351rad/s,即當系統運行在諧振頻率點時設備會產生共振,影響設備的正常運行。
2 校正補償裝置設計
本文通過超前校正裝置來增大系統相角裕度,改善其穩定性,并且可提高截止頻率增強系統的快速性。超前網絡的傳遞函數Gj(s)為
(5)
式中:K為補償裝置增益;τ1、τ2、T1、T2為校正網絡的時間常數;s為復變數。
根據工作要求設定系統階躍響應時間為0.6 s,并且超調量不得大于5%。調用MatLab函數looptune(),可得到式(6):
(6)
將式(6)添加到系統,并驗證校正后系統階躍響應的各項指標是否保持在允許范圍之內。圖3示出系統校正前后的階躍響應。由圖可知,校正后系統響應速度明顯提升,而且系統超調量控制在允許誤差范圍內,與校正前相比更加穩定。
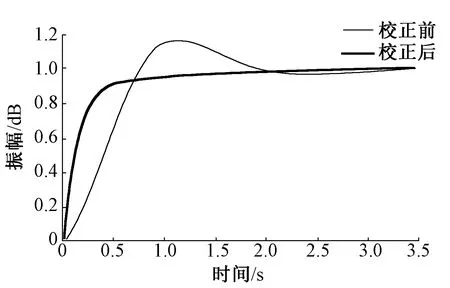
圖3 系統校正前后的階躍響應Fig.3 Step response of system before and after correction
3 雙T型陷波濾波器設計
根據橫移傳動系統的諧振表現,選擇二階傳遞函數GN(S)描述雙T型陷波濾波器,如式(7)所示。
(7)
式中:ζ1、ζ2為陷波濾波器阻尼系數;ωn為系統自然振蕩角頻率,rad/s。
依照工程經驗設定系統穿越頻率為50rad/s,在中頻段的斜率為-30dB/(rad·s-1),并以此整定陷波濾波器的參數,同樣采用MatLab工具箱中looptune()函數進行求解,結果如式(8)所示。
(8)
圖4示出了系統在配置陷波濾波器前后的階躍響應曲線,圖5示出了相應的Bode圖。由圖可看出,陷波濾波器的加入在有效消除諧振點的同時也改善了系統的動態性能。
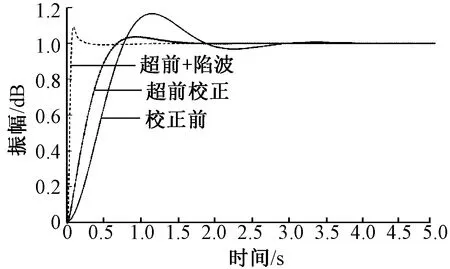
圖4 系統諧波抑制前后的階躍響應Fig.4 Step response of the system before and after resonance suppression
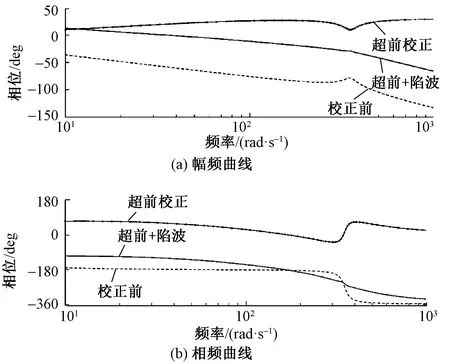
圖5 系統諧波抑制前后的Bode圖Fig.5 Bode chart of system before and after resonance suppression. (a)Frequency-amplitude curve; (b)Phase-amplitude curve
4 陷波濾波器的離散方法
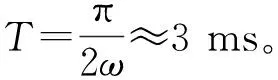
雙線性逼近法(Tustin法)s域和z域的關系如式(9)所示。
(9)
為使Tustin法精確地逼近諧振點,可采用預變形的方式對Tustin法針對特定的頻率點進行修正[16],關系式如式(10)所示。
(10)
選用常用的零階保持器、一階保持器和預變形Tustin法對陷波濾波器進行離散化,通過計算仿真如圖6所示。采用零階保持器和一階保持器都會存在一定的增益和相位裕量畸變,而預變形雙線性逼近法在頻域效果上更加貼近于連續陷波濾波器的控制效果。
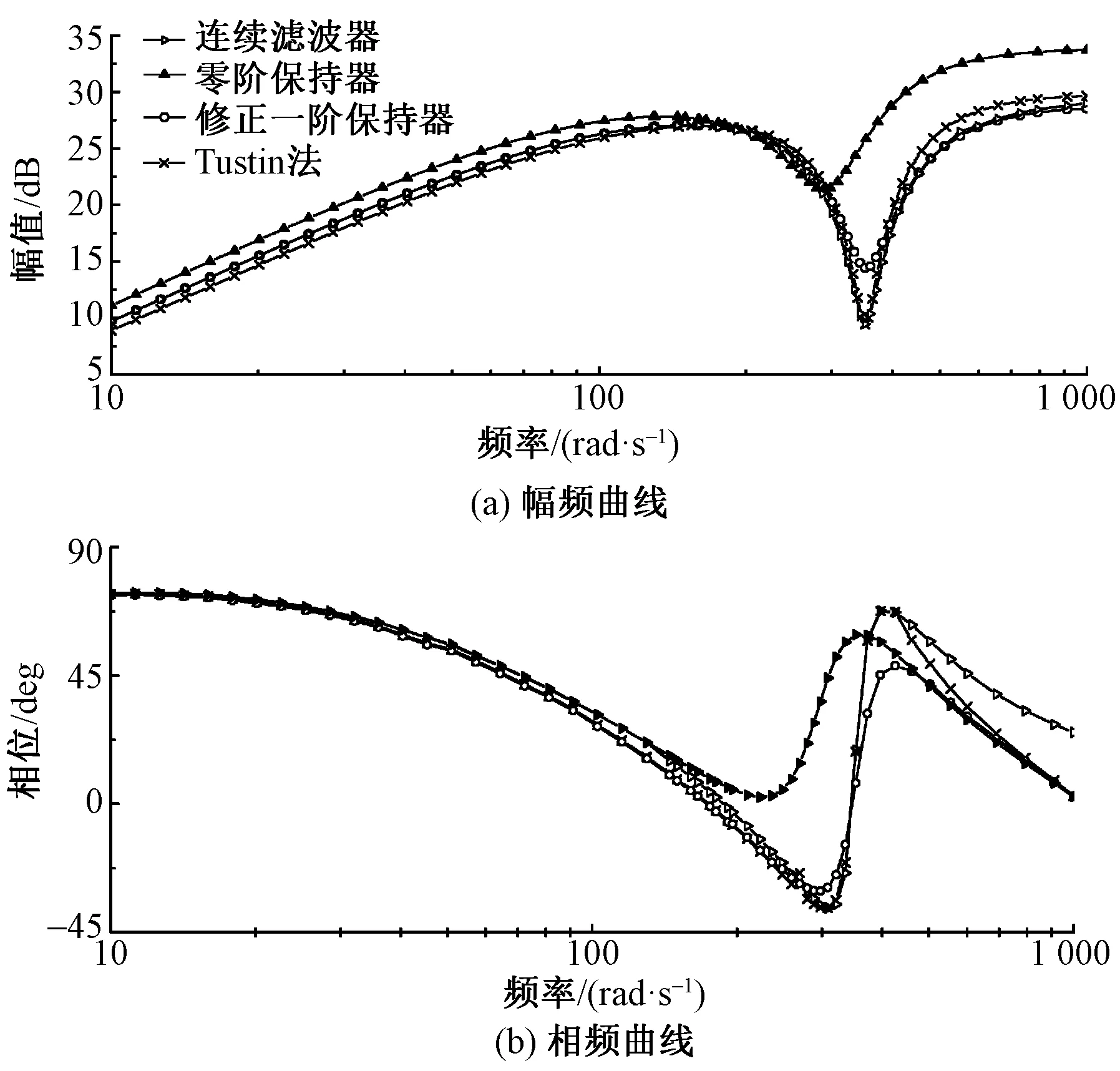
圖6 不同離散方法對陷波濾波器的影響Fig.6 Influence of different discretization methods on notch filter. (a)Frequency-amplitude curve; (b)Phase-amplitude curve
5 結 論
1)簇絨地毯織機橫移系統通過校正補償可提高系統的快速響應性和穩定性。
2)采用不同的離散方法對陷波濾波器的實際增益和相位會產生較大影響,所以要針對實際應用要求選擇恰當的離散方法以達到最佳控制效果。
3)對簇絨地毯織機橫移系統建模,添加校正裝置和陷波濾波器,可有效地提高織機橫移控制系統的動態性能,并為系統設計提供理論參考。
FZXB
[1] MORGANTE M R, BEATTY P E. Tufting machine head shaker:USA,US7578249[P]. 2009-06-01.
[2] 丁彩紅, 楊延竹, 孫以澤. 地毯簇絨機械軸系動力學問題研究的現狀與展望[J]. 紡織學報, 2007,28(8): 120-123. DING Caihong, YANG Yanzhu, SUN Yize. State and outlook of research on shafting dynamics of carpet tufting machine[J]. Journal of Textile Research, 2007,28(8): 120-123.
[3] 丁彩紅, 唐軍. 牽引羅拉穩定紗線張力的作用機制[J]. 紡織學報, 2010,31(2): 110-114. DING Caihong, TANG Jun. Mechanism analysis of yarn tension stabilization using pulling rollers[J]. Journal of Textile Research, 2010,31(2): 110-114.
[4] 夏勝華, 孫以澤, 孟婥, 等. 簇絨地毯織機提花裝置的繞紗動態張力分析[J]. 紡織學報, 2015,36(7): 136-141. XIA Shenghua, SUN Yize, MENG Zhuo, et al, Dynamic tension analysis on winding yarn in jacquard device of tufting carpet machine[J]. Journal of Textile Research, 2015,36(7): 136-141.
[5] 徐洋, 孫志軍, 孟婥, 等. 地毯簇絨系統紗線張力建模與分析[J]. 紡織學報, 2010,31(12): 116-121. XU Yang, SUN Zhijun, MENG Zhuo, et al. Modeling and analysis on yarn tension of carpet tufting ma-chine[J]. Journal of Textile Research, 2010,31(12): 116-121.
[6] 劉念, 夏風林, 張琦, 等. 經編機梳櫛橫移機構的動力學分析[J]. 紡織學報, 2012,33(11): 121-126. LIU Nian, XIA Fenglin, ZHANG Qi, et al. Dynamic analysis of shogging motion mechanism of guide bar on warp knitting machine[J]. Journal of Textile Research, 2012,33(11): 121-126.
[7] 張琦, 夏風林, 劉念, 等. 經編機梳櫛的橫移振動分析[J]. 紡織學報, 2013,34(7): 121-125. ZHANG Qi, XIA Fenglin, LIU Nian, et al. Analysis of shogging motion vibration of guide bars on warp knitting machines[J]. Journal of Textile Research, 2013,34(7): 121-125.
[8] ELLIS G, LORENZ B D. Resonant load control methods for industrial servo drives[C]//OKYAY Kaynak. IEEE Industry Applications Conference. Istanbul: IEEE, 2000.
[9] SZABAT K, ORLOWSKA-KOWALSKA T. Application of the kalman filters to the high-performance drive system with elastic coupling[J]. IEEE Transactions on Industrial Electronics, 2012, 59(11): 4226-4235.
[10] KNYCHAS S, DERUGO P, SZABAT K. Damping of the torsional vibration using adaptive fuzzy control system with different recurrences[C]//KNYCHAS S. Industrial Electronics (ISIE), 2014 IEEE 23rd International Symposium on. Turkey: [s.n.].2014.
[11] PAJCHROWSKI T, ZAWIRSKI K, NOWOPOLSKI K. Neural speed controller trained online by means of modified RPROP algorithm[J]. IEEE Transactions on Industrial Informatics, 2015, 11(2): 560-568.
[12] HACE Ales, JEZERNIK Karel, SABANOVIC Asif, et al. SMC with disturbance observer for a linear belt drive[J]. IEEE Transactions on Industrial Electronics, 2007, 54(6): 3402-3413.
[13] PETER K I B. Robust output-feedback H∞ control With a nonlinear observer for a two-mass system[J]. IEEE Transactions on Industry Applications, 2003, 39(3): 8.
[14] MURPHY B R, WATANABE I. Digital shaping filters for reducing machine vibration[J]. IEEE Transactions on Robotics and Automation, 1992, 8(2): 285-289.
[15] HSU W C, LAI C L, HSU P L. A novel design for vibration suppression for lightly-damped servo control systems[C]//WANG Zidong. 8th Asian Control Conference. Taiwan: IEEE, 2011:251-256.
[16] KORLINCHAK C, COMANESCU M. Discrete time integration of observers with continuous feedback based on Tustin′s method with variable prewarping[C]//LING Nam. 6th IET International Conference on Power Electronics. Xining: IET, 2012:161-161.
Resonance suppression strategy of shogging mechanism in tufting carpet loom
CHI Xinfu, HUANG Shuang, SUN Yize
(College of Mechanical Engineering, Donghua University, Shanghai 201620, China)
Aiming at the problem that the mechanical resonance which influenced the responsiveness and stability of the shogging mechanism was easily induced during the high speed operation of the shogging mechanism on tufting carpet loom, the paper designed the compensation device based on a theoretical model of the shogging mechanism. Firstly, the paper adopted a double T type notch filter to eliminate mechanical resonance points of the shogging driving system, based on the s step response. And then the paper used the Tustin prestressing bilinear approximation method to perform discretization on the notch filter, and compared with the discretization algorithms such as a zero order holder and a first order holder. The results show that the double T type notch filter can well inhibit the mechanical resonance during high speed operation of the shogging mechanism, and the discrete notch filter designed by the Tustin prestressing bilinear approximation method can achieve more accurate approximation effect of the frequency domain characteristics than the zero order holder and the first order holder.
shogging mechanism; compensation device; resonance inhibition; notch filter; discrete method
10.13475/j.fzxb.20160303805
2016-03-21
2016-07-25
國家自然科學基金項目(51375084, 51675094)
郗欣甫(1988—),男,博士生。主要研究方向為紗線力學、多電動機協同控制。孫以澤,通信作者,E-mail:sunyz@dhu.edu.cn。
TS 103.3
A

