一種求解病態復線性方程組的混合算法

陳鳳坤，雷秀仁

(華南理工大學 數學學院，廣東 廣州 510640)

一種求解病態復線性方程組的混合算法

陳鳳坤，雷秀仁

(華南理工大學 數學學院，廣東 廣州 510640)

病態復線性方程的求解是現代應用數學和很多工程應用面臨的難題，用一般算法進行求解時，得到的誤差較大，因此在一些高精度的工程應用上，其結果往往不是特別理想。而隨著科技的發展，現代很多工程應用對數據具有越來越高的精度要求(尤其是國家航天航空)，因此一個能求解病態復線性方程組的高精度算法是很有必要的。從病態復線性方程組求解的特點出發，對模擬退火法進行改進，并將其全局的收斂能力與雙共軛梯度法的高精度求解能力結合起來，提出了一種BCG-SA混合算法。數據實驗表明，模擬退火法能對雙共軛梯度法求出的解進行微調動，幫助雙共軛梯度法在概率意義上跳出局部極小值點，從而提高求解精度。

病態復線性方程組；模擬退火算法；雙共軛梯度法；混合算法；希爾伯特矩陣

0 引 言

求解復線性方程組是很多工程實際應用常遇到的問題，當方程組的規模較大或者系數矩陣的條件數很大時，系數矩陣易呈現病態特性。當前求解病態方程組效果較好的有預處理ILUCG[1]、主元加權迭代法[2]、新Jacobi迭代法[3]、粒子群算法[4]等，但用它們求解病態的復線性方程組的效果不是很理想。目前求解病態復線性方程組效果較好的有雙共軛梯度法，但其存在不收斂或者收斂速度慢的潛在問題，且在搜索的過程中可能陷入局部極小值。

現代很多高科技的工程應用對數據具有越來越高的精度要求(尤其是國家航天航空)，因此一個能求解病態復線性方程組的高精度算法是很有必要的。為此，在分析研究雙共軛梯度算法和模擬退火法的基礎上，根據復線性方程組求解的特點對模擬退火法進行了適當改進，將雙共軛梯度法高精度求解的特性和模擬退火法的全局搜索能力有機結合，提出了BCG-SA混合算法。實驗結果表明，該算法雖然增加了迭代次數，但明顯提高了計算精度，對于一些有較高精度要求的工程應用具有重要的現實意義。

1 雙共軛梯度法(BCG)原理

雙共軛梯度法是C.Lanczos[5]提出的一種用于求解一般復線性方程組的方法，具有計算量少、收斂速度快等優點。在求解規模較大或者條件數較大的復線性方程組時往往效果較好，是目前求解病態方程組較為常用的方法之一。

記(·，·)為通常復內積。若x=(x1,x2,…,xn)T，y=(y1,y2,…,yn)T，xi,yi∈C,i=1,2,…,n，則

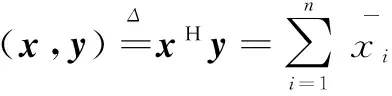
(1)

并記

(2)

考慮如下形式的線性方程組：

Ax=b

(3)

其中，A∈Cn×n，x,b∈Cn。

則具體雙共軛梯度算法[6](算法1)如下：

Step2：計算

并置k=k+1。

Step3：若‖xk+1-xk‖2<ε或k>kmax，則算法終止，轉到Step4,否則轉入Step2繼續計算。

Step4：輸出數值解xk+1和迭代次數k。

2 模擬退火法(SA)原理

模擬退火算法是由N.Metropolis[7]等于1953年提出的，它是基于Monte-Carlo迭代求解策略的一種隨機尋優算法，其出發點是基于物理中固體物質的退火過程與一般組合優化問題之間的相似性。模擬退火算法從某一較高初溫出發，伴隨溫度參數的不斷下降，結合概率突跳特性在解空間中隨機尋找目標函數的全局最優解，是一種通用的優化算法，具有概率性地跳出局部最優解,并最終趨于全局最優的特性。1982年Kinkpatrick等將內能E模擬為目標函數f，溫度T演化成控制參數t，首次將模擬退火算法用于解決組合優化問題。

通過變分原理將式(3)轉化為求解如下無約束條件的多元非線性方程組。

(4)

則模擬退火法應用于求解病態線性方程組的算法(算法2)[8-9]如下：

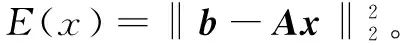
Step2：給x一個擾動x'=x+Δx，其中Δx是整個實軸上服從N(0，σ2)的隨機變量，或者限制當前解的一個鄰域Δx=scale×(rand-0.5)，其中rand是0到1之間的隨機數，計算相應的目標函數值E(x')，得到ΔE=E(x')-E(x)。

Step3：若ΔE≤0，則令x=x'；否則若exp(-ΔE/t)>rand，令x=x',i=i+1。

Step4：若i

Step5：若t

3 混合算法(BCG-SA)

雙共軛梯度法是一種收斂速度快，且精度較高的算法，在實踐中表明雙共軛梯度法的效果非常好，但由于其在搜索過程中可能陷入局部極小值，所以在一些對于數據精度有較高要求的實際應用中，需對雙共軛梯度法進行一些改進，以幫助它跳過局部極小值點。

模擬退火算法[10]具有良好的全局優化性，雖然它在解決病態方程組方面效果不是特別好，但它能夠以隨機搜索技術從概率意義上找出目標函數的全局最小值點。

當雙共軛梯度算法達到較高精度后會出現收斂速度慢或者不再繼續收斂的情況，這表明算法陷入了局部極小值，而模擬退火在搜索過程引入了隨機因素，以一定的概率來接受一個比當前解要差的解，因此有可能跳出這個局部最優解。所以為了得到更高精度的解，可以在雙共軛梯度算法陷入局部極小值時，引入模擬退火法來幫助其跳出局部極小值點。由此受到啟發，將雙共軛梯度法和模擬退火法各自的優點結合起來，提出了混合算法。具體的混合算法(算法3)[11-12]如下：

Step1：輸入矩陣A、右端向量b、誤差精度ε、ε0(ε0>ε),最大迭代次數kmax，SA算法最大調用次數Nmax(不宜設置過大，可取6～10)，置算法迭代次數k=0，SA算法調用次數N=0。

Step3：計算

并置k=k+1。

Step4：若‖xk+1-xk‖2<ε或k>kmax或N>Nmax，則算法終止，轉到Step5；若‖xk+1-xk‖<ε0，調用SA算法，置N=N+1,轉入Step2，否則轉入Step3繼續計算。

Step5：輸出數值解xk+1和迭代次數k。

4 實驗及分析

為了說明算法BCG-SA的有效性和優越性，進行了數據模擬仿真實驗。實驗所用到的矩陣均從經典的病態矩陣演變而來，并且已經證明演變后的矩陣一方面保留了原矩陣的病態性，另一方面擁有復線性，可以代表病態復線性方程組。

將算法BCG-SA與在求解病態方程組上性能優越的共軛梯度法(CG)、預處理共軛梯度法(IC-CG)、雙共軛梯度法(BCG)、預處理雙共軛梯度法(IC-CBCG)、模擬退火法(SA)進行比較。數值實驗結果表明，BCG-SA是有效的且在精度上更優越。需要指出的是進行數值實驗時，也將BCG-SA混合算法與蟻群算法、粒子群算法、神經網絡算法進行了比較，但這些群智能算法的實驗效果并不好，隨著矩陣階數的增加，誤差太大，甚至出現了解的失真。

算例1：考查Hilbert演變矩陣,對于具有病態方程組代表性的Hilbert矩陣B，其中

(5)

令演變矩陣A=B+B*j(j是復數單位，j2=-1),并取方程組右端項b為:

(6)

算例2:考查Pascal演變矩陣，對于具有病態方程組代表性的Pascal矩陣C[13-14]，其中

(7)

(8)

當矩陣的階數n=20時，Hilbert演變矩陣的條件數為1.453 609×1018，Pascal演變矩陣的條件數為8.077 406×1017，已是高度病態的矩陣。實驗時均取初始解x0為零向量，初始溫度Tmax=1 000，Lmax=n(n為矩陣A的階)，最大的試探次數Nmax=8，最低溫度Tmin=1×10-4，鄰域范圍scale=1×10-2，溫度下降因子α=0.9。并在算例1取誤差精度ε=1×10-10，ε0=1×10-12；算例2取誤差精度ε=1×10-11，ε0=1×10-12，實驗結果如圖1和圖2所示(其中IC-CG在求解算例2時失真)。

圖1 Hilbert演變矩陣在不同階數下算法求解誤差的比較

圖2 Pascal演變矩陣在不同階數下算法求解誤差的比較

數據實驗表明：

(1)與BCG-SA混合算相比，蟻群算法、粒子群算法等智能算法在求解高階病態方程組上效果并不理想。

(2)相比于算例1，各類算法在求解算例2時能得到更高的精度。

(3)在算例2中，對CG、BCG進行預處理的效果并不理想。

(4)相對于其他算法，混合算法能得到較高精度的解，從而表明引入模擬退火法對于雙共軛梯度法的改進是有效的，它能夠幫助雙共軛梯度法在概率意義上跳過局部極小值點，從而得到較高精度的解。

5 結束語

為了提高病態復線性方程組的求解精度，在研究分析病態復線性方程的特性和求解方法的基礎上，提出了一種高精度混合算法。該算法是在對模擬退火法進行適當改進的基礎上，將雙共軛梯度法高精度求解的能力和模擬退火法的全局搜索能力有機結合。實驗結果表明，提出的混合算法，雖然增加了計算的迭代次數，但明顯提高了計算精度，對于一些對數據有較高精度要求的工程應用具有重要的現實意義。下一步的工作是進一步優化模擬退火算法的參數。

[1] 于春肖，苑潤浩，穆運峰.新預處理ILUCG法求解稀疏病態線性方程組[J].數值計算與計算機應用，2014，35(1)：21-27.

[2] 唐 麗,李鵬飛.主元加權迭代法求解病態線性方程組[J].科學技術與工程，2012，12(2)：381-383.

[3] 孔祥強.病態線性方程組新的Jacobi迭代解法[J].大學數學，2013,29(5)：50-54.

[4] 賀天宇,李國望.病態線性方程組的粒子群算法[J].科技資訊，2012(8)：15.

[5] 張永杰,孫 泰.大型復線性方程組預處理雙共軛梯度法[J].計算機工程與應用,2007，43(36)：19-20.

[6]GarciaN.ParallelpowerflowsolutionsusingabigconjugategradientalgorithmandaNewtonmethod:aGPU-basedapproach[C]//Power&energysocietygeneralmeeting.[s.l.]:[s.n.],2010:1-4.

[7]SteinbrunnM,MoerkotteG,KemperA.Heuristicandrandomizedoptimizationforthejoinorderingproblem[J].TheVLDBJournal,1997,6(3):191-208.

[8]KeikhaMM.Improvedsimulatedannealingusingmomentumterms[C]//Secondinternationalconferenceonintelligentsystems,modellingandsimulation.[s.l.]:[s.n.],2011:44-48.

[9]WangShengli,ZuoXingquan,LiuXueqing,etal.Solvingdynamicdoublerowlayoutproblemviacombiningsimulatedannealingandmathematicalprograming[J].AppliedSoftComputing,2015,37:303-310.

[10]LinZhenhai.Missionplanningforelectromagneticenvironmentmonitorssatellitebasedonsimulatedannealingalgorithm[C]//28thCanadianconferenceonelectricalandcomputerengineering.[s.l.]:IEEE,2015:530-535.

[11] 鄭洲順，黃光輝，楊曉輝.求解病態線性方程組的混合算法[J].貴州工業大學學報:自然科學版，2008,37(3)：12-15.

[12]BellioR,CeschiaS,GasperoLD,etal.Featuer-basedtuningofsimulatedannealingappliedtothecurriculum-basedcoursetimetablingproblem[J].Computers&OperationResearch,2016,65:83-92.

[13]SrisangngamP,ChivapreechaS,DejhanK.Evenorderbi-quaddigitafilterusingpascalmatrix[C]//Internationalsymposiumoncommunicationsandinformationtechnologies.[s.l.]:[s.n.],2008:327-330.

[14] 楊勝良.Pascal三角形與Pascal矩陣[J].數學的實踐與認識，2003，33(2)：96-100.

A Hybrid Algorithm of Ill-conditioned Complex Linear Equations

CHEN Feng-kun，LEI Xiu-ren

(School of Mathematics，South China University of Technology，Guangzhou 510640，China)

Solving ill-conditioned complex linear equations is difficult in modern applied mathematics and many engineering application,and it is easy to produce significant error and bad result for general algorithms in some high-accuracy application with a usual algorithm.With the development of science and technology,there is more and more restrictions on data accuracy for modern industry especially space flight and aviation.Therefore,it is necessary and impending to find a high accuracy algorithm for ill-conditioned complex linear equations.According to the characteristics of ill-conditioned complex linear equations,a hybrid algorithm of BCG-SA improved with simulated annealing algorithm has been proposed with the advantages of global convergence and high precision solution for bi-conjugate gradient algorithm.The experimental results show that the hybrid algorithm has promoted the precision of solution for bi-conjugate gradient algorithm which can jump out of the neighborhoods of local minimum points in the sense of probability.

ill-conditioned complex linear equations;simulated annealing algorithm;bi-conjugate gradient algorithm;hybrid algorithm;Hilbert matrix

2016-06-02

2016-09-09 網絡出版時間：2017-03-13

國家基金數學天元基金(B13-B5071130)；國家教育部高校博士點基金(B13-C7070170)

陳鳳坤(1990-)，男，碩士研究生，研究方向為群智能算法；雷秀仁，副教授，通信作者，研究方向為科學與工程計算。

http://kns.cnki.net/kcms/detail/61.1450.tp.20170313.1545.036.html

O24

A

1673-629X(2017)05-0016-04

10.3969/j.issn.1673-629X.2017.05.004