應用穩健馬氏距離評價實驗室間比對能力考核

師耀龍，滕 曼，李 成，吳曉鳳，柴文軒，楊 婧，楚寶臨,付 強

1.中國環境監測總站，國家環境保護環境監測質量控制重點實驗室，北京 1000122.河北農業大學科學技術研究院,河北 保定 071001

應用穩健馬氏距離評價實驗室間比對能力考核

師耀龍1，滕 曼1，李 成2，吳曉鳳1，柴文軒1，楊 婧1，楚寶臨1,付 強1

1.中國環境監測總站，國家環境保護環境監測質量控制重點實驗室，北京 1000122.河北農業大學科學技術研究院,河北 保定 071001

基于穩健馬氏距離的多元統計算法，綜合評價了全國環境監測系統96個實驗室4種有機氯農藥監測能力考核的結果，從中篩選出25個考核結果存在異常的實驗室。將多元統計結果與穩健Z比分數結果進行比較，發現基于穩健馬氏距離篩選出的異常實驗室其穩健Z比分數結果也存在一定的問題。同時簡單介紹了穩健馬氏距離及其相關的異常值篩選的算法原理，并詳細介紹了其基于R語言的實現過程。

多元穩健統計；穩健馬氏距離；實驗室間比對；能力考核

環境監測實驗室能力考核是中國環境監測總站(以下簡稱總站)組織的利用實驗室間比對的方式考核環境監測實驗室技術能力和質量管理水平的活動。通過實驗室間比對，有助于總站了解領域內實驗室相關監測項目的能力狀況，及時發現和糾正影響檢測水平的影響因素，促進領域內實驗室檢測能力的提高[1-2]。

伴隨著能力考核工作的開展，其數據評價工作中出現了2個主要問題：①一些實驗室在周期內參加了多輪能力考核，或在一輪能力考核中進行了多個樣品的測試，傳統的評價方法主要是對各實驗室逐個項目或逐個輪次的評價[1-2]，如何用一項綜合指標整體評價實驗室能力尚待研究；②由于能力考核結果不服從或近似服從正態分布，需要對傳統統計量進行穩健化，如果希望整體評價，則需要對其參與的各個項目構成的多元數據進行穩健統計，而穩健Z比分數和迭代法都是對能力考核的一元數據進行穩健統計的方法[3]，對能力考核的多元數據進行穩健統計的方法尚待研究。

鑒于此，研究詳細討論了穩健馬氏距離在有機氯監測能力考核結果評價中的應用，并與穩健Z比分數評價結果進行了比較[1-4]。此外，由于馬氏距離與多元數據的穩健統計方法在中國環境監測領域應用較少，研究對其一般原理與基于開源軟件(R)的實現方法進行了詳細介紹。

1 一般馬氏距離

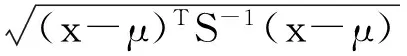
在能力考核多元數據處理中，馬氏距離具有：①不受不同項目之間量綱不同的影響，所得距離為標準化距離；②計算過程考慮到了各項目之間相關性的存在，是建立在總體協方差矩陣上的標準化距離。馬氏距離已應用于包括環境監測領域在內的各個領域內多元數據異常值篩選工作中[6]。但是，傳統的統計方法中，異常值的存在會顯著影響中心值和協方差矩陣的估計，使一般馬氏距離不能正確反映各個觀測的偏離程度。對于這類數據，需要通過穩健統計的方法，構建穩定的均值和協方差矩陣統計量。

2 穩健馬氏距離及其相關R程序包介紹

開源R軟件中的“robustbase”程序包[7-8]中的covMcd程序是基于Fast-MCD算法和PISON等人在2002年的改進完成的[7, 9-11]，廣泛用于估計多元樣本中的穩健統計量。其算法原理較為復雜，可簡單的概括為從樣本中選擇h個觀測，通過不斷的迭代計算h個觀測最小的協方差行列式，該協方差矩陣通過加權即可估計出穩健的統計量，詳細的計算方法參見文獻[7,10-12]。穩健估計結束后，以穩健的中心值和協方差，通過馬氏距離計算各觀測向量偏離中心值的穩健馬氏距離，并可根據DM(x)2符合卡方分布的特點，篩選出數據集中的異常值，這一過程可由R軟件中的“mvoutlier”程序包實現[13]。

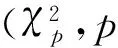
pn(δ)=sup(G(u)-Gn(u))+u≥δ

同時，計算pcrit(δ,n,p)

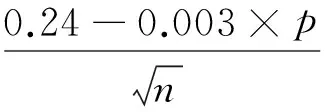
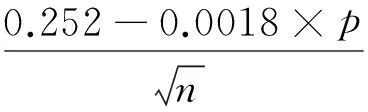
計算完成后，比較pn(δ)和pcrit(δ,n,p)，若pn(δ)pcrit(δ,n,p)，則在其尾部有pn(δ)×100%個異常值(從穩健馬氏距離最大的觀測算起)。

“mvoutlier”程序包同時支持多種計算和畫圖功能，并能從單個變量觀測整個數據集，分析哪些變量更容易導致異常值的出現，可用于能力考核中不合格站點的篩選與考核項目難易的判斷。

研究將通過穩健馬氏距離在有機氯監測能力考核中的應用實例來介紹穩健馬氏距離在實驗室能力考核中的應用。

3 穩健馬氏距離在環境監測實驗室能力考核中的應用

3.1 數據來源與R軟件計算過程

總站于2013年開展了針對全國各地市環境監測站的有機氯監測能力考核，數據選取了96個實驗室測定的α-六氯環己烷(簡寫為α-666)樣品A、α-666樣品B、γ-六氯環己烷(簡寫為γ-666)樣品A、γ-666樣品B、p, p′-雙對氯苯基三氯乙烷(簡寫為p, p′-DDT)樣品A、p, p′-DDT樣品B、o, p′-雙對氯苯基三氯乙烷(簡寫為o, p′-DDT)樣品A和o, p′-DDT樣品B的含量，構成一個96×8的矩陣，R計算過程如下：

>x<-read.table(file.choose(), header=TRUE, row.names=1)#導入txt格式矩陣

>library(robustbase)#調用robustbase

>library(mvoutlier)#調用mvoutlier>covMcd(x, alpha=0.75) #估計穩健統計量(h=0.75)

>cov(x) #估計一般協方差

>apply(x, 2, mean) #估計一般中心值

>res1<-dd.plot(x, quan=0.75) #計算一般馬氏距離和穩健馬氏距離

>mdc<-res1$md.cla

>write.table(mdc, file="classical_md.txt")#保存一般馬氏距離

>mdr<-res1$md.rob

>write.table(mdr, file="robust_md.txt")#保存穩健馬氏距離

>res2<-aq.plot(x, quan=0.75, alpha=0.05)#篩選不合格機構

>outliers<-which(res2$outliers==T)

>write.table(outliers,file="outliers.txt")#保存不合格機構

>uni.plot(x, quan=0.75, alpha=0.05)#從各個項目觀測整體數據偏離情況

>res1<-covMcd(x, alpha=0.75)

>res2<-arw(x,res1$center,res1$cov,0.05)

>sqrt(res2$cn) #計算判斷點位數據異常的臨界值，若某機構馬氏距離≥該值，則表明該機構能力考核結果偏離中心值較遠，結果存在異常。

>q()

計算完成后，各監測機構測定結果偏離中心值的穩健馬氏距離(robust_md.txt)、傳統馬氏距離(classical_md.txt)和基于穩健馬氏距離檢測得到不合格站點名稱(outliers.txt)的分別儲存在R軟件默認的工作目錄下，將25個不合格機構信息匯總進入原始數據集中進一步匯總分析。

3.2 結果與討論

96家機構8種樣品均值、協方差矩陣、穩健中心值和穩健協方差矩陣見表1～表3。比較穩健與非穩健均值和協方差矩陣后發現，由于94、95、96 3個極值的存在(表4)，嚴重影響了該數據集的均值和協方差。說明通過穩健統計估計出的穩健中心值和穩健協方差矩陣可以排除極值對正確估計數據集統計量的影響，更能體現有機氯能力考核數據的正常分布情況。

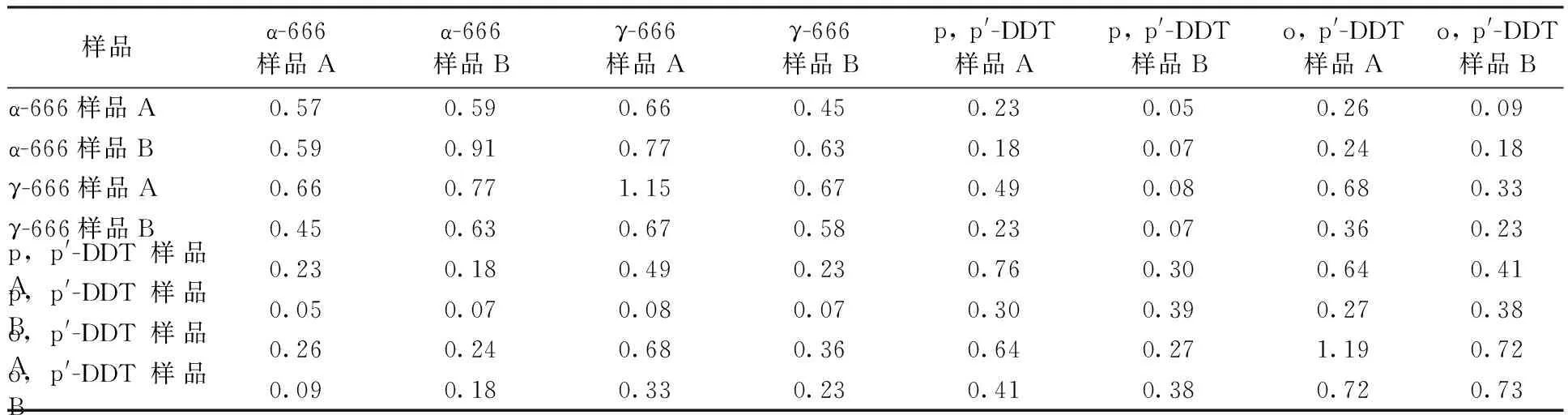
表2 96家監測機構穩健協方差矩陣Table 2 The covariance of 96 labs evaluated by robust multi-statistics

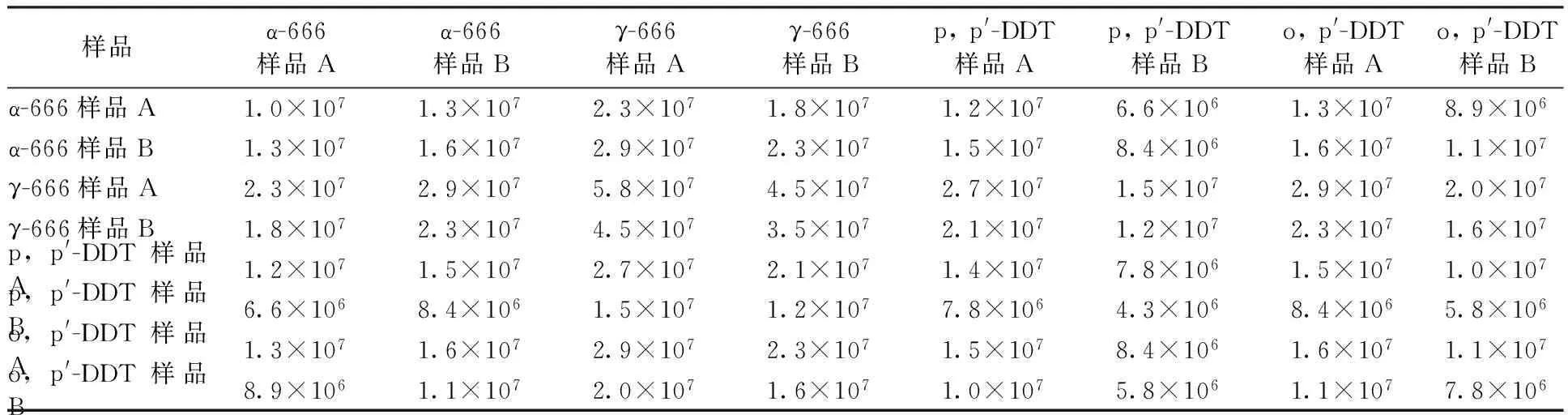
表3 96家監測機構非穩健協方差矩陣Table 3 The covariance of 96 labs evaluated by non-robust multi-statistics

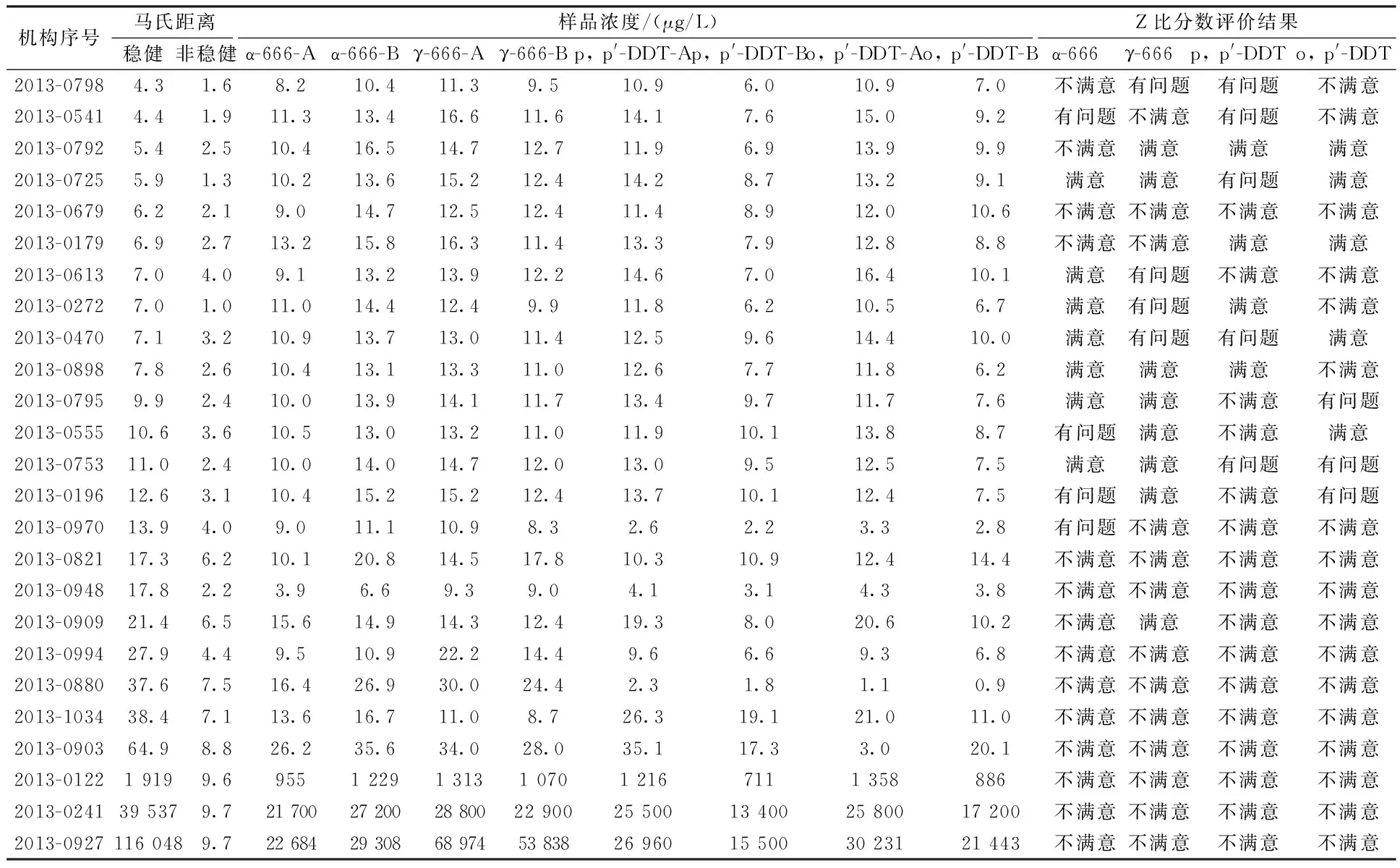
表4 數據異常的25家監測機構穩健馬氏距離、傳統馬氏距離、原始濃度和穩健Z比分數判定結果匯總Table 4 The robust mahalanobis distance, classical mehalanobis distance, concentrations and Z-scores of 25 outlier labs

由表4可見，當置信水平a=0.05時，通過“mvoutlier”程序包計算出該次能力考核判定合格與否的臨界值為4.3，共篩選出25個穩健馬氏距離≥4.3的能力考核結果存在異常的機構(機構名稱用序號表示)。94、95、96站點其濃度值顯著高于其他站點，為明顯的異常值，由于這些極值對中心值和協方差矩陣存在影響，其他機構非穩健馬氏距離明顯小于穩健馬氏距離，表明穩健估計能夠排除極端值對于馬氏距離計算的影響。

穩健馬氏距離越高表明該機構所得結果偏離此次能力考核的中心值越遠，可認為其在此次能力考核中的表現越差(表4)。當根據上文介紹的基于穩健馬氏距離的算法判斷某監測機構能力考核結果為異常值時，說明由于某些分析環節中出現錯誤，或質量體系中存在的一些問題，導致其與其他合格站點數據分布不一致。通過與Z比分數計算出的α-666、γ-666、p, p′-DDT和o, p′-DDT能力考核結果(滿意、有問題或不滿意)進行比較(表4)，發現基于穩健馬氏距離判定出來能力考核結果異常的監測機構其Z比分數結果都存在著不滿意或有問題的項目，說明基于穩健馬氏距離的異常值篩選方法能夠較好地從多元統計的角度發現能力考核中的不合格單位，其結果與Z比分數方法結果較為一致。同時發現，穩健馬氏距離較高的站點，其Z比分數結果存在較多的不滿意或有問題，可以考慮在今后的能力考核工作中根據馬氏距離這一綜合指標來對各個監測機構的整體分析能力做出評估。

4 結論

綜上所述，穩健馬氏距離方法在兼具了馬氏距離的優點的同時，又能較好地排除異常值對其的影響。與傳統的針對單輪次、單項目的穩健統計方法(如Z比分數方法、迭代法)相比，該方法可通過馬氏距離這個單一指標根據多輪次、多項目的能力考核結果從穩健多元統計的角度對實驗室能力或數據質量進行綜合定量評價，并能有效篩選出結果存在問題的監測機構，可以在針對多項目、多輪次能力考核結果的綜合評價工作中加以試用。該方法在實際工作中也存在著一定的局限性，如某些機構在年內只參加了個別輪次的能力考核，或在某輪次的能力考核中只進行部分樣品的分析測試，穩健馬氏距離無法對這些機構該年或該輪次的能力考核結果進行綜合評估。

[1] 滕曼, 付強, 楊婧, 等. 2011年全國環境監測實驗室地表水揮發性有機物檢測能力分析[J]. 環境與健康雜志,2013,30(12):1 108-1 109.

TENG M, FU Q, YANG J, et al. Results analysis of proficiency assessment of VOCs monitoring in water [J]. Journal of Environment and Health,2013,30(12):1 108-1 109.

[2] 滕曼, 付強, 吳曉鳳, 等. 環境監測實驗室水中砷、汞監測能力考核結果評價[J]. 中國環境監測,2014,30(4):183-187.

TENG M, FU Q, WU X F, et al. Results analysis of proficiency assessment of As and Hg monitoring in ground water [J]. Environmental Monitoring of China,2014,30(4):183-187.

[3] 刑小茹, 馬小爽, 田文,等. 實驗室間比對能力驗證中的兩種穩健統計技術探討[J]. 中國環境監測,2011,27(4):4-8.

XING X R, MA X S, TIAN W, et al. Two robust statistic techniques in proficiency testing by interlaboratory comparisons [J]. Environmental Monitoring of China,2011,27(4):4-8.

[4] 吳忠祥. 實驗室能力驗證中的分割水平檢測樣品與穩健統計技術[J]. 中國環境監測,2003,19(4):8-10.

WU Z X. Split-level test sample and robust statistics techniques in laboratory proficiency testing [J]. Environmental Monitoring of China, 2003, 19(4): 8-10.

[5] MAHALANOBIS P C. On the generalized distance in statistics [J]. Proceedings of the National Institute of Sciences (Calcutta),1936(2):49-55.

[6] NORSHAHIDA S, ABDUL A J, MOHDT L, et al.

Anomaly detection and sssessment of PM10functional data at several locations in the Klang Valley, Malaysia [J]. Atmospheric Pollution Research,2015(6):365-375.

[7] ROUSSEEUW P J, VAN D K. A fast algorithm for the minimum covariance determinant estimator [J]. Technometrics,1999(41):212-223.

[8] ROUSSEEUW P J, CROUX C, TODOROV V, et al. Robustbase: basic robust statistics [M].2015.

[9] TODOROV V, FILZMOSER P. An object-oriented framework for robust multivariate analysis[J]. Journal of Statistical Software,2009,32(3):1-47.

[10] PISON G, VAN A S, WILLEMS G. Small sample corrections for LTS and MCD [J]. Metrika, 2002(55):111-123.

[11] HUBERT M, ROUSSEEUW P J, VERDONCK T. A deterministic algorithm for robust location and scatter [J].Journal of Computational and Graphical Statistics,2012(21):618-637.

[12] 王斌會, 陳一非. 基于穩健馬氏距離的多元異常值檢測[J].統計與決策,2005(3):4-6.

WANG B H, CHEN Y F. Multivariate outlier detection based on the robust Mahalanobis distance [J]. Statistics & Decision,2005(3):4-6.

[13] FILZMOSER P, GARRETT R G, REIMANN C. Multivariate outlier detection in exploration geochemistry [J]. Computers & Geosciences,2005(31):579-587.

[14] GERVINI D. A robust and efficient adaptive reweighted estimator of multivariate location and scatter [J]. Journal of Multivariate Analysis,2003(84):116-144.

The Application of Robust Mahalanobis Distance in Proficiency Testing by Interlaboratory Comparisions

SHI Yaolong1,TENG Man1,LI Cheng2,WU Xiaofeng1,CHAI Wenxuan1,YANG Jing1,CHU Baolin1,FU Qiang1

1.State Environmental Protection Key Laboratory of Quality Control in Environmental Monitoring,China National Environmental Monitoring Centre,Bejing 100012,China2.Institute of Science and Technology,Agricultural University of Hebei,Baoding 071001,China

The result of proficiency testing of 4 organo-chlorine pesticide species among 96 enviromental monitoring labs was evaluated by the robust mahalanobis, and 25 labs were identified as outliers by this multi-statistics method. By the comparision between robust mahalanobis distance and Z-score, the outliers identified by robust mahalanobis distance were also indentified as outliers by Z-score. In addition, the fundamental and R implementation of outliers detection by robust mahalanobis distance were described in this article.

robust multi-statistics;robust Mahalanobis distance;interlaboratory comparisions;proficiency testing

2016-03-22;

2016-05-05

國家環保公益性行業科研專項“國家環境監測網環境空氣自動監測(PM2.5、O3) 質量保證與質量控制技術體系研究與示范” (201409011)

師耀龍(1988-)，男，河北保定人，博士，工程師。

楚寶臨

X830.3

A

1002-6002(2017)02- 0127- 05

10.19316/j.issn.1002-6002.2017.02.20