GPS/BDS/GLONASS組合偽距單點定位性能測試與分析

嚴超,余學祥,徐煒,張廣漢

(安徽理工大學 測繪學院,安徽 淮南 232001)

?

GPS/BDS/GLONASS組合偽距單點定位性能測試與分析

嚴超,余學祥,徐煒,張廣漢

(安徽理工大學 測繪學院,安徽 淮南 232001)

本文以高山峽谷地區以及城市建筑群區域GNSS衛星受山體及建筑物遮擋的實際問題為出發點,通過選取不同的衛星方位角模擬不同遮擋環境,研究GPS/BDS、GPS/GLONAS和GPS/BDS/GLONASS組合系統偽距單點定位模型對于單GPS、單BDS系統在不同遮擋環境下的定位精度和三維導航可用性等方面的改善情況。結果表明,組合系統相對于單系統,增加了可見衛星數,降低了PDOP值,當觀測條件不佳時,可以很好地改善定位精度和提高三維導航可用性。

偽距單點定位;可見衛星數;PDOP值;三維導航可用性

0 引 言

隨著美國GPS現代化的建設、俄羅斯GLONASS的大力恢復和我國BDS區域組網的完成和全球組網的建設,GPS、DBS和GLONASS在中國區域以及全球內的聯合定位與導航已成為未來GNSS發展的重要方向[1]。此前眾多學者對GPS/BDS和GPS/GLONASS的研究已取得了豐碩的成果,胡國榮[2]、高曉[3]對GPS/GLONASS和GPS/BDS組合的觀測值定權進行了研究;張輝等[4]對GPS/BDS系統組合的可見性和定位精度進行了仿真;唐衛明等[5]利用實測數據對GPS/BDS系統組合模擬不同遮擋環境下的可見衛星數、PDOP值以及三維導航可用性進行了研究。但對于GPS/BDS/GLONASS系統組合的研究極為有限。李鶴峰等[6]利用實測數據驗證了GPS/BDS/GLONASS組合導航算法的正確性;何俊等[7]根據MGEX網中的13個不同區域的監測站數據,研究了GPS、BDS、GLONASS在全球不同地區的可見性以及組合定位時的隨機模型。

本文以高山峽谷地區以及城市建筑群區域GNSS衛星受山體及建筑物遮擋的實際問題為出發點,編寫了GPS/BDS/GLONASS系統組合定位程序,并采用等權模型、高度角模型以及Helmert模型對組合觀測值進行定權,通過選取不同的衛星方位角模擬不同遮擋環境,研究GPS/BDS、GPS/GLONAS和GPS/BDS/GLONASS組合偽距單點定位模型對于單GPS、單BDS系統在不同遮擋環境下的定位精度和三維導航可用性等的改善情況。

1 GPS/BDS/GLONASS組合偽距單點定位模型

1.1 時空基準統一

GPS、GLONASS和BDS采用的時間基準雖互有差異,但都與世界時(UT)、國際原子時(AIT)以及世界協調時(UTC)存在著密切聯系。任一瞬間GPST 與AIT 間均有一常量偏差(19 s);GLONASST與國際原子時沒有固定的整秒偏差,是不連續的時間系統;BDT與協調世界時UTC(NTSC)的時間偏差小于100 ns[6].但在實際應用GNSS 多模融合導航定位時,以GPST為基礎,將GLONASST與BDT轉化成GPST

GPST=GLONASST星歷+1s×n-19 ,

(1)

BDT=GPST-14s,

(2)

其中:n為 UTC 與 AIT 之間的調整參數,2012年7月1日以后,該調整參數n為35,2015年7月1日以后n為36.

將CGCS2000和PZ90.02坐標歸化到WGS-84坐標下,文獻[8]指出:CGCS2000 和WGS-84 是相容的,在當前的坐標測量精度(1 mm)水平內,CGCS2000 坐標和WGS-84坐標是一致的,可以認為CGCS2000 定位成果同屬于WGS-84 坐標系成果。WGS-84與PZ90.02之間的轉換可以采用布爾薩7參數表示[6]:

(3)

式中: ΔX=-0.47; ΔY=-0.51; ΔZ=-1.56;εx=0.076×10-6;εy=0.017×10-6;εz=1.728×10-6;m=22×10-9.

1.2 數學模型

GPS/BDS/GLONASS組合系統偽距觀測方程可表示為

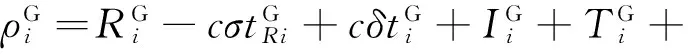
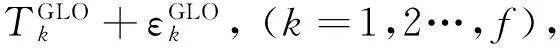
(4)

式中: 上標G,B和GLO分別表示GPS,BDS和GLONASS衛星; 下標i,j和k分別表示GPS、BDS和GLONASS衛星序號;ρ表示衛星與接收機之間的偽距;R表示衛星與接收機之間的幾何距離;δtR表示接收機鐘差;δt表示衛星鐘差;I,T和ε分別表示電離層延遲、對流層延遲和其他誤差;a,b和f分別表示GPS、BDS和GLONASS衛星數量;c表示光速。

將式(4)線性化可得誤差方程:

V=AσX-L,P，

(5)

式中:

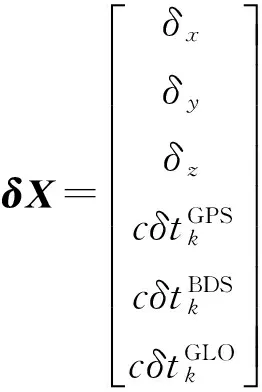
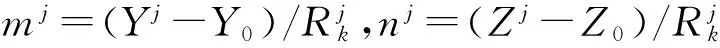
由最小二乘估計可得:

σX=(ATPA)-1ATPL.

(6)

單系統偽距單點定位待估參數有三個坐標分量和一個接收機鐘差,雙系統組合偽距單點定位待估參數有三個坐標分量和兩個接收機鐘差,而三系統組合偽距單點定位待估參數有三個坐標分量和三個接收機鐘差,所以單系統偽距單點定位時至少需要4顆衛星,即必要衛星數為4顆,同理,雙系統偽距單點定位的必要衛星數為5顆,三系統偽距單點定位的必要衛星數為6顆。

本文使用的是GPS的L1、L2頻率、BDS的B1、B2頻率、GLONASS的G1、G2頻率進行偽距單點定位計算,電離層延遲采用雙頻改正模型(無電離層組合);對流層延遲選用簡化Hopfield模型;考慮地球自轉改正和相對論效應。

2 實驗分析

本文數據來源于2016年4月19日在內蒙古自治區鄂爾多斯市的唐家會煤礦基準站(簡稱CTJH站)和監測站(簡稱CTJC站)實測3 h采樣間隔為1 s的GPS、BDS和GLONASS雙頻觀測數據,觀測時間為北京時間2016年4月19日11點20分至2016年4月19日15點00分,CTJH站共11789個歷元,CTJC站共12 840個歷元。兩測站周圍空曠,觀測條件良好。截止高度角設置為10°,根據衛星方位角的選擇模擬多種遮擋環境[5]:

1) 空曠壞境:所有衛星。

2) 遮擋環境:東邊遮擋:剔除方位角在(0°,180°)的衛星;南邊遮擋:剔除方位角在(90°,270°)的衛星;西邊遮擋:剔除方位角在(180°,360°)的衛星;北邊遮擋:剔除方位角在(0°,90°)和(270°,360°)的衛星。

3) 城市街道(峽谷):東西向為方位角在(45°,135°)和(225°,315°)的衛星;南北向為方位角在(0°,45°)、(135°,225°)和(315°,360°)的衛星。

設計方案如下:

1) 方案一:組合系統采用等權模型,相同系統之間采用高度角定權,模擬多種環境。

2) 方案二:組合系統采用高度角模型,模擬多種環境。本文采用的正弦函數模型[9]:

(7)

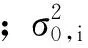
3) 方案三:組合系統采用Helmert模型[3,7,9],相同系統之間采用高度角定權,由于Helmert模型對衛星數量要求較高,所以只模擬了GPS/BDS、GPS/GLONASS和GPS/BDS/GLONASS在空曠環境下的定位情況。

2.1 衛星可見數與PDOP值

圖1示出了兩個測站的GPS、BDS和GLONASS及其組合系統在多種環境下可見衛星數在觀測時間內的平均值。

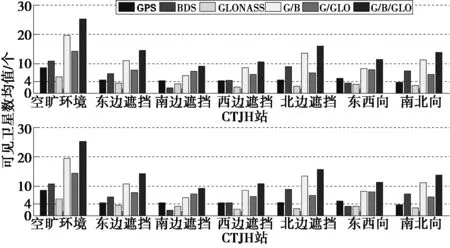
圖1 GPS、BDS和GLONASS系統及其組合系統在各種環境中的可見衛星數均值

圖中:G/B為GPS/BDS的縮寫,表示GPS/BDS組合系統;G/GLO為GPS/GLONASS的縮寫,表示GPS/GLONASS組合系統;G/B/GLO為GPS/BDS/GLONASS的縮寫,表示GPS/BDS/GLONASS組合系統;下文同。

圖1中上、下2幅子圖分別表示CTJH站、CTJC站的GPS、BDS和GLONASS系統及其組合系統在各種環境中的可見衛星數均值。可以看出,空曠環境下,GPS、BDS和GLONASS的可見衛星數均值均超過了單系統偽距單點定位的必要衛星數,且BDS可見衛星數均值比GPS多2顆;不同環境下,組合系統的可見衛星數均值都大于組合系統定位的必要衛星數;當模擬遮擋環境和城市街道(峽谷)時,GPS和GLONASS的可見衛星數均值都大約降至空曠環境下的一半,這是因為GPS和GLONASS衛星都是MEO衛星,在全球范圍內分布較為均勻;當南邊遮擋和在東西向的城市街道(峽谷)時,BDS可見衛星數均值下降到不足4顆,有些歷元無法完成單系統單點定位,這是因為BDS為了在我國實現區域增強采用了GEO和IGSO衛星,而GEO衛星處于赤道上空,在空曠環境下,我國區域內均可見,但我國處于北半球,所以測站南部觀測條件差時,對BDS衛星的可見數就大大減少。

可見衛星數的增加,會形成更好的空間結構,降低PDOP的值。表1示出了不同環境下兩個測站PDOP值在(0,5)范圍的百分比。

表1顯示,無論在何種模擬環境下,三系統所占的百分比要高于雙系統,雙系統高于單系統。空曠環境下,GPS、GPS/BDS、GPS/GLONASS和GPS/BDS/GLONASS的PDOP值都低于5;北邊遮擋時,BDS所占百分比大于GPS,結合圖1,BDS可見衛星數均值與空曠環境相比變化很小,這主要是GEO衛星的功勞;城市街道(峽谷)中,東西向的PDOP值在(0,5)范圍內所在比例要大于南北向,所以東西向的可見衛星比南北向擁有更好地幾何分布。

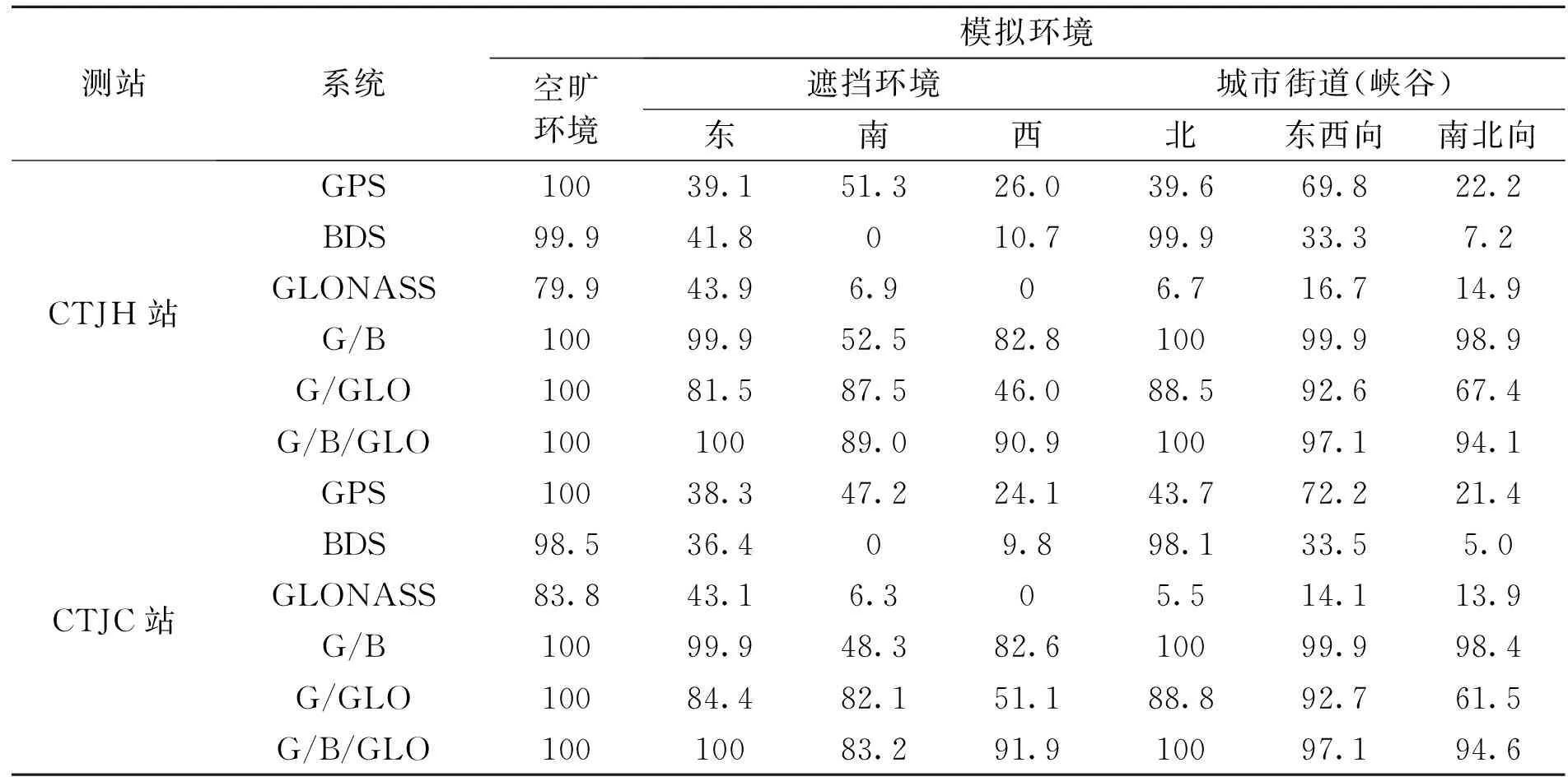
表1 不同環境下PDOP值在(0,5)范圍的百分比/%

2.2 不同隨機模型定位精度和三維導航可用性

本文為了更好地進行精度分析,所計算的定位偏差都是站心直角坐標系下的,主要對三種方案在平面(P)內和高程(U)方向的偏差進行分析,圖2示出了CTJH站三種方案在空曠環境下的定位偏差(CTJC站與CTJH站結論一致),表2示出了空曠環境下兩個測站采用不同方案時平面(P)內定位偏差的RMS值和高程(H)方向定位偏差的RMS值。

由圖2、表2可以看出,空曠環境中,單BDS系統相對于單GPS、GPS/BDS、GPS/GLONASS和GPS/BDS/GLONASS的波動比較大,這是因為BDS衛星測距精度和信號穩定性比GPS略差,且BDS衛星內部不同種星座的測距精度和多路徑效應也有差別;組合系統可以很好地削弱這種波動,使得定位結果更加平滑;而組合系統中,Helmert模型和高度角模型的波動比等權模型更加平滑,Helmert模型和高度角模型在平面(P)和高程(U)方向的偏差都小于等權模型,且Helmert模型和高度角模型精度相當。

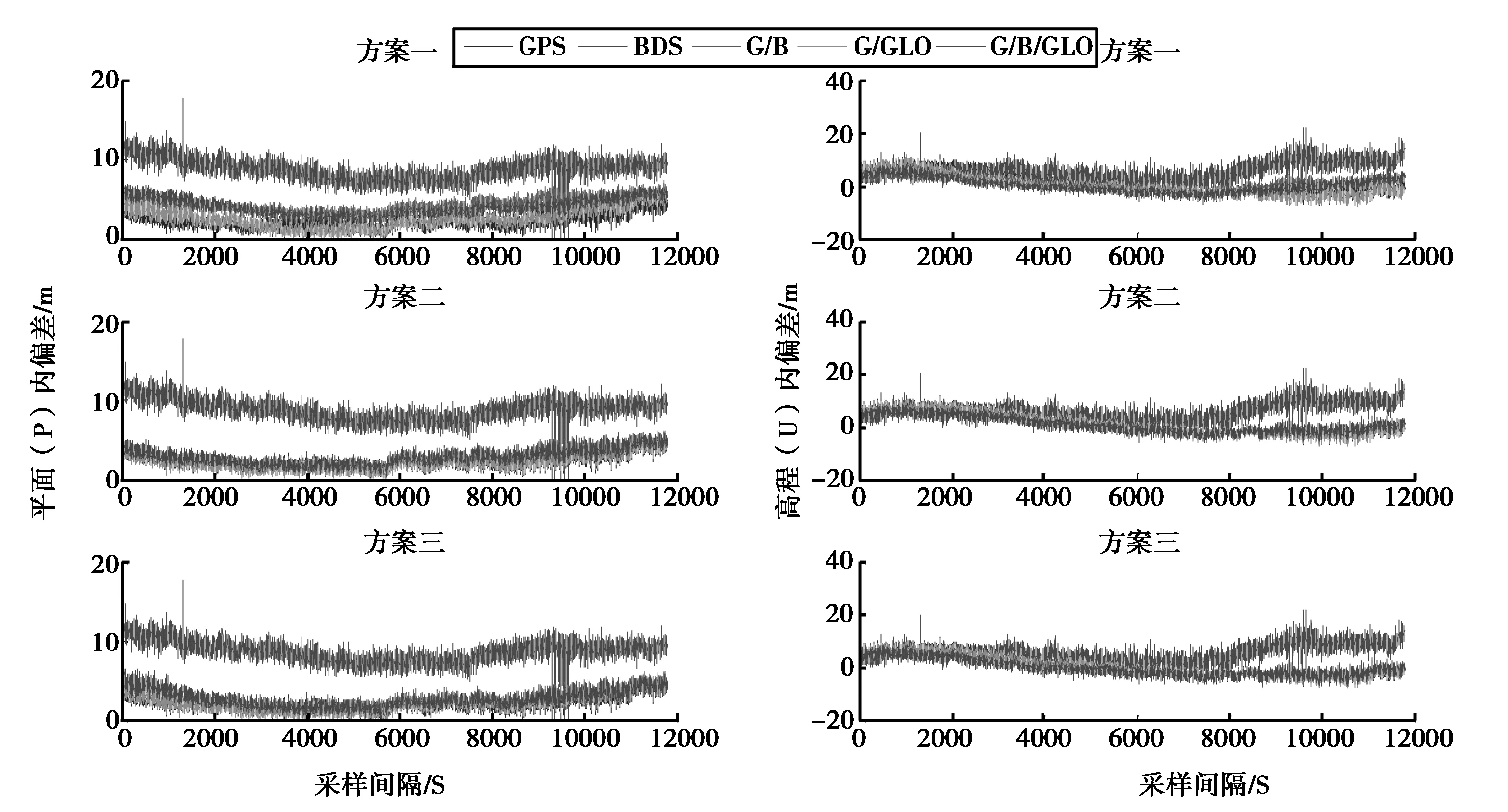
圖2 CTJH站各種方案在空曠環境下平面和高程方向的定位偏差

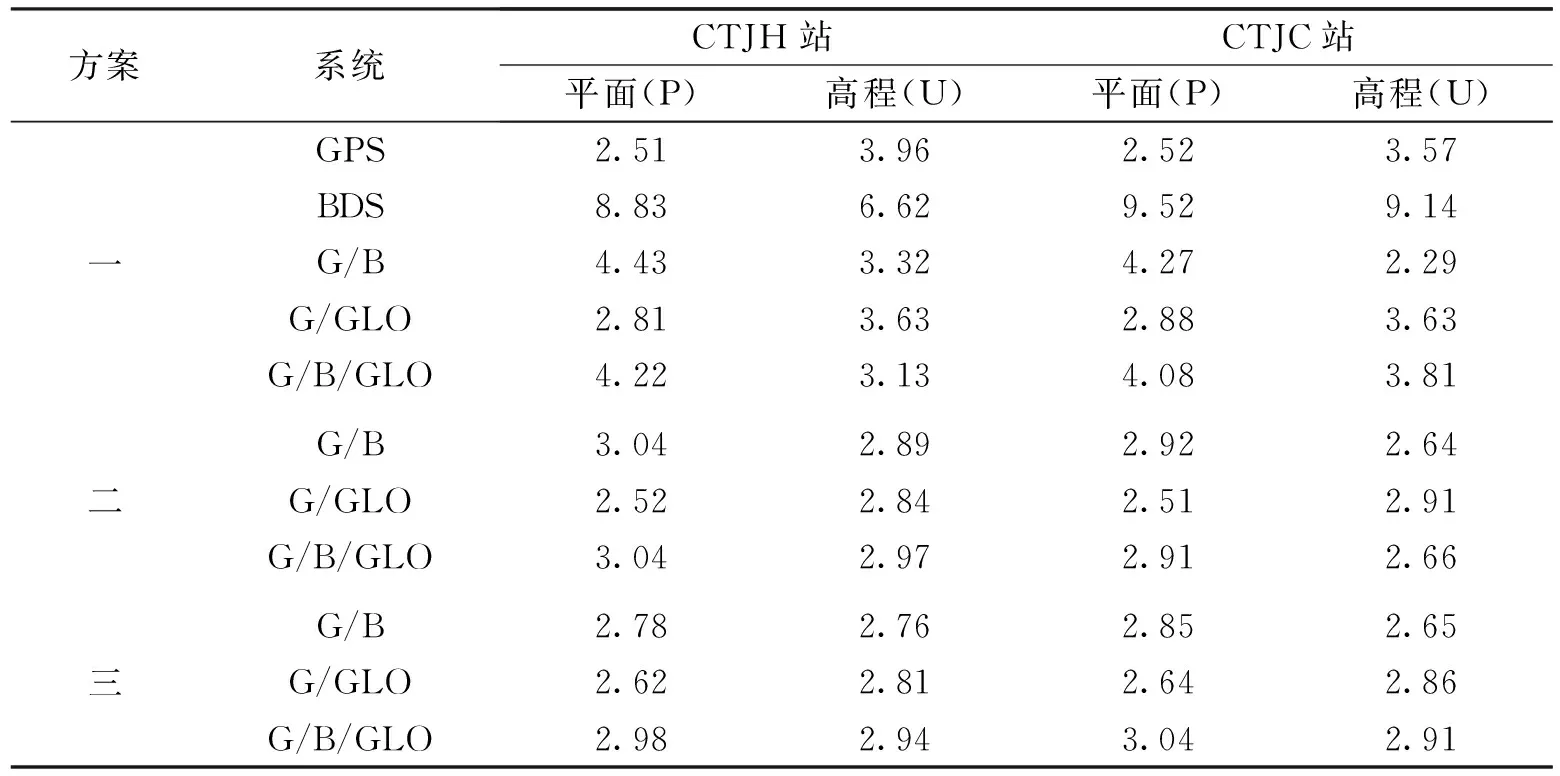
表2 空曠環境下兩個測站的平面(P)內定位偏差的RMS值和高程(H)方向定位偏差的RMS值/m

以CTJH站方案一實驗結果為例,經計算,南邊遮擋時,單GPS系統和單BDS系統在平面(P)和高程(U)方向的RMS值大于100,結合圖1可以發現,單GPS系統和單BDS系統的可見衛星均值分別減少到4顆、2顆,單系統難為達到定位條件,而GPS/BDS、GPS/GLONASS、GPS/BDS/GLONASS組合系統在平面(P)方向的RMS值分別減小到12.5m、5.3m、8.9m,高程(U)方向的RMS值分別減小到12.6m、6.3m、7.8m;北邊遮擋時,單GPS系統在平面(P)和高程(U)方向的RMS值分別為17.4m和15.8m,而單BDS系統在平面(P)和高程(U)方向的RMS值分別為5.8m和9.8m,所以單BDS系統的定位精度要高于單GPS系統的定位精度,結合圖1和表1,這是因為單BDS比單GPS有更多的可見衛星和更優的幾何分布;遮擋壞境和城市街道(峽谷)環境中,組合系統定位精度比單系統定位精度有所提高。按照4個精度等級對等權模型下CTJH站的各種環境的三維導航可用性進行了統計,如表3所示。

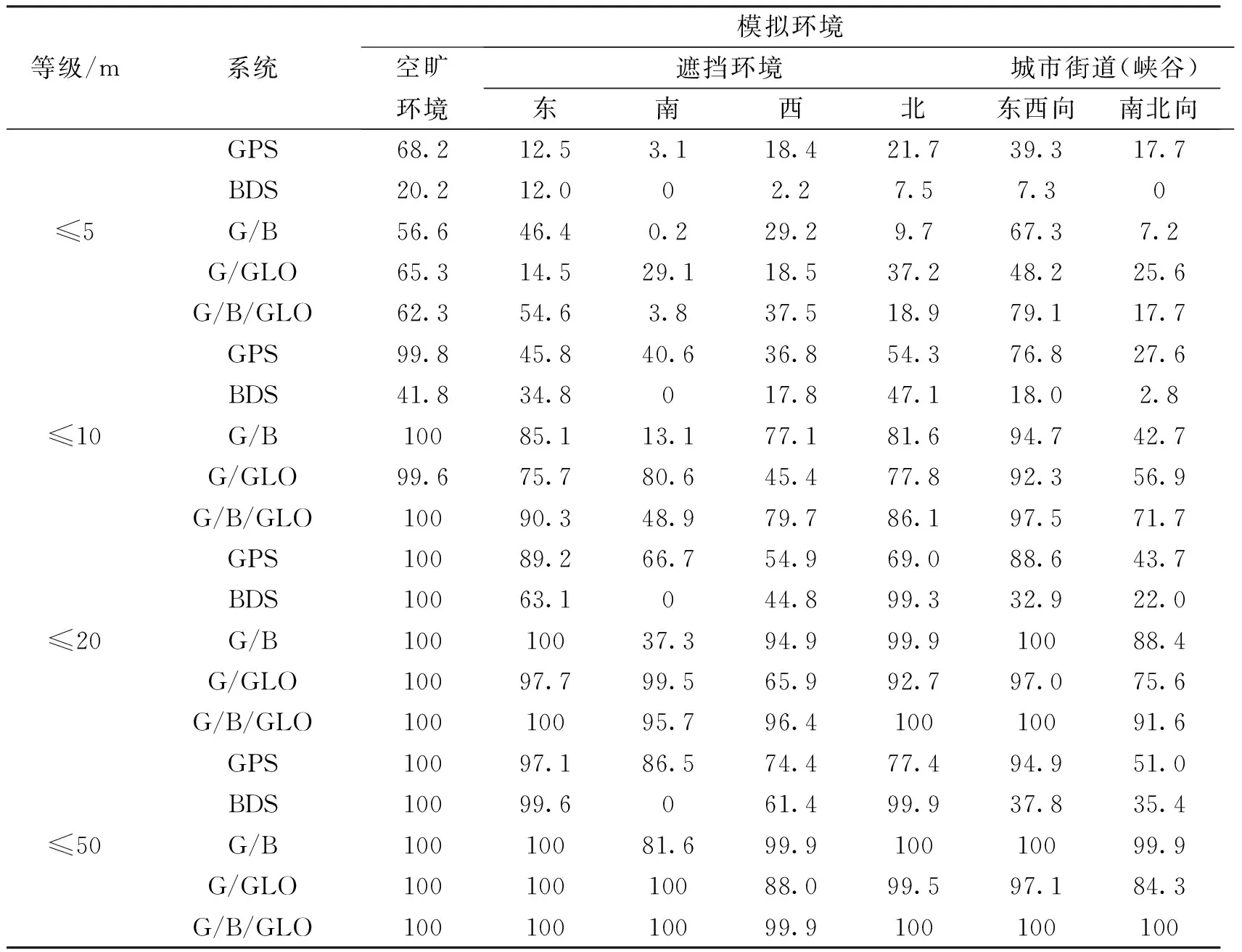
表3 不同遮擋環境中三維導航可用性指標/%

空曠環境下,20m精度內GPS、BDS、GPS/BDS、GPS/GLONASS和GPS/BDS/GLONASS的可用性指標都為100%,但在5m精度內,GPS/BDS/GLONASS的可用性指標要低于GPS和GPS/GLONASS,主要原因是GPS的偽距精度要優于BDS系統和GLONASS系統的偽距精度,BDS系統和GLONASS系統的偽距精度相當,而BDS內部不同種星座的測距精度和多路徑效應有差別。

遮擋環境下,GPS/BDS/GLONASS、GPS/BDS和GPS/GLONASS組合系統對單GPS、單BDS系統的三維導航可用性有了很大地提高。東邊遮擋時,組合系統在20m精度內的可用性指標高達97%以上,而單GPS系統低于90%,單BDS系統低于70%;南邊遮擋時,單BDS系統受到很嚴重的影響,甚至于無法達到定位要求,但GPS/GLONASS和GPS/BDS/GLONASS組合系統在20m精度內可用性指標均能達到95%;西邊遮擋時,GPS/GLONASS、GPS/BDS和GPS/BDS/GLONASS組合系統定位精度都優于單GPS系統和單BDS系統;北邊遮擋時,BDS系統的5顆GEO衛星在中國區域內的區域增強開始發揮作用,單BDS系統在20m精度內的可用性指標高于單GPS系統,南邊遮擋和北邊遮擋對單BDS系統以及GPS/BDS組合系統影響較大;城市街道(峽谷)環境中,東西走向的三維導航可用性指標在同一精度等級中都要高于南北走向,這是因為東西走向的可見衛星有更好的幾何分布;無論何種環境,GPS/BDS/GLONASS組合系統在50m精度內可用性指標都超過了99.9%.

3 結束語

本文以高山峽谷地區以及城市建筑群區域GNSS衛星受山體及建筑物遮擋的實際問題為出發點,通過選取不同的衛星方位角模擬不同遮擋環境,將GPS/BDS、GPS/GLONASS和GPS/BDS/GLONASS組合系統的衛星可見數均值、PDOP值、平面內與高程方向的RMS值以及三維導航可用性指標與單GPS系統和單BDS系統進行對比,得出結論: Helmert模型和高度角模型在平面(P)和高程(U)方向的定位精度優于等權模型,而Helmert模型和高度角模型定位精度相近;城市街道(峽谷)環境中,東西走向的三維導航可用性要高于南北走向,這是因為東西走向的可見衛星有更好的幾何分布;在遮擋環境中,組合系統對于單系統的三維導航可用性指標有很大的提高,GPS/BDS/GLONASS組合系統在50 m精度內可用性指標都超過了99.9%。

[1] 汪亮,李子申,袁洪,等.BDS/GPS/GLONASS組合的雙頻單歷元相對定位性能分析[J].科學通報,2015(60):857-868.

[2] 胡國榮,崔偉宏.組合GPS/GLONASS加權單點定位方法[J].兵工學報,2002,23(1):59-63.

[3] 高曉,戴吾蛟.基于方差分量估計確定GPS/BD2組合定位先驗權比[J].大地測量與地球動力學,2013,33(2):136-138.

[4] 張輝,周田,李博,等.BDS/GPS組合系統定位性能分析[J].測繪科學,2014,39(6):18-21.

[5] 唐衛明,徐坤,金蕾,等.北斗/GPS組合偽距單點定位性能測試和分析[J].武漢大學學報(信息科學版),2015,40(4):529-533.

[6] 李鶴峰,黨亞民,秘金鐘,等.BDS與GPS、GLONASS 多模融合導航定位時空統一[J].大地測量與地球動力學,2013,33(4):73-78.

[7] 何俊,袁小玲,曾琪,等.GPS/BDS/GLONASS組合單點定位研究[J].測繪科學,2014,39(8):124-128.

[8] 魏子卿.2000 中國大地坐標系及其與WGS84的比較[J].大地測量與地球動力學,2008(5): 1-5.

[9] 陳浩,許長輝,高井祥,等.BDS、GPS及其組合系統偽距單點定位精度分析[J].山東科技大學學報(自然科學版),2015,34(2):72-77.

Test and Analysis of GPS/BDS/GLONASS Combined Pseudo-range Point Positioning Performance

YAN Chao,YU Xuexiang,XU Wei,ZHANG Guanghan

(SchoolofGeomatics,AnhuiUniversityofScienceandTechnology,Huainan232001,China)

This paper takes practical problems that mountains and buildings are a shelter from GNSS sateliites in the alpine gorge area and city building area as the starting point,and researches pseudo-range point positioning model of GPS/BDS,GPS/GLONASS,and GPS/BDS/GLONASS combined systems improve the accuracy and usability in three-dimensional navigation comparing with GPS or BDS in different occlusion environment that is simulated by selecting different azimuth. The results show that the combined system compared with the single system, increase the number of visible satellites, reduced the PDOP value.When the poor observation conditions, the combined systems can greatly improve the positioning accuracy and the usability in three-dimensional navigation.

Pseudo-range point positioning; satellite visibility; PDOP; usability in three-dimensional navigation

10.13442/j.gnss.1008-9268.2017.02.006

2016-11-08

國家自然科學基金(批準號:41474026); 淮南礦業(集團)有限責任公司項目(編號:HNKY-JTJS(2013)-28); 安徽省國土資源廳科技項目(編號:2011-K-22;2011-K-18)； 安徽理工大學研究生創新基金(編號：2017CX2056)

P228.4

A

1008-9268(2017)02-0025-07

嚴超 (1993-),男,碩士生,研究方向為GNSS測量與數據處理,礦山變形監測。

余學祥 (1965-),男,教授,工學博士,博士后,博士生導師,主要從事衛星導航定位技術及其應用方面的教學和科研工作。

徐煒 (1992-),男,安徽蕪湖人,碩士生,主要研究方向為GNSS導航與數據處理。

聯系人: 嚴超E-mail:757261684@qq.com