一種基于神經網絡的自適應非線性自動舵

武慧勇，唐勻龍

(1.中國電子科技集團公司第三十八研究所，安徽 合肥 230088；2.孔徑陣列與空間探測安徽省重點實驗室，安徽 合肥 230088)

?

一種基于神經網絡的自適應非線性自動舵

武慧勇1,2，唐勻龍1,2

(1.中國電子科技集團公司第三十八研究所，安徽 合肥 230088；2.孔徑陣列與空間探測安徽省重點實驗室，安徽 合肥 230088)

針對僅航向角可測量的船舶航向控制系統，提出一種基于神經網絡的自適應非線性航向控制器。首先采用神經網絡在線逼近系統中的未知項，并設計滑模觀測器在線估計艏搖角速度；然后基于動態面控制思想設計非線性觀測器-控制器。利用Lyapunov方法證明了誤差變量是一致最終有界的。以某自航船模為例仿真，結果表明所提方法魯棒性好，且操舵合理。

航向控制器；非線性；神經網絡；觀測器-控制器；動態面控制

0 引 言

隨著世界航運業的迅速發展，船舶航向控制一直受到廣泛的關注[1-2]。工程上常用的航向控制方法是比例積分微分(PID)控制，但由于船舶操縱過程具有的大慣性、非線性等特性，會使船舶圍繞期望航線呈周期性偏航運動[1]，從而造成過多的操舵，在存在海浪干擾的情況下，偏航效果更明顯。為提高控制精度，減少偏航，需采用一些先進的控制方法，目前用于船舶運動控制的方法主要有：魯棒控制[3-4]、自適應控制[5]、滑模控制[6]、反步法[7-8]以及基于人工智能的控制方法[9-10]等。其中反步法因其方便構造Lyapunov函數而受到廣泛關注。為了解決反步法對虛擬控制律重復求導的問題，文獻[14]通過引入一階濾波器而避免了對虛擬控制律的直接求導，簡化了控制器設計。文獻[17]則是通過引入二階濾波器避免數值求導。文獻[8]采用的動態面(DSC)思想同樣是通過引入濾波器避免對虛擬控制律直接求導。可見通過引入濾波器可較好地解決反步法中對虛擬控制律重復求導的問題。

神經網絡是估計系統中未知項的有效工具，常用的有徑向基(RBF)神經網絡[6]、單隱層神經網絡[10]等。但是RBF網絡和單隱層神經網絡是靜態網絡，輸入節點較多，且易受噪聲影響。而動態遞歸模糊神經網絡(DRFNN)同時具有遞歸神經網絡和模糊邏輯的優點，它內部包含一個反饋回路，從而可更好地反映系統的動態映射關系[11]。且由于存在內部反饋回路，對于存在微分關系的輸入變量，無需全部作為DRFNN網絡的輸入，從而簡化了網絡的結構，加快了學習速度。

在船舶航行過程中，艏搖角速度受環境干擾的影響較大，有時甚至不可直接測量，因此有必要設計狀態觀測器。文獻[10]采用一種單隱層神經網絡近似估計航向控制系統中的未知非線性函數，并設計觀測器為神經網絡權值更新提供自適應信號，最終設計了船舶航向自適應魯棒控制器。文獻[12]針對航向控制問題，提出了可獨立設計的滑模觀測器和反步控制器，但文中需要已知干擾和建模誤差的上界，而這在實際系統中通常很難確定。

本文針對艏搖角速度不可測量的船舶航向跟蹤控制系統，考慮建模誤差及外部干擾，提出了一種基于動態遞歸模糊神經網絡的非線性觀測控制器。首先基于神經網絡設計了二階滑模觀測器，然后基于動態面控制的思想，利用狀態估計值設計了非線性觀測控制器，并根據Lyapunov定理證明了誤差的一致有界性。仿真表明，本文方法可使船舶快速準確地跟蹤期望航向，且對模型不確定和外部干擾具有良好的魯棒性。

1 問題描述

考慮模型不確定性，船舶航向控制系統的非線性數學模型為[3]：

(1)

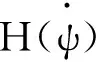
本文設計控制器時考慮舵機系統的特性，船舶舵機特性常用下列模型表示：

(2)

式中：δR為命令舵角，也是本文所設計的控制律；KR為舵機控制增益；TR為舵機時間常數。

定義狀態變量x1=ψ，x2=r，x3=Kδ/T，控制變量u=δR，則由式(1)、式(2)可將船舶航向控制系統的非線性數學模型表示為：

(3)

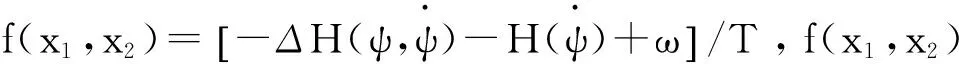
控制目標：對于非線性系統(式(3))，設計控制律u，消除復合干擾的影響，且使x1能穩定跟蹤期望航向ψd。

2 基于神經網絡的觀測器設計

由于艏搖角速度x2的測量受風、浪、流等環境干擾的影響較大，本文將設計二階滑模觀測器對其進行觀測。同時對于復合干擾f(x1,x2)，本文將采用動態遞歸模糊神經網絡進行在線逼近。

2.1 動態遞歸模糊神經網絡

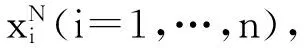
(4)

式中：cij和bij分別為高斯函數的中心和基寬。

第3層為規則層，每個節點代表1條規則，模糊推理運算在這一層進行。同時第3層包含1個內反饋回路，可用來捕獲系統的動態響應而不必在外部添加延時反饋環節。第3層的輸出為：

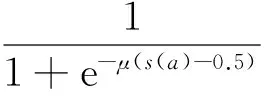
(5)

式中：a=1,…,m；j=1,…,m，m為規則數，且：

(6)

αc,j(k)=αj(k-1)

(7)

(8)

第4層為狀態層，其輸出為第3層推理結果的線性組合，本文取歸一化方式，即：

(9)

由圖1可知，最后一層為第4層輸出的加權和：

(10)

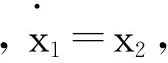
定義神經網絡的參數向量為：

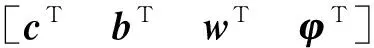
(11)

式中：w和φ分別為第3層和最后一層的權值參數。

根據神經網絡逼近理論可知，存在理想的參數向量θ*，使動態遞歸模糊神經網絡以精度ε逼近未知函數f(x1,x2)，即：

(12)

因此可知f(x1,x2)的神經網絡的估計值為：

(13)

根據式(12)和(13)，并應用泰勒展開，可得神經網絡的估計誤差為：

(14)

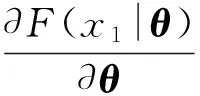
2.2 二階滑模觀測器

在實際中，舵角x3比較容易測量，而艏搖角速度x2受環境干擾的影響較大，不可直接測量。因此本文設計觀測器如下：

(15)

式中：v1,v2為觀測器輸入，分別為[13]：

(16)

式中：σ1,σ2均為正數；sign(·)為符號函數。

由式(3)、(15)和(16)可得，觀測器誤差方程為：

(17)

根據式(15)～(17)即可估計出x2。

設計動態遞歸模糊神經網絡參數向量的自適應律為：

(18)

式中：γ>0；Γ為正定矩陣。

3 基于觀測器的航向控制器設計

3.1 航向參考模型

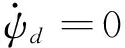
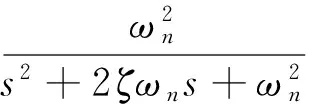
(19)

式中：ψr為指令航向階躍輸入；ζ和ωn為濾波器參數；濾波器輸出ψd為控制系統的參考信號。

3.2 控制器設計

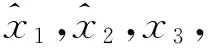
(20)

(21)

為避免下一步中直接對α1求導，使用一階低通濾波器對其進行濾波[15]，濾波器模型如下：

(22)

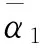
(23)

則將式(23)代入式(21)，得：

(24)

(2) 定義誤差變量z3=x3-α2，選取Lyapunov函數為V2=V1+0.5s2，兩邊求導得：

(25)

設計如下濾波器對虛擬控制律進行濾波：

(26)

(27)

則將上式代入式(25)得：

(28)

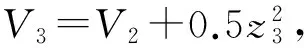
(29)

根據式(29)，設計控制律為：

(30)

4 穩定性分析

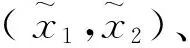
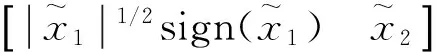
(31)

對式(31)兩邊求導可得：

(32)

根據式(22)和(26)可得：

(33)

(34)

將式(14)、(18)、(29)、(33)、(34)代入式(32)得：

(35)

根據文獻[16]中的引理4.3知，存在κ∞類函數κ11,κ12和κ22,κ22使得式(36)對任意xi∈Rn(i=1,2,3)成立

(36)

對式(35)中耦合項進行不等式放縮得

(37)

(38)

(39)

(40)

(41)

(42)

(43)

將式(37)～(43)代入式(35)得:

(44)

其中:

(45)

(46)

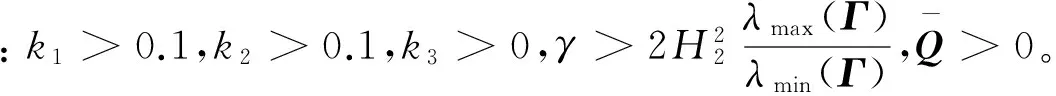
解不等式(46)可得：

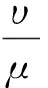
(47)

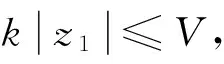
要注意，濾波器(22)和(26)中的濾波時間常數τ1,τ2對系統性能影響較大，一般情況下，可取值0.01～0.03，此時效果較好[14]。

定理1：針對系統(3)，設計觀測器動態方程(15)，采用控制律(30)、觀測器輸入(16)、神經網絡參數向量自適應律(18)，那么選擇合適的參數σ1,σ2,k1,k2,k3,Γ,γ,可使閉環系統中所有誤差信號一致最終有界。

5 仿真驗證

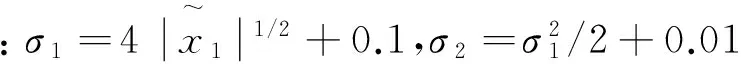
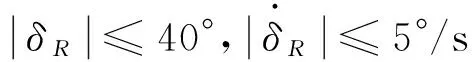
在存在模型不確定及外部干擾時，從圖2可以看出，PID控制無法滿足跟蹤要求，而本文方法精度高、響應快且魯棒性好；圖3和圖4比較了本文方法和未加神經網絡補償的算法。可以看出，未加神經網絡補償時，航向跟蹤誤差出現震蕩，誤差收斂域變大；舵角變化較頻繁，變化幅度較大，且有抖振，這將對船舶舵機的壽命及能耗帶來不利的影響，而本文方法控制舵角光滑且操舵合理，對于實際應用具有重要意義。

圖5和圖6分別為采用本文方法的觀測誤差變化和觀測器輸入曲線，圖7為未加神經網絡補償時的觀測誤差曲線。可以看出，未加神經網絡補償時，觀測誤差明顯變大，這也是導致航向跟蹤誤差變大的主要原因。

6 結束語

針對艏搖角速度不可直接測量的船舶航向跟蹤控制系統，考慮模型不確定及未知外部干擾，提出了一種基于神經網絡的非線性觀測控制器。閉環系統中考慮了舵機響應模型，與實際系統更相符。采用動態遞歸模糊神經網絡在線估計系統中未知項，并設計了二階滑模觀測器對艏搖角速度進行觀測，且設計觀測器參數時，無需已知外部干擾和模型不確定性的上界。然后基于動態面控制的思想，設計了非線性觀測控制器。通過Lyapunov定理，證明了閉環系統所有誤差信號一致最終有界。仿真表明所提方法對于模型不確定和外部干擾具有良好的魯棒性，可使觀測誤差和跟蹤誤差快速收斂，且操舵響應良好，對實際應用具有重要意義。

[1] 張桂臣,任光.不依靠模型自適應控制的船舶自動舵[J].船舶工程,2008,30(1):37-40.

[2] 鄭云峰,楊鹽生,李鐵山.帶有執行機構的船舶航向控制反饋線性化設計[J].大連海事大學學報,2004,30(3):14-17.

[3] 羅偉林,鄒早建,李鐵山.船舶航向非線性系統魯棒跟蹤控制[J].控制理論與應用,2009,26(8):893-895.

[4]ZHANGXK,WANGXP.Concisenonlinearrobustcontrolofcoursekeepingforships[J].ICICExpressLeters,2010,4(4):1263-1267.

[5]KAHVECINE,IOANNOUPA.Adaptivesteeringcontrolforuncertainshipdynamicsandstabilityanalysis[J].Automatica,2013,49(3):685-697.

[6] 肖海榮，李貽斌，周鳳余，韓耀振.基于徑向基函數網絡調節的船舶航向非線性系統滑模控制[J].中南大學學報(自然科學版),2011,42(S1):17-22.

[7]WITKOWSKAA,TOMERAM,SMIERZCHALSKIR.Abacksteppingapproachtoshipcoursecontrol[J].Int.J.Appl.Math.Comput.Sci.,2007,17(1):73-85.

[8] 劉程,李鐵山,陳納新.帶有舵機特性的船舶航向自動舵DSC-MLP設計[J].哈爾濱工程大學學報，2012,33(1):1-6.

[9]HUGS,ZHOUYB,XIAOHR.Applicationoffuzzyneuralnetworkinshipcoursecontrol[C]//AppliedMechanicsandMaterials,2012:309-315.

[10]王志文，彭秀艷.基于自適應輸出反饋的船舶航向控制[J].北京理工大學學報，2011,31(4):425-429.

[11]張平均，蔣新華.基于動態遞歸模糊神經網絡的共振頻率自適應反推控制[J].信息與控制，2011,40(1):21-25.

[12]朱齊丹，周芳，趙國良，包衛衛.基于反步法和滑模觀測器的船舶航向控制[J].華中科技大學學報(自然科學版)，2009，37(4):122-125.

[13]NOLLETF,FLOQUETT,PERRUQUETTIW.Observer-basedsecondorderslidingmodelawsforsteppermotors[J].ControlEngineeringPractice,2008,16(4):429-443.

[14]DUJ,GUOC.Nonlinearadaptivedesignforcourse-trackingcontrolofshipwithoutaprioriknowledgeofcontrolgain[J].ControlTheory&Application,2005,22(2):315-320.

[15]SWAROOPD,HEDRICKJK,YIPPP,GERDESJC.Dynamicsurfacecontrolforaclassofnonlinearsystems[J].IEEETransactiononAutomaticControl,2000,45(10):1893-1899.

[16]KHALILHK.NonlinearSystems[M].ThirdEdition.UpperSaddleRiver,NewJersey:Prentice-Hall,2002:145-146.

[17]FARRELLJA,POLYCARPOUM,SHARMAMetal.Commandfilteredbackstepping[C] // 2008AmericanControlConference.Washington,USA,2008:1923-1928.

A Nonlinear Adaptive Autopilot Based on Neural Network

WU Hui-yong1,2,TANG Yun-long1,2

(1.No.38 Research Institute,China Electronic Technology Group Corporation,Hefei 230088,China; 2.Key Lab of Aperture Array and Space Application,Hefei 230088,China)

Aiming at ship course control system in which only the course angle can be measured,this paper proposes a nonlinear adaptive course controller based on neural network.Firstly the neural network is used to online approach the unknown terms in the system,and a sliding mode observer is designed to estimate the yaw angular velocity online;then a nonlinear observer-controller based on the dynamic surface control idea is designed.According to the Lyapunov approach,all the error variables are proved to be uniformly ultimately bounded.Finally,simulation of a self-propelled ship model is performed,and the result demonstrates that the designed controller has good robustness and the steering gear operation is reasonable.

course controller;nonlinear;neural network;observer-controller;dynamic surface control

2016-11-09

TP273

A

CN32-1413(2017)02-0092-07

10.16426/j.cnki.jcdzdk.2017.02.022