氣囊式液壓蓄能器的數學模型與仿真分析?

畢 超 陳正茂 張立斌 羅松保

?

氣囊式液壓蓄能器的數學模型與仿真分析?

畢 超1陳正茂2張立斌1羅松保1

（1. 北京航空精密機械研究所，精密制造技術航空科技重點實驗室，北京 100076；2. 北京信息高技術研究所，北京 100085）

為了提高液體靜壓導軌系統的動態工作性能，針對其中的氣囊式液壓蓄能器開展了基礎理論研究，通過合理假設和公式推導得到了以氣腔體積為輸出的蓄能器數學模型，并基于此建立了蓄能器的仿真分析模型，考察了蓄能器在不同的充氣壓力下對液壓回路中的階躍沖擊和脈動沖擊的衰減效果，并通過壓力衰減實驗考察了蓄能器對供油管路中的油液波動的衰減規律。實驗結果與仿真結果基本吻合，表明了所建立的氣囊式液壓蓄能器模型的有效性和實用性。

蓄能器；數學模型；液壓系統；傳遞函數

1 引言

近年來，隨著液壓理論與技術的深入研究，基于液壓原理的傳動與控制系統已經廣泛應用于航空航天、工程機械、能源動力和武器裝備等領域。在這些系統中，液壓蓄能器作為一種重要的能量儲存與釋放裝置，可以起到改善液壓系統性能的作用，從而使其穩定、可靠地運行[1]。液壓蓄能器能夠在一定時間內將液壓回路中由動力元件（如油泵等）產生的多余能量轉換成其他形式的能量儲存起來，并將這些能量在執行元件所需能量不足時釋放出來，這樣就使蓄能器具有了蓄積壓力能和吸收壓力沖擊的功能，從而減輕了油路中的壓力波動并提高了能量利用的靈活性[2，3]，因而被廣泛應用于各類液壓自動化設備中。

在各種形式的液壓蓄能器中，氣囊式蓄能器是基于氣體（氮氣）的可壓縮性而研制出的一種液壓蓄能裝置，由于其具有體積小、重量輕、響應快、氣液隔離和易于安裝等特點，并且可以做成不同規格，因而目前應用最為廣泛[4]。具體說來，氣囊式液壓蓄能器主要包括油液部分和氣囊（內部裝有預充壓力的氮氣），當液壓回路中的壓力升高時，油液進入蓄能器，此時氣囊被壓縮，吸收了油液的壓力，從而使回路中的壓力不再上升；而當液壓回路中的壓力下降時，被壓縮的氣囊膨脹，進而將油液壓入回路，從而使回路中的壓力下降得到緩沖[5]。

為了提高Nanosys-1000數控光學超精密加工系統中的液體靜壓導軌的動態工作性能，建立導軌系統中的氣囊式液壓蓄能器的數學模型，并進行了仿真分析與實驗驗證。首先，將蓄能器分為氣腔和液腔兩個部分，分別研究了模型中的各個參數和蓄能器工作參數之間的對應關系；然后建立了蓄能器的仿真模型，主要分析了蓄能器在衰減階躍沖擊和脈動沖擊方面的應用效果；最后，通過實驗考察了蓄能器對液壓回路中的波動壓力的衰減情況，與仿真結果基本吻合。

2 蓄能器的數學模型

如圖1所示，氣囊式液壓蓄能器主要由充氣閥、耐壓殼體、彈性氣囊、菌形閥、進油口和放氣塞等部分組成[6]。其中，彈性氣囊內部的氣腔中裝有預充壓力的氮氣，而液腔通過進油口與液壓回路相通。在氣囊式蓄能器的工作過程中，彈性氣囊內的氮氣主要承受垂直方向的載荷[7]。

圖1 氣囊式液壓蓄能器的基本結構

為了得到氣囊式液壓蓄能器的整體數學模型，首先將蓄能器本體分為氣腔和液腔兩個部分，然后通過受力分析研究每個部分的數學模型，最后再將二者經由相關參數聯系起來。在建立蓄能器的數學模型時，需要做出如下合理假設以簡化建模過程：a.液腔的充液過程較慢，因而可以將氣體壓強和體積的變化近似為等溫過程；b.液腔的放液過程較快，因而可以將氣體壓強和體積的變化近似為絕熱過程；c.氣囊的質量與液腔中的油液質量相比很小，可以忽略，而且氣囊在變形前后的外徑保持不變；d.與氣體相比，油液的壓縮性可以忽略[8]。

2.1 氣腔模型

一般情況下，可以將氣囊中充入的氮氣視為理想氣體（不計粘性的氣體），其狀態可以通過壓強（Pa）、體積（m3）和熱力學溫度（K）進行完整描述[9]。根據理想氣體的數學模型，一定質量的理想氣體的狀態方程為：

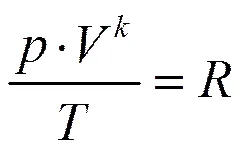
其中，為理想氣體常數；為理想氣體的絕熱指數，對于彈性氣囊內的氮氣而言，可以取=1.41。

在蓄能器液腔的放液過程中，氣腔中氣體的壓強和體積的變化過程近似為絕熱過程，因而此過程中的氣體狀態方程為：

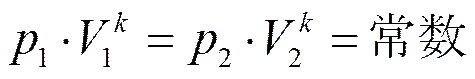
而在蓄能器液腔的充液過程中，氣腔中氣體的壓強和體積的變化過程近似為等溫過程，此時的氣體狀態方程可以通過令式（2）中的=1來得到。當蓄能器充液時，液壓回路中的油液將通過進油口進入液腔，此時彈性氣囊會受到來自液腔的壓力，這樣就會使密封在氣囊中的氮氣被壓縮，其產生的效果類似于彈簧，因而可以將此過程簡化為一個“氣體彈簧-阻尼”模型，如圖2所示。

圖2 “氣體彈簧-阻尼”模型

對彈性氣囊進行受力分析，可以得到氣體的受力平衡方程為：

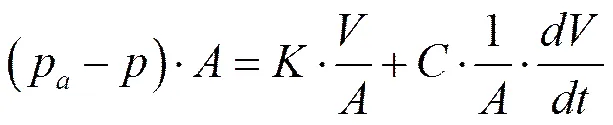
其中，為氣體的剛度系數，N/m；為氣體的阻尼系數，N·s/m；為隔離氣腔和液腔的氣囊面積，m2。在建模過程中，可以將近似取為蓄能器殼體的中間橫截面的面積。

2.2 液腔模型

蓄能器整體的簡化力學模型如圖3所示，將受力對象限定在液腔中的油液上，并設其質量為。

圖3 蓄能器的簡化力學模型

顯然，在不考慮油液的彈性模量時，其受力平衡方程為：

其中，p為蓄能器的進油口壓強；為液腔中的油液質量；為油液的粘性阻尼。

結合式（3）和式（4），可以得到

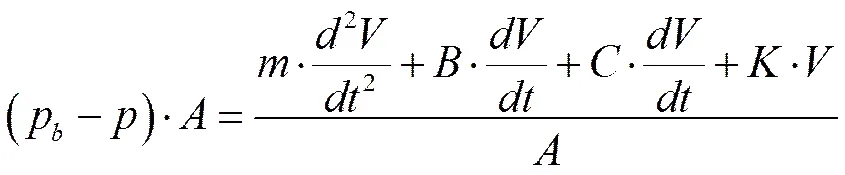
式（5）建立了蓄能器中液腔與氣腔之間的參數關系。設（0，0）為氣腔部分的充氣壓強及其在該工作狀態下的體積，（，）為氣腔部分的任意工作狀態，根據理想氣體的狀態方程（2），有：

（6）

對式（6）在工作點（0，0）處作Taylor展開，并略去高次項，得

將式（6）和式（7）帶入式（5）中，經過整理可以得到以氣腔體積為輸出的蓄能器數學模型，即

（8）

將式（8）轉化為標準形式，得

其中，ω為蓄能器的無阻尼固有頻率：

3 模型參數的確定

3.1 油液等效質量

如果系統的工作壓強為，那么此時系統中氣腔承受的壓強也為，根據式（6），可以得到

其中，為氣腔在系統工作壓強下的體積。因此，可以得到液腔中油液的等效體積Δ為：

（11）

設油液的密度為，則液腔中油液的等效質量為：

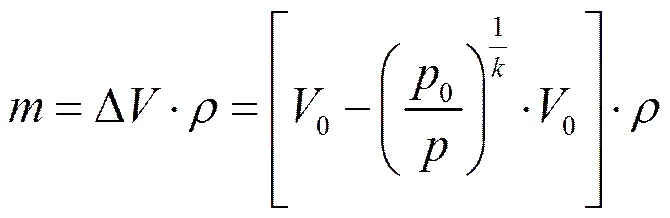
當油液的溫度為50℃時，其密度=855kg/m3。由式（12）可以看出，當蓄能器的工作壓強確定后，液腔中油液的等效質量與氣腔的充氣壓強0呈減函數關系；而當氣腔的充氣壓強0確定后，油液的等效質量與蓄能器的工作壓強呈增函數關系。

3.2 油液粘性阻尼系數

油液粘性阻尼系數的表達式為：

其中，l為蓄能器液腔的等效長度，定義為液腔中油液的總體積Δ與蓄能器殼體的橫截面積的比值，即l=Δ/；為油液的動力粘度，其表達式為

（14）

其中，0為一個大氣壓下的油液的動力粘度（Pa·s），本文取0=0.35Pa·s；為油液的粘壓系數，=0.015～0.035MPa-1，為了方便計算，本文取=0.02 MPa-1。從式（14）可以看出，當蓄能器的工作壓強確定后，油液的粘性阻尼系數與蓄能器氣腔的充氣壓強0之間為減函數關系；而當氣腔的充氣壓強0確定后，油液的粘性阻尼系數與蓄能器的工作壓強之間為增函數關系。

3.3 氣體阻尼系數

氣體的阻尼系數的表達式為：

其中，為氣體的粘度系數，Pa·s。本文取=1.894×10-2Pa·s。從式（15）可以看出，蓄能器氣腔中的氣體阻尼系數與其充氣壓強0呈增函數關系；而當蓄能器的充氣壓強0確定后，氣體的阻尼系數與蓄能器的工作壓強呈減函數關系。

3.4 氣體剛度

在如圖2所示的“氣體彈簧-阻尼”模型中，氣體彈簧的剛度定義為氣體體積的變化量與氣體壓強的變化量之間的比值。因此，氣囊中氣體的剛度表達式為：

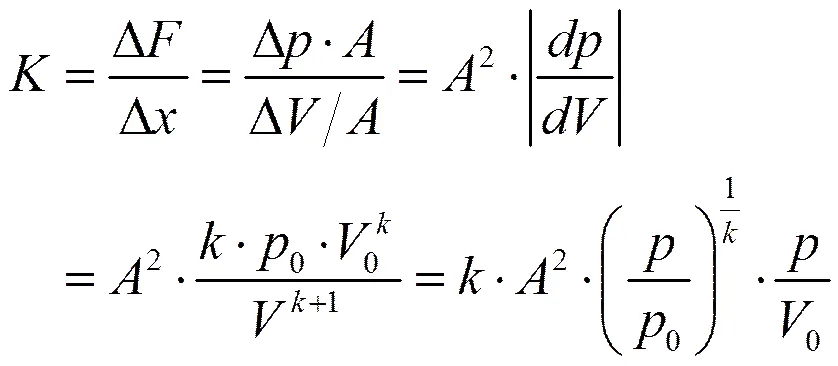
其中，p為密封氣體在某一時刻的壓強，V為密封氣體在該時刻的體積。在本文中，將0和0分別選取為蓄能器的充氣壓強和總容積（也可以認為此時是液腔中無油液時的氣體狀態）。由式（16）可知，當蓄能器和氣腔的充氣壓強0確定后，氣體的剛度隨著系統工作壓強的增大而增大；而當蓄能器及其工作壓強確定后，氣體的剛度隨著充氣壓強0的增大而減小。同時，氣體的剛度與蓄能器總容積0之間為反比例函數關系。

3.5 無阻尼固有頻率和阻尼系數

將式（12）～式（16）分別代入式（9）中，消去模型參數，就可以得到無阻尼固有頻率ω、阻尼系數與系統工況、蓄能器結構參數（如蓄能器殼體的橫截面積）之間的關系，即：

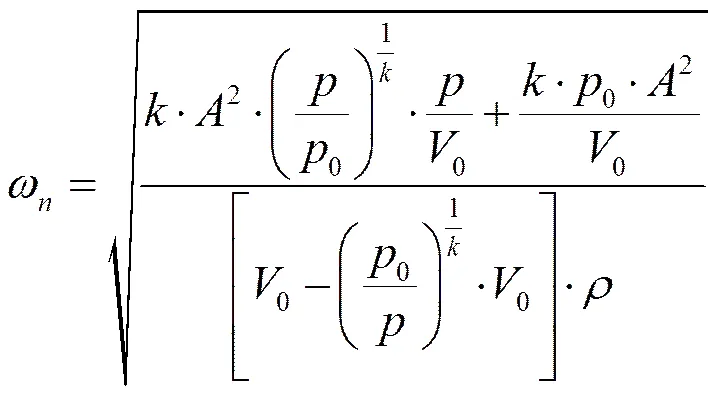
當氣囊式液壓蓄能器用于不同用途時，其參數的選擇要根據具體要求對ω、進行優化，這樣就可以得到蓄能器的相應工作參數。

4 蓄能器吸收壓力沖擊的仿真

在上一節中，建立了以蓄能器的進油口壓強p為輸入信號，以氣腔體積為輸出信號的傳遞函數()。由蓄能器的傳遞函數()可知，其模型為二階系統，本文在Matlab軟件的Simulink集成環境中建立了相應的仿真模型，以考察蓄能器在不同的充氣壓力下對液壓回路中的階躍沖擊和脈沖壓力的衰減情況。

在本文中，氣囊式液壓蓄能器的型號為NXQ-L4，其體積為0.004m3，橫截面積為0.0137m2，系統壓強為1.7MPa，充氣壓強分別為0.6、0.8、1、1.2、1.4和1.6MPa。將其分別代入ω和的表達式中，經計算就可以得到不同充氣壓強下的ω和值，再將這些參數輸入到仿真模型中，并給仿真模型輸入幅值為0.1MPa的階躍信號，就可以得到相應充氣壓強下的蓄能器響應曲線。

如圖4所示，蓄能器在不同的充氣壓強下，對沖擊壓力和脈動壓力的衰減程度不一樣。蓄能器充氣壓強越低，蓄能器對階躍沖擊的衰減程度越高，能衰減80%左右的沖擊壓力；而充氣壓強升高時，其對階躍沖擊的響應時間變短，當充氣壓強為1.6MPa時，其響應時間小于2s。同時，蓄能器對脈動信號也具有類似的衰減效果，其充氣壓強的大小反映出蓄能器對脈動壓力跟隨能力的高低，充氣壓強越高，其跟隨效果越好。綜合蓄能器的衰減效果、響應時間及跟隨能力，在液壓系統的管路中，蓄能器的充氣壓強應該選取工作壓強的0.5～0.6倍，這樣才能最大限度地發揮出蓄能器的功用。

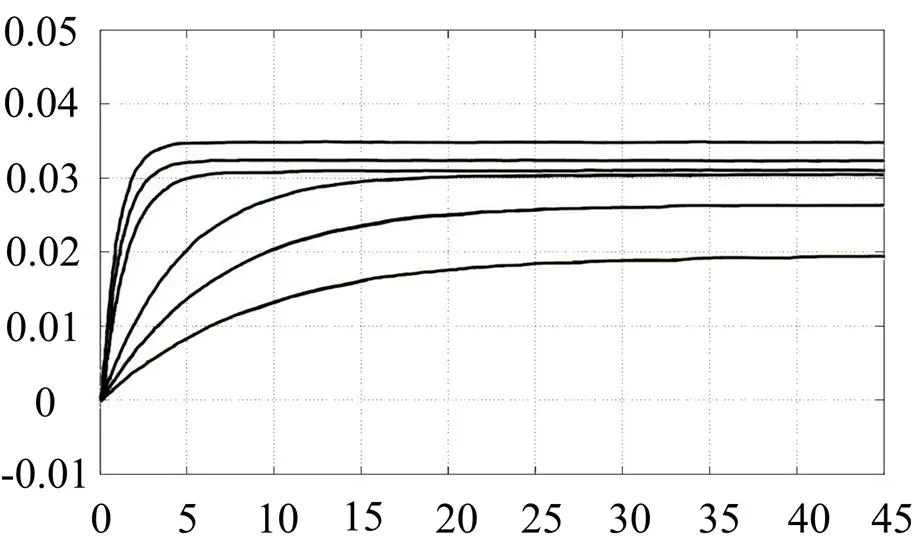
a 消除階躍沖擊的響應曲線

b 消除脈動沖擊的響應曲線

圖4 蓄能器的響應曲線

5 蓄能器的衰減壓力實驗

針對Nanosystem-1000數控光學超精密加工系統的液體靜壓導軌系統的氣囊式液壓蓄能器進行實驗，考察蓄能器對油泵出油口波動壓力的衰減情況。

5.1 實驗現場

由于蓄能器的充氣過程較為繁瑣，因而本文在蓄能器的衰減壓力實驗中，只針對充氣壓強為最佳（0.55倍工作壓強）的情況下實驗。由于只需要考察蓄能器對液體靜壓導軌管路中波動壓力的衰減百分比情況，因而可以采取對液體回路的管壁振動情況進行間接考察的方式，實驗現場如圖5所示。

a 實驗系統???????b 加裝蓄能器???????c 未加裝蓄能器

5.2 實驗結果

對液體靜壓導軌系統的液壓回路振動情況進行信號采集，并對回路中加裝蓄能器和未加裝蓄能器的情況進行對比，所測得實驗數據分別如圖6和圖7所示。

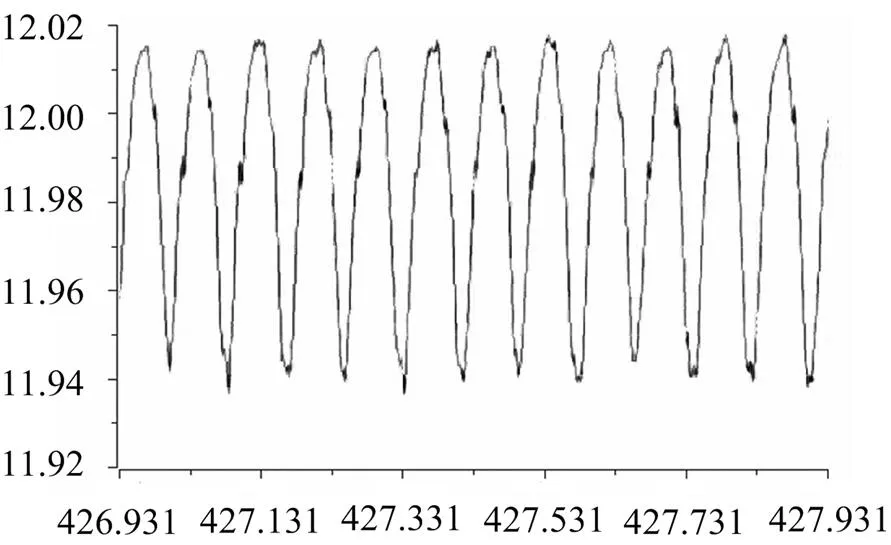
圖6 未加裝蓄能器時回路的振動情況

圖7 加裝蓄能器后的回路振動情況

由圖6和圖7可知，在未加裝蓄能器時，油泵輸出油液時回路的振動峰-峰值為0.081mm；加裝蓄能器之后，輸油回路的管壁振動峰-峰值為0.021mm，衰減了74%的波動壓力。本實驗從間接角度分析了蓄能器對液體靜壓導軌的管路中波動壓力的衰減情況，在最佳充氣壓強的條件下，NXQ-L4型蓄能器可衰減管路中70%的波動壓力，與仿真結果基本吻合。

5 結束語

為了確保Nanosys-1000機床中的液體靜壓導軌的運行穩定性和精度，對其中的重要液壓元件——氣囊式液壓蓄能器進行了數學建模與仿真分析，并實驗驗證。根據蓄能器的結構及工作原理，建立了簡化的蓄能器數學模型，得到了蓄能器的輸入輸出函數，并通過仿真得出了蓄能器在不同的充氣壓強下對液體靜壓導軌系統中的波動油液壓力的衰減情況，仿真結果表明蓄能器的充氣壓強應該選取工作壓強的0.5～0.6倍，以最大限度地發揮出蓄能器的功用。在蓄能器的衰減壓力實驗中，考察了蓄能器對油泵出油口波動壓力的衰減情況，在最佳充氣壓強的條件下，蓄能器可衰減管路中74%的波動壓力，與仿真結果基本一致。

1 張麗飛. 淺談蓄能器制造業的發展現狀[J]. 裝備制造技術，2016(9)：234～236

2 Li Hao, Zhu Yuanhao, Xin Yuhua. Modeling and simulation of a hydro-pneumatic accumulator system for hybrid air development[J]. Applied Mechanics and Materials, 2015, 733(2)：763～767

3 Bao Jiahan, Cen Yuwan, Ye Xiaohua. Researches on the energy regeneration and vibration reduction performance of a new hydraulic energy regeneration suspension[C]. Proceedings of the 6th International Asia Conference on Industrial Engineering and Management Innovation, 2016：605～615

4 孔祥東，權凌霄，姚靜，等. 基于力學分析的蓄能器數學模型建立及實驗研究[J]. 液壓與啟動，2006(7)：31～34

5 李浪，王海濤，龔烈航. 皮囊式蓄能器吸收壓力脈動的參數分析與試驗[J]. 液壓與氣動，2012(7)：3～6

6 于淼，石博強. 液壓制動系統中蓄能器的優化設計與穩健分析[J]. 農業工程學報，2011，27(6)：132～136

7 Wu Xiaoming, Yang Yanfang. Working parameters selection of bladder-type accumulator under the different conditions[J]. Applied mechanics and materials, 2012：841～844

8 Ho T H, Ahn K K. Modeling and simulation of hydrostatic transmission system with energy regeneration using hydraulic accumulator[J]. Journal of Mechanical Science and Technology, 2010, 24(5)：1163～1175

9 史同心. 帶蓄能器差動液壓制動系統油缸壓力分析[J]. 機床與液壓，2016，44(20)：133～135

Mathematical Model and Simulation Analysis of Hydraulic Bladder Accumulator

Bi Chao1Chen Zhengmao2Zhang Libin1Luo Songbao1

(1. Key Laboratory of Science and Technology on Precision Manufacturing Technology, Beijing Precision Engineering Institute for Aircraft Industry, Beijing 100076；2. Beijing Information and High Technology Research Institute, Beijing 100085)

In order to improve the dynamic performance of the hydrostatic guideway system, the basic theory of hydraulic bladder accumulator in it is studied in the paper. Firstly, the mathematic model of the accumulator is established through reasonable assumption and formula derivation, whose output is the volume of the cavity. And then, the simulation analysis model of the accumulator is set up based on the mathematic model, in which the performance of the accumulator in decreasing the pulsatile impact and absorbing the pressure impact is inspected. Finally, the law of attenuating the fluctuation of the hydraulic oil in the pipelines is inspected by experiment, in which the experiment results shown good agreement with the simulation ones. Therefore, the mathematic model of the hydraulic bladder accumulator built up in the paper is effective and practical.

accumulator；mathematical model；hydraulic system；transfer function

“高檔數控機床與基礎制造裝備”國家科技重大專項（No. 2013ZX04001071）。

畢超（1987-），高級工程師，儀器科學與技術專業；研究方向：精密測試技術及儀器。

2016-12-27