面向自動駕駛的動態路徑規劃避障算法

周慧子，胡學敏，陳 龍，田 梅，熊 豆

(1.湖北大學 計算機與信息工程學院，武漢 430062; 2.中山大學 數據科學與計算機學院，廣州 510006) (*通信作者電子郵箱huxuemin2003@163.com)

面向自動駕駛的動態路徑規劃避障算法

周慧子1，胡學敏1*，陳 龍2，田 梅1，熊 豆1

(1.湖北大學 計算機與信息工程學院，武漢 430062; 2.中山大學 數據科學與計算機學院，廣州 510006) (*通信作者電子郵箱huxuemin2003@163.com)

針對自動駕駛中避障的動態路徑規劃問題，提出一種在已知車輛的初始位置、速度、方向和障礙物位置情況下，實時避開障礙物的動態規劃算法。首先,利用三次樣條曲線的二階連續性，結合已知的車道信息產生道路基準線；其次，以車輛的位置方向和道路的曲率構建s-q坐標系，并在s-q坐標系內產生從車輛當前位置到目的位置的一簇平滑曲線，作為候選路徑；最后，綜合考慮車輛行駛的安全性、平滑性和連貫性準則，設計一種新的代價函數，并且通過使代價函數最小化的方法從候選路徑中選擇最佳路徑。在實驗過程中，通過設計多種不同的模擬道路來檢驗算法的性能。實驗結果表明，該方法在多種地形的單車道和多車道道路上都能夠規劃出安全、平滑的路徑，有效避開障礙物，并且具有較好的實時性。

自動駕駛；動態路徑規劃；候選路徑；路徑選擇；代價函數

0 引言

自動駕駛技術作為當今智能交通科技的重要發展方向，可以有效地減少因酒駕、疲勞駕駛、超速等人為操作不當造成的交通事故，還可以改善交通堵塞、提高交通系統總性能[1-3]。動態路徑規劃是自動駕駛汽車信息感知和智能控制的橋梁，也是實現自動駕駛的基礎[4]。動態路徑規劃是按照某一性能指標在其行駛區域內搜索一條從起點到終點的無碰撞的最優或近似最優路徑，其本質是一個具有約束的復雜系統優化問題，在多智能體集群、避障和目標跟蹤控制中都會涉及到，是一個關鍵的基礎共性問題[5-7]，因此，動態路徑規劃和避障對于設計合理的駕駛路徑具有重要意義，不僅規劃結果的優劣影響著自動駕駛汽車的準確性和安全性，規劃算法的復雜度、穩定性也間接影響著汽車的工作效率。

動態路徑規劃技術主要分為兩大類：第一類是全局路徑規劃[6]，它是根據先驗環境模型找出從起點到終點中符合條件的最優或次優路徑，涉及的根本問題是環境模型的表達和路徑搜尋策略；第二類是局部路徑規劃[8-9]，是指在未知或部分未知的環境下通過傳感器獲取周圍環境信息，并使自動駕駛汽車自主獲得一條無碰撞最優規劃的路徑，它側重于考慮車輛當前局部環境信息。本文研究的是局部路徑規劃問題。

目前，局部路徑規劃方法主要有：人工勢場法、啟發式搜索算法和基于離散優化的方法。人工勢場法是將車輛在周圍環境中的運動設計成一種抽象的人造引力場中的運動，目標點對車輛產生“引力”，障礙物對車輛產生“斥力”，最后通過求合力來控制車輛的運動[10]。該方法在數學描述上簡潔、結構簡單、計算量小，但是容易產生局部最優解。啟發式搜索算法主要是A*算法和D*算法[11-12]。A*算法是一種靜態路網中求解最短路徑最有效的直接搜索方法，需要建立環境模型地圖，地圖本身充當了人與車輛互相交流的媒介，這使得操作方便可靠，但是計算量大、耗時長；D*算法是對A*算法的擴充，適合動態環境下的路徑規劃，在動態環境中尋路非常有效，但是它比較復雜，應用范圍有限。基于離散優化的路徑規劃方法是用數值積分和微分等方程來描述車輛的運動，從而產生數量有限的候選路徑，并通過設計代價函數，從候選路徑中選擇最優路徑[13-14]。該方法計算量小，實時性好。文獻[14]提出了一種基于此方法的自動駕駛車輛路徑規劃避障算法，可以為車輛提供最優路徑，但只針對單車道公路或鄉間小路，未考慮城市中的多車道情況。

針對現有局部路徑規劃算法中的容易陷入局部最優、計算量大、未考慮多車道等問題，本文基于離散優化方法，提出了一種新的面向自動駕駛的動態路徑規劃避障算法。該算法能夠在不進行迭代的前提下產生多條候選路徑，并且綜合考慮駕駛的安全性、平滑性和連貫性來設計代價函數，選擇一條最優路徑。實驗結果表明，本文提出的算法不管是對于單車道還是多車道道路，都能夠產生一條最優的路徑，使規劃車輛能夠安全、舒適地繞過障礙物，從起點到達終點，完成路徑的規劃。

1 動態路徑規劃避障算法

本文提出的動態路徑規劃方法是在已知車輛初始狀態信息(包括車輛的位置、車頭方向等)的基礎上，產生一條安全又舒適的行駛路線。本文是在已知全局路線的情況下進行局部規劃，全局路線通過車道級的高精度導航系統獲取。本文中，全局路線由一組道路邊緣的有序點組成。如圖1所示，本文的方法包括三個部分：基準線生成、候選路徑生成和最優路徑選擇。

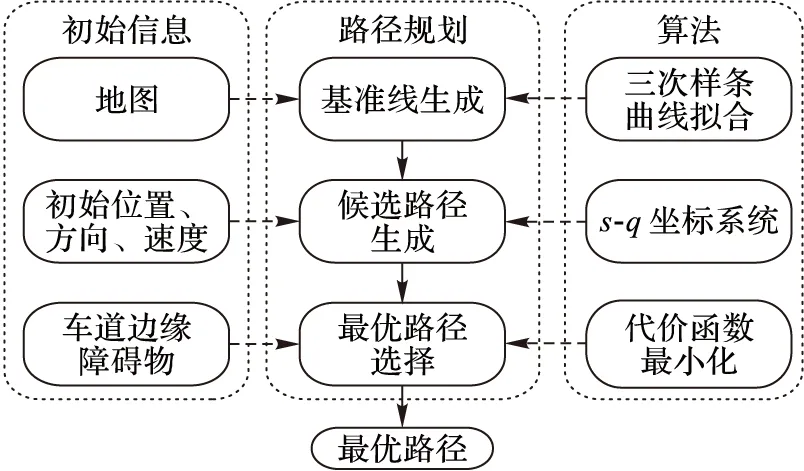
圖1 動態路徑規劃算法流程

1.1 基準線的生成

路徑規劃算法中常用參數曲線來建立道路的集合模型。由于全局路線是一組道路邊緣的有序點，并且考慮到計算曲率時曲線二階導數的連續性，本文采用三次樣條曲線來擬合道路基準線。弧長是最常用的曲線參數，因此采用正交數值法[15]對由道路點擬合成的參數樣條曲線弧長作參數化計算，如式(1)所示：

(1)

如圖2(a)所示，s為車輛當前位置映射在基準線上的弧長，該弧長計算的起點為第i個道路片段的起點si。(xbf,ybf)是曲線上的點在笛卡爾坐標系中的坐標。ax,i、bx,i、cx,i、dx,i、ay,i、by,i、cy,i、dy,i是參數樣條曲線的參數。假設車輛當前位置到基準線上最近的點的距離，即橫向偏移量為q，則車輛當前坐標可以用車輛行駛的弧長s和橫向偏移量q來表示。本文將s和q表示車輛位置的坐標稱為“s-q坐標”。在s-q坐標中，基準線上每個點的切向角θbf和曲率κbf可以用xbf(s)和ybf(s)對s的一階導數和二階導數計算求得，如式(2)所示[14]：

(2)

其中:xbf′、ybf′、xbf″和ybf″分別為xbf(s)和ybf(s)對s的一階導數和二階導數。

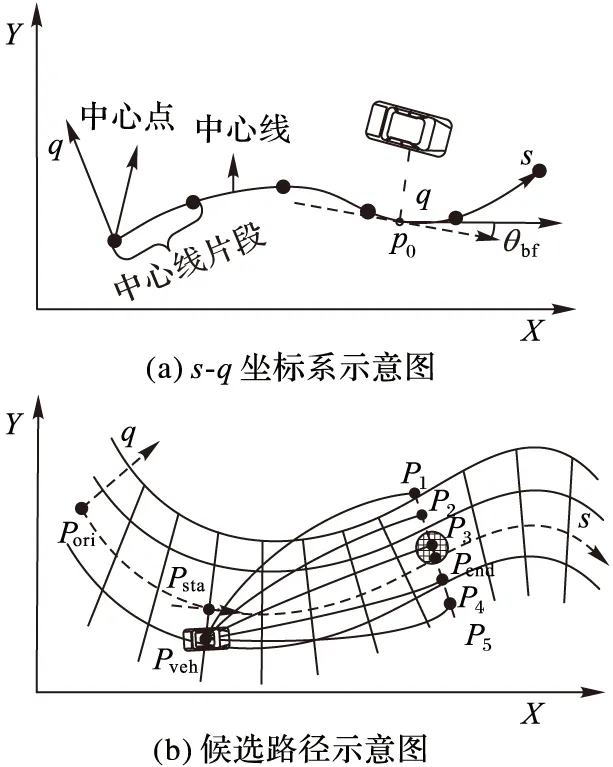
圖2 s-q坐標系與候選路徑示意圖

Fig. 2 Schematic diagram ofs-qcoordinate system and candidate path

1.2 候選路徑的產生

為使用基準線上點的方向角和曲率，有必要找到車輛在基準線上的位置，如圖2(a)所示的p0點。本文利用牛頓拉夫森二次極小化方法找到曲線上最接近車輛位置的點坐標[16]。

如圖2(b)所示，車輛在繞過障礙物時，是否與障礙物碰撞可以用偏移量q來表示。由于車輛行駛的距離是用弧長s表示，因此車輛繞過障礙物的候選路徑可以用橫向偏移量q和弧長s來表示。在s-q坐標系中，假設候選路徑也滿足三次樣條曲線方程，則候選路徑可以用式(3)來表示：

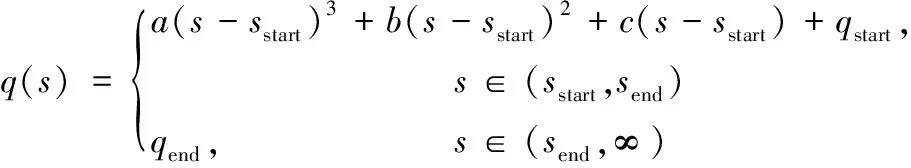
(3)

其中:qstart、qend、sstart和send分別代表本次規劃中候選路徑起點的橫向偏移量、終點的橫向偏移量、起點對應的弧長和終點對應的弧長。為了求解式(3)中的系數a、b、c，本文采用文獻[14]中的邊界條件的方法進行計算。如圖2(b)所示，不同的候選路徑，對應的qend不同，因此，為了獲取多條候選路徑，本文設置N個不同的qend值，分別計算得到N組a、b、c的系數，以此構造出N個式(3)的方程式。由于一個式(3)的方程式表示一條候選路徑，則通過不同qend值可以計算出多條候選路徑。因為候選路徑是在s-q坐標系中計算得到的，而道路和障礙物信息一般都是基于笛卡爾坐標，因此本文采用文獻[14]和[17]描述的坐標轉換方法，并結合四階龍格庫塔法求解微分方程[18]，實現將候選路徑上的點從s-q坐標系到笛卡爾坐標系的轉換。

1.3 最優路徑的選擇

在獲取多條候選路徑之后，需要從多條路徑中選出一條最優路徑，使規劃車輛能夠安全、平滑地繞過障礙物。本文提出一種新的代價函數法，通過代價函數的最小化來實現最優路徑的選擇。考慮到駕駛時的安全性和舒服性，本文從安全、平滑和連續這三個方面來設計代價函數，因此，本文提出的代價函數f(i)包含三個部分，如式(4)所示：

f(i)=wsaffsaf(i)+wsmofsmo(i)+wcohfcoh(i)

(4)

其中：i是候選路徑標號,fsaf、fsmo和fcoh分別是安全性代價函數、平滑性代價函數和連貫性代價函數；wsaf、wsmo、wcoh分別是這三個代價函數所占的權重，這三個權重決定車輛的駕駛風格。本文中這3個權值依據經驗分別取0.6、0.2和0.2。

1.3.1 路徑安全性代價函數

安全性是自動駕駛的最重要的因素。障礙物、車道線、道路邊緣是安全性的潛在影響因素。由于任何平面幾何形狀都能被其外接圓包圍，因此本文用外接圓作為描述障礙物的數學模型。

為了避開障礙物和道路邊緣，必須找到并舍棄與障礙物或車道邊緣交叉的候選路徑。本文將圓心到候選路徑的最小距離與圓半徑進行比較來確定該候選路徑是否與障礙物碰撞。圖3(a)給出了一種在單車道上碰撞檢測的示例圖，其碰撞檢測結果用R來表示，候選路徑用ri表示，其中i為序號。如果路徑跨越障礙物或車道邊緣，R=1；否則R=0。

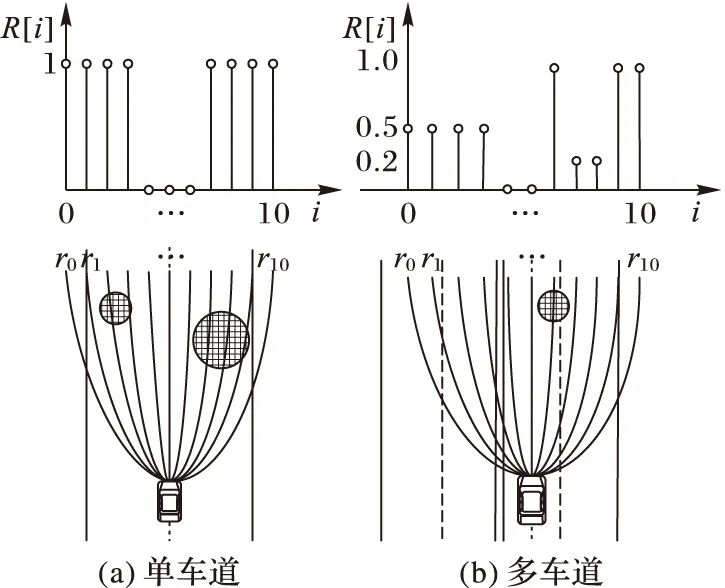
圖3 碰撞檢測結果示意圖

在多車道的碰撞檢測中，本文提出了一種加權碰撞檢測的方法，如圖3(b)所示。如果某候選路徑穿過障礙物或道路邊緣，則R=1；越過對向車道線，則R=0.5；穿過同向車道線，則R=0.2；在本車道上不穿越任何障礙物，則R=0；如果某候選路徑穿過多個種類的車道、道路邊緣或障礙物，則R為它所涉及到的碰撞檢測中的最高值。

如果只考慮碰撞檢測，圖3(a)中r6和圖3(b)中r5都是非碰撞路徑，然而這兩條候選路徑離障礙物的距離太近，如果選擇這兩條路徑，駕駛時稍有不慎車輛就會與障礙物相撞。所以只依靠碰撞檢測來選擇最優路徑無法保證行車的安全性。候選路徑和障礙物之間的距離是評估一條路徑是否安全的有效方法，但是當障礙物或者候選路徑很多時計算量會很大，實時性不高。為了保證安全性和實時性，本文用離散的高斯卷積結合碰撞檢測的方法來定義每條候選路徑的碰撞風險，如式(5)所示：

(5)

其中：fsaf(i)定義為候選路徑ri的安全性代價函數；gi[k]是離散高斯函數，如式(6)所示。

(6)

其中：σ是碰撞風險標準差，決定碰撞檢測的有效范圍，本文實驗中σ=2。

候選路徑的離散高斯卷積過程如圖4(a)、(c)所示。如果i超出候選路徑索引標號的范圍則定義碰撞檢測結果R[i]=1。圖4(b)、(d)分別代表單車道和多車道的碰撞風險值結果。圖4(a)表明r6是一條碰撞檢測最小的路徑，但碰撞風險分布即圖4(b)卻說明r6的風險值不是最低的，即r6不是最安全的路徑，因為它過于接近障礙物。同理，對于多車道，路徑的碰撞風險分布如圖4(d)所示，它說明雖然r5是碰撞檢測最小的路徑，但同時它離障礙物距離過近，最優路徑是r8。

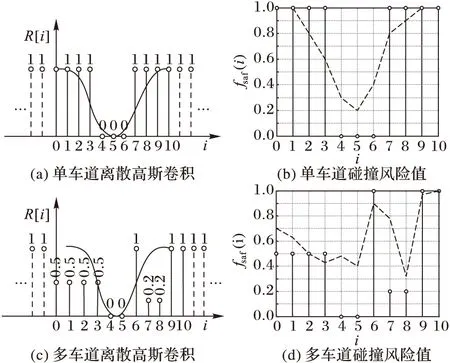
圖4 單車道與多車道碰撞風險示意圖

1.3.2 路徑平滑性代價函數

行駛過程中，不平滑的路徑可能會引起車輪打滑，影響駕駛的安全性和舒適性，因此平滑性也是路徑選擇中必須要考慮的一個因素。由于路徑的平滑性與路徑的曲率直接相關，所以本文利用曲率的平方在路徑上的積分作為平滑性代價函數，如式(7)所示。其中fsmo(i)代表第i條路的平滑性代價函數，Ki(s)是第i條路徑上弧長為s位置的點的曲率，積分的上下限為該候選路徑的弧長s的起點和終點。

(7)

圖5為考慮安全性和平滑性的代價函數曲線圖。圖5(a)是只考慮安全性的代價函數曲線圖，其代價最小值出現在i=10的地方，該路徑的彎度較大，平滑性較差，如圖5(d)中r10所示。圖5(b)是只考慮平滑性的代價函數曲線圖，其代價最小值出現在i=13的地方，該路徑較r10平滑，但是相對遠離車道中心線，如圖5(d)中r13所示。圖5(c)為綜合考慮安全性和平滑性的代價函數曲線圖，其代價最小值為候選路徑r11，如圖5(d)中所示。很明顯，r11相比r10和r13，權衡了安全性和平滑性因素，更合適作為最優路徑。

1.3.3 路徑連貫性代價函數

安全性和平滑性只考慮了本次規劃所涉及到的信息，但是沒有考慮多次規劃的連續性問題，無法保證本次規劃的路徑與上次規劃的路徑沒有出現突變。如果本次規劃路徑與上次規劃路徑的距離太遠，則會出現路徑的突然轉向，不僅影響駕駛的舒適度，嚴重情況下甚至會使車身出現較大的側傾，存在安全隱患。為了解決這個問題，必須考慮上次選擇的最優路徑對本次路徑選擇的影響，因此，本文利用當前候選路徑與上次選擇路徑之間的距離的積分來計算路徑的連貫性代價函數，如式(8)所示：

(8)

其中：s1和s2分別是當前候選路徑與上次選擇路徑在基準線重疊部分的起點和終點；di是本次規劃的第i條候選路徑上的點到上次選擇路徑上相同弧長的點的歐氏距離[19]。

圖6為連貫性代價函數對路徑選擇的影響。圖6(a)和圖6(d)中r6顯示了不考慮連貫性的代價函數和路徑選擇結果，其選擇的路徑偏離了上次規劃的最優路徑rb；圖6(b)是僅考慮連貫性的代價函數；圖6(c)為綜合考慮安全性、平滑性和連貫性的代價函數，其選擇結果如圖6(d)中的r7所示。可以看出，考慮了連貫性的本次規劃的選擇路徑r7相對未考慮連貫性的選擇路徑r6更接近上次規劃的最優路徑rb，因此考慮連貫性因素后，車輛行駛過程中沒有了路徑的突然改變，加強了行駛的安全性和舒適性。

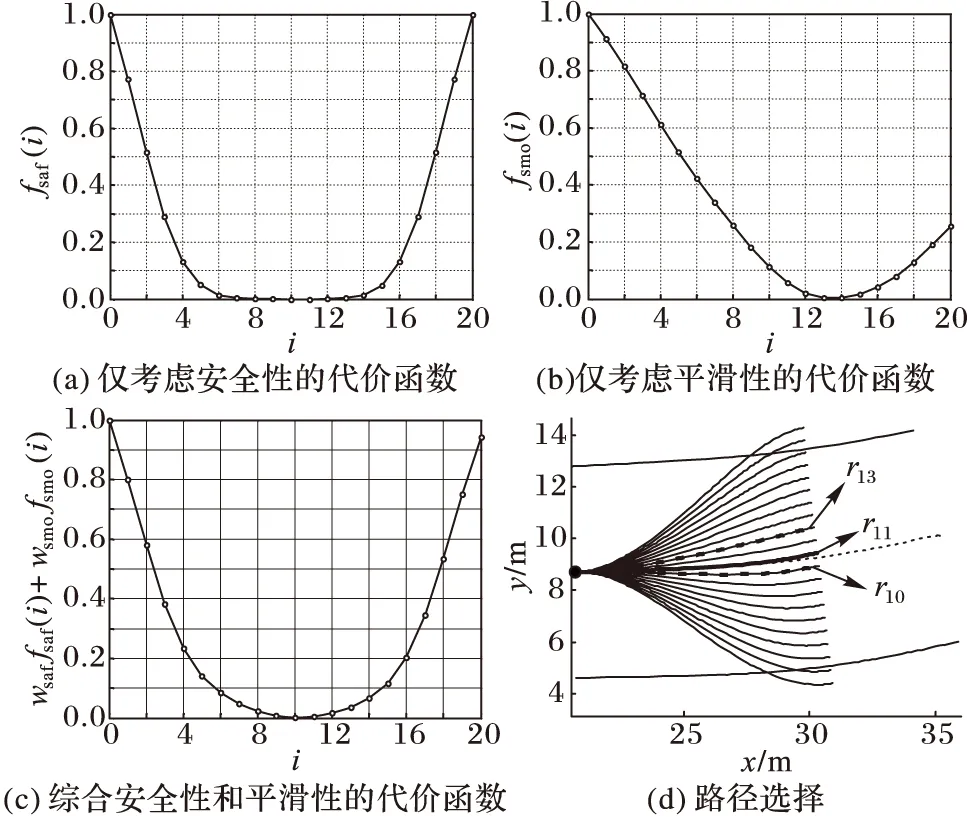
圖5 考慮安全性和平滑性的代價函數和路徑選擇示意圖

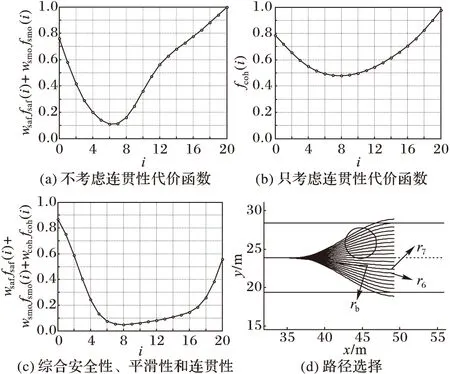
圖6 考慮連貫性的代價函數和路徑選擇示意圖

2 實驗結果和分析

為了驗證本文算法的有效性，本文分別在單車道和多車道上進行避障實驗。本文實驗分為兩部分：第一部分采用多種復雜地形的單車道來驗證算法的性能；第二部分通過模擬與單車道相同路段的多車道，對比測試算法在多車道上的性能。由于實際復雜地形場景地圖較難獲取，因此本文通過Matlab軟件仿真進行實驗，其中地圖數據人工預先定義。圖7和圖8為實驗結果，兩邊黑色實線、黑色長虛線、黑色點虛線和黑色均勻曲線分別表示車道邊界、同方向車道線、基準線以及候選路徑，路中黑色粗實線表示車輛行駛軌跡，空心圓表示障礙物，黑色實心圓表示車輛當前位置。

2.1 復雜地形的單車道避障

有連續多個障礙物的直道、“S”彎道和環島是生活中常見且具有挑戰性的幾種車道類型，即使是人類駕駛員也不能大意，因此本文將這幾類車道作為實驗對象進行測試。

2.1.1 有連續多個障礙物的單車道直道

圖7(a)(d)為本文方法在有連續多個障礙物的直道上測試的結果：圖7(a)為車輛在繞過第一個障礙物的時刻，從圖7(a)中可以看出，車輛選擇了障礙物上邊的一條安全且又平滑的路徑；圖7(d)為車輛通過整段模擬道路的軌跡。從軌跡中可以看出，本文算法能夠規劃出一條有效的路徑，安全地繞過連續多個障礙物并回到基準線上，而且路徑平滑連續，車輛不需要急轉向，滿足駕駛安全和舒適的要求。

2.1.2 有多個障礙物的單車道“S”彎道

圖7(b)(e)為本文方法在“S”彎道路段的測試結果：其中:圖7(b)為規劃車輛在避開第一個彎道上兩個連續障礙物的時刻，車輛選擇了一條居中的較平滑的路徑;圖7(e)為通過包含一個障礙物的第二個彎道的時刻。障礙物在道路正中間，車輛可以選擇從障礙物兩側通過，但是由于平滑性的限制，選擇下方的路徑需要車輛更多的轉向控制，因此本文方法選擇了靠上的路徑作為最優路徑，此路徑安全且平滑。

2.1.3 有多個障礙物的單車道環島路

圖7(c)(f)是車輛在單車道環島路上行駛的實驗結果。圖7(c)表明，當車輛開始進入環狀路時(此時無障礙物)，它沒有選擇車道基準線而是選擇距基準線不遠的偏環狀路內側的路徑作為最優路徑，這是因為靠內側的路徑相比基準線更平滑且足夠安全供車輛行駛；圖7(f)顯示了車輛在環狀路內避開兩個連續障礙物的情況，如圖所示，雖然兩個障礙物相距很近，但是本文的算法可以產生一條平滑且安全的路線使車輛能成功繞過障礙物。

2.2 復雜地形的多車道避障

鄉村和郊區的道路以單車道道路為主，但是城市里和高速上道路主要是多車道道路，因此，本文采用具有與單車道相同路況(障礙物位置相同)的多車道(兩條同向車道和兩條對向車道)來驗證本文方法的有效性。

2.2.1 有連續多個障礙物的多車道直道

圖8(a)(d)為在有多個連續障礙物的多車道直道上的規劃結果。從圖8(a)可以看出，當車輛遇到障礙物時，基于多車道安全性的代價函數規則，會優先選擇當前車道內的最優路徑，但是當前車道有危險時，算法優先選擇了同向車道的一條最優路徑，這與圖7(a)選擇的最優路徑有區別，這是因為應用于多車道的碰撞檢測規則不同；圖8(d)為車輛繞過最后障礙物時刻結果圖，由于障礙物占據了同向兩條車道，所以算法選擇一條跨越對向車道路徑作為最優路徑。當遇到障礙物時，車輛能夠成功避開障礙物。基于平滑性規則，車輛會逐漸回到原車道中，沒有急轉向的突變軌跡。

2.2.2 有多個障礙物的多車道“S”彎道

如圖8(b)(e)為多車道“S”彎道的測試結果，其中圖8(b)與圖7(b)類似，車輛為避開兩個相距很近的障礙物選擇了一條居中的平滑路徑。圖8(e)與圖7(e)顯示了兩種不同的選擇結果，雖然圖8(e)中障礙物上邊的候選路徑有較小的平滑性代價函數，但是如果從上邊避過障礙物，車輛將越過對向車道線。由于對向車道線的代價比同向車道線高，此時總的代價函數是由安全性代價函數主導，所以最終選擇了障礙物下邊的一條安全且平滑的路徑。雖然多車道與單車道規劃結果不同，但是本文的算法都能根據實際情況很好地應用在各種不同車道上。

2.2.3 有多個障礙物的多車道環島路

圖8(c)(f)是本文算法在多車道環島路上的實驗結果。其中圖8(c)結果與7(c)類似，當車輛開始進入環島路時，它選擇了偏環島路內側更平滑的、且屬于當前車道的路徑作為最優路徑；圖8(f)為車輛在多車道環狀路內避開兩個連續障礙物的時刻，可以看出，此次規劃與圖7(f)不同，這是因為在多條候選路徑中，考慮到不同車道線的代價因素，算法優先選擇了同向安全的車道。

由以上對比實驗結果可見，本文方法不管是對于鄉村中單車道道路還是城市中多車道道路，以及各種復雜地形的道路，都能規劃出一條安全、平滑的路徑，有效地避開障礙物。

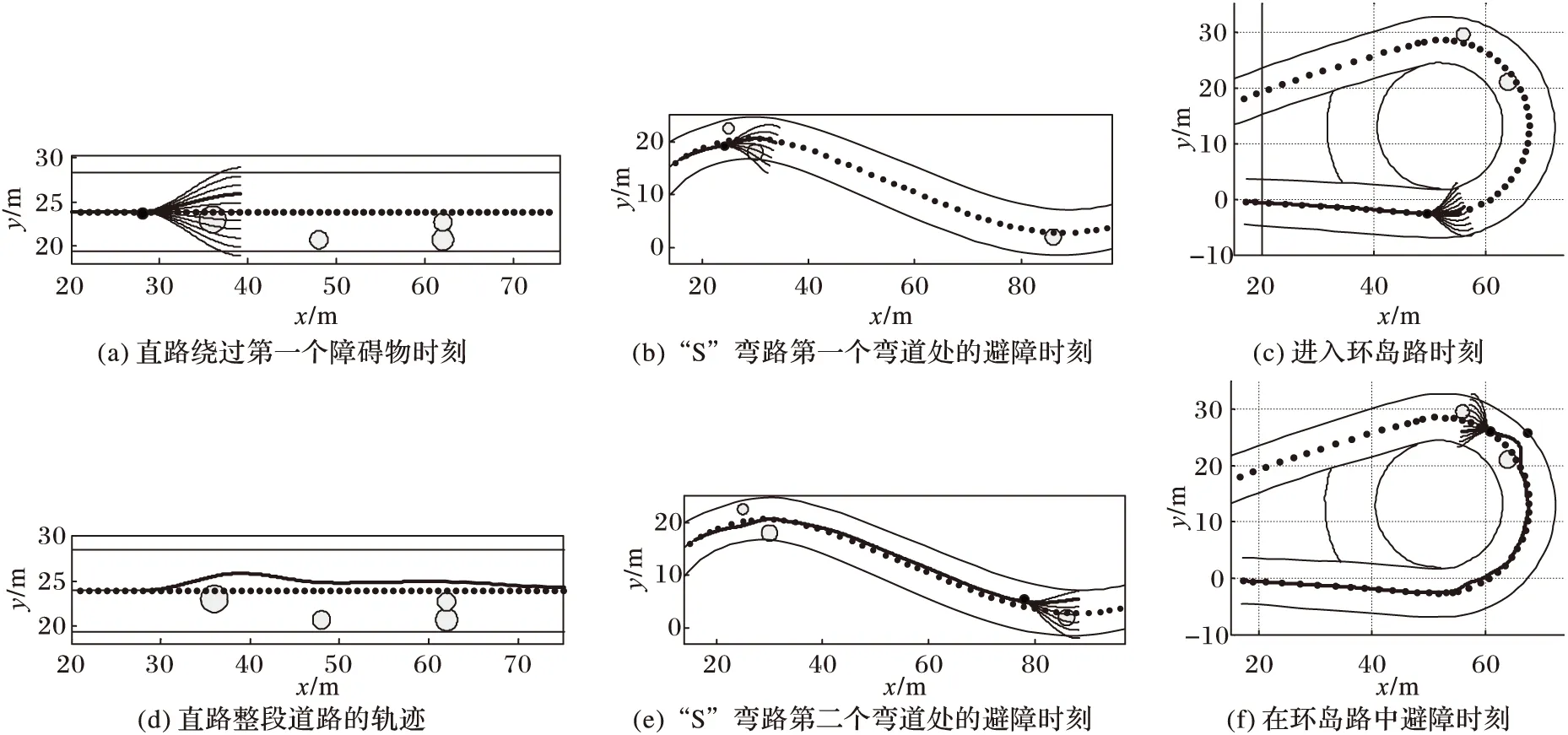
圖7 復雜地形的單車道避障規劃結果

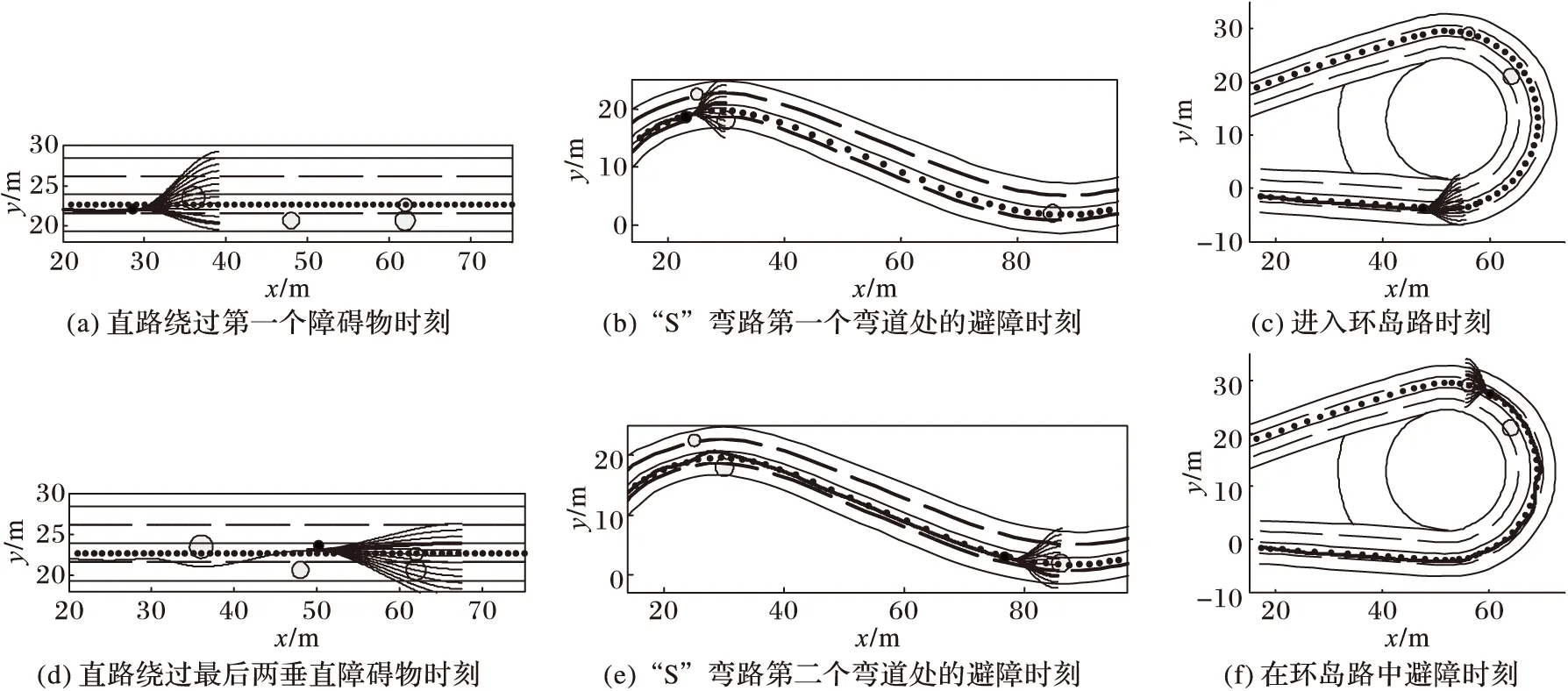
圖8 復雜地形的多車道避障規劃結果

2.3 運行時間

本文實驗硬件平臺為IntelCorei5- 450MCPU(雙核，2.4GHz)，4GB內存；規劃路徑的產生基于VisualStudio2010平臺，道路信息和車輛行駛控制通過Matlab2009b模擬仿真進行。由實驗可知，本文算法在基準線產生和路徑選擇的平均時間分別為3ms和4ms;而路徑產生階段由于要產生多條候選路徑，因此耗時較長，平均時間47ms。所以每次規劃總的平均時間為54ms，即相當于1s內能進行約20次規劃。由于本文設定車輛每行駛1m重新規劃一次，因此本文方法能滿足約20m/s(72km/h)的車輛行駛速度。鑒于車輛在避障時的速度一般低于50km/h，因此本文的方法完全能滿足動態路徑規劃的實時性要求。

3 結語

本文提出了一種新的面向自動駕駛的動態路徑規劃的方法。該方法首先利用地圖信息產生道路基準線，然后依據障礙物的位置和車輛的橫向偏移等信息，在s-q坐標系下產生一簇候選路徑；在路徑選擇階段，本文綜合考慮安全性、平滑性和連續性因素，設計了一種新的代價函數，利用代價函數的最小化來選擇最優路徑。本文在多種復雜地形道路中進行測試，實驗結果表明本文方法不管是對于單車道道路還是多車道道路，都能夠規劃出一條安全、平滑的路徑，引導規劃車輛有效、實時地避開道路中的各個障礙物。

由于本文方法中只考慮了路徑規劃中的靜態障礙物避障問題，并沒有涉及到動態障礙物，因此，未來的工作將集中在動態障礙物的避障問題。

References)

[1] 劉小洋,伍民友.車聯網:物聯網在城市交通網絡中的應用[J].計算機應用,2012,32(4):900-904. (LIU X Y, WU M Y. A vehicular CPS: an application of IoT in vehicular networks [J].Journal of Computer Applications, 2012, 32(4): 900-904.)

[2] 陳榮武,劉莉,諸昌鈐.基于CBTC的列車自動駕駛控制算法[J].計算機應用,2007,27(11):2649-2651. (CHEN R W, LIU L, ZHU C Q. Automatic train operation and its control algorithm based on CBTC [J]. Journal of Computer Applications, 2007, 27(11): 2649-2651.)

[3] 于建志,陳永生.磁浮列車自動駕駛系統控制策略及可靠性研究[J].計算機應用,2010,30(12):3419-3422. (YU J Z, CHEN Y S. Control strategy and reliability study of maglev automatic train operation system [J]. Journal of Computer Applications, 2010, 30(12): 3419-3422.)

[4] GARROTE L, PREMEBIDA C, SILVA M, et al. An RRT-based navigation approach for mobile robots and automated vehicles [C]// INDIN 2014: Proceedings of the 12th IEEE International Conference on Industrial Informatics. Piscataway, NJ: IEEE, 2014:326-331.

[5] 周明秀,程科,汪正霞.動態路徑規劃中的改進蟻群算法[J].計算機科學,2013,40(1):314-316. (ZHOU M X, CHENG K, WANG Z X. Improved ant colony algorithm with planning of dynamic path [J]. Computer Science, 2013, 40(1):314-316.)

[6] 羅元,邵帥,張毅.基于信息融合的移動機器人定位與路徑規劃[J]. 計算機應用,2010,30(11):3091-3093. (LUO Y, SHAO S, ZHANG Y. Location and path planning of mobile robots based on data fusion [J]. Journal of Computer Applications, 2010, 30(11): 3091-3093.)

[7] ZHANG S, DENG W, ZHAO Q, et al. Dynamic trajectory planning for vehicle autonomous driving [C]// SMC ’13: Proceedings of the 2013 IEEE International Conference on Systems, Man, and Cybernetics. Washington, DC: IEEE Computer Society, 2013: 4161-4166.

[8] 王永興,丁睿,姚林泉.移動機器人全局路徑規劃的盲人摸路算法[J].計算機仿真,2010,27(5):157-161. (WANG Y X, DING R, YAO L Q. The blind groping algorithm: global path planning for mobile robot [J]. Computer Simulation, 2010, 27(5): 157-161.)

[9] XU W, PAN J, WEI J, et al. Motion planning under uncertainty for on-road autonomous driving [C]// ICRA 2014: Proceedings of the 2014 IEEE International Conference on Robotics and Automation. Piscataway, NJ: IEEE, 2014: 2507-2512.

[10] KOREN Y, BORENSTEIN J. Potential field methods and their inherent limitations for mobile robot navigation [C]// Proceedings of the 1991 IEEE International Conference on Robotics and Automation. Piscataway, NJ: IEEE, 1991, 2: 1398-1404.

[11] HART P E, NILSSON N J, RAPHAEL B. A formal basis for the heuristic determination of minimum cost paths [J]. IEEE Transactions on Systems Science and Cybernetics, 1968, 4(2):100-107.

[12] STENTZ A. Optimal and efficient path planning for partially known environments [C]// Proceedings of the 1994 IEEE International Conference on Robotics and Automation. Piscataway, NJ: IEEE, 1994: 3310-3317.

[13] WERLING M, ZIEGLER J, KAMMEL S, et al. Optimal trajectory generation for dynamic street scenarios in a Frenét frame [C]// ICRA 2010: Proceedings of the IEEE International Conference on Robotics and Automation. Piscataway, NJ: IEEE, 2010:987-993.

[14] CHU K, LEE M, SUNWOO M. Local path planning for off-road autonomous driving with avoidance of static obstacles [J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(4): 1599-1616.

[15] BAGIROV A M. Numerical methods for minimizing quasidifferentiable functions: a survey and comparison [M]// Quasidifferentiability and Related Topics. Berlin: Springer-Verlag, 2000: 33-71.

[16] SANDE H V, HENROTTE F, HAMEYER K. The Newton-Raphson method for solving non-linear and anisotropic time-harmonic problems [J]. COMPEL: The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2004, 23(4): 950-958.

[18] FAMELIS I Th, TSITOURAS Ch. On modifications of Runge-Kutta-Nystr?m methods for solvingy(4)=f(x,y) [J]. Applied Mathematics and Computation, 2016, 273: 726-734.

[19] HUANG H-X, LIANG Z-A, PARDALOS P M. Some properties for the Euclidean distance matrix and positive semidefinite matrix completion problems [J]. Journal of Global Optimization, 2002, 25(1): 3-21.

This work is partially supported by the National Natural Science Foundation of China (41401525), the Natural Science Foundation of Guangdong Province (2014A030313209), the Student’s Platform for Innovation and Entrepreneurship Training Program of Hubei Province (201410512030).

ZHOU Huizi, born in 1995. Her research interests include dynamic path planning.

HU Xuemin, born in 1985, Ph. D., lecturer. His research interests include computer vision, dynamic path planning.

CHEN Long, born in 1985, Ph. D., lecturer. His research interests include stereo vision, autonomous driving.

TIAN Mei, born in 1995. Her research interests include dynamic path planning.

XIONG Dou, born in 1995. Her research interests include automatic control.

Dynamic path planning for autonomous driving with avoidance of obstacles

ZHOU Huizi1, HU Xuemin1*, CHEN Long2, TIAN Mei1, XIONG Dou1

(1.SchoolofComputerScienceandInformationEngineering,HubeiUniversity,WuhanHubei430062,China; 2.SchoolofDataandComputerScience,SunYat-senUniversity,GuangzhouGuangdong510006,China)

To deal with the problem of dynamic path planning for autonomous driving with avoidance of obstacles, a real-time dynamic path planning approach was proposed to avoid obstacles in real-time under the condition of knowing initial vehicle position, speed, orientation and the obstacle positions. Firstly, a base frame of the road was constructed using the continuity of the second derivative for cubic spline curves combined with the information of the road edges and lanes. Secondly, thes-qcoordinate system was established using the position and orientation of the vehicle and the curvature of the road. Then a set of smooth curves from the current position to the destination were generated as the path candidates in thes-qcoordinate system. Finally, considering the factors of safety, smoothness and continuity, a novel cost function was designed, and the optimal path was selected by minimizing the cost function. Various simulative roads were designed to test the proposed method in the experiments. The experimental results show that the proposed approach has the ability of planning a safe and smooth path for avoiding the obstacles on both single-lane roads and multi-lane roads with good real-time performance.

autonomous driving; dynamic path planning; path candidate; path selection; cost function

2016- 07- 18;

2016- 08- 22。

國家自然科學基金青年基金資助項目(41401525)；廣東省自然科學基金資助項目(2014A030313209)；湖北省大學生創新創業訓練計劃基金資助項目(201410512030)。

周慧子(1995—)，女，遼寧沈陽人，主要研究方向：動態路徑規劃； 胡學敏(1985—)，男，湖南岳陽人，講師，博士，主要研究方向：計算機視覺、動態路徑規劃； 陳龍(1985—)，男，湖北襄陽人，講師，博士，主要研究方向：立體視覺、無人駕駛； 田梅(1995—)，女，湖北武漢人，主要研究方向：動態路徑規劃； 熊豆(1995—)，女，湖北武漢人，主要研究方向：自動控制。

1001- 9081(2017)03- 0883- 06

10.11772/j.issn.1001- 9081.2017.03.883

TP391.7

A