阻抗式調壓室波動穩定分析的方法探究

馮熊

（蘭州資源環境職業技術學院蘭州730020）

阻抗式調壓室波動穩定分析的方法探究

馮熊

（蘭州資源環境職業技術學院蘭州730020）

文章通過對阻抗式調壓室波動穩定分析方法的探討，分別采用解析法、圖解法、電算法進行最高涌浪和最低涌浪求解，對三種方法的計算結果進行了分析對比，簡述了三種方法在調壓室波動穩定分析時的優缺點。本文為蘭州資源環境職業技術學院2016年校級科研項目引水式水電站引水系統水錘壓強及調壓室波動穩定分析研究項目成果。

調壓室；解析法；圖解法；電算法

1 引言

引水式水電站調壓室的常見形式有圓筒式、阻抗式、差動式、氣墊式等多種，在進行調壓室斷面尺寸設計的過程中，必須進行波動穩定分析，以確定其最高涌浪及最低涌浪，在進行穩定分析時，可通過解析法、圖解法、電算法多種方法進行比較計算，最終確定調壓室的尺寸。

某引水式水電站的總裝機容量為7.2萬kw、水庫的總庫容1.47億m3，最大處壩高100m。水庫的正常蓄水位為512.0m，水庫的設計洪水位為511.1m，校核洪水位為512.5m，水庫的死水位為485.0m。水電站的下游尾水位，當最大引用流量為Q=93m3/s時，下游尾水位為408.8m，當引用流量為Q=31m3/s時，下游正常尾水位為408.5m，當半臺機組運行時，下游最低尾水位408.18m，設計洪水位引用流量Q=3040m3/s時，下游尾水位為414.10m，校核洪水位引用流量Q=3290m3/s時，下游尾水位414.40m。

2 解析法

2.1 最高涌浪

在計算最高涌波水位時，上游水庫應取正常高水位，引水道的糙率應取可能的最小值，負荷的變化情況一般按丟棄全負荷設計。最高洪水位丟棄全負荷或部分負荷進行校核。在水電站工程中，根據給出的工程資料，上游正常高水位Z正=512m，引水道的糙率取n=0.013進行計算。

計算步驟如下：（1）準備基本數據：引水道長L（m），斷面積f(m2),機組滿發時的恒定流速v0(m/s)，調壓室斷面積F(m2)，恒定流情況下的水頭損失hw0(m)；（2）計算參數；（3）將水頭、涌浪…均除以S，化為無因次量，如恒定流水頭損失hw0化為X0=hw0/S，最高涌浪Zm化為Xm=Zm/S等等；（4）計算求出X0，進行試算求出Xm；（5）試算求出Xm后，再進行試算求出X2。

現分別選取D=12m、14m、16m、18m進行最高涌浪計算。

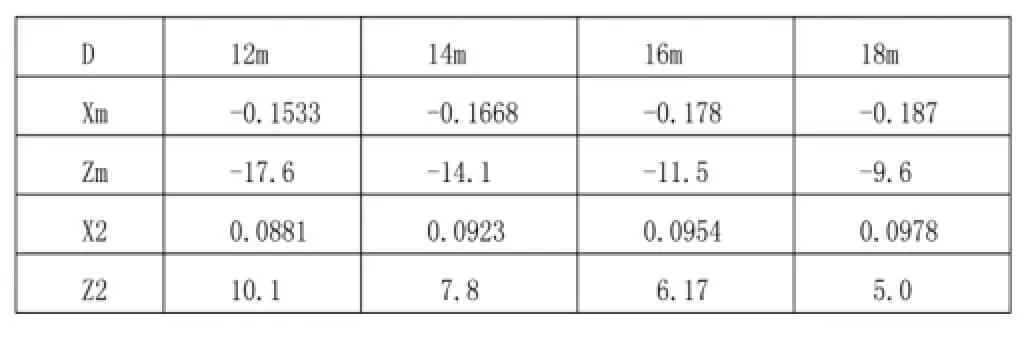
表1 3臺—0甩負荷時最高涌浪

2.2 最低涌浪

在水電站的最低涌波水位的計算過程中，根據工程資料，上游水位取最低水位，引水道的糙率取可能的最大糙率。

因為在死水位時，有可能引用流量達不到最大值，所以，在計算此水電站最低涌波水位時，按負荷由0突增到Q/3時的增荷條件進行計算。即由0增加到31m3/S。

表2 突增負荷0-Q0/3時最低涌浪

3 圖解法

圖解法是用作圖的方法來積分波動微分方程式，其實質是用有限差的比值和，然后逐時段地求解，最后得出水位、流速和時間的關系。連續方程和動力方程可改寫為ΔZ=A-αV、ΔV=β(Z-hw)。式中A=Δt，α=Δt，β=Δt。當計算時段選定后，A、α、β均為常數。計算的基本假定是：在時段Δt的過程中調壓室的水位Z和引水道的流速V保持不變，而集中在時段的末尾，即假定Z和V的變化是“階梯式”的，這是圖解法的近似之處，一般說來，Δt取得越小，結果越精確，但Δt太小，不僅加大計算工作量，而且會因圖解不便而使誤差增大，通常希望從開始作圖經1過8～10個Δt后，水位達到最大值，因此，可取Δt=～，T為波動的周期，按下公式計算T=2π。

3.1 全棄負荷時最高涌浪

在水電站引用流量由3臺機組變為0時，調壓室水位即開始上升，流速會因調壓室水位上升變小，但但因計算時段Δt非常小，所以假定在Δt時段中流速仍為Vmax，因此在第一時段內，調壓室水位的升高值ΔZ1=ΔtV，即等于直線ΔZ=f(V)上與Vmax相對應點的縱max坐標。從點Ⅰ向上量取ΔZ1得Z1，此點即為第一時段Δt（1即第二時段Δt2初）末的調壓室水位。

第一時段Δt1末引水道的流速變化ΔV1=β(Z-hw1)，其中hw1≈hw0，Z1-hw1=ΔZ1。ΔV1可以直接從圖解法求出。從點Ⅰ作直線平行于直線ΔV=β(Z-hw1)，與經過Z1點的水平線交于點Ⅱ，線段Z1Ⅱ的長度即等于ΔV1，Ⅱ點的橫坐標為Δt1末（Δt2初）引水道的流速。用同樣的方法可求出Ⅱ、Ⅲ、Ⅳ、Ⅴ……。連接Ⅰ、Ⅱ、Ⅲ、Ⅳ……即得調壓室的Z～V曲線，得出調壓室的最高涌浪Zmax= 14.6m，如圖1所示。

3.2 增加負荷時最低涌浪

增加負荷時，水輪機的引用始流量由0增加為31m3。在起始時刻，調壓室水位在點Ⅰ，Δt1時間內調壓室水位降低ΔZ1，可以從ΔZ1=f(V)線上量取。求ΔV時，平行ΔV=β(Z-∑h)的斜線需從∑h曲線上的Ⅰ'、Ⅱ'、Ⅲ'、……開始作起，圖中經過Ⅰ、Ⅱ、Ⅲ、……曲線表示調壓室的水位變化。連接Ⅰ、Ⅱ、Ⅲ、……即得調壓室水位變化曲線，得出調壓室的最低涌浪Zmin=7.3m，如圖2所示。

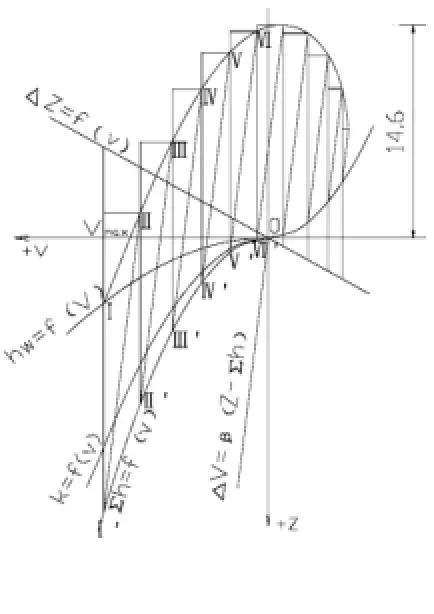
圖1 丟棄全部負荷時的圖解分析

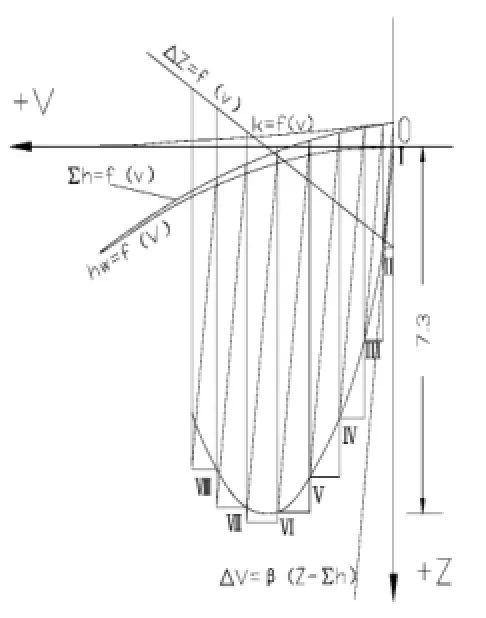
圖2 增加負荷時的圖解分析

4 電算法

隨著電子計算機的廣泛運用，在調壓室波動分析過程中，通過編制程序進行計算可快速得出結果，而且可計算不同條件下的最高涌浪及最低涌浪，具有計算速度快，結果精度高，使用范圍廣等優點。下面分別給出在校核洪水位條件下，丟棄全負荷時，不同調壓室尺寸的波動圖形。

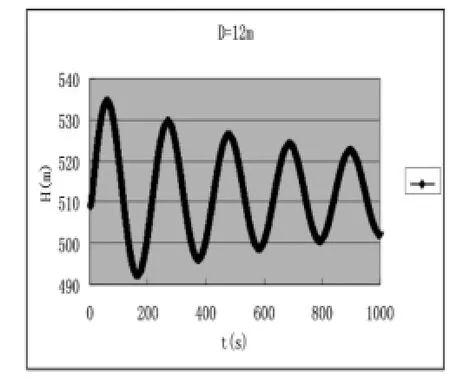
圖3 D=12m時，3臺—0甩負荷

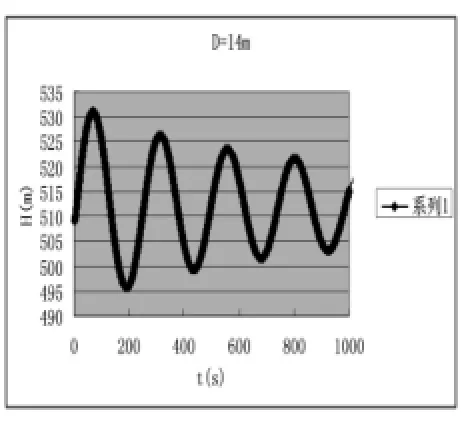
圖4 D=14m時，3臺—0甩負荷

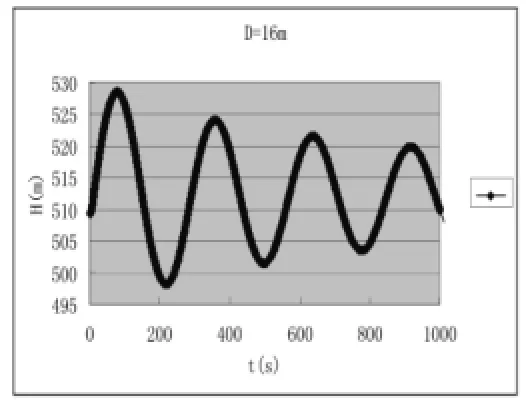
圖5 D=16m時，3臺—0甩負荷

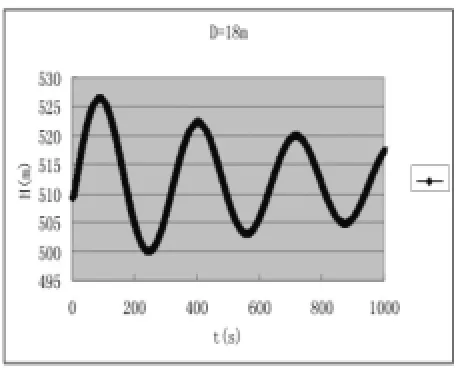
圖6 D=18m時，3臺—0甩負荷

5 結果分析

在前面的分析中，我們用到了解析法、圖解法、電算法三種方法。分別用這三種方法計算了調壓室的涌浪。用解析法進行波動計算，僅能分析調壓室波動過程的一些特殊情況，且只能得到最后結果，無法得知波動過程，但解析法計算較簡便；用圖解法計算調壓室的涌浪，不但可以求出最高和最低涌浪，還能清楚地看到波動變化過程；電算法與解析法和圖解法相比，計算理論嚴密，簡化假設少，速度快，精度高，可以計算不同類型調壓室在各種工況下的涌浪全過程并可與水錘、機組和轉速變化聯合求解。因此，在本工程中，采用圖解結果進行設計調壓室的尺寸，可用電算法和解析法的計算結果來檢驗。

[1]金錐、姜乃昌、汪興華、關興旺編著.停泵水錘及其防護[M].第二版.北京：中國建筑工業出版社，2004

[2]湖南省水力發電工程學會.湖南省電力公司編.水電站事故[M].北京：中國電力出版社，2004[3]陳乃祥主編.水利水電工程的水力瞬變仿真與控制[M].北京：中國水利水電出版社，2005

[4]西安理工大學水利水電學院.嵐河藺河口水電站壓力引水系統水力學模型試驗報告[R]西安：西安理工大學，2000

[5]王樹人.調壓室計算理論及方法[M].北京：清華大學出版社，1986

馮熊（出生年月1985年10月——），性別：女籍貫：重慶萬州，民族：漢，學位：學士，職稱：講師，研究方向：水利水電工程，單位院系：蘭州資源環境職業技術學院水電工程系。