基于Duhamel積分的地震作用下車橋耦合振動(dòng)分析
謝智奕, 沈火明
(西南交通大學(xué)力學(xué)與工程學(xué)院,四川成都 610031)
?
基于Duhamel積分的地震作用下車橋耦合振動(dòng)分析
謝智奕, 沈火明
(西南交通大學(xué)力學(xué)與工程學(xué)院,四川成都 610031)
文章應(yīng)用達(dá)朗貝爾原理推導(dǎo)了6自由度車輛模型,應(yīng)用有限元法推導(dǎo)了橋梁模型,應(yīng)用逆迭代法求解兩個(gè)系統(tǒng)的模態(tài)振型和自振頻率,采用加速度輸入模式將地震輸入到車橋耦合系統(tǒng)中,最后通過(guò)Duhamel積分法和振型疊加法求得車橋耦合系統(tǒng)的動(dòng)力響應(yīng),通過(guò)算例與傳統(tǒng)Newmark-β法相對(duì)比,結(jié)果表明:通過(guò)本文方法計(jì)算的地震作用下車橋耦合的動(dòng)力響應(yīng)結(jié)果與傳統(tǒng)Newmark-β法的結(jié)果接近,極值點(diǎn)誤差范圍在5 %以內(nèi)。
車橋耦合; 地震作用; Duhamel積分; Newmark-β法; 振型疊加法
隨著高速鐵路的大量普及,客運(yùn)列車向著高速化、貨運(yùn)列車向著重載化的方向發(fā)展,車橋耦合問(wèn)題已經(jīng)成為國(guó)內(nèi)外學(xué)者研究的熱點(diǎn)[1-6]。而地震作用會(huì)對(duì)橋梁造成嚴(yán)重破壞,極大地影響橋梁上車輛行駛的安全,因此對(duì)地震作用下的車橋耦合問(wèn)題研究具有重要意義。地震波在地面的運(yùn)動(dòng)是一種復(fù)雜的空間運(yùn)動(dòng),地震加速度不僅包括水平向分量,還包括豎向分量。根據(jù)大量資料及研究[1-5]、[10],雖然水平作用對(duì)橋梁結(jié)構(gòu)的影響最大,但是當(dāng)車輛行駛在橋梁上時(shí),地震的豎向作用對(duì)車輛行駛危害也非常大,甚至?xí)斐擅撥壩kU(xiǎn),極大地威脅著車輛及乘客的安全,所以本文主要研究地震的豎向作用。目前研究地震作用下的車橋耦合問(wèn)題通常采用的是Newmark積分法等逐步積分法,但是該方法對(duì)時(shí)間精度的要求較高,而一些地震波的記錄由于持時(shí)較長(zhǎng),所取時(shí)間間隔也相對(duì)較長(zhǎng),這就影響了計(jì)算的精確度。本文采用基于Duhamel積分的車橋耦合動(dòng)力分析方法,該方法能顯著提高積分步長(zhǎng)[6],從而解決了地震波記錄數(shù)據(jù)時(shí)間間隔的問(wèn)題。
1 Duhamel積分法[6]
設(shè)一低阻尼單自由度系統(tǒng)的運(yùn)動(dòng)方程為
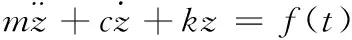
(1)
其中m、k、c是系統(tǒng)的質(zhì)量、剛度和阻尼,z為位移,f(t)為荷載力。整理得到:
(2)

將式(2)的解用Duhamel積分展開(kāi)并整理得到:
(3)
求導(dǎo)得到:
(4)
式中:
(5)
(6)
(7)
(8)
(9)
這里假設(shè)荷載在(t, t+Δt)內(nèi)是線性變化的,有
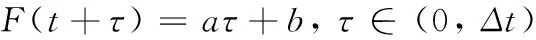
(10)
通過(guò)式(10)可以確定參數(shù)a,b的值。對(duì)于某確定結(jié)構(gòu),其ω、ξ為定值,在Δt不變的情況下,計(jì)算中的H、Q和P也保持不變,根據(jù)式(3)和式(4)將上一時(shí)刻的動(dòng)力響應(yīng)帶入計(jì)算可得下一時(shí)刻的動(dòng)力響應(yīng),在整個(gè)時(shí)間段內(nèi)依次積分最后得全時(shí)間段的動(dòng)力響應(yīng)。
2 車橋耦合模型
2.1 橋梁模型
橋梁系統(tǒng)包括主梁、橋墩和支座,本文在計(jì)算時(shí)不考慮支座和墩高對(duì)車橋耦合的影響,故設(shè)橋墩與主梁剛結(jié),橋墩與主梁參數(shù)一致。采用平面剛架單元建立橋梁有限元模型,其位移向量為[ui,vi,θi,uj,vj,θj]T,單元內(nèi)部點(diǎn)的位移計(jì)算采用Hermite插值[7]計(jì)算,質(zhì)量矩陣采用一致質(zhì)量矩陣,其單位質(zhì)量矩陣為:
(11)
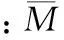
橋梁阻尼采用Rayleigh阻尼,
CB=a0MB+a1KB
(12)
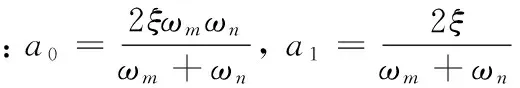
ωm、ωn為橋梁系統(tǒng)前兩階自振頻率,MB、KB分別為橋梁的質(zhì)量矩陣和剛度矩陣。
2.2 車輛模型
車輛系統(tǒng)采用剛體-彈簧-阻尼的整車模型,由于沿車輛運(yùn)行方向的縱向振動(dòng)對(duì)橋梁的豎向振動(dòng)影響極小,并且車輛豎向與橫向振動(dòng)之間的耦合效應(yīng)較弱,因此本文在計(jì)算時(shí)將車橋耦合振動(dòng)響應(yīng)分為豎向與橫向兩個(gè)平面振動(dòng),所以在車橋耦合振動(dòng)分析中,僅分析車輛的浮沉與點(diǎn)頭2個(gè)自由度,包括車體及前后轉(zhuǎn)向架共6個(gè)自由度。假設(shè)兩轉(zhuǎn)向架的一、二系彈簧剛度、阻尼系數(shù)相同,采用達(dá)朗貝爾原理推導(dǎo)其質(zhì)量矩陣、剛度矩陣和阻尼矩陣,得到車輛系統(tǒng)的運(yùn)動(dòng)方程[1]。
2.3 車橋耦合模型
橋梁與車輛系統(tǒng)的運(yùn)動(dòng)方程為:
(13)
(14)
式中下標(biāo)B、V分別代表橋梁系統(tǒng)和車輛系統(tǒng),F(xiàn)BV和FVB為車輛與橋梁的相互作用力。
兩個(gè)系統(tǒng)通過(guò)輪軌接觸相聯(lián)系,本文不考慮軌道不平順的影響,對(duì)兩個(gè)系統(tǒng)采用振型疊加法,將其運(yùn)動(dòng)方程化為模態(tài)運(yùn)動(dòng)方程[6]。
對(duì)于橋梁系統(tǒng),設(shè)其為正交阻尼結(jié)構(gòu),采用逆迭代法求解系統(tǒng)的振型ΦB和自振頻率ωB,假設(shè)各階模態(tài)阻尼比為ξB,設(shè)橋梁的廣義振型坐標(biāo)列向量為qB,則位移向量可表示為:
(15)
將式(15)代入式(13)中,可以得到橋梁系統(tǒng)的模態(tài)運(yùn)動(dòng)方程:
(16)
對(duì)于車輛系統(tǒng),由于其阻尼矩陣CV不具有正交性,因此引入假定的車輛阻尼比ξV,并將式(14)中的阻尼相移動(dòng)到右端,再進(jìn)行同樣的模態(tài)變換,可以得到車輛系統(tǒng)的模態(tài)運(yùn)動(dòng)方程:
(17)
3 地震激勵(lì)的輸入
地震激勵(lì)的輸入采用加速度輸入模式[8],直接運(yùn)用實(shí)測(cè)地震波的加速度時(shí)程,不考慮行波效應(yīng),廣義地震力[5]為:
(18)
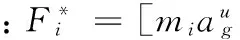
4 算例
選取單節(jié)四軸列車在地震作用下通過(guò)一32 m的簡(jiǎn)支梁橋作為算例,地震波選取典型強(qiáng)震記錄El-Centro波輸入,采用縱向+豎向一致輸入,豎向地震加速度時(shí)程與縱向一致,但加速度峰值取0.65倍。不考慮軌道不平順,車速v取50 m/s,車輛信息見(jiàn)文獻(xiàn)[9]。橋梁彈性模量E取35 GPa,橫截面積A為4.8 m2,截面抗彎慣性矩I取22 m4,密度取2 600 kg/ m3,橋梁劃分為長(zhǎng)度一致的320個(gè)梁?jiǎn)卧∏?0階模態(tài),各階模態(tài)阻尼比取為0.05。當(dāng)?shù)卣痖_(kāi)始時(shí)列車上橋,地震持時(shí)50 s,步長(zhǎng)取與地震波記錄時(shí)間間隔一致為0.02 s。為驗(yàn)證本方法的正確性,將本文方法與傳統(tǒng)Newmark-β法的結(jié)果作對(duì)比,計(jì)算結(jié)果如圖1和圖2所示。
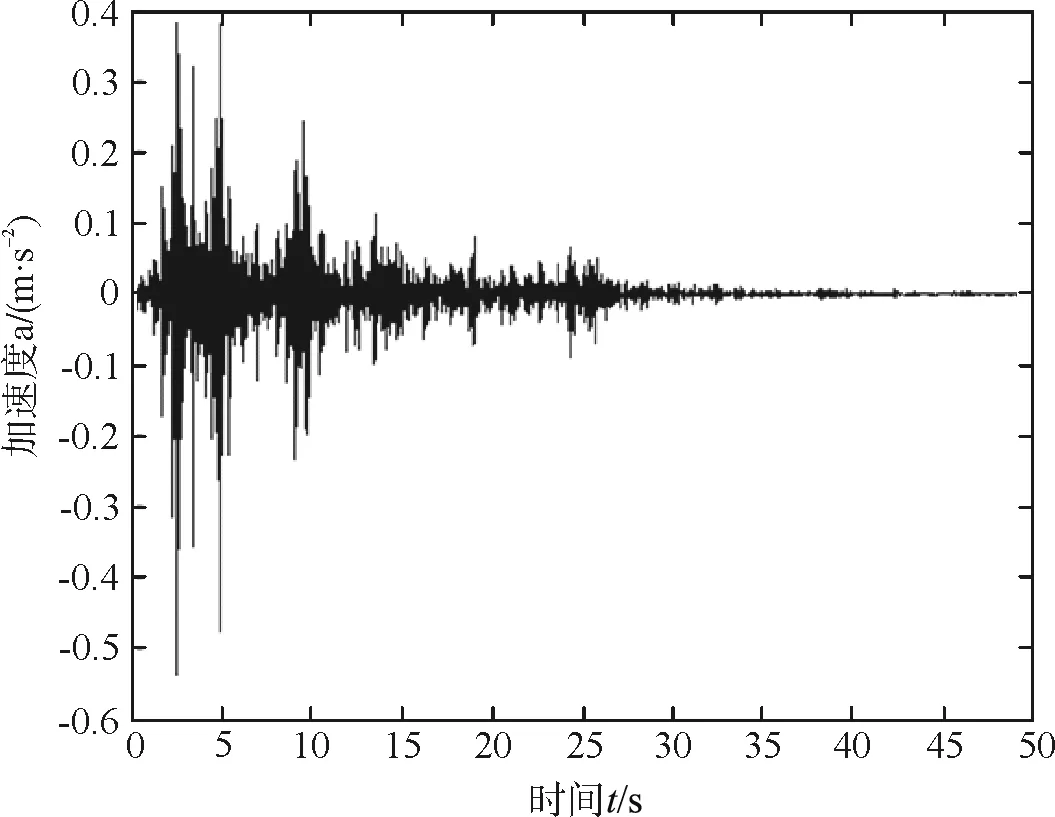
圖1 Newmark-β法計(jì)算的橋梁跨中豎向加速度時(shí)程
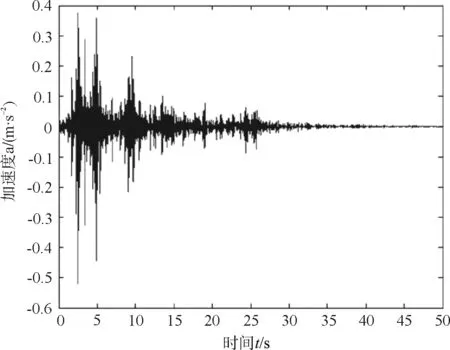
圖2 本文方法計(jì)算的跨中加速度時(shí)程
從圖1和圖2可見(jiàn),本文的方法和傳統(tǒng)Newmark-β法求得的地震作用下車橋耦合動(dòng)力響應(yīng)結(jié)果非常接近,極值點(diǎn)的誤差范圍在5 %以內(nèi),說(shuō)明本文的方法可行。
5 結(jié)束語(yǔ)
應(yīng)用達(dá)朗貝爾原理推導(dǎo)了6自由度車輛模型,應(yīng)用有限元法推導(dǎo)了橋梁模型,應(yīng)用逆迭代法求解兩個(gè)系統(tǒng)的模態(tài)振型和自振頻率,采用加速度輸入模式將地震輸入到車橋耦合系統(tǒng)中,最后通過(guò)Duhamel積分法和振型疊加法求得車橋耦合系統(tǒng)的動(dòng)力響應(yīng),并與傳統(tǒng)Newmark-β法相對(duì)比,驗(yàn)證了本文方法的可行性。
[1] XIA H,DEROECKG,GOICOLEAJ M.Bridgevibration and controls: newresearch [M].New York:Nova Science Publishers Inc.,2011:15 -65.
[2] 翟婉明.車輛-軌道耦合動(dòng)力學(xué)[M]. 北京:科學(xué)出版社,2007:1-11,116-133.
[3] 翟婉明,夏禾. 列車-軌道-橋梁動(dòng)力相互作用理論與工程應(yīng)用[M]. 北京:科學(xué)出版社,2011 : 8-23.
[4] 杜憲亭. 強(qiáng)地震作用下大跨度橋梁空間動(dòng)力效應(yīng)及列車運(yùn)行安全研究[D]. 北京:北京交通大學(xué),2011.
[5] 夏禾. 車輛與結(jié)構(gòu)動(dòng)力相互作用[M]. 北京:科學(xué)出版社,2002 : 11 -29,88 -92,200-207.
[6] 喬宏,夏禾,杜憲亭. 基于Duhamel積分的車橋耦合動(dòng)力分析方法[J]. 西南交通大學(xué)學(xué)報(bào),2014,49(5): 766-771.
[7] 余華,吳定俊. Hermite插值在車橋禍合振動(dòng)中的應(yīng)用[J]. 振動(dòng)與沖擊, 2006,25(2): 38-40.
[8] 董延龍. 地震作用下高鐵的車橋耦合振動(dòng)分析[D]. 武漢: 華中科技大學(xué),2013: 16-18.
[9] 杜憲亭,夏禾,張?zhí)铮? 基于精細(xì)Runge-Kutta混合積分法的車橋耦合振動(dòng)非迭代求解算法[J]. 振動(dòng)與沖擊,2013,32(13): 39-42.
[10] 賈志明,高大峰. 基于大質(zhì)量法地震豎向作用下連續(xù)剛構(gòu)橋地震響應(yīng)分析[J]. 四川建筑, 2011,31(1): 140-141.
謝智奕(1991~),男,碩士研究生,研究方向?yàn)樵肼暸c振動(dòng)控制。
沈火明(1968~),男,博士,教授,博士生導(dǎo)師,研究方向?yàn)榻Y(jié)構(gòu)振動(dòng)與控制。
U441+.3
A
[定稿日期]2017-03-25

