貝類養殖吊籠水動力特性的實驗研究

趙云鵬廖 鵬畢春偉李明智

（1大連理工大學，海岸和近海工程國家重點實驗室，遼寧大連116024；2大連海洋大學航海與船舶工程學院，遼寧大連116023）

貝類養殖吊籠水動力特性的實驗研究

趙云鵬1，廖 鵬1，畢春偉1，李明智2

（1大連理工大學，海岸和近海工程國家重點實驗室，遼寧大連116024；2大連海洋大學航海與船舶工程學院，遼寧大連116023）

通過模型實驗的方法分別探討了規則波和均勻流作用下貝類養殖吊籠的水動力特性，并分析了貝類養殖密度對吊籠受力的影響。在波浪作用下，基于莫里森方程，通過最小二乘法計算水動力系數Cd和慣性力系數Cm值；在水流作用下，利用簡化莫里森公式反推出Cd值；分析了Kc數、雷諾數Re和養殖密度對Cd和Cm的影響。結果顯示：吊籠的運動幅度及受力隨著波高、周期及流速的增大而增大；隨著貝類養殖密度的增大，吊籠受到的水平力逐漸增大，而吊籠的運動幅度逐漸減小；在波浪效應下，隨著Kc數、Re的增大，Cd有略微增大趨勢，而Cm則先增大后趨于常數；在水流作用下，Cd值隨著雷諾數Re的增大無顯著變化；在同一工況下，Cd隨著貝類養殖密度的增加而增大，而Cm相應減小。研究表明，本實驗得出的吊籠水動力系數可作為計算吊籠波浪力和流阻力時的取值參考。

吊籠；水動力系數；規則波；均勻流；養殖密度

筏式吊籠養殖是貝類海水工業化養殖普遍采取的形式［1－3］。吊籠系統受力計算是浮筏養殖結構設計及優化的關鍵所在。由于吊籠直徑遠小于海浪波長，故工程上一般用Morison方程［4］對其進行受力分析。而運用Morison方程的關鍵在于水動力系數的選取。中國港口規范［5］對于實體圓柱給出經驗取值，速度力系數Cd為1.2和慣性力系數Cm為2.0。吊籠為透空圓柱體結構，主要由圓柱形網衣和分層網片構成，在波浪和水流下網衣是主要受力構件。

近年來國內外學者圍繞網衣的水動力特性開展了諸多研究，如：傅恩波等［6］通過實驗測量了作用在平面網衣上的波浪力，得出波浪下的拖曳力系數與水流中的近似；趙云鵬等［7］通過網衣波浪實驗分析了雷諾數與拖曳力系數和慣性力系數的關系；劉莉莉等［8］對單片網在振蕩流中的水動力系數進行實驗探究，給出了水動力系數隨Kc數、雷諾數Re的變化規律；日本學者田內等給出的網片與水流垂直時受力計算經驗公式中，速度力系數Cd為1.76［9］；蘇聯學者巴拉諾夫等建議Cd取1.5，而列維恩等認為Cd取 2.16［9］；Balash等［10］認為Cd隨著雷諾數增大趨于穩定，網衣密實度是影響Cd的重要因素。但上述結論的研究對象僅是單片網衣，與吊籠的圓型網衣有所區別。詹杰民等［11］對平面網衣和圓型網衣的阻力進行比較分析，認為同樣網面積下圓型網衣阻力較小。迄今關于養殖貝類水動力特性的研究不多。

中國臺灣學者李冠穎［12］對水流下牡蠣的流阻力系數進行實驗測量，得出其平均值為1.83；Plew［13］做了貽貝串在水流下的生物泵效應實驗，認為貽貝的進食活動對貽貝串的速度力系數影響不大，貽貝串的Cd大致為1.3。再具體到吊籠及其中貝類養殖密度對水動力特性綜合影響這方面研究還比較少。

基于上述分析，本文在小波流水槽開展規則波、均勻流及貝類養殖密度對吊籠模型水動力特性影響的實驗研究，給出水動力系數與養殖密度、Kc數、雷諾數Re的關系，為吊籠水動力系數的取值提供參考。

1 材料與方法

1.1 試驗材料

1.1.1 吊籠模型

在亞洲，采用吊籠養殖扇貝是一項很成熟的技術。貝類，吊籠模型及原型圖如圖1所示。

圖1 貝類，吊籠模型及原型圖Fig.1 Shellfish，lantern net model and its prototype

中國水產養殖領域普遍采用的吊籠有5層、10層、15層等不同類型。本研究參照5層原型吊籠，按照克列斯登生漁具模型試驗準則［14］設計模型，模型與原型比例1∶2，吊籠模型底盤直徑15 cm，層高5 cm，網衣和分層網片采用聚乙烯材質，目腳長0.5 cm，網線直徑0.1 cm。

1.1.2 貝殼模型

貝殼模型選用已剝蜆殼內包橡皮泥，外口用膠槍融射膠棒密封，模型平均直徑2 cm，換成原型直徑4 cm。美國糧農研究中心［15－16］給出貝類吊籠養殖規范建議，當貝苗直徑大于2.8 cm時，最優放養密度為800個／m2。中國水產養殖為保障存活率建議籠養扇貝3 cm苗放養密度為565～778個／m2。

在本實驗中，每層每次投放貝殼模型兩枚，分5次投放，直到每層10枚，以此模擬吊籠內貝類的不同養殖密度（此處養殖密度指每層中的貝殼個數除以吊籠的層面積）。設置3組養殖密度，分別為組Ⅰ（0個／m2）、組Ⅱ（226個／m2）和組Ⅲ（566個／m2）。

1.2 實驗設備及布置

實驗是在大連理工大學海岸和近海工程國家重點實驗室小波流水槽（長22 m，寬0.45 m，高0.6 m）中進行（圖2）。實驗水深0.45 m，水槽尾部布置消能裝置，用以吸收波浪能量以減少波浪反射。三維測力計量程為10 N，兩支水下拉力計量程為1 N，測力計精度均為0.01 N。波高儀采用TWG—600型測量儀，實驗前先進行標定，標定線性度大于0.99。水流速度用聲學多普勒點式流速儀（ADV）進行測量，儀器分辨率0.01 cm／s。

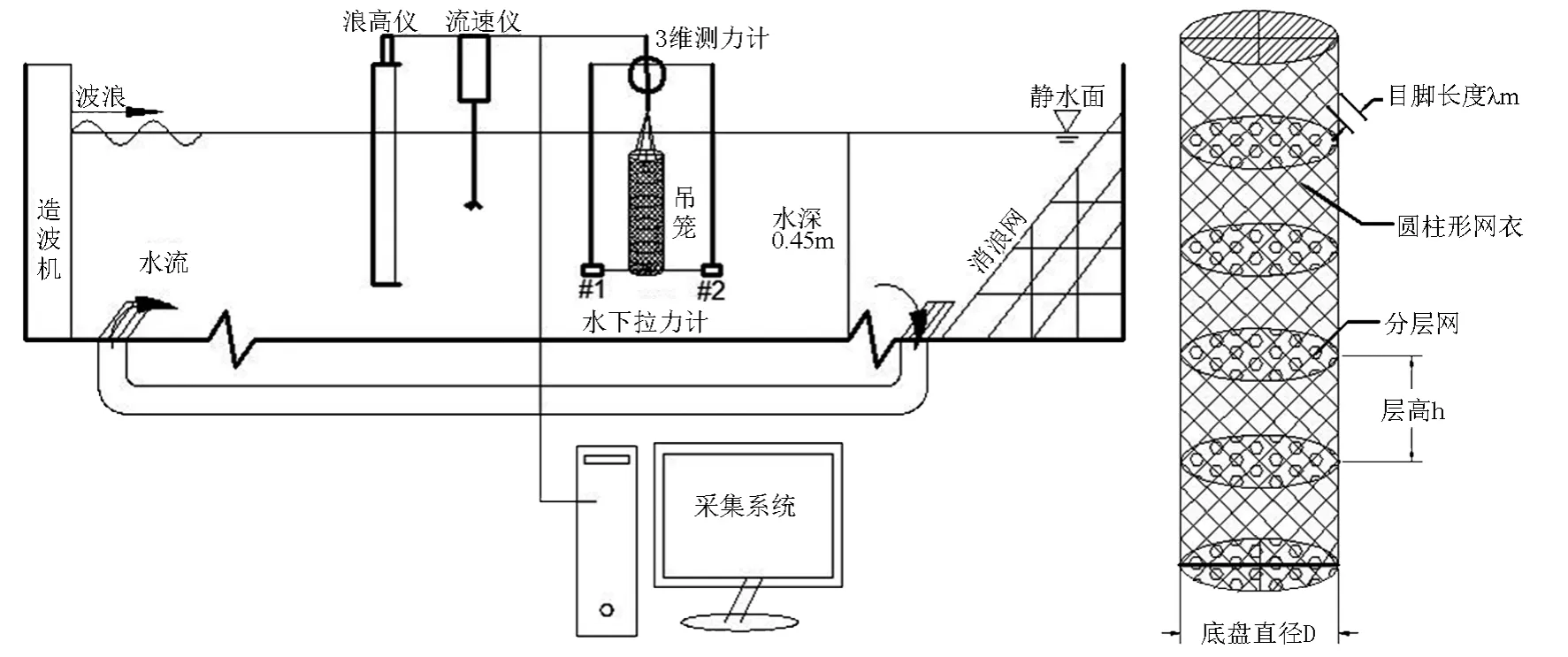
圖2 模型布置示意圖Fig.2 Layout diagram of the model

吊籠布置在水槽中部，吊籠頂端距水面0.05 m，左右距離槽壁均為0.15 m。布置形式分2種：固定式（三點約束），即吊籠上端懸掛于三維測力計，底部用兩支水下拉力計水平約束，在波浪或水流作用下保持不動；懸吊式（單點約束），即吊籠僅僅通過上端吊繩懸掛于三維測力計上。實驗數據全部由計算機自動采集和處理，采樣間隔均為0.01s，每組工況至少重復3次，取平均值為實驗最終結果。實驗采用的波浪要素見表1。設置5組實驗流速，分別為6.0、11.8、18.1、22.2和24.8 cm／s。

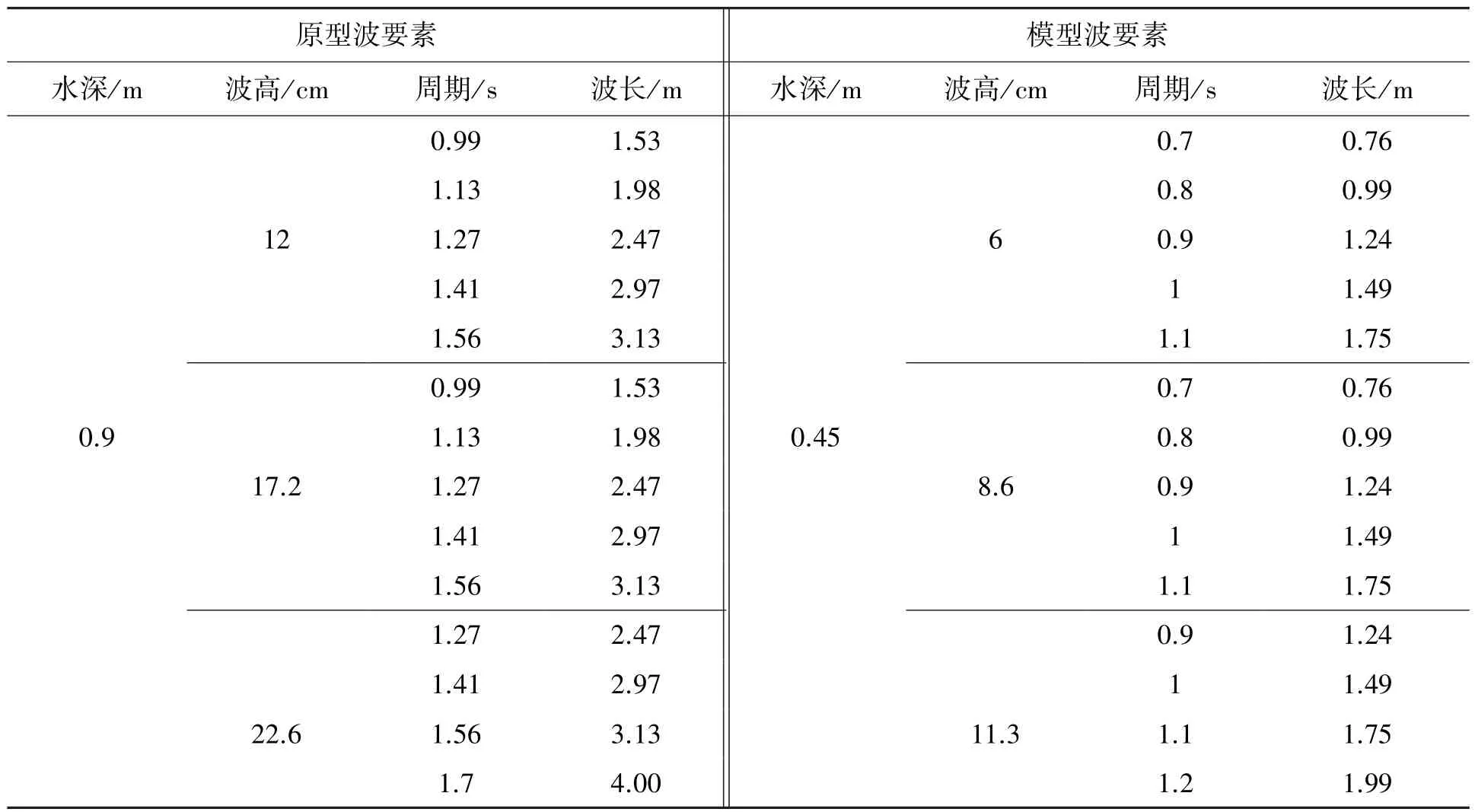
表1 原型與模型波要素表Tab.1 Wave parameters in prototype and model

1.3 水動力系數求解方法

本實驗條件下，僅對固定式吊籠進行水動力系數計算。吊籠直徑D與波長L相比很小，作用在吊籠上的水平波浪力F可以按照Morison方程進行計算。由于吊籠為鏤空體結構，故不能直接按照同等大小的實心圓柱進行求解，需要對方程中的柱體體積和柱體投影面積進行重新定義。Morison方程改寫如下：

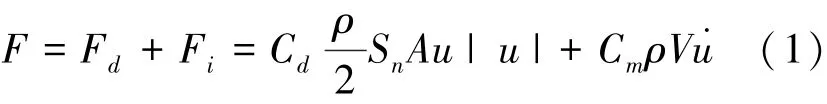
式中：Fd和Fi分別為速度力和慣性力，N；Cd和Cm分別為速度力系數和慣性力系數（無因次）；u和分別為水質點的瞬時速度與瞬時加速度，m／s，m／s2；ρ為流體密度，kg／m3；A為吊籠沿水平方向輪廓投影面積，m2；Sn為吊籠側面圓柱形網衣密實度［17］，經計算取為0.25；V是吊籠的排水體積，m3。本文通過排水法測得不同養殖密度下吊籠的排水體積V分別為0.075×10－3、0.22×10－3和0.435×10－3m3。

求解水動力系數的關鍵在于確定與吊籠受力對應的波浪的瞬時速度與瞬時加速度，這通常需要采用合適的波浪理論，在本實驗條件下采用一階線性波理論［18］進行求解。水平速度u和水平加速度計算公式如下：

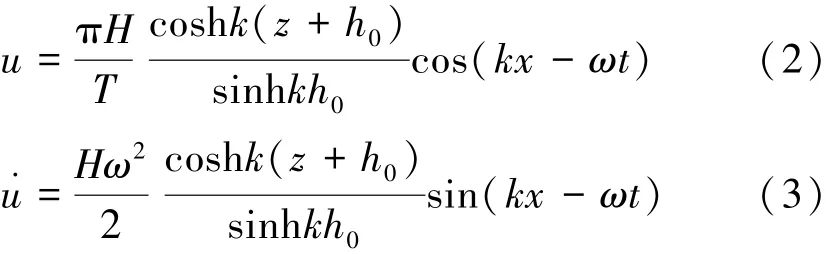
式中：H為波高，m；T為波周期，s；h0為水深，m；k為波浪的波數，m－1；ω為波浪圓頻率，rad／s；色散方程ω2＝gktanhkh0；x，z分別為水平和垂直坐標，m；靜止水位z＝0；t表示時刻，s。假設力的瞬時實測值Fm（N），力的計算值Fc（N），則兩者誤差平方和為：

式中：n為實測數據點個數；i表示第i時刻，s。

由最小二乘法，選用的Cd與Cm值應使Q→Qmin，為此應有，從而可求出水動力系數Cd和Cm。將利用最小二乘法獲得的吊籠水動力系數值代入Morison方程，可得吊籠的波浪力計算值。根據圖3，吊籠所受到的波浪力過程線計算值與實測值符合良好。

圖3 波浪力實測值與計算值的比較Fig.3 Comparison of the measured wave forces and the calculated wave forces

在純流條件下，方程僅剩速度力項，吊籠的速度力系數Cd可按如下公式計算：

通常取Kc、Re作為水動力系數分析的重要參數。當吊籠結構的特征長度λ取為吊籠的網線直徑時，式（6）和式（7）可以較好地表示吊籠直徑相同但網線直徑不同時的Kc與Re。

式中：umax取為吊籠中心點處水質點水平速度幅值，m／s；γ為水的運動粘性系數，m2／s；μ為水的動力粘滯系數，取為1.5×10－3kg／（m·s）。

2 結果

2.1 波浪和水流對吊籠受力的影響

當波高一定時，周期增加則吊籠受到的水平波浪力峰值隨之增大；當周期相同時，波高增大則吊籠受到的水平波浪力峰值增大；在同一波況下，貝類養殖密度越大則吊籠所受到的水平波浪力峰值越大（圖4a）。

圖4 波浪或水流作用下吊籠的水平受力圖Fig.4 Horizontal force of lantern net under wave or current loads

在波浪周期等于1 s（即頻率為1 Hz）時，吊籠的波浪力幾乎為最大，這可能是由于吊籠的自振頻率也在1Hz附近，兩者共振所致。流阻力F與來流速度u0基本呈冪函數關系，當養殖密度一定時，流阻力隨著流速的增大而增大；在相同流速下，隨著養殖密度的增大，流阻力也相應增大（圖4b）。

2.2 波浪和水流對吊籠運動的影響

在吊籠中心位置及底部各安裝一個發光二極管作為示蹤光源，通過專用動態圖像采集分析軟件［19］進行運動分析。吊籠會隨浪左右搖擺，隨流出現穩定傾角。吊籠傾角θ為吊籠繞懸吊點偏移最大位置與豎直方向的夾角。當波高一定時，周期增大則吊籠傾角增大；當周期相等時，波高增大吊籠傾角亦增大；在同一波況下，隨著養殖密度增大吊籠傾角相應減小（圖5）。在同一養殖密度下，流速越大，吊籠傾角越大；在相同流速下，隨著養殖密度的增大，吊籠傾角相應減小（圖6）。

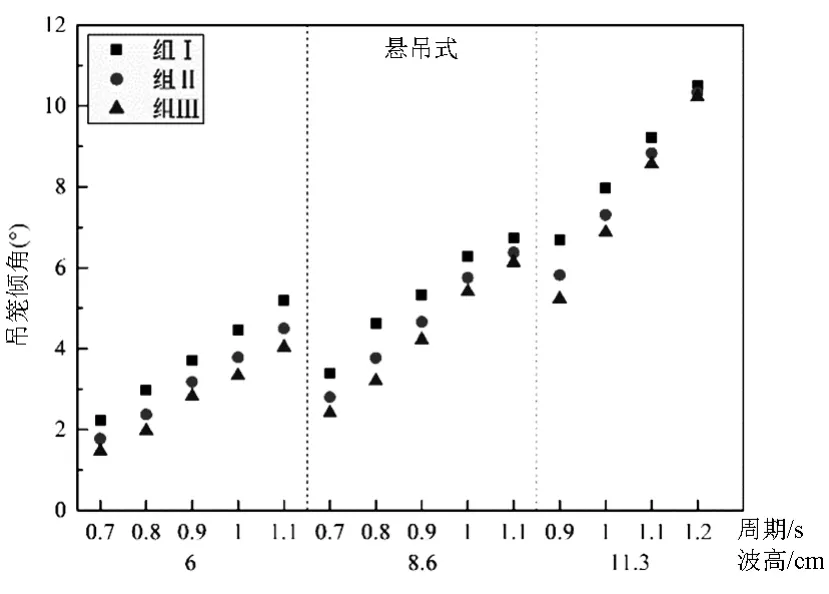
圖5 吊籠傾角與波高－周期關系圖Fig.5 Periodic relationship between the dips and wave height

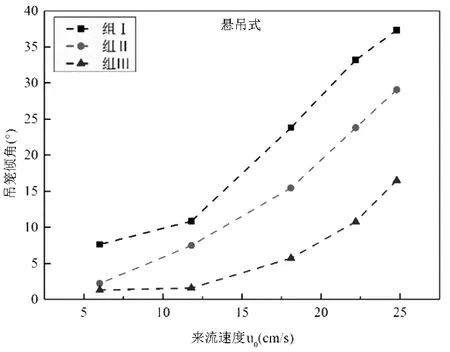
圖6 吊籠傾角與流速關系圖Fi .g6 Relationship between the dips and current velocity

2.3 吊籠對周圍流場的影響

實驗采用ADV流速儀測量吊籠背流側距中心點45 cm（即3倍吊籠直徑）處的流速數據。在同一養殖密度下，隨著來流速度的線性增加，3倍吊籠直徑后的流速大致呈線性增大；當流速一定時，隨著養殖密度的增加，吊籠背流側同一位置處的流速呈下降趨勢（圖7a）。

定義一個無量綱參數—流速衰減因子γ＝u／u0來表示吊籠對流場的影響。隨著來流速度的增大，流速衰減因子也有逐漸增大趨勢，3倍吊籠直徑后的流速大致衰減到來流速度的35%～ 55%。這表明吊籠的阻流效果隨著流速增大而變弱（圖7b）。

2.4 吊籠的水動力系數

當養殖密度一定時，在波浪作用下，隨著Kc數和Re數的增大，速度力系數Cd略微增大，而慣性力系數Cm則先增大后趨于常數（圖8、圖9）；在純流作用下，隨著雷諾數的增大，速度力系數Cd值略有改變（先減小后增大），但總體平穩（圖10）。在相同工況下，隨著養殖密度的增大，速度力系數Cd增大而慣性力系數Cm減小。

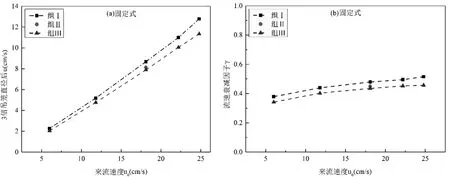
圖7 不同養殖密度下距吊籠中心點45 cm處流速值Fig.7 The flow－velocity at 45 cm away from the center of lantern net under different breeding densities

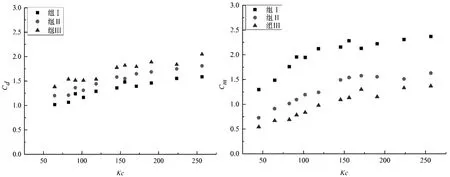
圖8 波浪作用下Cd、Cm與Kc數關系圖Fig.8 The relationship betweenKcandCd，Cmunder wave action

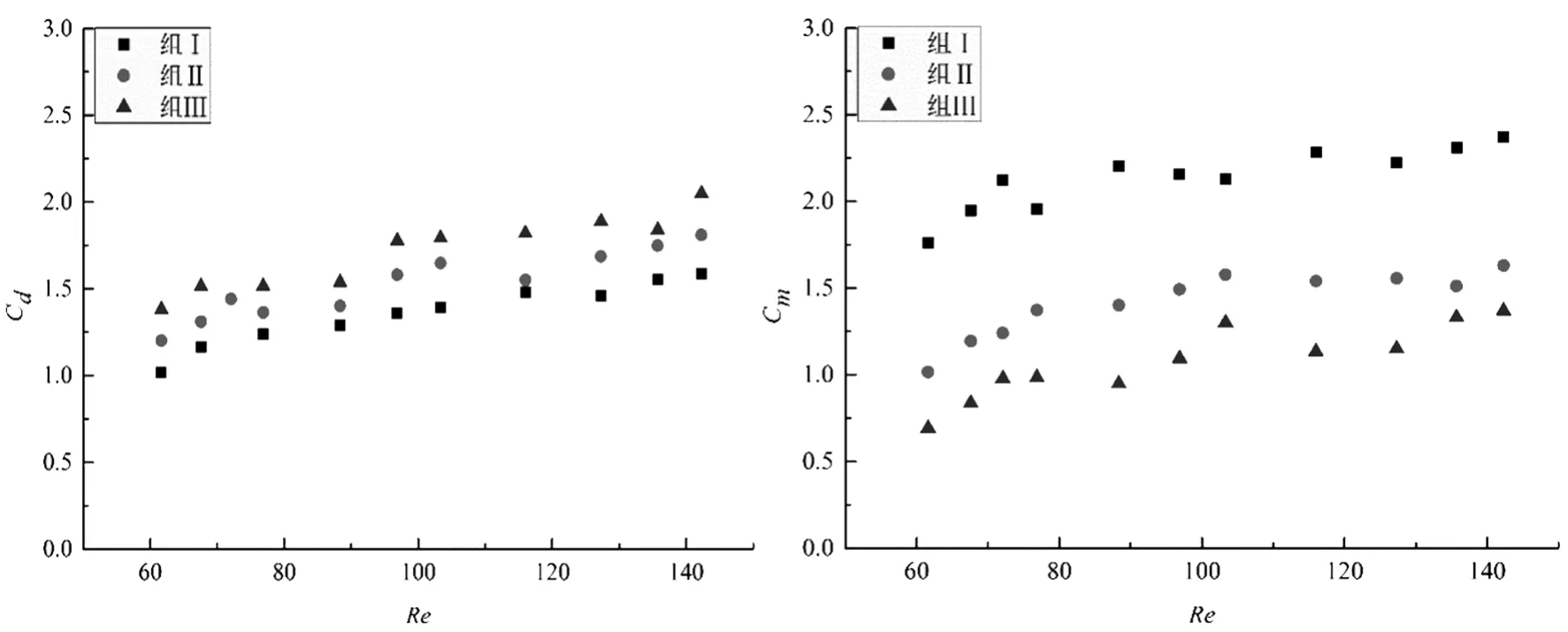
圖9 波浪作用下Cd、Cm與Re數關系圖Fig.9 The relationship betweenReandCd，Cmunder wave action

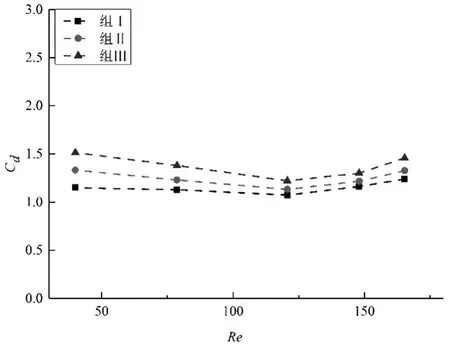
圖10 水流作用下Cd與Re數關系圖Fig.10 The relationship betweenReandCdunder current action

3 討論

在海洋環境下，吊籠主要受波浪和水流荷載作用。Morison方程是小尺度構件波流力的實用計算方法，對于不同結構運用Morison方程時水動力系數取值一般不同，故吊籠水動力系數的正確選取將直接關系到筏式養殖設施結構設計及整體優化。由于吊籠是透空結構圓柱，其透水性主要受網衣密實度和貝類養殖密度影響。故張光發［20］將之簡化為實圓柱體估算波流力偏于保守。本實驗建議，在純浪效應下，當吊籠空載（即養殖密度為0個／m2）時，Cd和Cm值可分別取為1.5和2.2；當養殖密度為566個／m2時，Cd和Cm值可分別取為1.8和1.3；在純流效應下，當吊籠空載（即養殖密度為0個／m2）時，Cd值可取為1.2；當養殖密度為566個／m2時，Cd值可以取為1.5。本實驗得到的速度力系數值小于田內［9］給出的經驗系數1.76。原因有：一是相同網面積下的圓形網片流阻力小于平面網片的流阻力［11］；二是現代漁具中廣泛應用的合成纖維網要比以往的植物纖維網具有更好的濾水性，其水阻力系數也就顯著減小［21］。

4 結論

本研究結果表明，吊籠的運動及受力隨著波高、周期及流速的增大而增大。貝類養殖密度增大，則吊籠受到的水平力增大，運動幅度減小。在波浪效應下，隨著Kc數、雷諾數Re的增大，速度力系數Cd有略微增大趨勢，而慣性力系數Cm則先增大后趨于常數。在水流效應下，速度力系數Cd值隨著雷諾數Re的增大無顯著變化。在相同工況下，隨著貝類養殖密度的增加，速度力系數Cd增大，而慣性力系數Cm減小。本研究通過實驗獲得的貝類養殖吊籠在波浪、水流及不同養殖密度下的水動力系數，可在計算吊籠波浪力和流阻力時為水動力系數的取值提供參考。 □

［1］ 張繼紅，王巍，蔣增杰，等.桑溝灣夏季櫛孔扇貝養殖籠內水質變化［J］.漁業科學進展，2010（4）：9－15.

［2］ 李明智，張光發，鄧長輝，等.蝦夷扇貝浮筏養殖作業改造與試驗［J］.農業工程學報，2014（11）：195－204.

［3］ 蔣增杰，方建光.附著生物對貝類養殖的影響及其防除［J］.南方水產，2005，1（3）：65－68.

［4］ 李玉成，滕斌.波浪對海上建筑物的作用［M］.北京：海洋出版社，2015：303.

［5］ 交通運輸部.JTS145－2015港口與航道水文規范［S］.北京：2015.

［6］ FU E B，SATO O，NASHIMOTO K，et al.Wave force action on plane nets［J］.Nippon Suisan Gakkaishi，1989，55（1）：65－75.

［7］ ZHAO Y，LI Y，DONG G，et al.An experimental and numerical study of hydrodynamic characteristics of submerged flexible plane nets in waves［J］.Aquacultural Engineering，2008，38（1）：16－25.

［8］ LIU LL，KINOSHITA T，WAN R，etal.Experimental investigation and analysis of hydrodynamic characteristics of a net panel oscillating in water［J］.Ocean Engineering，2012，47：19－29.

［9］ 桂福坤.深水重力式網箱水動力學特性研究［D］.大連：大連理工大學，2006：77－78.

［10］BALASH C，COLBOURNE B，BOSE N，et al.Aquaculture Net Drag Force and Added Mass［J］.Aquacultural Engineering，2009，41（1）：14－21.

［11］詹杰民，胡由展，趙陶，等.漁網水動力試驗研究及分析［J］.海洋工程，2002（2）：49－53.

［12］李冠穎.外海浮筏式蚵架動力分析［D］.高雄：國立中山大學，2010：55－58.

［13］PLEW D R，ENRIGHT M P，NOKES R I，et al.Effect of mussel bio－pumping on the drag on and flow around a mussel crop rope［J］.Aquacultural Engineering，2009，40（2）：55－61.

［14］周應祺.漁具力學［M］.北京：中國農業出版社，2001：140－144.

［15］LEAVITTD.Grow－out culture of the bay scallop［R］.Maryland：Northeast Regional Aquaculture Center，2010：1－10.

［16］SURIER A，KARNEY R，GUO X，et al.CREATING A TETRAPLOID BROODSTOCK FOR THE BAY SCALLOP，ARGOPECTEN IRRADIANS［J］.JournalofShellfish Research，2009，28（3）：657.

［17］BI C，ZHAO Y，DONG G，et al.Experimental investigation of the reduction in flow velocity downstream from a fishing net［J］.Aquacultural Engineering，2013，57（6）：71－81.

［18］鄒志利.水波理論及其應用［M］.北京：科學出版社，2005：17－25.

［19］GUI F，LI Y，DONG G，et al.Application of CCD image scanning to sea－cage motion response analysis［J］.Aquacultural Engineering，2006，35（2）：179－190.

［20］張光發，黃亞南，梁峻，等.外海延繩式浮筏養殖設施抗風浪能力估算方法研究［J］.漁業現代化，2014，41（6）：22－27.

［21］虞聰達，朱江忠，何千軍.聚乙烯平面網片水動力特性研究［J］.浙江水產學院學報，1991，10（1）：40－45.

Experimental study on hydrodynamic characteristics of lantern net for shellfish culture

ZHAO Yunpeng1，LIAO Peng1，BI Chunwei1，LI MingZhi2
（1 State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian 116024，China；2 College of Navigation and Shipbuilding Engineering，Dalian Ocean University，Dalian 116023，China）

In this paper，hydrodynamic characteristics of lantern net under regular wave and uniform current are respectively discussed by model test，and the influence of different densities of shellfish on the force of lantern net is analyzed.The hydrodynamic coefficientsCdandCmare calculated by the least square method based on the Morison equation under wave load；Drag coefficientCdis calculated using the simplified Morison formula in the effect of current；and the effects ofKcnumber，Reynolds number and breeding density of shellfish on hydrodynamic coefficientsCdandCmare analyzed.The results indicate that：The motion amplitude and force of the lantern net increase with the increase of the wave height，period and current velocity；The horizontal force of lantern net increases and the amplitude of the motion decreases as the shellfish breeding density increases；Drag coefficientCdincreases slightly with theKcnumber and the Reynolds number increases under wave load，while inertia coefficientCmincreases first and then remains stable；The drag coefficientCddoes not change significantly with the increase of Reynolds number under current action；Under the same conditions，the increase of shellfish breeding density leads to the increase of drag coefficient and decrease of inertia coefficient.The study shows that，the hydrodynamic coefficients for the lantern net obtained from this experiment could be used as reference in the calculation of wave and current loads of lantern nets.

lantern net；hydrodynamic coefficients；regular wave；uniform current；breeding density

S953.5

A

1007－9580（2017）02－006－08

10.3969／j.issn.1007?9580.2017.02.002

2017－01－05

國家自然科學基金（51239002，51579037，51221961，51609035）；中國博士后基金（2016M590224）；中央高校基本科研業務費專項（DUT16YQ105）

趙云鵬（1980—），男，教授，研究方向：筏式養殖設施水動力特性。E－mail：Ypzhao＠dlut.edu.cn