采用Gabor濾波簇和等距映射算法的織物疵點檢測方法

王傳桐， 胡 峰， 徐啟永， 吳雨川， 余聯慶

(武漢紡織大學 機械工程與自動化學院， 湖北 武漢 430074)

采用Gabor濾波簇和等距映射算法的織物疵點檢測方法

王傳桐， 胡 峰， 徐啟永， 吳雨川， 余聯慶

(武漢紡織大學 機械工程與自動化學院， 湖北 武漢 430074)

為提高織物疵點檢測率，將Gabor濾波法與等距映射方法進行融合，克服疵點檢測過程中存在的問題。首先用由3個尺度和5個方向組成的15個Gabor濾波器簇對織物疵點圖像進行濾波，減少疵點圖像光照不均和對比度低的影響；然后將濾波圖像劃分成面積相等且互不重合的鄰域，并從鄰域中提取高維特征向量。采用等距映射方法對高維特征向量進行降維，剔除高維特征中冗余信息，強化分類器擬合能力；再用低維嵌入模型提取新增樣本低維特征向量，用于概率神經網絡分類器分類，檢測是否存在疵點；最后用2種不同紋理的織物進行檢測實驗。結果表明，本文方法能有效提高疵點的檢測精度。

疵點檢測； Gabor濾波簇； 等距映射； 圖像處理

中國是紡織品生產大國，提高紡織品疵點檢測準確率對提升紡織品質量和競爭力具有重要意義。小波分析法是常用的疵點檢測手段之一[1]。

離散正交小波具有快速Mallat算法支持，適合紋理的實時分析[2]。它從3個方向(0°、45°、90°)進行多尺度織物圖像分解。在小波基和尺度選擇合適的情況下，織物背景紋理將被抑制，疵點邊緣能顯著增強，但是，正交離散小波進行疵點圖像分解時會出現明顯相位畸變，不利于疵點檢測[3]。復輪廓變換法比離散正交小波更具優勢，該方法核心是雙樹復小波變換和方向濾波器[4]，可在6個方向(±15°、±45°、±75°)下對疵點圖像進行不同尺度分解，并且雙樹小波是復小波，回避了正交離散小波相位畸變的缺點。與前2種小波方法相比，Gabor小波的方向和尺度不受限制，并且和雙樹小波一樣也屬于復小波。用多尺度、多方向的Gabor濾波簇對疵點圖像進行濾波，能夠提高疵點圖像對比度，抑制正常紋理信息和噪聲[5-6]。通常情況下，Gabor小波實部用于平滑疵點圖像，虛部用于檢測疵點邊緣[7]。Gabor濾波函數通過剔除直流分量，使其具有對光照變化不敏感的特點，但是，最優Gabor小波濾波器設計困難，基于Gabor濾波簇的疵點特征向量又具有維數高和冗余信息大的缺點[7]。等距映射算法(Isomap)是非線性降維方法，它能保持數據在空間中的幾何結構，可獲得高維特征向量本質維數[8]，有助于克服基于Gabor濾波簇特征向量的維數高和冗余信息大的缺點。

本文將2種方法結合用于織物疵點檢測，并提出Isomap結構參數的優化方法和新增樣本的低維嵌入模型，以用于提高疵點的檢測準確率。

1 織物疵點檢測算法

圖1示出疵點檢測流程圖。

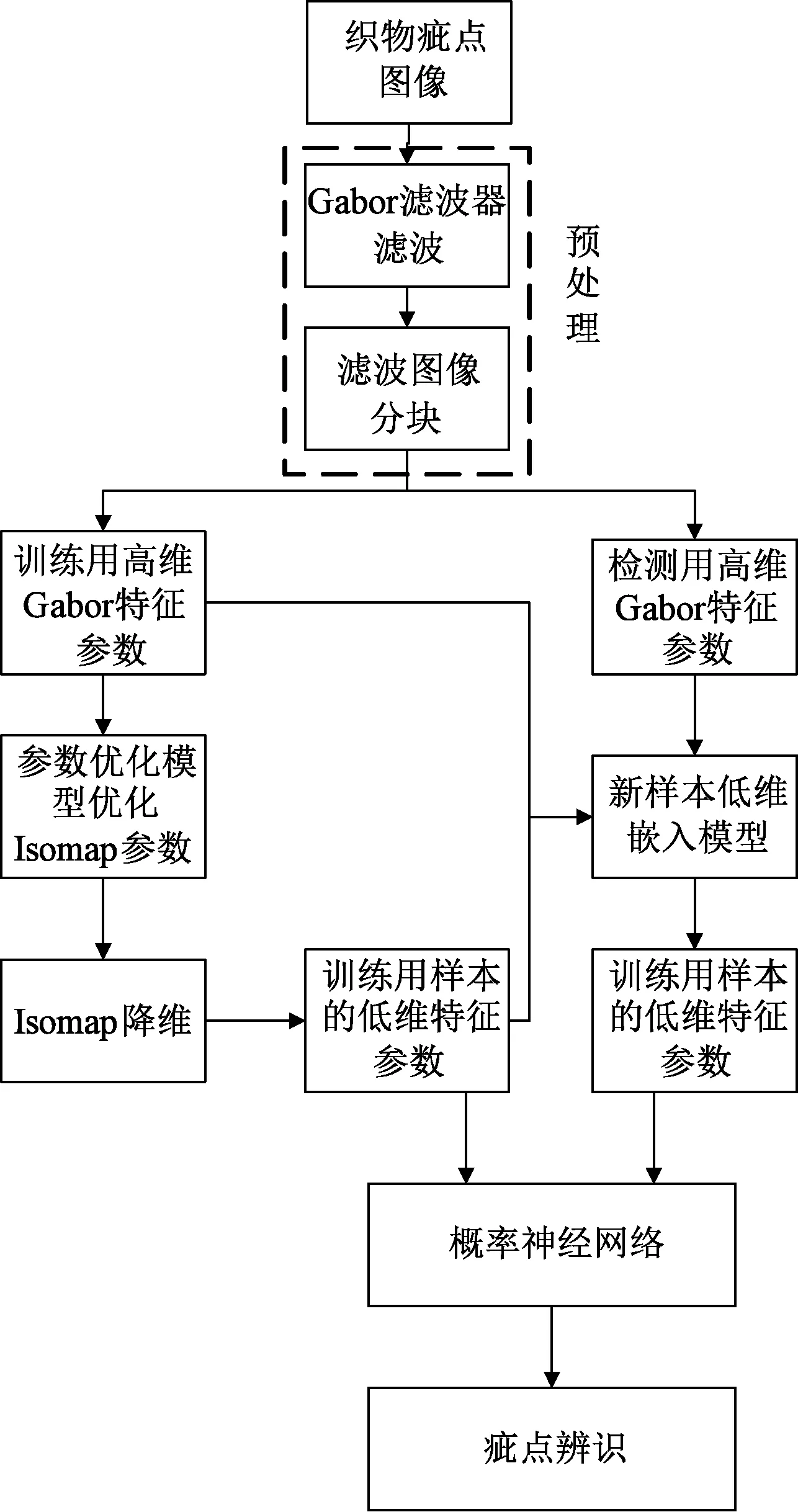
圖1 疵點檢測流程圖Fig.1 Flow chart of fabric detection

步驟1：利用Gabor濾波簇進行高維特征向量提取。

2)將疵點灰度圖I和Gabor濾波器進行卷積，生成15張濾波圖像。濾波后的疵點圖像可表示為

(1)

式中?表示卷積算子。

3)將每張濾波圖像劃分成N個尺寸為M×M互不重疊的子窗口。

4)針對灰度圖子窗口I(a,b)(第b行a列子窗口)，將15張濾波圖像中相同位置子窗口Fλθ(a,b)的灰度值依次連接組成高維特征向量，向量維數為M×M×15。

步驟2：訓練樣本的降維。

使用Isomap算法[10]對高維特征向量進行降維，消除冗余信息，有助于降低分類器泛化能力和提高分類器擬合能力，達到提高分類器分類精度的目的。降維過程中，嵌入維數d和鄰域大小k會影響降維精度。因此，采用離散粒子群算法[11-12]進行參數優化。適應度函數采用Ncut準則[13-14]：

(2)

(3)

式中，織物樣本分為2類(正常樣本和疵點樣本)，Ci是屬于類i的樣本集合，S(xi,xj)是樣本xi和xj間的邊權值，d(xi,xj)是xi和xj間的歐式距離，σi(σj)是xi(xj)與鄰域點的平均距離。如果樣本xi和xj之間沒有邊，則邊權值為零。由式(3)可知，S∈[0,1]，它使不同維度空間計算得到的邊權值具有可比性，從而使用于衡量類可分性的Ncut值在不同維度空間具有可比性。當類Ci邊界點與其他類邊界點相距越遠，邊權值S越小，式(2)的分子越小；當類內Ci數據點相互越靠近時，邊權值S越大，式(1)的分母越大。Ncut值越小時，類可分性越好。

1)初始化離散粒子群參數。設置種群大小為22，粒子維數為30，最大迭代次數為100。

2)利用Isomap算法計算訓練樣本的低維輸出向量。計算每個粒子適應度值，獲取最佳嵌入維數和鄰域大小。運用Isomap算法，使用得到的嵌入維數和鄰域值對訓練樣本進行降維，得到訓練樣本的低維嵌入結果。

步驟3：驗證樣本的降維。

輸入新樣本xnew，它在訓練樣本集中k個最近鄰點為xj，j=1,2,…,k。yj為xj的低維輸出向量。X=[x1,x2,…,xk]為高維訓練樣本集合，Y=[y1,y2,…,yk]為訓練樣本低維特征向量。首先找出新樣本在訓練樣本集中的k個鄰近點。然后計算xnew和xj間的權值wij[15]。最后利用式(4)計算新樣本的低維特征向量ynew。

(4)

步驟4：疵點檢測。

1)使用訓練樣本對概率神經網絡(PNN)[16]進行訓練，將訓練樣本中正常樣本的低維特征向量、疵點樣本的低維特征向量輸入概率神經網絡進行訓練。

2)將驗證樣本的低維特征向量輸入概率神經網絡進行分類，并對存在疵點的子窗口進行標注。

2 實驗結果與分析

在相同條件下，將5種方法進行對比實驗研究，驗證本文方法的合理性和有效性。這5種方法如下所示。

1)本文提出的基于Gabor小波與Isomap方法相結合的疵點檢測方法(簡稱Isomap方法)。

2)基于Gabor小波和灰度共生矩陣疵點檢測方法(簡稱Gabor方法)。該方法利用Gabor濾波簇進行預處理的部分與方法1相同。不同之處在于：對每個子窗口提取4個方向(0°,45°,90°,135°)的對比度、能量、熵和相關性，共計16個特征。然后，將15張濾波圖像中相同位置子窗口獲得的16個特征依次連接組成高維特征向量，向量維數為240。

3)基于Gabor小波、灰度共生矩陣和主成分分析(PCA)相結合的檢測方法(簡稱G-PCA方法)。該方法采用PCA對方法2中高維特征向量進行降維。降維過程中選取出特征值占總特征值0.85以上的相互正交的特征值。

4)基于Gabor小波和PCA相結合檢測方法(簡PCA方法)。該方法利用Gabor濾波簇進行預處理的部分與方法1相同。不同之處在于：用PCA方法取代Isomap方法進行降維。降維過程中選取出特征值占總特征值0.85以上的相互正交的特征值。

5)基于Gabor小波、灰度共生矩陣和Isomap方法相結合的檢測方法(簡稱G-Isomap方法)，該方法與方法3近似，不同之處在于：利用Isomap方法取代PCA方法對方法2中高維特征向量進行降維。

研究樣本來源于自建的Fabric Defects Database of WTU數據庫中E1子數據庫(平紋組織；緯密為256根/10 cm；經密為256根/10 cm；線密度為15.63 tex；采集分辨率為0.044 mm/像素)和E2子數據庫(平紋組織；緯密為264根/10 cm；經密為340根/10 cm；線密度為14.08 tex；采集分辨率為0.089 mm/像素)。2個子數據庫中包含雜經、缺經、破洞、油污、粗緯和竹節等疵點類型，疵點灰度圖尺寸為300像素×300像素。分別從子數據庫中選取40張圖片作為訓練樣本集，每類疵點圖片數量為10張；20張圖片作為驗證樣本集，每類疵點圖片數量為5張。

利用式(5)計算驗證樣本集的疵點分類準確率。

(5)

式中：R為準確識別率；Pr為準確識別子窗口個數；PA為識別子窗口總數。

使用5種方法對E1、E2數據庫中織物疵點進行疵點對比檢測，疵點識別過程中分別選用尺寸為25像素×25像素、30像素×30像素和50像素×50像素的子窗口，研究子窗口尺寸對檢測精度的影響。

表1示出5種方法對E1數據庫的疵點檢測準確率。表2示出5種方法對E2數據庫的疵點檢測準確率。圖2示出在子窗口大小為30像素×30像素時，5種方法對E1數據庫的部分檢測結果。圖3示出在子窗口大小為30像素×30像素時，5種方法對E2數據庫的部分檢測結果。

觀察表1、2發現：在不同尺度下，PCA方法對E1和E2數據庫的檢測準確率大約在70%～77%之間；而Isomap方法對E1和E2數據庫的檢測準確率在94%～98%之間，明顯高于PCA方法。2種方法的高維特征向量提取方法相同，造成檢測準確率相差較大的原因可能是：由灰度值構成的高維特征向量在高維空間不是分布在一個超平面上，而是分布在一個曲面流形上。PCA方法是一種線性降維方法，只能對分布在超平面上的數據進行有效降維；對分布在曲面流形上的數據點，降維過程中可能將它們映射到低維空間中同一個點上，降低了類的可分性；而Isomap方法屬于非線性降維方法，在降維過程中可保持流形的全局幾何結構，并且利用Ncut準則進行參數優化，增加了低維特征向量在低維空間的類可分性。因此，使Isomap方法的識別精度高于PCA方法。Gabor方法、G-PCA方法和G-Isomap方法對2個數據庫在不同尺度下的識別準確率都在90%以上，其中G-Isomap方法的檢測準確率最高，在94.2%～98%之間。G-PCA方法最低，在90%～95%之間，Gabor方法居中，在93%～96.7%之間。3種方法檢測準確率相差不大，主要原因在于Gabor簇對疵點圖片進行不同尺度和方向濾波后，增加了疵點和正常區域的對比度，消除光照不均的影響，提高基于灰度共生矩陣特征值(對比度、能量、熵和相關性)的靈敏度。由這些特征值組成的高維特征向量自身對疵點區域具有較高靈敏度，且特征維數固定，不受子窗口尺度的影響，不會強化PNN神經網絡輸入層和樣本層的泛化能力，降低樣本層和競爭層間的擬合精度，導致分類器分類精度下降。Gabor方法檢測準確率比G-PCA方法高的原因可能是：高維數據在數據空間呈弱非線性，PCA在降維過程中沒有完整保留高維特征向量的空間幾何結構和有效信息，使得低維特征向量靈敏度下降。G-Isomap方法使用Isomap方法降維，可克服高維特征向量非線性影響，并有效地從高維數據中剔除冗余信息，降低了PNN神經網絡輸入層和樣本層間的計算難度，提高了樣本層和競爭層間的擬合精度，增加了分類器的分類準確性。G-Isomap方法和Isomap方法對2個數據庫的檢測準確率相差不大，都在94%～98%之間，說明Isomap方法降維能力很強，對特征向量維數不敏感。其次，G-Isomap方法中存在提取基于灰度共生矩陣特征值的環節，在計算時間上肯定要比Isomap方法長，不利于疵點的快速檢測。

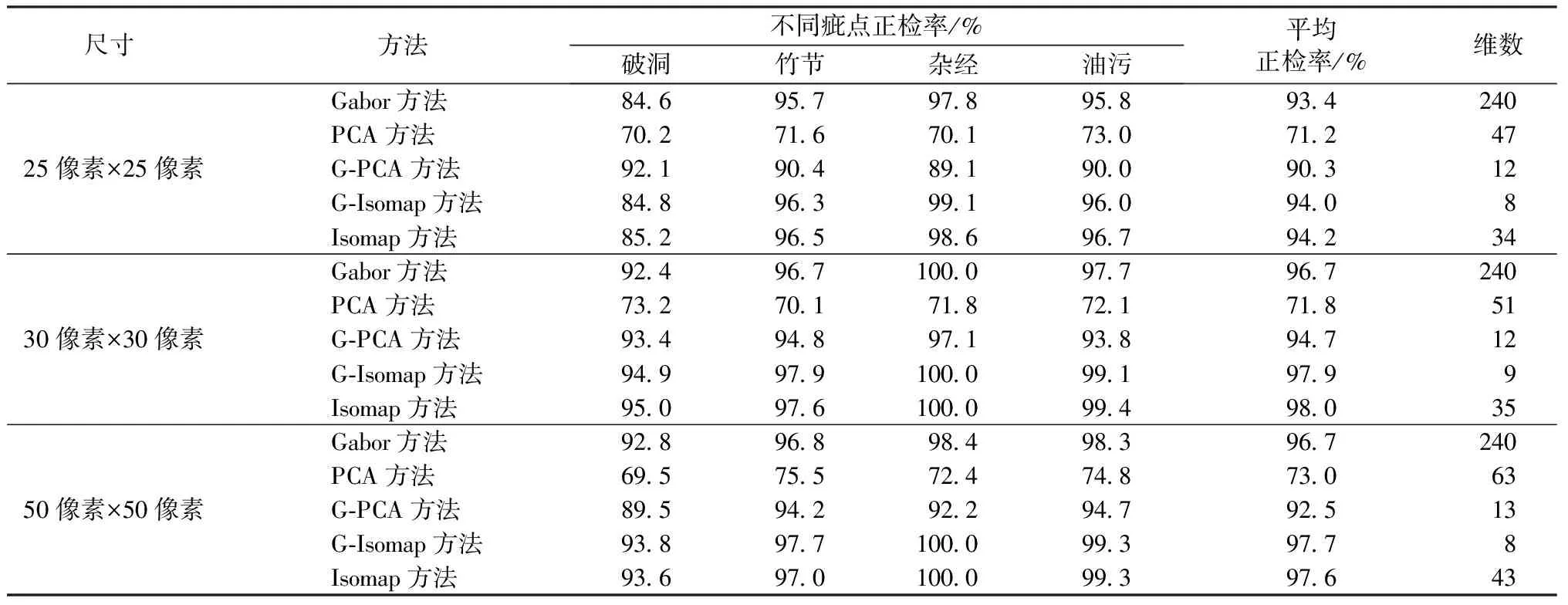
表1 數據庫E1辨識正檢率Tab.1 Recognition results positive detection rate of database E1

表2 數據庫E2辨識正檢率Tab.2 Recognition results positive detection rate of database E2

圖2、3分別示出數據庫E1(針對竹節疵點)、E2(針對粗緯疵點)的匹辨識效果。由圖可知：子窗口尺寸在30像素×30像素情況下，PCA方法正常紋理的誤判位置過多，導致該方法的檢測準確率較低；而Isomap方法誤檢位置數量明顯強于PCA方法。進一步說明PCA方法不適用于基于灰度值的高維特征向量降維。在相同子窗口尺寸下，在Gabor、G-PCA和G-Isomap方法對疵點檢測結果中發現：3種方法均存在少量的誤檢及漏檢位置，其中G-PCA方法中的誤檢數量略多于Gabor方法和G-Isomap方法。而G-Isomap方法誤檢數量比Gabor方法少，說明Isomap在對灰度共生矩陣特征向量降維更為有效，其低維特征向量具有更高的類可分性；與Isomap方法相比，PCA在對疵點特征降維過程中并不具備優勢。G-Isomap方法和Isomap方法的誤檢和錯檢數目基本相同，均可實現準確檢測，與表1和表2的統計結果一致。

圖2 數據庫E1針對竹節疵點的匹辨識效果Fig.2 Slab yarn identification effect of database E1

圖3 數據庫E2針對粗緯疵點的匹辨識效果Fig.3 Coarse pick identification effect of database E2

3 結 論

基于Gabor濾波器簇提出的高維特征向量呈現非線性，Isomap方法可克服非線性影響，剔除高維特征中冗余信息，弱化分類器的泛化性能，強化分類器的擬合性能，提高分類器的分類精度和疵點的檢測精度。利用Ncut進行Isomap方法的參數選擇，可增加低維特征向量的靈敏度和類可分性，有助于疵點檢測精度的提高。基于濾波圖像子窗口灰度值構造的高維特征經過Isomap方法降維后獲得的低維特征，在疵點檢測中具有較高的靈敏度。

FZXB

[1] 管聲啟, 石秀華. 基于頻域濾波的織物疵點檢測[J].計算機應用, 2008, 28(10):2673-2675. GUAN Shengqi，SHI Xiuhua. Fabric defects detection based on frequency domain filtering[J]. Journal of Computer Application, 2008, 28(10):2673-2675.

[2] 楊曉波. 基于自適應離散小波變換的混合特征畸變織物疵點識別[J]. 紡織學報，2013, 34(1):133-137. YANG Xiaobo. Research of mixture feature aberrance fabric defect recognition based on self-adaptive discrete wavelet transform[J]. Journal of Textile Research, 2013, 34(1):133-137.

[3] 李立輕. 基于計算機視覺的織物疵點自動檢測研究[D]. 上海：東華大學, 2003:2-4. LI Liqing. Study on computer vision-based automatic detection of fabric defects[D]. Shanghai: Donghua University, 2003:2-4.

[4] 槐向兵, 厲征鑫, 劉建立, 等. 基于輪廓波變換的織物疵點圖像消噪新方法[J]. 計算機工程與應用, 2014, 50(19):143-146. HUAI Xiangbing, LI Zhengxin, LIU Jianli, et al．New fabric defect image denoising method based on contourlet transform[J]．Computer Engineering and Applications, 2014,50(19):143-146.

[5] 屈博, 盧朝陽, 李靜, 等. 一種改進的多通道Gabor濾波器布匹瑕疵檢測方法[J].紡織學報，2009, 30(12):37-40. QU Bo, LU Zhaoyang, LI Jing, et al. An improved multichannel Gabor filter algorithm for fabric defect detection[J]. Journal of Textile Research, 2009, 30(12):37-40.

[6] JING Junfeng, YANG Panpan, LI Pengfei, et al．Supervised defect detection on textile fabrics via optimal Gabor filter[J]. Journal of Industrial Textiles, 2013, 44(1):40-57

[7] ZHENG Zhonglong，FAN Yang，TAN Wenan, et al. Gabor feature-based face recognition using supervised locality preserving projection[J]. Signal Processing, 2007, 87(10):2473-2483

[8] YAN Deqin, LIU Shenglan, LI Yanyan. An embedding dimension reduction algorithm based on sparse anal-ysis[J]. Acta Automatica Sinica, 2011, 37(11): 1306-1312.

[9] AJAY Kumar, GRANTHAM Pang. Defect detection in textured materials using Gabor filters[C]. Industry Applications IEEE Transactions on, 2002, 38(2):425-440.

[10] WANG L，ZHANG Y，FENG J. On the Euclidean distance of images[J]. IEEE Trans on Pattern Analysis and Machine Intelligence,2005,27(8):1334-1339.

[11] LIU Yan, GU Xueping. Skeleton-network reconfiguration based on topological characteristics of scale-free networks and discrete particle swarm optimization [J]. IEEE Transactions on Power Systems, 2007, 22(3):1267-1274.

[12] ALBERTO García-Villoria, RAFAEL Pastor. Introducing dynamic diversity into a discrete particle

swarm optimization [J]. Computer and Operation Research, 2009, 36(3):951-966.

[13] 胡峰, 蘇訊, 劉偉, 等. 基于改進局部線性嵌入算法的故障特征提取方法[J]. 振動與沖擊，2015, 34(15):201-204. HU Feng, SU Xun, LIU Wei, et al. Fault feature extraction based on improved locally linear embe-dding [J]. Journal of Vibration and Shock, 2015, 34(15):201-204.

[14] 胡峰, 王傳桐, 吳雨川, 等. 基于改進監督LLE算法的故障特征提取方法[J]. 振動與沖擊，2015(21):119-123. HU Feng, WANG Chuantong, WU Yuchuan, et al. Fault features extraction based on improved supervised locally linear embedding [J] Journal of Vibration and Shock, 2015(21):119-123.

[15] LIANG Dong, YANG Jie, ZHENG Zhonglong. A facial expression recognition system based on supervised locally linear embedding[J]. Pattern Recognition Letters, 2005, 26(15):2374-2389.

[16] 史峰, 王小川, 郁磊, 等. MatLab神經網絡30個案例分析[M]. 北京:北京航空航天大學出版社,2010：197-182. SHI Feng, WANG Xiaochuan,YU Lei, et al. 30 Case Analysis of MatLab Neural Network[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2010：197-182.

Detection of fabric defects based on Gabor filters and Isomap

WANG Chuantong, HU Feng， XU Qiyong， WU Yuchuan， YU Lianqing

(SchoolofMechanicalEngineeringandAutomation,WuhanTextileUniversity,Wuhan,Hubei430074,China)

In order to improve the correction rate of fabric defects, Gabor filters and Isomap were used to detect the fabric defect. Firstly, the images of fabric defect were filtered by 15 Gabor filters with 3 orientations and 5 scales, which contributed to overcome the effect of uneven illumination and low contrast. Then, the filtered images were divided into non-overlapping rectangular patches and high-dimensional features were extracted. Simultaneously, Isomap algorithm was applied to reduce the dimensionality of feature and eliminate the redundant information. Besides, a mapping model of new samples was proposed to detect the low dimensional embedding results. Finally, the performance of proposed algorithm was estimated off-line by two sets of fabric defect images. The theoretical argument is supported by experimental results.

fabric defect detection； Gabor filter； Isomap； image processing

2016-03-25

2016-12-13

國家自然科學基金資助項目(51205294；61271008；51275363)

王傳桐(1991—)，男，碩士生。主要研究方向為紡織品質量檢測和模式識別。胡峰，通信作者，E-mail：hufeng@wtu.edu.cn。

10.13475/j.fzxb.20160305306

TP 311.131； TS 101.97

A