非等間距GM(1，1)模型的性質(zhì)研究

何敏藩，曾亮

（1.佛山科學(xué)技術(shù)學(xué)院數(shù)學(xué)與大數(shù)據(jù)學(xué)院，廣東佛山528000；2.廣東理工學(xué)院基礎(chǔ)教學(xué)部，廣東肇慶526100）

非等間距GM(1，1)模型的性質(zhì)研究

何敏藩1，曾亮2

（1.佛山科學(xué)技術(shù)學(xué)院數(shù)學(xué)與大數(shù)據(jù)學(xué)院，廣東佛山528000；2.廣東理工學(xué)院基礎(chǔ)教學(xué)部，廣東肇慶526100）

在現(xiàn)有非等間距GM(1，1)模型研究的基礎(chǔ)上，給出了模型的幾個(gè)重要性質(zhì)，為模型的應(yīng)用奠定了基礎(chǔ).關(guān)鍵詞：灰色系統(tǒng)；非等間距；GM(1，1)模型

自灰色系統(tǒng)理論提出以來，灰色預(yù)測(cè)模型在眾多領(lǐng)域中得到廣泛應(yīng)用.GM(1，1)模型是灰色預(yù)測(cè)模型中最主要和最常用的模型之一，它主要應(yīng)用于等間距數(shù)據(jù)序列的預(yù)測(cè).由于在實(shí)際工程中存在著大量的非等間距數(shù)據(jù)序列，并且需要對(duì)其做預(yù)測(cè)分析，所以建立非等間距GM(1，1)模型具有重要的意義.現(xiàn)已有部分學(xué)者針對(duì)非等間距序列構(gòu)建非等間距的GM(1，1)模型，取得了一些成果.從建模的方式上來看，主要分為兩種：第一種方式是通過在非等間距序列中分段線性插值，計(jì)算插值數(shù)據(jù)后得到等間距序列再建立GM(1，1)模型［1］；第二種方式是在對(duì)原始數(shù)據(jù)序列進(jìn)行一階累加生成時(shí)，將序列的間距作為乘子，然后按照非等間距方式建立GM(1，1)模型［2］.其中第二種方式建立的非等間距GM(1，1)模型近年來應(yīng)用較為廣泛［3-4］，對(duì)其改進(jìn)研究已成為研究的熱點(diǎn)［5-7］.

本文在文獻(xiàn)［2］提出的非等間距GM(1，1)模型的基礎(chǔ)上，深入研究時(shí)間序列和原始數(shù)據(jù)序列的變換對(duì)模型精度的影響，得到了3個(gè)重要性質(zhì)，為非等間距GM(1，1)模型的應(yīng)用奠定了理論基礎(chǔ).

1非等間距GM(1，1)模型

定義1設(shè)原始非等間距數(shù)據(jù)序列X(0)={x(0（)k1），x(0（)k2），…，x(0（)kn）}，其間距△ki=ki-ki-1≠const，i=2，3，…，n.若令△ki=1，則X(0)的一階累加生成序列X(1)={x(1（)k1），x(1（)k2），…，x(1（)kn）}，其中△kj，i=1，2，…，n.X(1)的緊鄰均值生成序列z(1)={z(1（)k2），z(1（)k3），…，z(1（)kn）}，其中z(1（)k）i=0.5（x(1（)k）i+x(1（)ki-1）），i=1，2，…，n.

定義2設(shè)X(0)，X(1)，Z(1)如定義1所述，則稱：為非等間距GM(1，1)模型.其白化微分方程為：

定理1設(shè)X(0)，X(1)，Z(1)如定義1所述，令：

則灰色微分方程x(0)（ki）+az(1)（ki）=u中的辨識(shí)參數(shù)a，u的最小二乘估計(jì)值滿足：

證明略.

證由于：

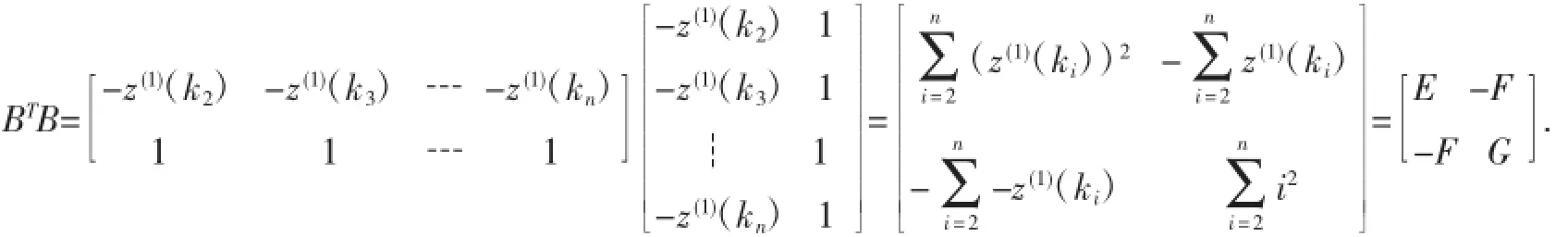
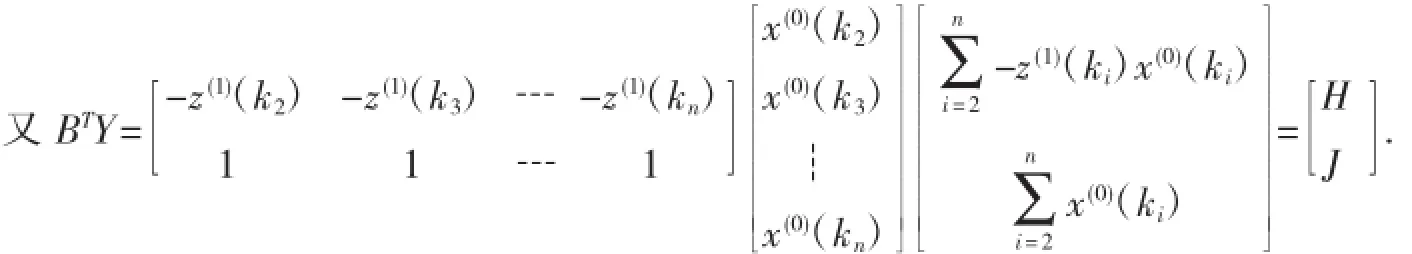
因此，由定理1可得：

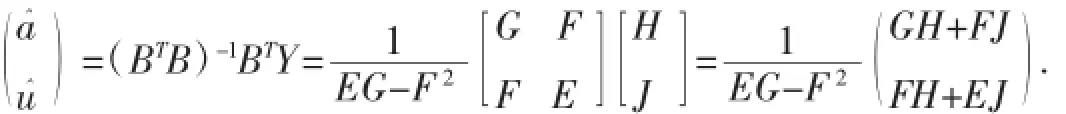
定理2設(shè)a^，u^滿足定理1所述條件，若規(guī)定t=k1時(shí)，x^(1)（k1）=x(1)（k1），則灰色微分方程x(0)（ki）+az(1)（ki）=u的時(shí)間響應(yīng)函數(shù)為：

還原值為：

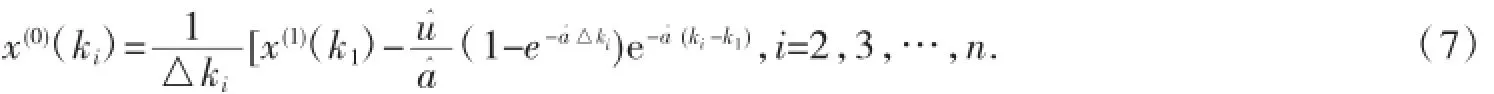
證明略.

3非等間距GM(1，1)模型的性質(zhì)

性質(zhì)1（時(shí)間序列線性變換無關(guān)性）設(shè)X(0)，X(1)，Z(1)如定義1所述，若對(duì)時(shí)間序列k={k1，k2，…，kn}做線性變換k~=mk+d（m，d為常數(shù)）后重新建立模型，則原始序列的模擬值不變，模型的平均模擬相對(duì)誤差也不變.

證記k~=mk+d={k~1，k~2，…，k~n}，顯然x(0)（k~i）=x(0)（ki），i=1，2，…，n.則間距△k~i=k~i-k~i-1=（mki+d）-（mki-1+d）=m（ki+ki-1）=m△ki，i=2，3，…，n.線性變換后X(0)的一階累加生成序列X軒(1)={x(1)（k~1），x(1)（k~2），…，x(1)（k~n）}，其中：

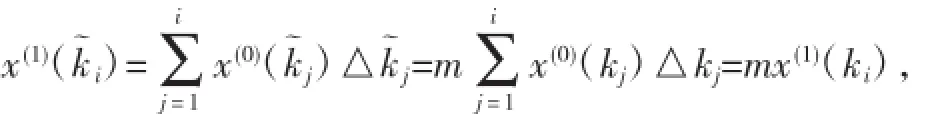
在區(qū)間[k~i-1，k~i]上對(duì)微分方程

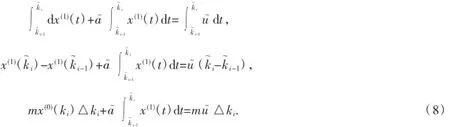
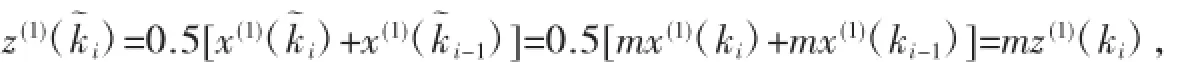
現(xiàn)用z(1)（k~i）△k~i近似代替的值，于是式（8）為：

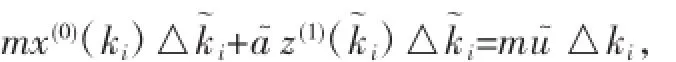
即：

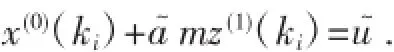
，則由定理1和推論可得a～，u～的最小二乘估計(jì)值為：

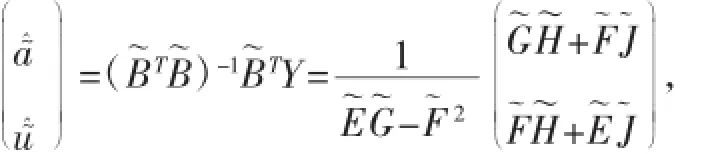
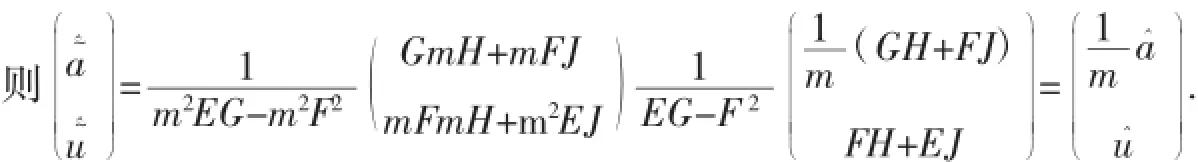
依此參數(shù)建立模型，由定理2可得還原值：

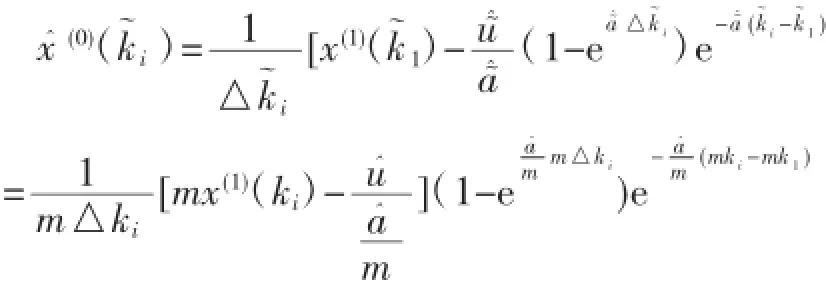
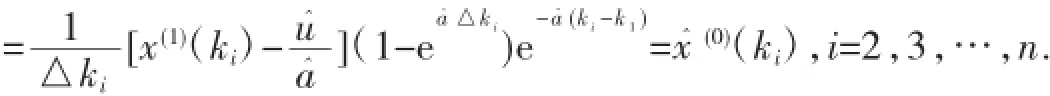
即原始序列模擬值不變，故平均模擬相對(duì)誤差也不改變.

性質(zhì)2（原始數(shù)據(jù)序列數(shù)乘變換無關(guān)性）設(shè)模型的原始數(shù)據(jù)序列為X(0)={x(0)（k1），x(0)（k2），…，x(0)（kn）}，若對(duì)數(shù)據(jù)序列做數(shù)乘變換X軒(0)=mX(0)（m為常數(shù)）后重新建立模型，模型的平均模擬相對(duì)誤差不改變.

證由X軒(0)=mX(0)，得x～(0)（ki）=mx(0)（ki），i=2，3，…，n.于是（ki），i=2，3，…，n.在區(qū)間[ki-1，ki]上對(duì)微分方程

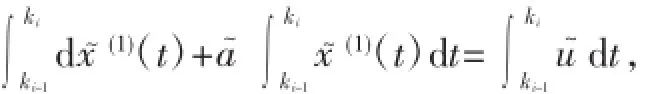
即：

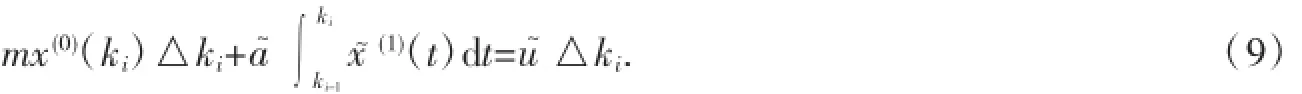
令X軒(1)的緊鄰均值生成序列Z~(1)={z～(1)（k2），z～(1)（k3），…，z～(1)（kn）}，其中z～(1)（ki）=0.5（x～(1)（ki）+x～(1)（ki-1）），i=2，3，…，n.于是可得：

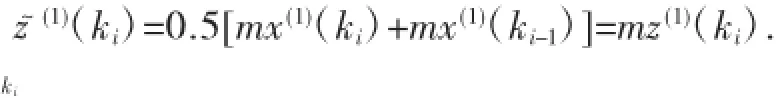
現(xiàn)用z～(1)（ki）△ki近似代替的值，于是式（9）為：

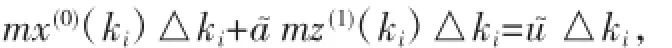
即：

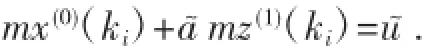
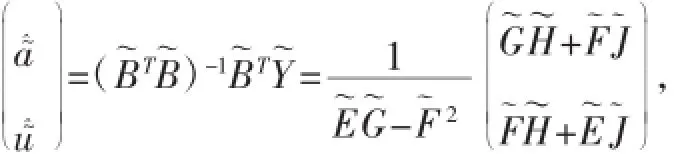
依此參數(shù)建立模型，由定理2可得還原值：

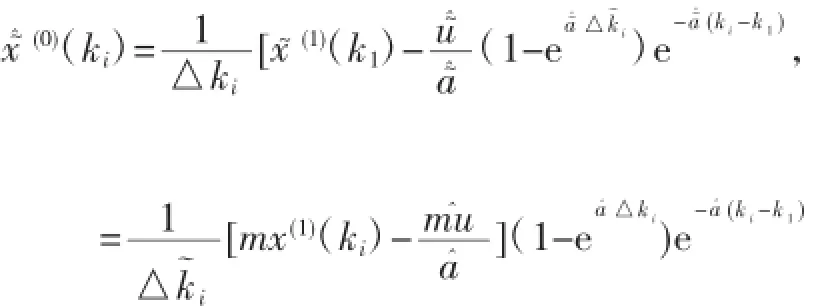
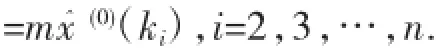
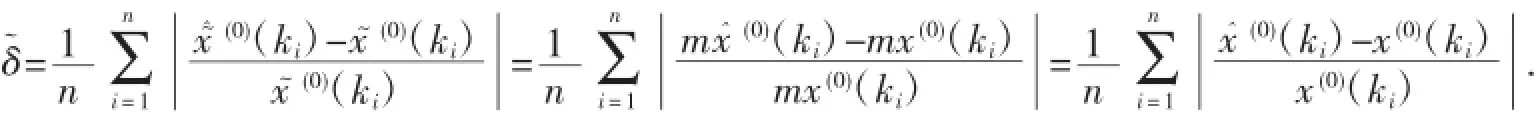
故平均模擬相對(duì)誤差：由此可見，模型的平均模擬相對(duì)誤差不改變.

性質(zhì)3（原始數(shù)據(jù)序列平移變換相關(guān)性）設(shè)模型的原始數(shù)據(jù)序列為X(0)={x(0)（k1），x(0)（k2），…，x(0)（kn）}，若對(duì)數(shù)據(jù)序列做平移變換X軒(0)=X(0)+d（d為常數(shù)）后重新建立模型，模型的平均模擬相對(duì)誤差發(fā)生改變.

證由X軒(0)=X(0)+d可得x～(0)（ki）=x(0)（ki）+d，i=1，2，…，n.于是：在區(qū)間[ki-1，ki]上對(duì)微分方程dx～1)（t）d

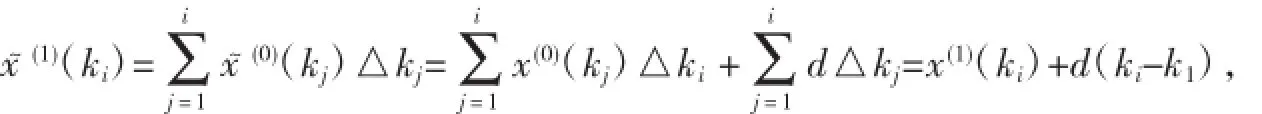
t+a～x～(1)（t）=u～積分，得：

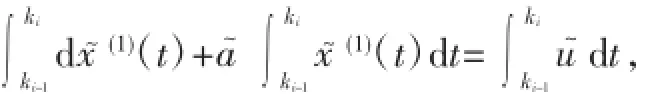
即：

即：

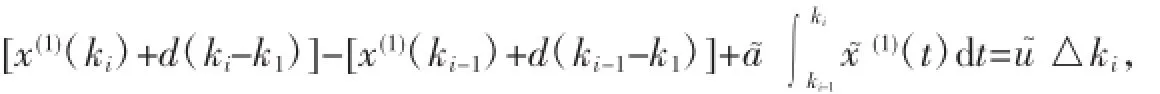
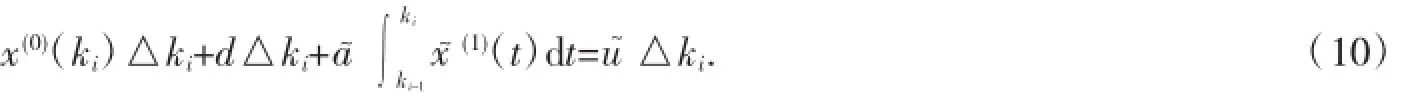
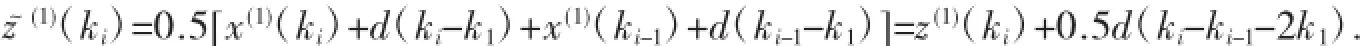
現(xiàn)用z～(1)（ki）△ki近似代替的值，于是式（10）為：

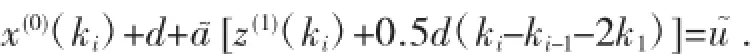
值為：

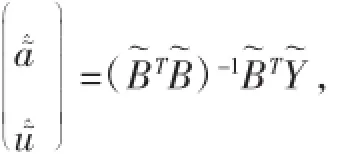
由于B軒式比較復(fù)雜，與d和時(shí)間序列有關(guān)，故所得a^～，u^~與原a^，u^并無固定的線性關(guān)系，從而x^～(0)（ki）=x^(0)（ki）+d一般不成立，即模型的平均模擬相對(duì)誤差一般發(fā)生改變.

3結(jié)語

本文在文獻(xiàn)［2］的基礎(chǔ)上，提出了關(guān)于非等間距GM(1，1)模型的3個(gè)性質(zhì).性質(zhì)1表明了在選取初始時(shí)間序列時(shí)可具靈活性；當(dāng)原始數(shù)據(jù)序列的數(shù)據(jù)比較大且樣本比較多時(shí)，易造成矩陣B病態(tài)，預(yù)測(cè)效果不理想，性質(zhì)2表明了可以通過數(shù)乘變換解決此問題.性質(zhì)3表明對(duì)原始數(shù)據(jù)序列的平移變換能改變模型的模擬預(yù)測(cè)精度，為實(shí)際應(yīng)用提供了一種優(yōu)化方法，即通過調(diào)整平移量，可使模型的精度達(dá)到最優(yōu).

［1］傅立.灰色系統(tǒng)理論及其應(yīng)用[M].北京：科技文獻(xiàn)出版社，1992.

［2］王鐘羨，吳春篤，史雪榮.非等間距序列的灰色模型[J].數(shù)學(xué)的實(shí)踐與認(rèn)識(shí)，2003，33(10)：16-20.

［3］吳邦彬，陳蘭，葛萃.改進(jìn)的非等間距GM(1，1)模型在大壩沉降分析中的應(yīng)用[J].水電能源科學(xué)，2012，30(6)：95-97.

［4］黃景銳，胡安焱，張煥楚，等.基于非等間距序列GM(1，1)模型的地下水溫度預(yù)測(cè)[J].水文地質(zhì)工程地質(zhì)，2013，40(1)：48-52.

［5］胡大紅.基于背景值與初始條件優(yōu)化的非等間距GM(1，1)模型[J].湖北文理學(xué)院學(xué)報(bào)，2016，37(11)：20-22.

［6］曾祥艷，曾玲.非等間距GM(1，1)模型的改進(jìn)與應(yīng)用[J].數(shù)學(xué)的實(shí)踐與認(rèn)識(shí)，2011，41(2)：90-95.

［7］熊萍萍，黨耀國(guó)，姚天祥.基于初始條件優(yōu)化的一種非等間距GM(1，1)建模方法[J].控制與決策，2015，30(11)：2097-2102.

Study on the Properties of Non-equidistant GM(1，1)Model

HE Min-fan1，ZENG Liang2
（1.School of Mathematics and Big Data，F(xiàn)oshan University，F(xiàn)oshan 528000，Guangdong，China;2.Department of Basic Courses，Guangdong Polytechnic College，Zhaoqing 526100，Guangdong，China）

In this paper，some important properties of the non-equidistant GM(1，1)model are given based on the existing research，which lays the foundation for the application of the model.

grey system;non-equidistant;GM(1，1)model

N941.5%

A%%%

1007-5348（2017）03-0015-06

（責(zé)任編輯：邵曉軍）

2017-01-02

何敏藩（1980-），男，江西上饒人，佛山科學(xué)技術(shù)學(xué)院數(shù)學(xué)與大數(shù)據(jù)學(xué)院講師，碩士；研究方向：數(shù)據(jù)挖掘和灰色系統(tǒng)等.