計及主動配電網轉供能力的可再生電源雙層優化規劃

劉 佳 徐 謙 程浩忠 蘭 洲 田 園

(1.上海交通大學電力傳輸與功率變換控制教育部重點實驗室 上海 200240 2.國網浙江省電力公司經濟技術研究院 杭州 310008)

?

計及主動配電網轉供能力的可再生電源雙層優化規劃

劉 佳1徐 謙2程浩忠1蘭 洲2田 園1

(1.上海交通大學電力傳輸與功率變換控制教育部重點實驗室 上海 200240 2.國網浙江省電力公司經濟技術研究院 杭州 310008)

在主動管理(AM)模式下，提出了一種考慮主動配電網轉供能力的可再生電源(RES)優化配置模型。以年綜合費最小為上層目標，每個場景的配電網運行費最小為下層目標，該模型計及了系統故障負荷的轉供和包括RES出力切除、RES功率因數調整、有載調壓變壓器分接頭調節和需求側管理在內的4種AM措施。考慮RES出力隨機性及負荷波動性，利用準蒙特卡羅模擬和奇異值分解生成風、光荷相關性樣本矩陣并采用模糊C-means聚類對場景進行縮減。應用動態小生境差分進化與原對偶內點算法相聯合的策略對模型加以求解。通過算例對比是否考慮AM措施和轉供能力下的三種情境仿真結果驗證了模型和方法的有效。

主動配電網 可再生電源 雙層優化規劃 主動管理 轉供能力

0 引言

近年來，作為發、輸電系統和終端用戶間的重要環節，配電網層面正大量接入以風電和光伏為代表的可再生電源(Renewable Energy Sources，RES)，經歷了從無源電網到有源電網的轉變。由于雙向潮流的出現，大大增加了配電網的不確定性和復雜性，給系統優化規劃及運行帶來了巨大的挑戰[1]。為了充分發揮RES在降低網損、改善線路潮流等方面的積極作用，需對其進行優化規劃。

在傳統的被動管理模式下，RES接入配電網后遵循“安裝即忘記”的原則，這樣不僅無法充分發揮RES的優勢，而且在一定程度上限制了RES的接入。隨著配電自動化和配電管理技術在中壓配電網中的廣泛應用，饋線所帶負荷信息可通過饋線終端裝置快速獲得[2]，遠程開關控制也將變得更加迅速[3]，使得配電網具有了可隨外部環境的變化實現負荷轉供和故障恢復的能力[4，5]及主動性特征[6]。主動配電網(Active Distribution Network，ADN)成為了配電網發展的一種新模式。一方面可對接入配電網的RES和其他設備進行主動管理(Active Management，AM)；另一方面可提高系統應對N-1故障能力和實現負荷有效轉移。ADN的出現對RES規劃問題提出了新的要求。

為提高ADN中的RES滲透容量，充分發揮ADN的資產效率，文獻[6-11]對AM模式下的RES規劃進行了相關研究。文獻[6]構造了一種計及可靠性成本、網絡損耗、購電費、網架投資成本在內的總費用最小的RES和ADN協調優化規劃模型。文獻[7]提出了一種通過識別ADN中薄弱節點的RES優先優化配置模型。文獻[8]考慮時變負荷和能源單價浮動，建立了計及RES接入后優化運行問題的長期RES動態規劃模型。文獻[9]以RES滲透容量最大為目標建立優化模型，并利用多時段的最優潮流算法對其加以求解。文獻[10]提出了一種AM模式下的分布式風電源雙層選址定容規劃模型，并將所得RES優化規劃方案與傳統機會約束規劃模型所得RES配置方法進行對比。文獻[11] 建立了一種間歇式分布式電源在ADN當中的機會約束優化規劃模型，并給出了結合蒙特卡羅模擬、遺傳算法和前推回代法的求解方法。

上述文獻是從不同角度出發，建立了N安全下的RES選址定容規劃模型并采用優化算法加以求解。但由于配電網中某個元件(如主變壓器、饋線等)故障也屬于不確定性范疇，而現有模型僅包含了負荷波動、間歇性RES出力等正常工況下的不確定因素，不確定性的內涵亟待完善。現有模型均未能充分計及ADN具有比傳統配電網更靈活的N-1后轉供能力，所得RES規劃方案也未必滿足相關要求。上述研究也未能對RES接入后的系統N-1轉供安全性給出定量評估。因此，有必要在RES優化配置階段就考慮ADN故障后轉供能力。

為彌補現有RES規劃方法的不足，本文建立了計及AM措施和ADN轉供能力的RES雙層優化配置模型。利用模糊C-means聚類法對采用準蒙特卡羅模擬(Quasi Monte Carlo Simulation，QMCS)和奇異值分解(Singular Value Decomposition，SVD)生成的風、光荷相關性樣本矩陣進行場景約簡。采用動態小生境差分進化算法(Dynamic Niche Differential Evolution Algorithm，DNDEA)聯合原對偶內點算法(Primal-Dual Interior Point Method，PDIPM)的混合方法求解規劃模型。最后，算例仿真結果表明文中模型所得RES優化配置方案提高了系統應對N-1故障的能力。

1 不確定因素建模

1.1 RES出力概率模型

風速通常采用雙參數Weibull分布來描述[12]。

(1)

式中，V為風電葉輪輪轂處的風速；r和c分別為形狀參數和尺度參數。

風電出力SWTG與風速V之間的關系可近似用分段函數[12]表示為

(2)

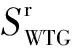
光照強度通常采用Beta分布[13]描述為

(3)

式中，I和Imax分別為光照強度及其最大值；α和β為Beta分布的兩個參數；Γ(·)為伽瑪函數。

光伏出力SPVG與光照強度I之間的關系可近似表示為[13]

(4)

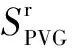
1.2 負荷不確定性模型

負荷采用正態分布的概率模型來描述[13]。

(5)

式中，SL、μp和σp分別為負荷的隨機量、期望和標準差。

1.3 配電網安全距離模型

配電網安全距離(DistributionSystemSecurityDistance，DSSD)是定量評估配電網N-1轉供安全裕度的一種新方法，它建立在配電網安全域理論上[14，15]。配電網安全域ΩDSSR是指在饋線N-1和主變壓器N-1轉供約束下，配電網能夠安全運行的所有工作點的集合[14]，因此，工作點在配電網安全域中的位置可以反映系統N-1轉供安全性，并利用其到配電網安全域各邊界的歐氏距離，即DSSD，來量化反映這一數據。基于交流潮流的DSSD模型可表述為

(6)

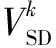
上述模型的具體計算方法已在文獻[15]中定義，在此不再贅述。當某工作點的安全距離為負值時，說明其不滿足N-1安全轉供，且安全距離越小，表征轉供不安全程度越高；當某工作點的安全距離為正值時，說明其滿足N-1安全轉供，且安全距離越大，表征轉供安全程度越高[14]。

2 相關樣本數據生成及簡化

2.1 QMCS和SVD生成相關性樣本

對于含風速、光照強度和負荷的3維隨機變量X=[X1,X2,X3]T，設其相關系數矩陣為[ρij]3×3，其中相關系數ρij定義為

(7)

式中，σi和σj分別為Xi和Xj的標準差；cov(Xi,Xj)為變量Xi、Xj的協方差。

本文采用基于Sobol序列的QMCS進行樣本采樣[16]。同時，考慮到相關系數矩陣非正定或非滿秩，其Cholesky分解不存在，而由于相關系數矩陣均為對稱陣，其SVD一直存在，因此，本文采用SVD對相關系數矩陣進行處理。QMCS聯合SVD能夠生成基于目標風、光荷相關系數矩陣[ρobj]3×3的相關樣本矩陣的理論依據可詳見文獻[17]。

應用QMCS和SVD產生相關性RES出力矩陣的具體過程如下:

1)設采樣規模為N，利用QMCS對風速、光照強度和負荷3個隨機輸入變量進行采樣，得到一個3×N階的初始樣本矩陣S0。

2)隨機生成一個3×N階的順序矩陣L，并按照式(7)計算L的相關系數矩陣ρL。

3)按照式(8)對ρL進行SVD并通過式(9)來消除由于隨機排列而產生的相關性。

(8)

(9)

式中，UL為酉矩陣；ΣL為由矩陣奇異值構成的對角矩陣。

4)按照式(10)對目標相關系數矩陣[ρobj]3×3進行SVD，并通過式(11)令Zu的相關系數矩陣與[ρobj]3×3近似相等。

(10)

(11)

5)更新初始樣本矩陣S0中的元素得到新的樣本矩陣Su。

2.2 模糊C-means聚類法簡化樣本數

為降低計算量和減少計算耗時，本文先采用模糊C-means聚類算法對2.1節得到的樣本矩陣Su進行約簡，從而減少計算最優潮流的次數而提高計算效率。模糊C-means聚類法[18，19]的核心求解思路是：從任意一個聚類中心開始，搜索目標函數值最小的點，并不斷更新聚類中心和調整樣本模糊隸屬度，最終確定樣本所屬大類。該方法對樣本數據的聚類中心及隸屬度的求取公式為

(12)

(13)

式中，xp為第p個樣本；μq為第q個聚類中心；δpq為xp屬于μq的隸屬度；ε為模糊度；Y為聚類數；N為樣本數。

統計落入每個類別的樣本數Ny(y=1,2,…,Y)，并計算每個場景發生的頻率py。

(14)

由大數定律可知，在滿足樣本數N足夠大的前提下，各場景發生的概率等于頻率py。

3 RES雙層優化配置模型

本文采用場景構建法將不確定因素(RES出力和負荷波動)對電網運行的作用效果轉換為一系列確定的場景進行處理。考慮有載調壓變壓器(On-LoadTapChanger，OLTC)抽頭調整、RES出力切除、RES功率因數調節以及需求側管理4種AM措施和N-1轉供約束，本文建立的RES優化配置模型在優化RES配置方案的同時，亦需優化ADN在每個場景下的運行方式，屬于典型的雙層規劃問題[20]。上層是以年綜合費最小為目標的RES優化配置問題，下層則是以每個場景的ADN運行費最小為目標的優化運行問題。上層規劃將RES配置方案傳遞給下層，下層規劃則在此基礎上對每個場景下的ADN進行優化運行模擬，并將計算結果傳遞給上層，從而指導上層規劃的決策。

3.1 上層規劃模型

具體數學表達式如下：

1)目標函數。

(15)

式中，CSUM、CI、COM,s、CAM,s、CP,s、CCE,s和CDSM,s分別為年綜合費、RES投資費、RES年運行維護費、RES年AM費、配電網向上級電網年購電費、碳排放成本和需求側管理成本；Ns為總場景數；下標中包含“s”的變量均表示場景s的值。

2)約束條件。

RES安裝容量上限約束為

(16)

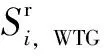
RES安裝容量離散性約束為

(17)

(18)

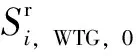
3.2 下層規劃模型

具體數學表達式如下：

1)目標函數。

minCOM,s+CAM,s+CP,s+CCE,s+CDSM,s

(19)

2)約束條件。

潮流方程約束為

(20)

(21)

式中，PGi,s和QGi,s分別為節點i發出的有功以及無功功率；PLi,s和QLi,s分別為節點i的有功以及無功需求；Ui,s和Uj,s分別為節點i和節點j的電壓；Gij為支路電導；Bij為支路電納；θij,s為節點i和節點j的電壓相角差；Nbus為配電網的節點數。

ADN轉供約束為

(22)

節點電壓約束為

(23)

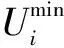
OLTC二次側電壓上、下限約束為

(24)

RES出力上、下限約束為

(25)

RES功率因數角上、下限約束為

(26)

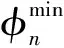
負荷中斷量上、下限約束為

(27)

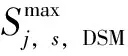
CI、COM,s、CAM,s、CP,s、CCE,s和CDSM,s為

(28)

(29)

(30)

CP,s=psρSgrid,s,PT

(31)

CCE,s=psηλSgrid,s,PT

(32)

(33)

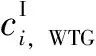
4 求解算法和步驟

分析上述RES雙層優化配置模型，其是含有多個決策變量的非線性混合整數雙層規劃問題。本文利用DNDEA聯合PDIPM的混合方法求解雙層規劃模型，該算法克服了差分進化算法在初期搜索速度快，后期易陷入局部最優點的缺點。

4.1DNDEA

差分進化算法(DifferentialEvolutionAlgorithm，DEA)[20]的基本過程可參見文獻[21]，這里不再贅述。本文綜合運用兩輪聯賽選擇，兩點交叉，單點均勻變異，交叉以及變異均采用不等概率，并引入精英保留策略。

與大多數群體智能算法一樣，DEA也存在容易陷入局部最優和收斂性較差等缺點。為了增加DEA對問題解空間的搜索性能，引入動態小生境機制[22，23]，得到DNDEA。動態小生境機制可促使群體內個體間協同合作，保持解的多樣性，提高全局搜索能力，使算法易于找出優化問題的所有局部最優解和全局最優解，適合多峰函數的優化[23]。

4.2 求解步驟

基于DNDEA聯合PDIPM的混合策略求解RES雙層優化配置模型的具體流程如圖1所示。

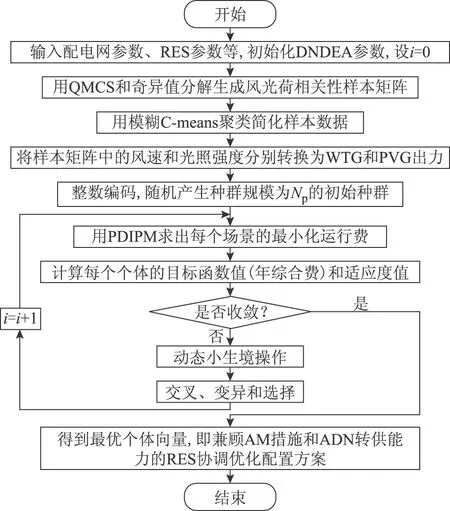
圖1 DNDEA聯合PDIPM求解優化模型流程Fig.1 Flow chart of solving optimal model based on DNDEA and PDIPM

5 算例分析

5.1 算例基本情況

算例配電網網架結構如圖2所示。算例共有3座33kV變電站、6臺主變壓器，20條11kV饋線和104個已有負荷節點，各節點負荷類型均相同且功率因數為0.85。算例中，各主變壓器及線路數據和已有負荷均值數據分別見表1和表2。負荷的標準差為均值的10%。

注：F1表示第1條饋線，以此類推。圖2 算例網絡Fig.2 Test system

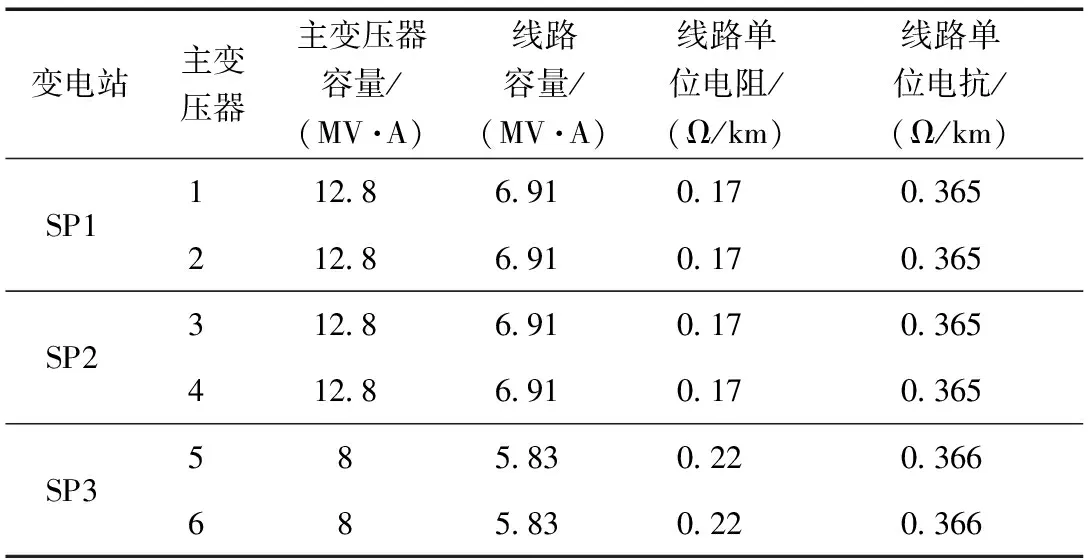
表1 各主變壓器及線路數據

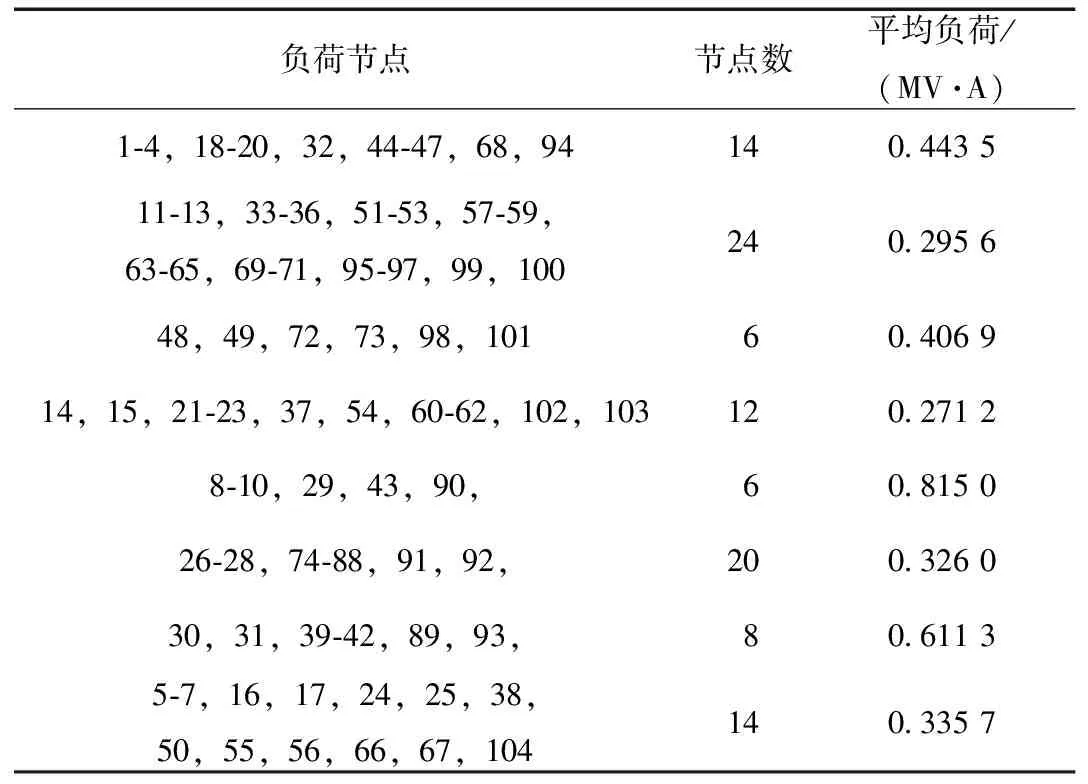
表2 已有負荷均值數據

一些規劃參數如下：RES的待選安裝節點為3、5、7、10、40、42、47和49，每個待選安裝節點的RES容量上限為5 MW，可中斷負荷點為4、6、9、41、43、46、48和50，中斷負荷恒功率因數被中斷。單臺風電的額定容量為0.5 MW，切入風速、額定風速和切出風速分別為3 m/s、13 m/s、20 m/s；風電的單位容量投資費為150 萬美元/MW，單位發電量的運行維護費和AM費分別為30美元/(MW·h)和22.5 美元/(MW·h)；風速服從r=2.15和c=8.32的Weibull分布。單個光伏的額定容量為0.5MW，額定光照強度為0.5kW/m2，最大光照強度為0.6kW/m2；光伏的單位容量投資費為175 萬美元/MW，單位發電量的運行維護費和AM費分別為40美元/(MW·h)和30 美元/(MW·h)；光照強度服從α=0.55和β=1.38的Beta分布。風電和光伏的使用年限均為20年，貼現率為0.06。節點電壓范圍為0.95(pu)～1.05(pu)。上級電網碳排放強度為639.2kg/(MW·h)，單位碳排放成本為10 美元/t，可中斷負荷點的補償單價為350 美元/(MW·h)。DNDEA的參數為：種群規模為50，最大迭代次數為50，交叉率和縮放因子均從0.9線性遞減到0.1。模糊C-means聚類數為50。

AM措施調節范圍參數如下：有載調壓變壓器二次側電壓的調節范圍為0.95(pu)～1.05(pu)，RES出力的削減率調節范圍為0～50%，RES的功率因數調節范圍為+0.98～-0.98，可中斷負荷點的中斷量范圍為0～全部。

本文分別選用年綜合費、安全距離變異系數作為評估RES配置方案經濟性、安全性的指標，權重系數均設為0.5。本文所有仿真的計算條件是：計算機CPU為i7-3 820，主頻為3.6GHz，內存為8GB，在Matlab2013a平臺上編制計算程序。

5.2 基于采樣數據的選址定容規劃結果

基于采樣數據，將本文所提出的模型用于算例研究，并采用DNDEA聯合PDIPM對規劃模型進行求解，得到考慮AM措施和ADN轉供能力的RES優化配置方案(記為方式1)見表3。作為對比，分別將規劃前、僅考慮ADN轉供能力(記為方式2)和僅考慮AM措施(記為方式3)的RES規劃方案和相應的各部分費用、RES滲透容量同樣列于表3當中，可以看出，是否考慮AM措施和ADN轉供能力將會改變RES的優化配置方案，從而影響規劃方案的經濟性以及RES滲透率。

此外，由表3還可以看出，同一方式下，各RES安裝節點配置的風電和光伏數量也不盡相同。這主要是因為系統各節點負荷功率、風電和光伏輸出功率在時空范圍內的概率分布存在差異性和互補性，能讓ADN在滿足安全運行的同時，盡可能多地接納RES，從而減少傳統電源的供電量，實現經濟效益和環境效益的綜合優化。

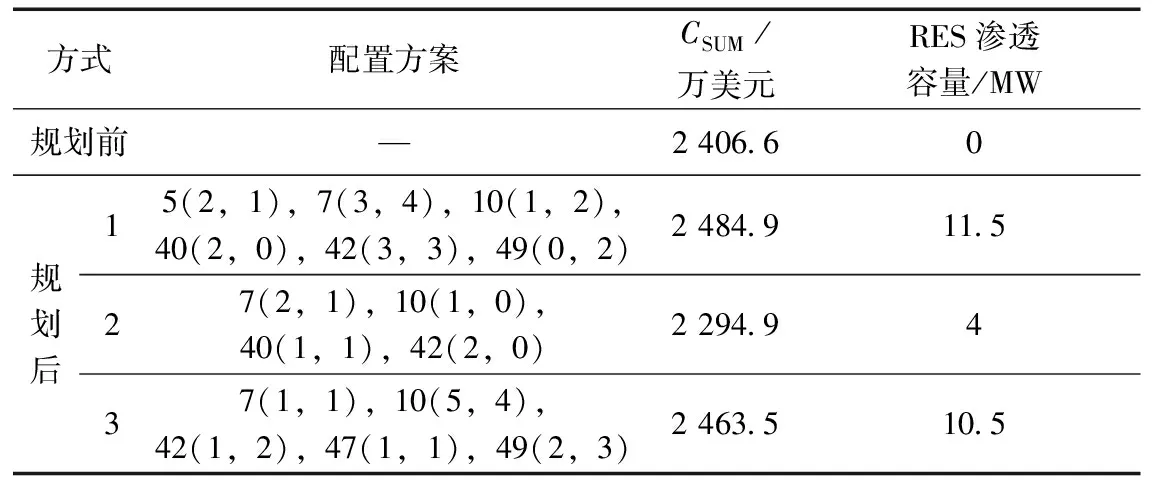
表3 不同方式下基于采樣數據的規劃結果

注：5(2，1)表示節點5安裝2臺風電，1個光伏，以此類推。

各方式所對應的各部分費用和ADN中各饋線的安全距離情況分別如圖3和圖4所示。

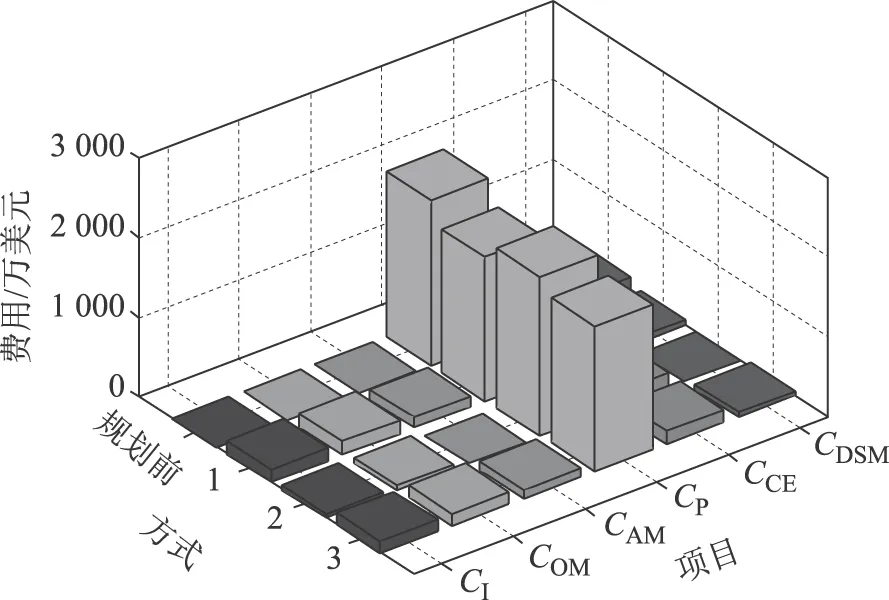
圖3 不同方式下基于采樣數據的各部分費用Fig.3 Costs under various modes based on sampling data

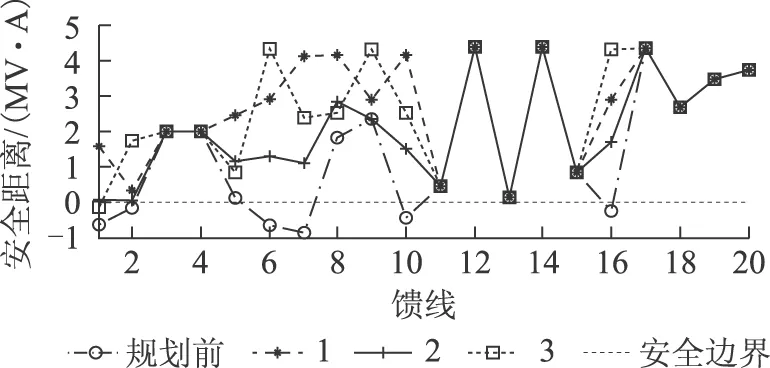
圖4 各饋線基于采樣數據的安全距離Fig.4 Security distance of feeders based on sampling data

由表3和圖4可以看出，從綜合提高系統經濟性和安全性的角度出發，方式1下的RES規劃方案較規劃前更優。解釋其原因如下：雖然方式1比規劃前的年綜合費用增加了78.3 萬美元，增幅達3.2%，但是，考慮到規劃前ADN中有6條饋線的安全距離均為負值且各條饋線的安全距離變異系數為1.25，而經方式1規劃后ADN中各條饋線的安全距離均為正值且各條饋線的安全距離變異系數為0.53，相較之下，方式1比規劃前的各條饋線的安全距離變異系數小了0.72，降幅達57.6%，兼顧系統經濟性和安全性，方式1更好。

5.3 計及AM對規劃結果的影響

為了說明AM對規劃結果的影響，將方式1和方式2的規劃結果進行對比分析。由表3可以看出，方式1的RES滲透容量為11.5 MW，而方式2的RES滲透容量僅為4 MW，說明AM措施可以增加RES的滲透容量，提高配電網的資產利用率。由圖3可以看出，方式1的碳排放成本和年購電費分別為162.81萬美元和1 797.90萬美元，而方式2的碳排放成本和年購電費分別為181.62萬美元和2 005.70萬美元，說明AM措施可減少傳統電源的發電量，達到減少碳排放的效果。

同時，由表3和圖4可以看出，從綜合提高系統經濟性和安全性的角度出發，方式1較方式2下的RES規劃方案更優。解釋其原因如下：雖然方式1比方式2的年綜合費用增加了190 萬美元，增幅達7.6%，但是，考慮到方式2的ADN中各條饋線的安全距離變異系數為0.72，而經方式1規劃后ADN中各條饋線的安全距離變異系數為0.53，相較之下，方式1比方式2的各條饋線的安全距離變異系數小了0.19，降幅達26.4%，兼顧系統經濟性和安全性，方式1更好。

5.4 計及ADN轉供能力對規劃結果的影響

為了研究計及ADN轉供能力對規劃結果的影響，將方式1和方式3的規劃結果進行對比分析。由表3和圖4可以看出，從綜合提高系統經濟性和安全性的角度出發，方式1較方式3下的RES規劃方案更優。解釋其原因如下：雖然方式1比方式3的年綜合費用增加了21.4 萬美元，增幅達0.9%，但是，考慮到方式3的ADN中有1條饋線的安全距離為負值且各條饋線的安全距離變異系數為0.61，而經方式1規劃后ADN中各條饋線的安全距離均為正值且各條饋線的安全距離變異系數為0.53，相較之下，方式1比方式3的各條饋線的安全距離變異系數小了0.08，降幅達13.1%，兼顧系統經濟性和安全性，方式1更好。

5.5 基于歷史觀測數據的規劃結果

為進一步論證規劃模型的有效性，基于風、光荷歷史觀測數據進行RES規劃。設該ADN所在區域的風速、光照強度和負荷的年變化曲線如圖5所示。其中，風速和光照強度的曲線是基于月平均氣象數據，借助HOMER軟件離散得到。離散后的全年氣象數據基本能夠反映該區域的天氣特征。利用模糊C-means方法對圖5中的時序風速、光照強度和負荷數據進行聚類。在此基礎上，用提出的混合求解策略對規劃模型進行求解，得到不同方式下的規劃結果見表4。圖6給出了各饋線的安全距離情況。

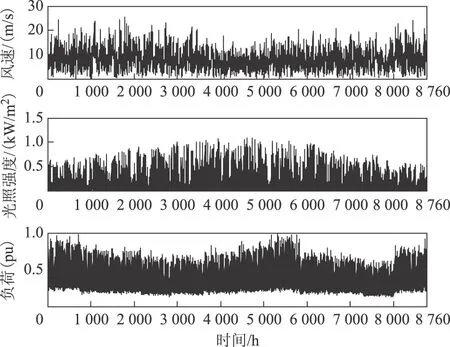
圖5 風速、光照強度和負荷的年變化曲線Fig.5 Annual wind speed，illumination intensity and load curve

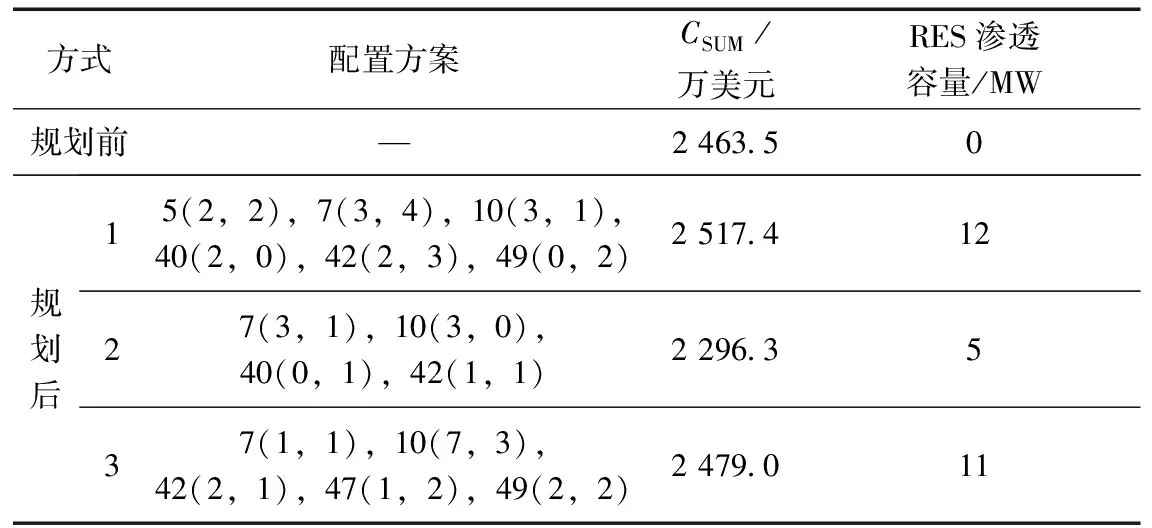
表4 不同方式下基于歷史觀測數據的規劃結果

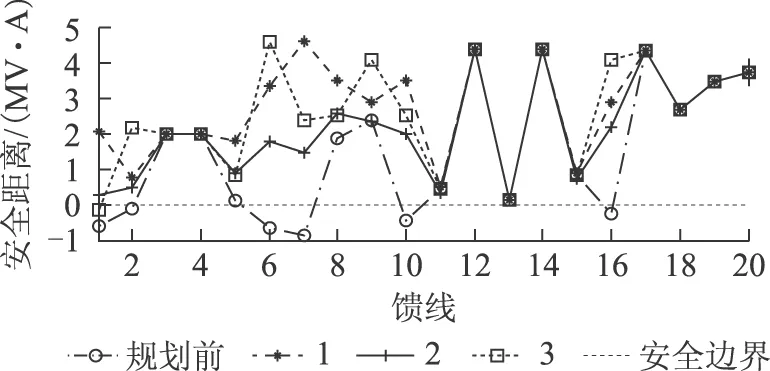
圖6 各饋線基于歷史觀測數據的安全距離Fig.6 Security distance of feeders based on historic data

由表3和表4可以看出，各方式下基于采樣數據和歷史觀測數據的RES優化配置方案均不相同。這主要是因為風、光荷在時空范圍內的概率分布存在差異性和互補性。

由表4和圖6可以看出，從綜合提高系統經濟性和安全性的角度出發，對比規劃前和方式1、2、3下的RES規劃方案，方式1最優。具體其原因可類比5.2節～5.4節中相關內容說明。

5.6 基于采樣數據的算法性能比較

分別采用遍歷法、K-means聚類法和模糊C-means聚類法計算方式1、2和3最優配置方案對應的年綜合費，得到的結果見表5。

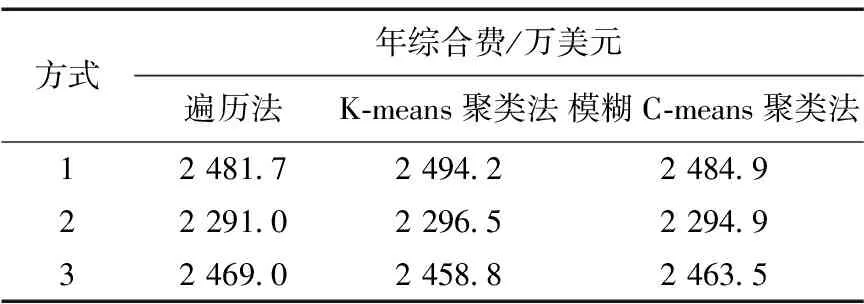
表5 三種算法性能對比

由表5中可以看出，對比K-means聚類法，運用模糊C-means聚類法約簡樣本所得到的計算結果與采用遍歷法得到的結果更加逼近，誤差更小，這表明：①運用模糊C-means聚類法對風速、光照強度和負荷樣本矩陣進行簡化的求解思路是正確有效的，在保證計算精度的前提下，提高了計算效率；②模糊C-means聚類法較K-means聚類法在保證樣本準確度上具有優越性。

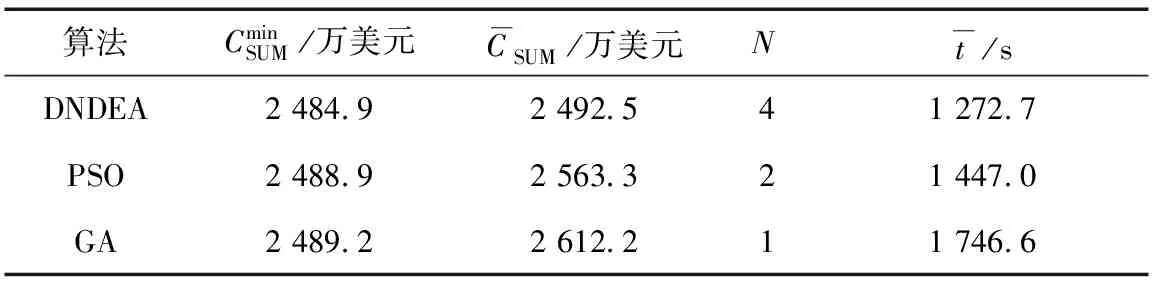
表6 各算法收斂特性對比

6 結論

本文考慮風、光荷間的相關性，分別以年綜合費最小和每個場景的配電網運行費最小作為上、下層優化目標，建立了計及AM措施和ADN轉供能力的RES雙層規劃模型。首先，利用模糊C-means聚類法對樣本數據進行約簡，然后運用DNDEA聯合PDIPM的混合方法求解雙層規劃模型，算例仿真結果表明：

1)通過RES規劃，有助于提升系統應對N-1故障的能力和實現故障負荷的有效轉供，使得ADN具有了更強的自愈性特征。

2)相對于僅考慮ADN轉供能力或僅考慮AM措施的RES規劃模型，從綜合提高配電網經濟性和安全性角度出發，本文規劃模型改善效果更明顯。

3)AM措施有助于提高ADN中RES的滲透容量，提高配電網的資產利用率，從而減少傳統電源的發電量，達到碳減排的目標。

4)RES的合理優化配置對于改善工作點在配電網安全域當中的位置和轉供安全裕度的大小具有積極的作用。

5)利用模糊C-means聚類法對樣本矩陣進行約簡，能夠在提高計算效率的同時，保證樣本數據的準確性。

[1] 張建華，曾博，張玉瑩，等.主動配電網規劃關鍵問題與研究展望[J].電工技術學報，2014，29(2)：13-23. Zhang Jianhua，Zeng Bo，Zhang Yuying，et al.Key issues and research prospects of active distribution network planning[J].Transactions of China Electrotechnical Society，2014，29(2)：13-23.

[2] Li Yujuan，Wang Fanrong.Implementation of smart grid software system based on configurable feeder terminal unit[C]//2012 IEEE Symposium on Electrical & Electronics Engineering，2012：277-280.

[3] De Groot R J W，Morren J，Slootweg J G.Smart integration of distribution automation applications[C]//2012 3rd IEEE PES International Conference and Exhibition on Innovative Smart Grid Technologies，2012：1-7.

[4] 廖懷慶，劉東，黃玉輝，等.考慮新能源發電與儲能裝置接入的智能電網轉供能力分析[J].中國電機工程學報，2012，32(16)：9-16. Liao Huaiqing，Liu Dong，Huang Yuhui，et al.Smart grid power transfer capability analysis considering integrated renewable energy resources and energy storage systems[J].Proceedings of the CSEE，2012，32(16)：9-16.

[5] 馬靜，馬偉，王增平.基于聯絡關系的主變故障負荷轉供方案[J].電力系統保護與控制，2014，42(19)：1-7. Ma Jing，Ma Wei，Wang Zengping.Power restoration scheme for main transformer fault based on the interconnection relationship[J].Power System Protection and Control，2014，42(19)：1-7.

[6] Martins V F，Borges C L T.Active distribution network integrated planning incorporating distributed generation and load response uncertainties[J].IEEE Transactions on Power Systems，2011，26(4)：2164-2172.

[7] Zhao Yuanyuan，An Yiran，Ai Qian.Research on size and location of distributed generation with vulnerable node identification in the active distribution network[J].IET Generation，Transmission & Distribution，2014，8(11)：1801-1809.

[8] Abapour S，Zare K，Mohammadi-Ivatloo B.Dynamic planning of distributed generation units in active distribution network[J].IET Generation，Transmission & Distribution，2015，9(12)：1455-1463.

[9] Siano P，Chen P，Chen Z，et al.Evaluating maximum wind energy exploitation in active distribution networks[J].IET Generation，Transmission & Distribution，2010，4(5)：598-608.

[10]Zhang Jietan，Fan Hong，Tang Wenting，et al.Planning for distributed wind generation under active management mode[J].International Journal of Electrical Power & Energy Systems，2013，47(6)：140-146.

[11]馬瑞，金艷，劉鳴春.基于機會約束規劃的主動配電網分布式風光雙層優化配置[J].電工技術學報，2016，31(3)：145-154. Ma Rui，Jin Yan，Liu Mingchun.Bi-level optimal configuration of distributed wind and photovoltaic generations in active distribution network based on chance constrained programming[J].Transactions of China Electrotechnical Society，2016，31(3)：145-154.

[12]鄧威，李欣然，李培強，等.基于互補性的間歇性分布式電源在配網中的優化配置[J].電工技術學報，2013，28(6)：216-225. Deng Wei，Li Xinran，Li Peiqiang，et al.Optimal allocation of intermittent distributed generation considering complementarity in distributed network[J].Transactions of China Electrotechnical Society，2013，28(6)：216-225.

[13]Zhang Shenxi，Cheng Haozhong，Zhang Libo，et al.Probabilistic evaluation of available load supply capability for distribution system[J].IEEE Transactions on Power Systems，2013，28(3)：3215-3225.

[14]Xiao J，Gu W，Wang C，et al.Distribution system security region：definition，model and security assessment[J].IET Generation，Transmission & Distribution，2012，6(10)：1029-1035.

[15]Xiao Jun，Zu Guoqiang，Gong Xiaoxu，et al.Model and topological characteristics of power distribution system security region[J].Journal of Applied Mathematics，2014(6)：1-13.

[16]Singhee A，Rutenbar R.Why quasi-Monte Carlo is better than Monte Carlo or Latin hypercube sampling for statistical circuit analysis[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems，2010，29(11)：1763-1776.

[17]Iman R L，Conover W J.A distribution-free approach to inducing rank correlation among input variables[J].Communications in Statistics-Simulation and Computation，1982，11(3)：311-334.

[18]李贏，舒乃秋.基于模糊聚類和完全二叉樹支持向量機的變壓器故障診斷[J].電工技術學報，2016，31(4)：64-70. Li Ying，Shu Naiqiu.Transformer fault diagnosis based on fuzzy clustering and complete binary tree support vector machine[J].Transactions of China Electrotechnical Society，2016，31(4)：64-70.

[19]Murata R，Endo Y，Haruyama H，et al.On fuzzy C-means for data with tolerance[J].Advanced Computational Intelligence and Intelligent Informatics，2006，10(5)：673-681.

[20]藤春賢，李智慧.二層規劃的理論與應用[M].北京：科學出版社，2002.

[21]Storn R，Price K.Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization，1997，11(4)：341-359.

[22]盧揚，吳俊勇，郝亮亮.基于改進MOBPSO算法的含分布式電源的多目標配電網重構[J].電力系統保護與控制，2016，44(7)：62-68. Lu Yang，Wu Junyong，Hao Liangliang.Multi-objective distribution network reconfiguration with distributed generations based on improved MOBPSO algorithm[J].Power System Protection and Control，2016，44(7)：62-68.

[23]Della Cioppa A，De Stefano C，Marcelli A.Where are the niches? Dynamic fitness sharing[J].IEEE Transactions on Evolutionary Computation，2007，11(4)：453-465.

(編輯 赫蕾)

Bi-Level Optimal Renewable Energy Sources Planning Considering Active Distribution Network Power Transfer Capability

LiuJia1XuQian2ChengHaozhong1LanZhou2TianYuan1

(1.Key Laboratory of Control of Power Transmission and Conversion Ministry of Education Shanghai Jiao Tong University Shanghai 200240 China 2.State Grid Zhejiang Electric Power Corporation Economic Research Institute Hangzhou 310008 China)

Under the active management(AM)mode，an optimal Renewable Energy Sources(RES)allocation model is proposed.The model takes the minimum annual total cost and the minimum scenario-based distribution network operation cost as the objectives of upper and lower level，respectively.The power transfer of system fault load and four AM schemes are considered in the optimization formulation.The AM schemes including RES output power resection，RES power factor adjustment，on-load regulating transformer tap adjustment and in-side management measures.Given the randomness of RES output power and load fluctuation，the correlation between wind and light load sample matrix is generated by quasi Monte Carlo simulation and singular value decomposition and then simplified by fuzzy C-means clustering.A hybrid strategy combining dynamic niche differential evolution algorithm and primal-dual interior point method is applied to the model.The compared simulation results demonstrate the effectiveness of the proposed model and method.

Active distribution network，renewable energy sources，bi-level optimal programming，active management，power transfer capability

國家重點研發計劃(2016YFB0900102)和國家電網公司科技項目(5211JY16004)資助。

2016-05-10 改稿日期2016-07-12

TM715

劉 佳 男，1991年生，博士研究生，研究方向為電力系統優化、規劃、運行。

E-mail：liujia911011@126.com(通信作者)

徐 謙 男，1963年生，碩士，高級工程師，研究方向為電力系統規劃和運行。

E-mail：xuqian1963@sina.com