特高壓交直流混聯條件下四川電網低頻振蕩模態分析

張 航，王曉茹

(西南交通大學電氣工程學院，四川 成都 610031)

特高壓交直流混聯條件下四川電網低頻振蕩模態分析

張 航，王曉茹

(西南交通大學電氣工程學院，四川 成都 610031)

以2017年“三華”電網模型為基礎，研究了含特高壓輸電線路的四川電網內部的低頻振蕩模式。對目前已有低頻振蕩機理進行了總結。通過對不同典型運行方式的分析，指出了含特高壓輸電線路的四川電網存在的幾種振蕩模式，并論證了電力系統穩定器(PSS)對抑制該振蕩頻率的重要性；開展了時域、頻域的對比分析及驗證，提出時域仿真分析中進行參數辨識的典型經驗。最后，對下一步開展低頻振蕩研究工作的重點和方向進行了展望。

特高壓；低頻振蕩；強迫振蕩；電力系統穩定器

0 引 言

近年來，隨著電力系統規模不斷擴大，特高壓輸電線路的增長以及大容量機組、快速勵磁裝置的投運，互聯電網運行愈接近極限臨界點，振蕩失穩問題日漸嚴重，最常見的就是低頻振蕩。低頻振蕩是電力系統穩定運行中的重要議題，快速并準確地辨識低頻振蕩模式對電網的低頻振蕩分析和控制有著極為重要的意義[1]。中國西部能源基地距離東部重負荷中心較遠，外送電力規模很大，發展直流輸電技術是大勢所趨。在中國已經形成多直流送出和多直流饋入電網，相應的交直流網架系統正逐步建成，其對混聯電網的運行和控制也提出了更高的要求。2015年四川通過特高壓輸電工程外送清潔水電達到103 841 Gwh，減少火電原煤消耗4 000多萬噸，減少二氧化碳排放1.5億噸。可以預見，隨著經濟社會發展以及技術的提升，未來十年隨著西南電網以及西部電網的建設，四川將迎來特高壓輸電技術大跨越發展時期，而特高壓工程使得四川電網和外網之間的電氣聯系更加緊密。在此背景下，結合四川電網實際工程研究特高壓交直流系統下的小擾動穩定性，具有極其重要的工程價值和現實意義。

基于含特高壓輸電線路的四川電網仿真模型，開展低頻振蕩專題研究；分析特高壓輸電工程投產后四川主要存在的低頻振蕩模式，并對比基于模型和量測數據的辨識結果，結合當前實際工程問題對低頻振蕩抑制措施提出了建議。

1 低頻振蕩機理

目前，低頻振蕩產生機理主要有3個方面：負阻尼機理、強迫振蕩機理和混沌理論。

負阻尼機理是由F. P. Demello于1969年提出來的[2]，該理論認為發電機阻尼轉矩不足導致了小擾動功角失穩，原因在于高倍率的勵磁放大系統導致系統阻尼下降，系統對某些固有頻率的振蕩表現出負阻尼特性，抵消了系統固有的正阻尼，使得系統的總阻尼很小或者為負，這樣一旦出現擾動，就會引起轉子增幅振蕩或者振蕩不收斂。當遠距離輸電線路潮流較重時有可能出現阻尼較低甚至為負的低頻振蕩，若系統中大量使用快速勵磁系統，則系統的阻尼問題更為嚴重。電力系統受到擾動后會出現低頻振蕩現象，而當系統阻尼較低時低頻振蕩衰減較慢，振蕩持續時間較長，當系統阻尼為負時振蕩幅值不斷增大，最終引起系統失穩解列。負阻尼機理是目前發展最為完善的低頻振蕩機理，已成為解析低頻振蕩現象和設計電力系統穩定器(power system stabilizer, PSS)的主要理論依據。

強迫振蕩著重關注于周期性負荷波動或振蕩調節的作用。當發電機受到的周期性擾動頻率接近系統固有振蕩頻率時，在該頻率下便會引起系統諧振，導致大幅度的功率振蕩[3]。強迫振蕩具有當擾動源存在時振蕩迅速起振、當擾動源消失時振蕩迅速消失和起振后保持等幅同步振蕩等特點。文獻[4]通過仿真算例分別簡要分析了同步力矩系數、阻尼轉矩系數、發電機組的慣性時間常數和擾動量幅值對系統共振特性的影響程度，同時歸納出了振蕩特性。文獻[5]基于能量角度分析了電力系統在發生共振機理低頻振蕩過程中，內、外能量的變化關系和特征。文獻[6]對電力系統中原動機功率和負荷的持續周期性小擾動造成電網強迫功率振蕩進行了分析，闡述了這兩種擾動源的不同性質。在強迫振蕩的研究中，強迫振蕩源定位是關鍵，文獻[7-8]分別運用基于能量和波形相似度的方法進行強迫振蕩源定位。

混沌理論認為電力系統參數或擾動在一定范圍內變化時，由于電力系統非線性的影響使得系統參數間相互作用，導致系統穩定結構發生變化，進而產生振蕩，如非周期性、似乎無規則的突發性機電振蕩。該理論與成熟的線性系統理論相去甚遠，受到數學工具的限制，仍停留在理論探索階段[9]。

負阻尼機理、混沌機理都與系統本身的固有結構和參數有關，強迫振蕩機理與擾動信號有關。除了以上3種理論，還有其他原因解釋低頻振蕩現象，例如交直流系統間的相互作用、電網鏈式分布、區域間功率不平衡[10]等。值得一提的是，電力系統是一個復雜的動態系統，不同機理的低頻振蕩可能同時發生；不同模式的振蕩彼此之間有時候會相互作用，這時需考慮系統結構和運行方式對低頻振蕩模式的影響，準確辨識出低頻振蕩的主導模式。

2 研究對象及研究方法

采用四川電網2017年網架，計算中考慮豐大、枯大這兩種典型方式。主要機組的發電機模型多采用考慮阻尼繞組的次暫態模型。當前四川電網接入500kV電網的主力機組主要采用自并勵靜止勵磁系統，勵磁系統均配置了電力系統穩定器(PSS)模塊，且通過實測建立了勵磁系統及PSS模型。計算采用的負荷模型為純靜態負荷模型。

當前電網低頻振蕩分析方法主要可分為頻域、時域兩大類，依據研究對象和目標的不同以及各種方法的不同特點分別用于不同場合。其中，隱式重啟動Arnorldi算法屬于典型的特征值分析法，在大規模電力系統實際分析中存在一定優勢，并已被集成在PSASP程序中，下面將采用該方法開展研究。

3 計算結果及分析

3.1 豐大方式下四川電網主要振蕩模式

2017年豐大方式下，采用小擾動穩定分析程序(PSD-SSAP)隱式重啟動Arnoldi算法得出四川電網內部共6個機電振蕩模式。其對應的特征值如表1所示。

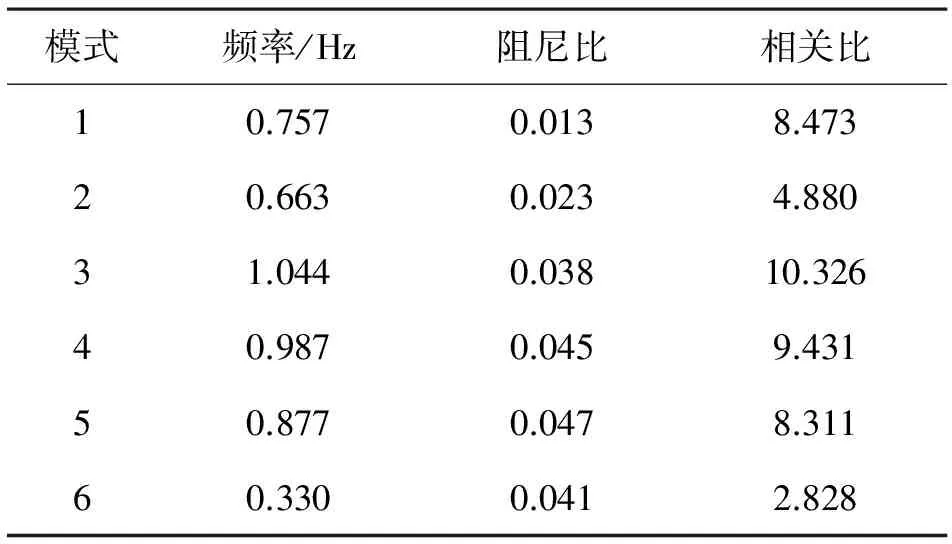
表1 豐大方式下存在的低頻振蕩模式信息

從表1可以看出，模式2、模式6的阻尼比較小，屬于弱阻尼模式。下面將分別對這6個振蕩模式進行詳細分析，分析得出每個振蕩模式下參與因子較高的機組，并對阻尼比為負或者阻尼比較小的振蕩模式通過對相關機組加裝PSS來提高系統阻尼。

1) 康定和溪洛渡之間的振蕩

2017年豐大方式，存在特征值為-0.064+j4.759，頻率為0.757 Hz，阻尼比為0.013的振蕩模式，該模式機電回路相關比為8.473，主要表現為丹巴、康定機組對溪洛渡機組的振蕩，機組模態分布圖如圖1所示。

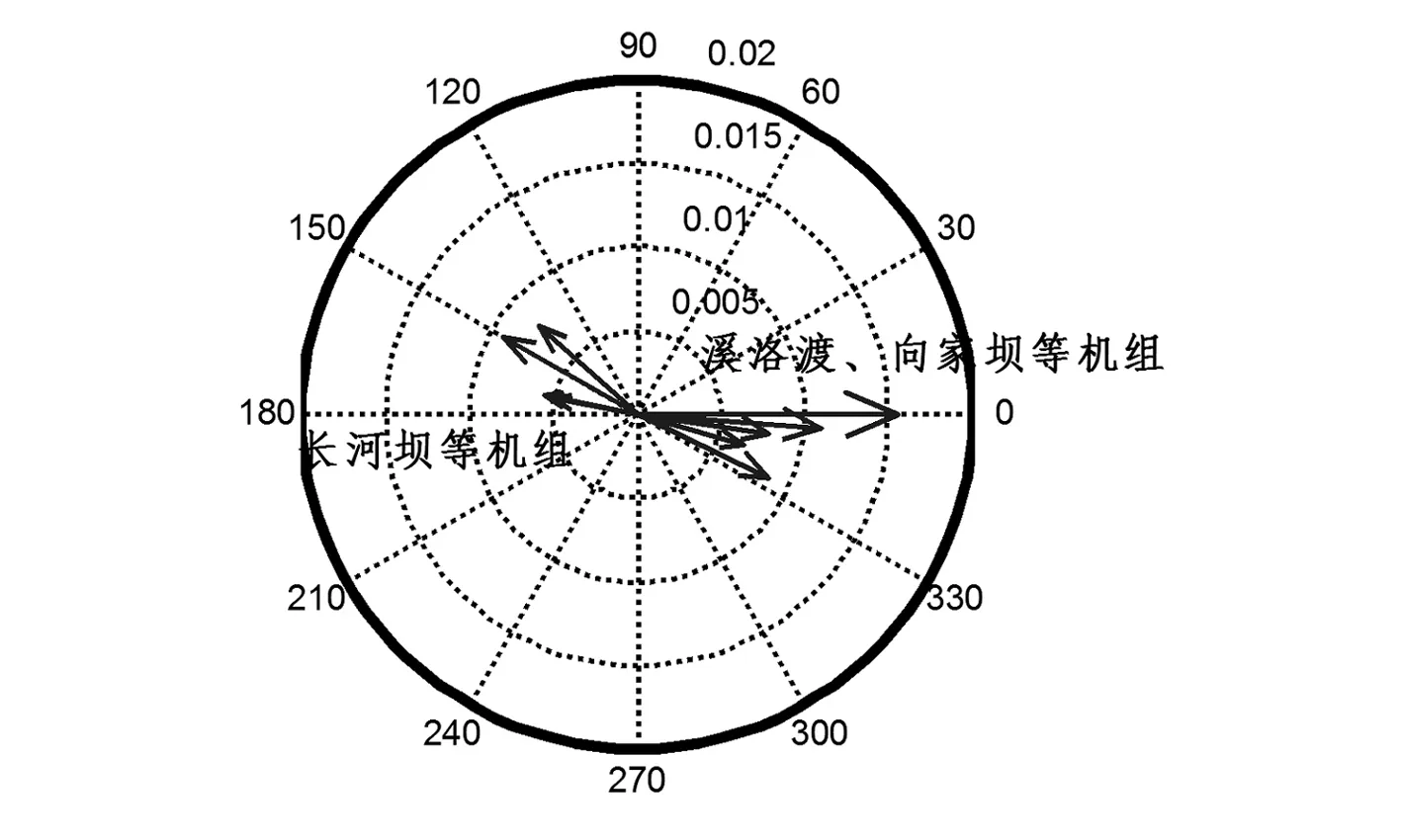
圖1 康定對溪洛渡的振蕩模態

通過對溪洛渡左、長河壩機組加裝PSS后，向家壩左—長河壩間的振蕩模式的阻尼比有所增加，振蕩頻率變為0.737 7 Hz，阻尼比為0.070 0，說明溪洛渡機組PSS的投入對該振蕩模式的抑制效果十分明顯。

2) 丹巴對木里模式

該振蕩模式頻率為0.663 Hz，阻尼比為0.023，主要表現為丹巴、康定機組相對鄉城、木里機組的振蕩，機組模態分布圖如圖2所示。

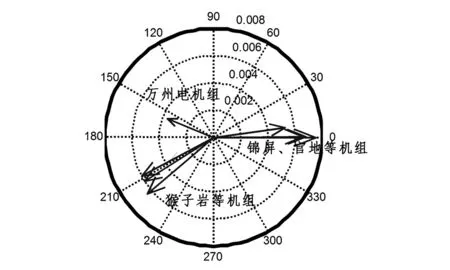
圖2 丹巴對木里的振蕩模態

通過對猴子巖、長河壩機組加裝PSS后，色玉—古瓦間的振蕩模式的阻尼比有所增加，振蕩頻率變為0.647 1 Hz，阻尼比為0.038 7。

3) 向家壩機組對鄉城機組模式

該振蕩模式的頻率為1.044 Hz，阻尼比為0.038，主要表現為向家壩、新平、方山和鄉城地區間的振蕩，機組模態分布圖如圖3所示。

4)錦屏對鄉城模式

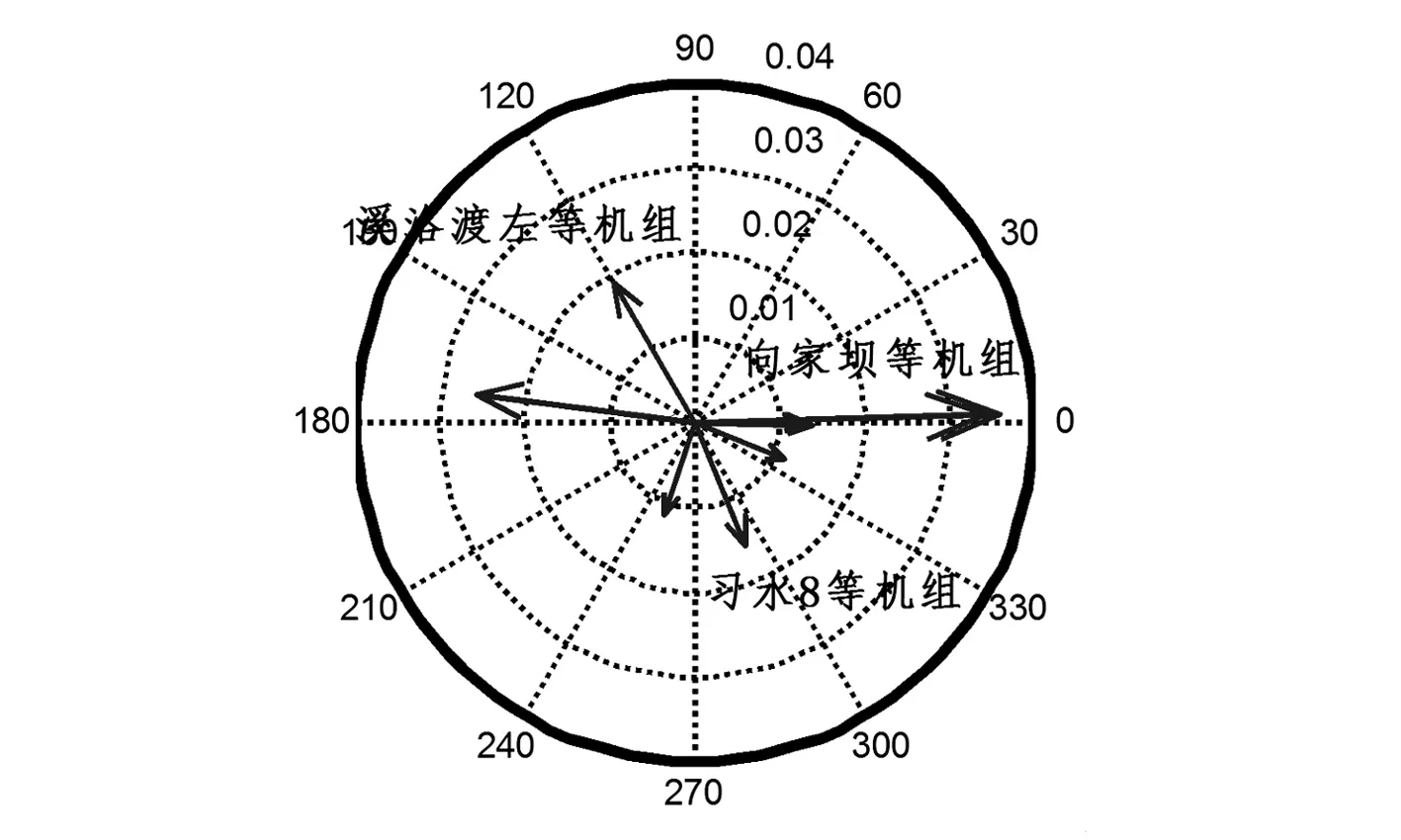
圖3 向家壩對鄉城的振蕩模態

該振蕩模式的頻率為0.987 Hz，阻尼比為0.045，主要表現為錦屏和鄉城、木里間的振蕩，機組振蕩模態圖如圖4所示。

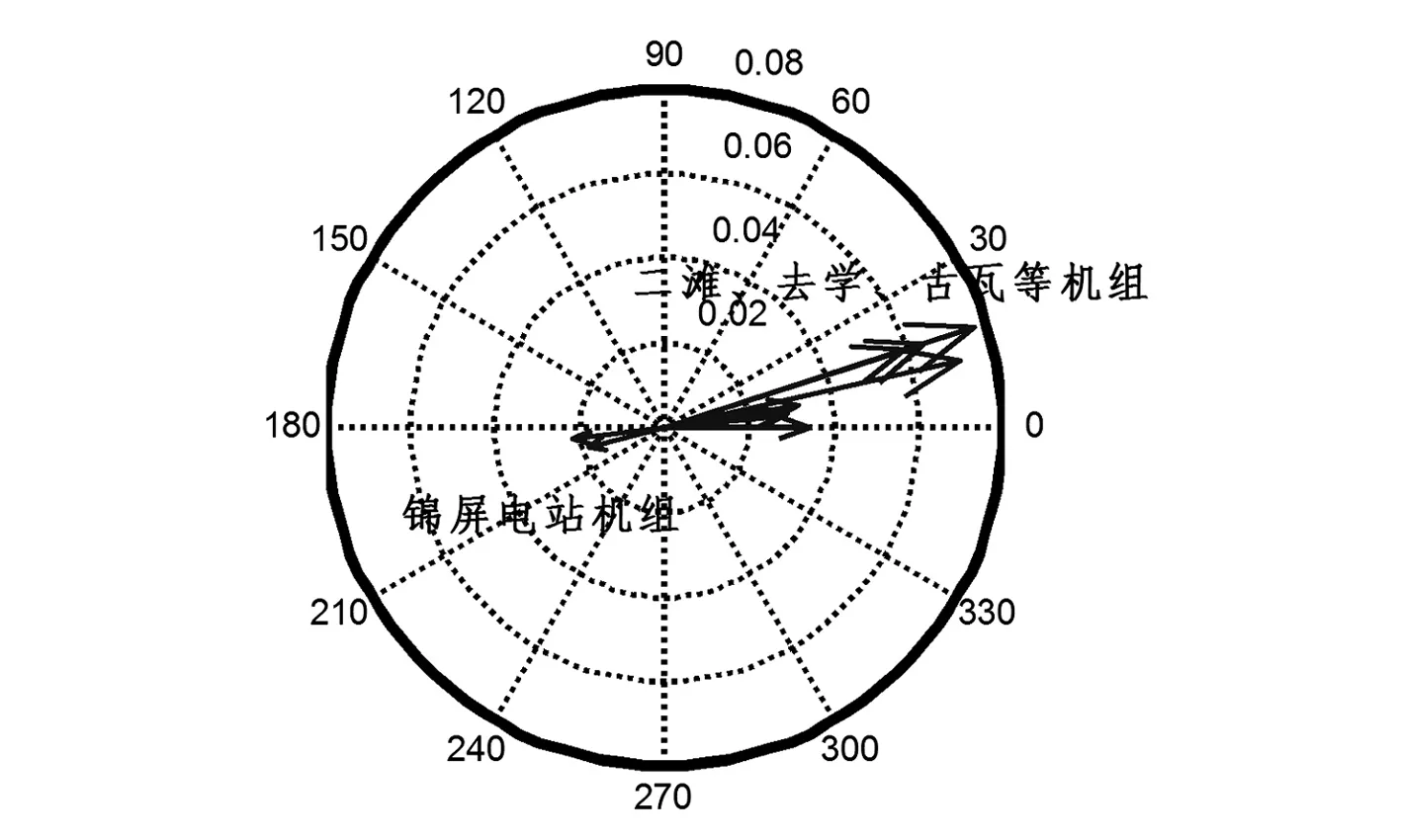
圖4 錦屏對鄉城的振蕩模態

5) 九石雅機組對康定機組模式

該振蕩模式的頻率為0.877 Hz，阻尼比為0.047，主要表現為九石雅、瀑布溝和丹巴、康定地區間的振蕩，機組模態分布圖如圖5所示。

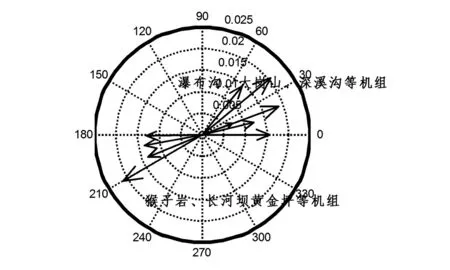
圖5 九石雅對康定的振蕩模態

6) 川渝主網對華中、河南模式

該振蕩模式的頻率為0.33 Hz，阻尼比為0.041，主要表現為川渝主網和華中電網間的振蕩，機組模態分布圖如圖6所示。

3.2 枯大方式下的振蕩模式分析

進一步對四川電網2017年枯大方式下的低頻振蕩特性進行分析，通過PSASP軟件計算，共得到3個機電振蕩模式，其對應的特征值如表2所示。

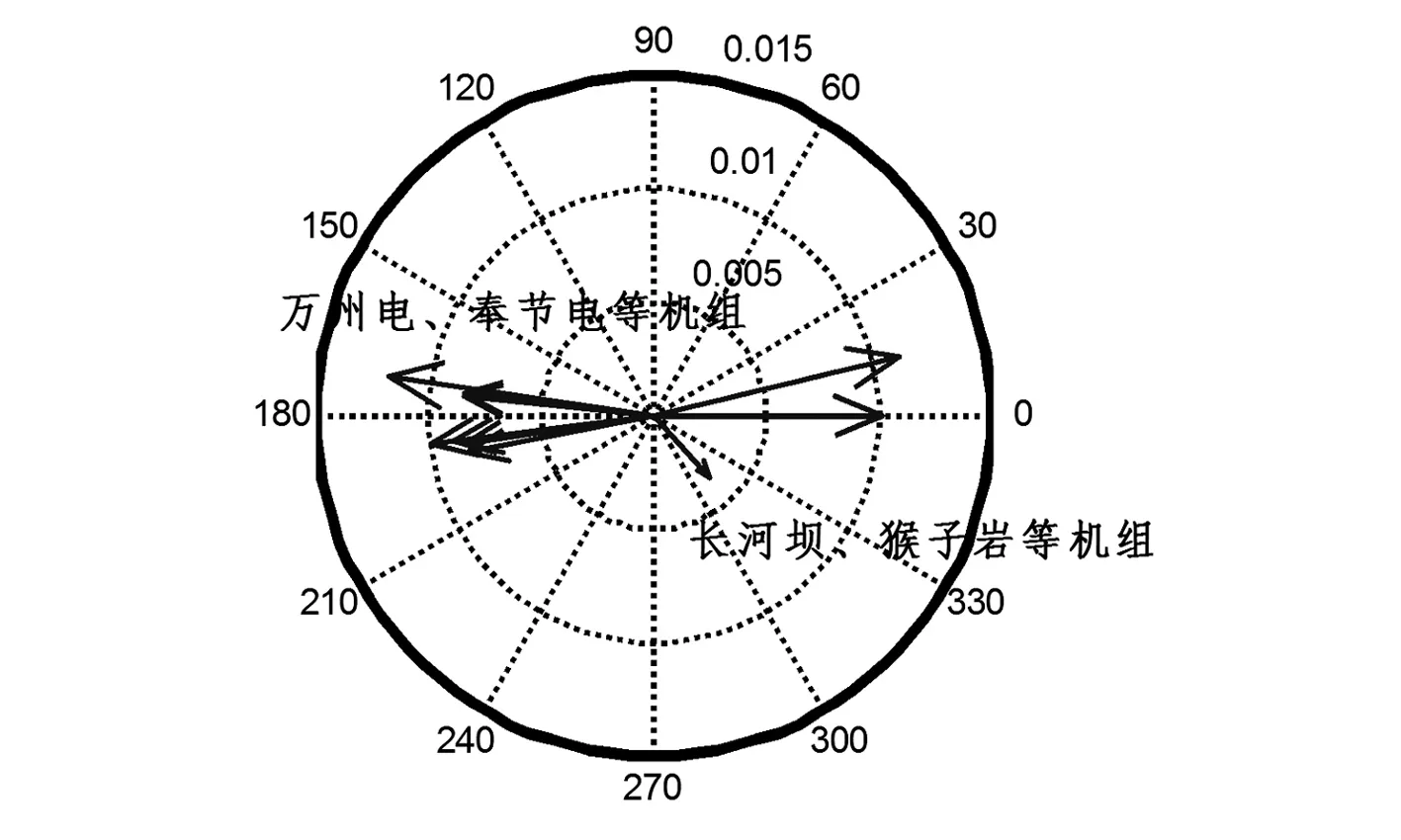
圖6 錦屏對鄉城的振蕩模態

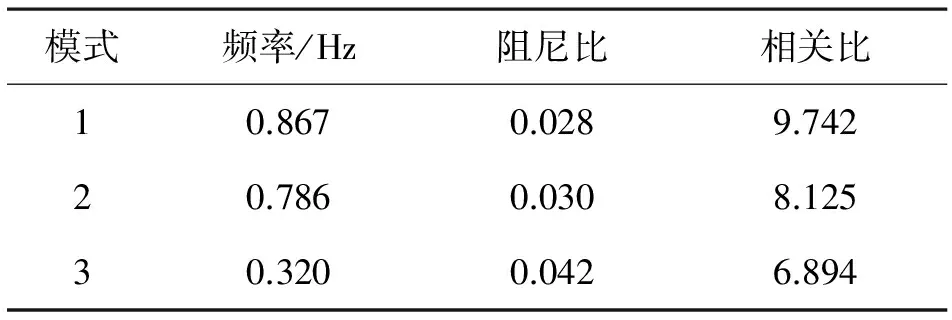
表2 枯大方式下存在的低頻振蕩模式信息

結合表2和模態分析結果可知，振蕩模式1表現為鄉城、木里對溪洛渡、向家壩間的振蕩，模式2表現為丹巴、康定對鄉城、二灘間的振蕩，模式3表現為川渝主網和華中電網之間的振蕩。從不同方式下的低頻振蕩結果可以得出以下結論： 兩種典型方式下，四川電網主要呈現出鄉城、木里對溪洛渡、向家壩，丹巴、康定對鄉城、二灘以及川渝主網對華中電網等典型的振蕩模式； 機組PSS投入情況下，上述振蕩模式的阻尼比均超過3%，說明實際運行中機組PSS的投入至關重要。

4 大擾動時域仿真及驗證

以四川電網對華中電網的振蕩模式為例進行時域仿真驗證。經分析，尖山桃鄉尖側故障易引起特高壓解列，四川、湖北間可能出現動態失穩現象。圖7所示為尖山桃鄉桃側N-1故障后二灘機組和三峽機組間的功角差曲線。

采用滑動窗法[11]對該功角差曲線進行Prony分析。設單個數據窗時長為5 s，相鄰數據窗時間間隔為2 s，滑動窗區間為5～25 s，每個滑動窗內數據均采用兩種方法分別辨識振蕩模式的頻率和阻尼比，可得到9組辨識結果，其統計值如表3所示。

對比時域仿真分析和基于模型的分析結果(表2模式3)可知，兩種方法分析結果基本一致。對其他振蕩模式進行對比分析，可得到類似結論，因篇幅所限不再贅述。

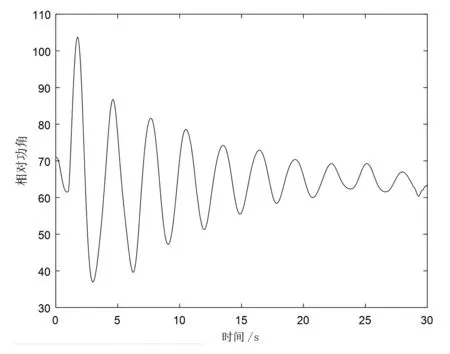
圖7 二灘機組和三峽機組間的功角差曲線

表3 基于仿真數據的辨識結果

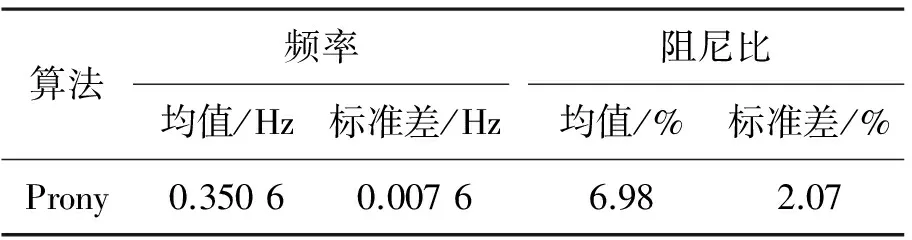
算法頻率均值/Hz標準差/Hz阻尼比均值/%標準差/%Prony0．35060．00766．982．07

5 結 論

1)PSS的投入對抑制低頻振蕩至關重要，若相關機組PSS退出，各模式阻尼比均大幅下降，甚至出現負阻尼模式，說明實際運行中機組PSS的投入至關重要。

2)進行了大擾動時域仿真，并與頻域分析進行了對比。結合實際工程經驗，應用傳統分析方法進行了參數的辨識。

3)因篇幅所限，未對低頻振蕩的抑制措施展開深入討論；考慮措施主要以投入PSS為主，但實際上，PSS只是改善了弱阻尼模式所對應的特征值，其對系統機電振蕩阻尼特性的改善主要體現在阻尼優化調節上，即優化了原系統的極點配置，并沒有增加系統的總阻尼，某些情況下，還是可能會出現低頻振蕩現象。對低頻振蕩的抑制，應從一次、二次系統統籌考慮，并充分運用現有新技術，研究有效的在線預警和控制方法[12]。

[1] 倪以信，陳壽孫，張寶霖．動態電力系統理論和分析[M]．北京:清華大學出版社,2002．

[2] F.P. Demello. Concepts of Synchronous Machine Stability as Affected by Excitation Control[J].IEEE Transaction on Power Apparatus and System,1969,88(4):316-329.

[3] 湯涌．電力系統強迫功率振蕩的基礎理論[J]．電網技術,2006,30(10):29-33．

[4] 韓志勇.電力系統低頻振蕩的分析和控制[D].北京:華北電力大學,2005.

[5] 韓志勇，賀仁睦，徐衍會，等．基于能量角度的共振機理電力系統低頻振蕩分析[J]．電網技術,2007,31(8): 13-16．

[6] 韓志勇，賀仁睦，馬進，等. 電力系統強迫功率振蕩擾動源的對比分析[J]. 電力系統自動化,2009,33(3):16-19.

[7] Lei Chen, Yong Min, and Wei Hu.An Energy-based Method for Location of Power System Oscillation Source[J].IEEE Transaction on Power System, 2013,28(3):828-836.

[8] 董清，梁晶，顏湘武，等．大規模電網中低頻振蕩擾動源的定位方法[J]．中國電機工程學報,2012,32(1):78-83.

[9] 檀斌，薛萬勝．多機系統混濁現象的研究[J]．電力系統自動化,2001,25(2):3-8.

[10] Wen-Show Kao, KAO The Effect of the Low-frequency Oscillations Damping in Taipower System Experience w/wo Power System Stabilizer[C]. Power Engineering Society Summer Meeting,2001.

[11] 丁藍，薛安成，李津，等. 基于窗口滑動改進Prony算法的電力系統低頻振蕩識別[J]. 電力系統自動化,2010,34(22):24-28.

[12] 王超，李繼紅，李穎毅，等. 淮滬特高壓投產后的華東電網低頻振蕩特征分析[J].電力系統自動化,2013,37(18):120-125.

Taking the project interconnecting North China Power Grid with Central China Power Grid and East China Grid as the research background, the low-frequency oscillation mode of Sichuan power grid containing UHV transmission lines is studied. With a review and summary of several mechanism of low-frequency oscillation, the main low-frequency oscillation modes in Sichuan power grid with UHV transmission lines are summarized based on the analysis of different typical operation modes, and the importance of power system stabilizer (PSS) to suppress the oscillation frequency is demonstrated. By verifying and analyzing the comparison of both time domain and frequency domain, the typical experiences of parameter identification in the time domain simulation analysis are proposed. Finally, the focus and direction for the future research of low-frequency oscillation are forecasted.

ultra-high voltage (UHV); low-frequency oscillation; forced oscillation; power system stabilizer

TM712

A

1003-6954(2017)02-0019-05

2016-11-29)

張 航(1994)，碩士研究生，研究方向為交直流電網穩定性分析與控制。