不同隨機模型在GPS單歷元定位中解算性能分析研究

陳西斌

(1.長春市測繪院,吉林 長春 130021;2.中國礦業大學 環境與測繪學院,江蘇 徐州221116)

?

不同隨機模型在GPS單歷元定位中解算性能分析研究

陳西斌1,2

(1.長春市測繪院,吉林 長春 130021;2.中國礦業大學 環境與測繪學院,江蘇 徐州221116)

基于GPS單歷元解算中隨機模型對解算精度的重要性,分析了常見的四種隨機模型建模條件。通過實測基線算例從流動站定位結果與定位標準偏差對它們進行分析與比較,明確了不同隨機模型的適用條件,為進一步提高GPS單歷元定位精度提供了理論基礎。

隨機模型;單歷元;內符合精度;track模塊;GAMIT

0 引 言

GPS單歷元定位中,由于觀測條件數少,組成方程個數較少,為得到精度較高的整周模糊度與協方差矩陣,選擇合適的隨機模型十分重要。在雙差方程解算中,選擇不同的隨機模型則賦予雙差觀測值的權不同,這不僅對基線解算有影響,而且關系到模糊度的搜索范圍。本文通過兩組具有代表性的短基線數據,將四種隨機模型進行定位精度分析與比較,得出一些有益的結論。

1 單歷元觀測方程隨機模型

不管是非差模型、雙差模型,還是組合模型,在組成改正數方程時,都需要觀測值的先驗信息,即觀測值的隨機模型。常見的雙差形式為測站間與衛星間作差,可表示為[1]

(1)

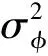
(2)

不同的隨機模型對解算函數模型影響很大,下文將分別介紹常見的隨機模型適用條件。

1.1 等權隨機模型

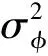
(3)

1.2 高度角隨機模型[3]

該隨機模型是將衛星處于某一時刻的高度角計算并建立的模型,其認為載波觀測值的精度與高度角相關。一般情況下高度角不同,信號傳播的路徑也不相同,隨著高度角增加,信號傳播路徑減少,大氣延遲誤差與多路徑誤差影響減弱。觀測值方差可以表示為高度角數值的函數:

(4)

f函數常見的有指數函數,正切函數,正弦函數,余弦函數。

1) 指數函數模型[3]

(5)

式中:σ0為衛星高度角為90°時載波觀測精度的均方差;a為比例系數;ε(t)為衛星高度角與時間成函數的數值;ε0為兩測站間共視衛星的高度角最大值。文獻[4]給出參考值，如表1所示。

表1 指數模型的參考值

2) 正弦函數模型

(6)

式中,E為衛星高度角。上述高度角隨機模型并不能很好地反映低高度角觀測精度,實際運用中常采用改進后的正弦函數模型[5]:

(7)

式中,a、b常取經驗值a=4 mm,b=3 mm.

3) 正切函數模型[6]

(8)

1.3 載噪比隨機模型

(9)

式中,Ci可用式(10)計算而得:

(10)

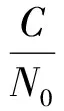
(11)

式中: Δ為理論值與實際觀測值差值;a為經驗系數一般取2.

1.4 信號強度隨機模型

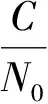
(12)

(13)

2 實驗分析

1) 實驗一

實驗數據來自中國礦業大學(徐州)南湖校區數據采集試驗場地,基線長約為91.3 m,基站與流動站高差較小,數據采樣間隔為1 s,采用天寶R8接收機,觀測時段為2014年10月2日,采用500個連續歷元,衛星截止高度角為10°,在后期數據轉換中增加CN0觀測值輸出。利用GAMIT軟件包中track模塊進行解算,對track模塊增加這四種隨機模型,得到流動站北(N)、東(E)、高程(U)三方向的定位結果,并利用內符合精度(STD)進行精度分析,如圖1所示和表2所示。

從圖1可以看出,等權模型在N、E、U三個方向定位結果最差,高度角模型、信號強度模型、載噪比模型定位結果相對較為平滑。

從表2可以看出,除等權模型以外的三種隨機模型中定位精度由高到低為載噪比模型、信號強度模型、高度角模型。這主要由于一般低高度角衛星的觀測值中噪聲較多,其中包括多路徑效應的影響,所以高度角隨機模型可以部分地減少多路徑的影響。與高度角模型相比,信號強度與載噪比更能夠反映載波觀測值的質量,尤其是衛星出現遮擋或者測站環境較復雜時,衛星的高度角也許數值較大,但其信號強度與載噪比數值比一般情況下較小。信號強度模型與載噪比模型解算結果大致相同,當數據轉換無載噪比數值輸出時,可以用載波強度代替載波噪聲比來求取觀測值的先驗信息。

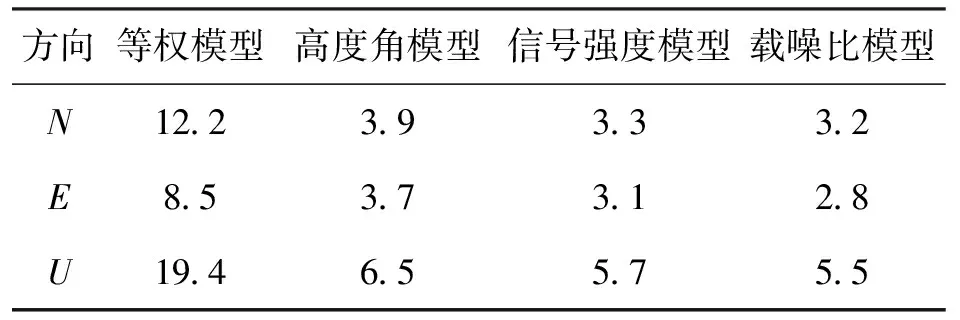
表2 四種不同模型計算的流動站 坐標STD值 單位：mm

2) 實驗二

實驗數據來自環測樓頂實驗場地,基準站架設在環測學院樓頂基準臺上,流動站架設在南湖校園內道路旁,基準站與流動站高差大約為24.87 m,基線長約為1.09 km,數據采樣率為1 s,衛星截止高度角設置為10°,解算軟件同實驗一,定位結果如圖2所示和表3所示。

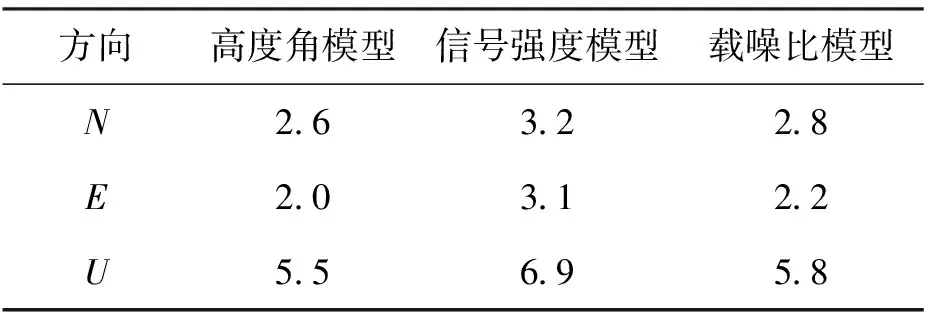
表3 三種不同模型計算的流動站 坐標STD值 單位：mm

從表3中可以看出,高度角隨機模型定位精度最高,信號強度與載噪比模型定位精度較差。這主要由于基準站與流動站存在著將近25 m的高差,從而雙差方程中殘余的對流層誤差數值較大。而由于高度角為對流層延遲的函數形式,因此觀測方程中使用高度角隨機模型有利于消除殘余大氣延遲誤差的影響。

3 結束語

通過利用等權模型、高度角模型、信號強度模型、載噪比模型對不同長度的、高度差較大的兩組基線進行數據處理,比較分析每種隨機模型的定位結果。可以得到以下結論:

1) 等權模型是一種理想化模型,盡量不采用該模型。高度角模型、信號強度模型、載噪比模型定位結果均優于等權模型。

2) 高度角隨機模型在基準站與流動站之間高差較大的情況下益適用,可更加有效地削弱殘余對流層延遲誤差;基線解算結果表明載噪比隨機模型與信號強度隨機模型的定位效果基本一致,當原始數據中有信號載噪比輸出時可替代信號強度建立載噪比隨機模型。

[1] 孟黎,徐杰.GPS觀測量的隨機模型研究[J]. 工程勘察, 2011(1): 73-77.

[2] 王振杰,方稚. GPS數據處理中實時隨機模型的估計方法[J]. 海洋測繪, 2014(6): 29-31，35.

[3] 徐鵬.基于衛星高度角的GPS觀測量隨機模型分析[J]. 測繪技術裝備, 2013(1): 40-42.

[4] 劉志強,黃張裕. GPS隨機模型最優不變二次無偏估計算法及實現[J]. 測繪科學, 2008，33(16): 158-159,80.

[5] 劉超,王堅,路鑫，等.GPS載波相位觀測值隨機模型的比較研究[J]. 測繪科學, 2010，35(6): 151-154.

[6] 郭秋英,蔡菲.GPS載波相位雙差觀測量隨機模型估計的新方法[J]. 山東建筑大學學報, 2009(5): 411-416.

[7] 李博峰,沈云中,徐培亮. 不同GPS接收機觀測值的隨機模型評估[J]. 科學通報, 2008，53(16): 1967-1972.

[8] 邱衛寧,齊公玉,鄒進貴，等. 不同隨機模型在GPS單歷元變形解算中的應用研究[J]. 測繪通報, 2011(10): 5-7.

[9] 張莎莎,鄭黃成,李信，等. 基于高度角的GPS單點定位隨機模型研究[J]. 城市勘測, 2014(5): 30-31,34.

[10] 戴吾蛟,丁曉利,朱建軍.基于觀測值質量指標的GPS觀測量隨機模型分析[J]. 武漢大學學報(信息科學版), 2008，33(7): 718-722.

Research on Different Stochastic Model in GPS Single Epoch Position Resolution

CHEN Xibin1,2

(1.ChangchunSurveyingandMappingInstitute,Changchun130021,China; 2.ChinaUniversityofMiningandTechnology,SchoolofEnvironmentalScienceandSpatialInformatics,Xuzhou221116,China)

Analyzing the common conditions of four kinds of stochastic model based on the importance of GPS single epoch solution. It is defined the applicability conditions of different stochastic models, according to analysising and comparing the results and std of mobile station from baseline example. it provides bases for further improving the positioning accuracy of GPS single epoch.

Stochastic model; single epoch; STD; track module; GAMIT

10.13442/j.gnss.1008-9268.2017.01.007

2016-11-11

江蘇高校優勢學科建設工程資助項目(編號：PAPDSA1102)

P228.4

A

1008-9268(2017)01-0034-05

陳西斌 (1987-),男,黑龍江虎林人,碩士,助理工程師,主要研究方向為GNSS數據處理與GAMIT、Bernese軟件研究等工作。

聯系人: 陳西斌E-mail:chenxibin1203@126.com