利用脈沖TDOA的雷達信號分選方法*

鄭惠文，黃建沖

(電子工程學院， 安徽 合肥 230037)

利用脈沖TDOA的雷達信號分選方法*

鄭惠文，黃建沖

(電子工程學院， 安徽 合肥 230037)

針對傳統雷達信號分選方法在復雜環境下分選雷達信號時對于信號形式的適應能力不強的缺點，提出一種對于雷達脈沖信號具有普適性的信號分選方法。該方法通過2個偵察站來偵察接收雷達信號，根據同一雷達輻射源的脈沖信號到達2個偵察接收站的時間差相同的原理進行信號分選。理論分析和計算機仿真表明該方法切實可行，能較好地解決復雜信號環境下雷達信號的分選難題。

雷達信號分選；到達時間；到達時間差；脈沖重復間隔；余弦定理；實時性

0 引言

20世紀20年代雷達就初具雛形，隨著人們對雷達的研究更加深入，對相關技術的要求也逐漸提高，慢慢出現了雷達信號分選技術。20世紀70年代，Campbell開始對復雜信號環境下的信號分選識別算法進行研究，參數范圍匹配法、試探法和統計平均估計法是當時最流行的方法。后續學者提出利用脈沖到達時間(TOA)進行基于脈沖重復間隔(pulse repetition internal, PRI)的去交錯實時分選算法[1-2]，在此基礎上延伸出累計差值直方圖算法[3]、序列差值直方圖算法[4]、復值自相關積分法[5]、平面變換法[6]等方法，也有學者在小波變換法[7]、支持向量機聚類算法[8]上取得了一定研究成果。在雷達數量少、樣式簡單時，這些方法尚能發揮作用，在雷達體制兼容、樣式繁多的情況下，這些方法的適應性較差。

為了解決雷達信號分選方法存在的問題，考慮通過對傳統信號分選方法進行改進或研究新的方法來提高算法的適應能力[9-10]。本文提出一種基于脈沖到達時間差(TDOA)的雷達信號分選方法，該方法對于脈沖信號形式具有普適性，且能準確地分離各個輻射源的脈沖信號，對獲取正確、完整的雷達對抗偵察情報意義重大。

1 基本原理

本文提出的基于脈沖TDOA的雷達信號分選方法利用2個偵察站來偵察接收雷達信號，通過分別測量雷達脈沖信號到2個偵察站的TOA，將2個TOA相減，得到脈沖信號到達2站的TDOA，按TDOA的不同對隨機交疊的脈沖序列進行分組，達到信號分選的目的。采用該方法分選雷達脈沖信號，不管信號形式多復雜，只要是由同一部雷達發射的信號，到達2個偵察站的TDOA必然相同，其原理示意如圖1所示。

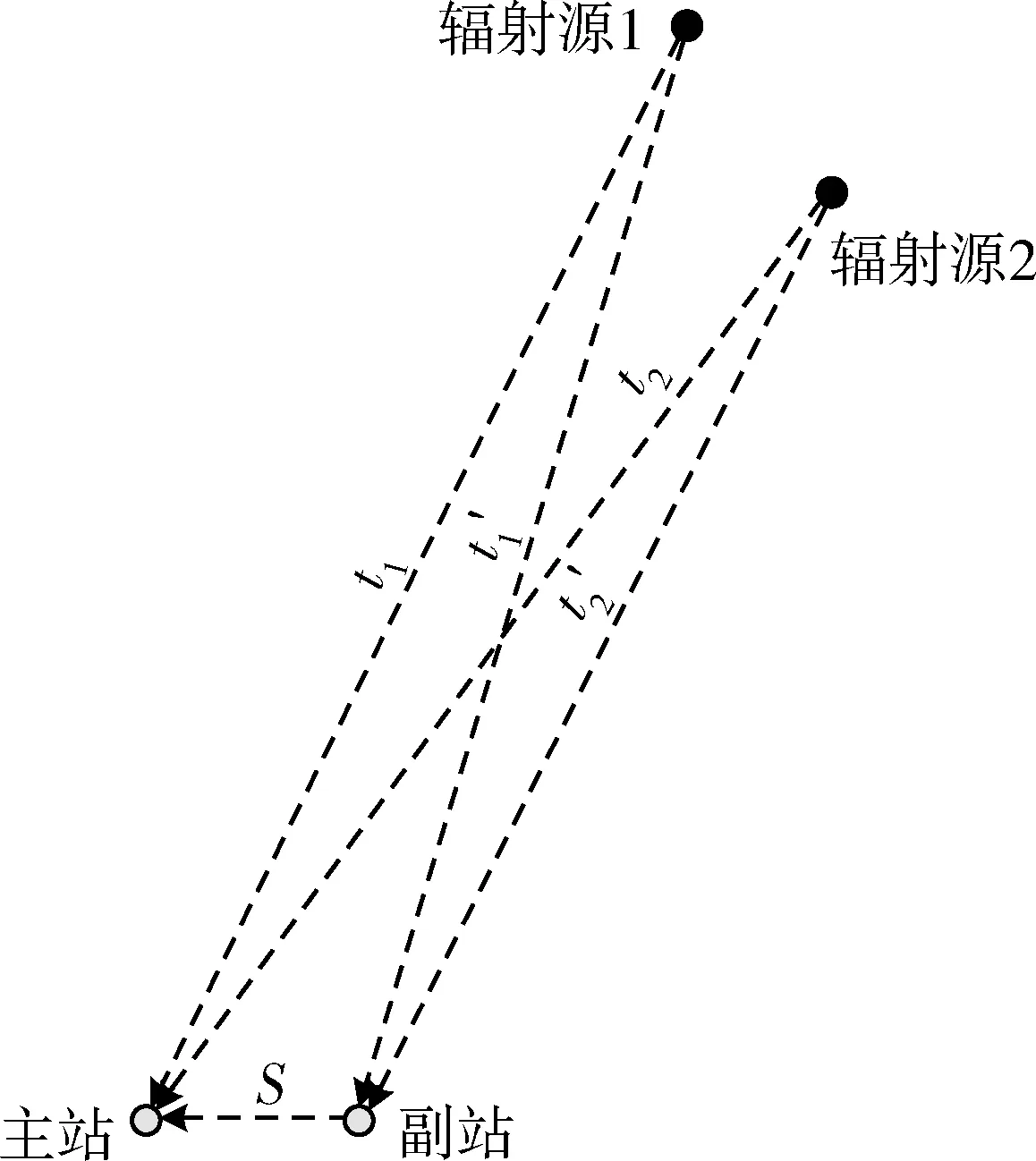
圖1 基于脈沖TDOA分選方法原理示意圖Fig.1 Schematic diagram of the principle of pulse TDOA sorting

2 方法流程

一段時間內，同一串脈沖信號被主站和副站接收到，副站將接收到的信號轉發至主站；在主站內對主站接收到的信號和副站轉發過來的信號進行高精度的TOA測量和快速測頻、脈寬、脈幅等參數，形成2組全脈沖參數，送入脈沖相關器提取時間差，得到TDOA。前圖1中只設了2個雷達輻射源，所以只存在2個TDOA值Δt1和Δt2，若接收到的脈沖信號來自M(M>2)個雷達輻射源，則會出現M個TDOA值Δt1，Δt2，…，Δtn(n=3,4,…,M)，根據TDOA的不同將全脈沖序列分成M組，每一組脈沖就是一部雷達發射的信號，完成信號分選。其流程如圖2所示。

圖2 基于脈沖TDOA雷達信號分選流程圖Fig.2 Flow chart of radar signal sorting based on pulse TDOA

3 案例分析及仿真

為驗證該方法的可行性，在這以6個輻射源為例對該方法進行分析并仿真。如圖3所示，假設主站和副站的地面距離為1 km，兩站由一條長為1 km光纖連接(由于地勢、交通等原因，所需的光纖長度可能會大于1 km，但光纖長度可事先測量，在這假設為直線連接)，以主站為原點、主站和副站連線的延長線為x軸作直角坐標系，用極坐標的形式表示6個輻射源的位置：A(100,119°)，B(115,101°)，C(105,87°)，D(120,80°)，E(125,68°)，F(110,59°)。

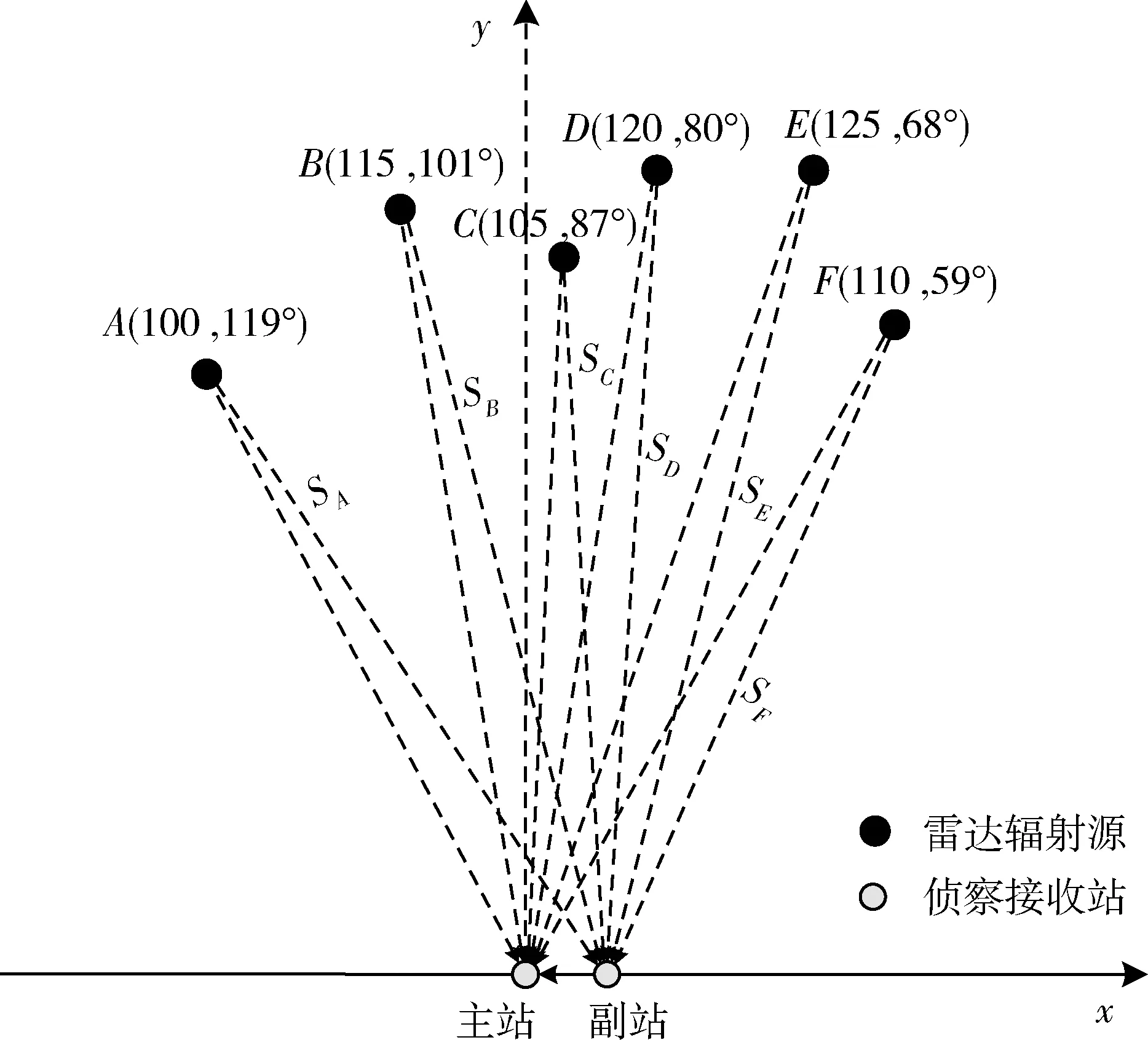
圖3 輻射源與偵察接收站的相對位置Fig.3 Relative position of radiation source and the reconnaissance receiving station

在由主站、副站和輻射源A構成的三角形中，已知輻射源A到主站、副站到主站的距離和二者的夾角，由余弦定理可求得輻射源A到副站的距離為

100.488 62 km.

(1)

副站接收輻射源A的脈沖信號并轉發到主站，實際傳輸距離為(100.488 62+1)km，但是副站把信號轉發到主站的時間可以事先測量，在計算TDOA時扣除即可，故不計算在傳輸時間內。所以，理論上輻射源A發射的脈沖信號到達主站和副站的TDOA為

ΔtA=(100-SA)/c=-1.628 73 μs.

(2)

式中：c為電磁波在真空中的傳播速度。

同理，可以計算出輻射源B,C,D,E和F的脈沖信號到達兩站的TDOA的理論值為

ΔtB=(115-SB)/c=-0.649 97 μs;

(3)

ΔtC=(105-SC)/c=0.158 62 μs;

(4)

ΔtD=(120-SD)/c=0.565 33 μs;

(5)

ΔtE=(125-SE)/c=1.237 19 μs;

(6)

ΔtF=(110-SF)/c=1.705 61 μs.

(7)

方法根據同一輻射源的脈沖到達兩站的TDOA相同分選信號，與雷達信號的復雜程度無關，所以在這以常規脈沖信號和脈沖參差信號為例進行分析。設輻射源A,B,C和D在一段時間內持續發射PRI分別為119,143,162和186 μs的常規脈沖信號，輻射源E,F發射子周期分別為104和191 μs,97和172 μs的二參差脈沖信號。在信噪比為20 dB時，常規PRI信號和二參差脈沖信號仿真圖如圖4所示。

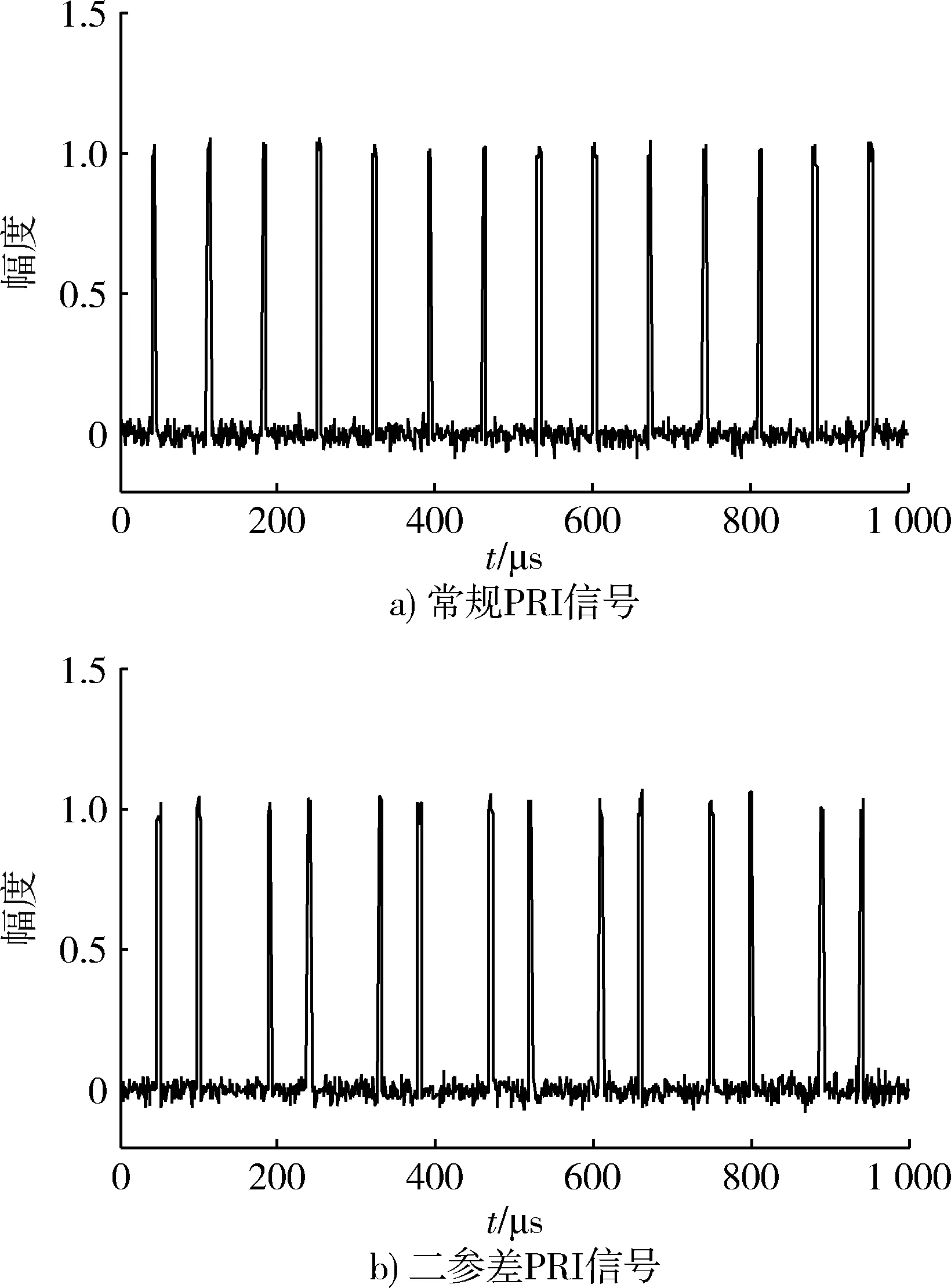
圖4 脈沖信號圖Fig.4 Pulse signal graph

利用該方法分選信號，必須使2個偵察接收機的距離很近(相對于接收機和輻射源之間的距離)，以保證在一段時間內兩接收機能接收到同一串雷達信號，在實際應用中很容易實現。雷達輻射源發射的脈沖信號在接收機中隨機交疊，通過計算機仿真模擬接收機接收到的雷達信號，在主站中截取同一段時間主站接收到的信號和副站轉發到主站的信號，其中副站轉發過來的信號是經過轉發校正的信號(即扣除了固定遲延)。在信噪比為20 dB時，主站和副站接收信號的仿真圖如圖5所示。

利用恒比觸發法[11]對接收機內的脈沖信號進行整形，可得到高精度整形脈沖序列。在主站內對經過整形的脈沖序列進行高精度的TOA測量和快速測頻、測脈寬、脈幅等參數，形成兩組全脈沖參數，送入脈沖相關器提取TDOA。本文在兩站之間提取TDOA的方式是基于統一信號的時差提取方式[12]，克服了多站系統中的時統誤差[13]，極大地提高了系統精度；副站信號轉發到主站的時間可以通過校正加以消除；測量脈沖TOA的方法[14]能做到高精度、實時測量，在目前硬件水平下，測量精度可以達到10-10s級；兩站之間提取TDOA和脈沖PRI提取的區別在于2個脈沖分別來自2個接收機，因此，必須考慮接收機的一致性誤差[15]，接收機的一致性誤差在目前的技術水平可以達到納秒量級。綜上所述，該方法的總誤差在納秒量級。

截取30 ms內主站和副站接收的雷達信號，測量各脈沖的TOA，并利用TOA求取脈沖到達兩站的TDOA，在計算結果上加上接收機一致性誤差ξ，即為實際情況中的TDOA值。在圖3所示的布站模型，TDOA的最大值為Δt0=1×103/c=3.333 33 μs(當且僅當輻射源與兩站三點一線的位置)。設Δt=Δt0+0.011=3.344 33 μs(冗余考慮測量誤差為1 ns，接收機一致性誤差為10 ns)為判決門限，利用Matlab進行仿真運算，求解脈沖到達兩站的TDOA，其中ξ由計算機程序生成為規定范圍內的誤差，輸出絕對值小于判決門限的TDOA值，仿真結果如圖6所示。

從仿真圖上可以看出，存在十幾個集中的TDOA值，但實際情況中應該只存在6個集中TDOA值，即存在虛假的TDOA值，稱虛假的TDOA點為諧波點。如果按照將TDOA的不同直接分選，則會分選出十幾部雷達，即出現增批現象，所以必須作一定處理。考慮從最密集的TDOA值開始，把符合該TDOA的兩站的脈沖全部從脈沖序列中扣除；再從剩下的脈沖序列中按最密集的TDOA值開始分選，直至分選完畢。

對仿真圖6中從最密集的TDOA開始分選，設定容差tTDOA±0.011→tTDOA，將分選出來的脈沖從序列中扣除，直至所有的脈沖分選完畢。分選過程如圖7所示。

從仿真結果可以看出，從最密集的TDOA值逐次分選，隨著被分選出的脈沖越來越多，諧波點就越來越少，直至分選完畢，諧波點消失。所以，利用該方法分選信號，只要能測得脈沖的TOA，獲得TDOA，就能完成信號分選。

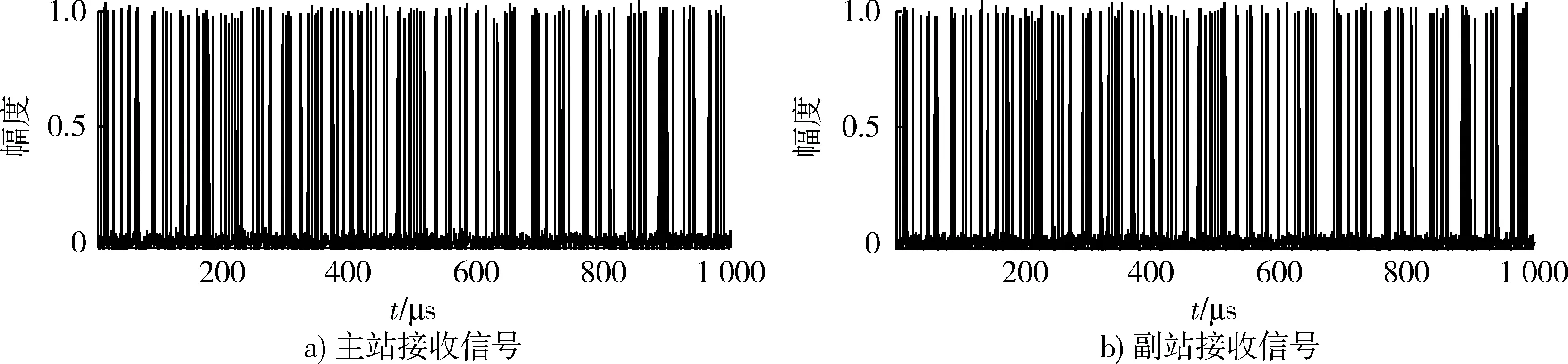
圖5 偵察接收站接收到的信號Fig.5 Signals received by reconnaissance receiving stations

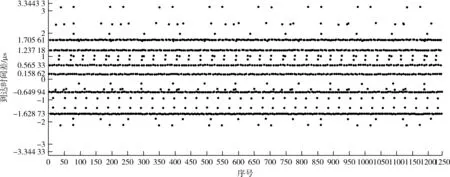
圖6 脈沖TDOA求解仿真結果Fig.6 Simulation results of pulse TDOA solution

圖7 逐次分選結果Fig.7 Simulation results of successive sorting

4 結束語

本文在分析當前雷達信號分選方法存在的問題的基礎上，提出了一種基于脈沖TDOA的雷達信號分選方法，然后介紹了該方法的基本原理和分選流程，最后通過計算機仿真實驗，驗證了算法的可行性。

方法分選信號與信號形式無關，即對于脈沖信號具有普適性。但仍然存在有待完善的問題：一方面，方法根據同一輻射源的脈沖信號到達兩站的TDOA相同分選信號，提高TOA測量精度可以進一步提高分選準確性；另一方面，對于TDOA的求解結果每次只能分選出一個輻射源，實時性還有待提高。

[1] DAVIES C L，HOLLAND P．Automatic Processing for ESM[J]. IEE Proc F Commun Radar&Signal Process，1982，129(3)：164-171.

[2] ROGERS J A V．ESM Processor for High Pulse Density Radar Environments[J]．IEE Proc F Commun Radar&Signal Process，1985，132(7)：621-624.

[3] MARDIA H K．New Techniques for the Deinterleaving of Repetitive Sequences[J]．IEE Proceedings Radar and Signal Processing，1989，136(4)：149-154．

[4] MILOJEVIC D J，POPOVIC B M．Improved Algorithm for the Deinterleaving of Radar Pulses[J]．IEE Proceedings and Signal Processing，1992，139(1)：98-104.

[5] NELSON D J．Special Purpose Correlation Function for Improved Signal Detection and Parameter Estimation[C]∥In Proceedings of International Conference on Acoustics，Speech，and Signal Processing，1993(4)：73-76．

[6] 趙仁建，龍德浩，熊平，等．密集信號分選的平面變換技術[J]．電子學報，1998，26(1)：77-82． ZHAO Ren-jian，LONG De-hao，XIONG Ping，et al．Plane Transform Technique for Dense Signal Sorting[J]．ACTA Electronic Journal，1998，26(1)：77-82．

[7] 韓俊，何明浩，翟衛俊，等．基于PRI變換和小波變換的雷達信號分選[J]．微計算機信息，2007，3(3)：164-166． HAN Jun，HE Ming-hao，ZHAI Wei-jun，et al．Sorting of Radar Signal Based on PRI Transfer and Wavelet Transfer[J]．Microcomputer Information，2007，3(3)：164-166．

[8] 童姍．復雜信號環境下雷達信號分選算法研究[D]．南京：江蘇科技大學，2014． TONG Shan．Research on Radar Signal Sorting Algorithm in Complex Signal Environment[D]．Nanjing：Jiangsu University of Science and Technology，2014．

[9] ZHAO Bao-chang，PENG Shi-rui，YU Chun-lai，et al．A New Method for Sorting Radar Signals Based on Coherency[C]∥ Third International Conference on Measuring Technology and Mechatronics Automation． Shanghai，China，2011: 170-173．

[10] Anant Ram，Ashish Sharma，Anand S Jalall．An Enhanced Density Based Spatial Clustering of Applications with Noise[C]∥International Advance Computing Conference．Patiala，India，2009：1475-1478．

[11] 潘繼飛，姜秋喜，畢大平．恒比觸發法在高精度雷達PRI測量中的應用[J]．現代雷達，2007，29(1)：64-67． PAN Ji-fei，JIANG Qiu-xi，BI Da-ping．Application of Invariable Comparison Triggering Method in High Precision Radar PRI Measurement[J]．Modern Radar，2007，29(1)：64-67．

[12] 王斌．時差定位系統高精度時差測量技術研究[D]．南京：南京信息工程大學，2009． WANG Bin．Study on the High-Definition Time Measurement for the Time-Difference Location System[D]．Nanjing：Nanjing University of Information Science & Technology,2009．

[13] 田中成，劉聰鋒．無源定位技術[M]．北京：國防工業出版社，2015． TIAN Zhong-cheng，LIU Cong-feng．Passive Locating Technology[M]．Beijing：National Defense Industry Press，2015．

[14] 孫杰，潘繼飛．高精度時間間隔測量方法綜述[J]．計算機測量與控制，2007，15(2)：145-147． SUN Jie，PAN Ji-fei．Methods of High Precision Time-Interval Measurement[J]．Computer Measurement & Control，2007，15(2)：145-147．

[15] 朱偉強，黃培康．高精度時差/頻差測量在雙站定位中的應用[J]．現代雷達，2009，31(3)：1-6． ZHU Wei-qiang，HUANG Pei-kang．Application of High Precision TDOA and FDOA Measurement Technique in Dual-Station Location System[J]．Modern Radar，2009，31(3)：1-6.

Radar Signal Sorting Method Utilising Pulse TDOA

ZHENG Hui-wen, HUANG Jian-chong

(Electronic Engineering Institute, Anhui Hefei 230037, China)

Aiming at the problem that the adaptability to signal form of traditional radar signal sorting methods are poor in complex signal environment， a new method of radar signal sorting is proposed，which is wildly applicable to radar pulse signal, by setting up two reconnaissance stations for receiving radar signal．Theoretical analysis and computer simulation indicate that this method is feasible and it can solve the problem of radar signal sorting in complex environment well．

radar signal sorting; time of arrival (TOA); time difference of arrival (TDOA); pulse repetition interval(PRI); cosine theorem; real time

2016-05-31；

2016-08-18 作者簡介：鄭惠文(1991-)，男，四川隆昌人。碩士生，主要研究方向為雷達對抗信號處理。

10.3969/j.issn.1009-086x.2017.02.034

TN957.5;TP301.6;TP391.9

A

1009-086X(2017)-02-0217-06

通信地址：230037 安徽省合肥市蜀山區黃山路460號503教研室 E-mail：307500035@qq.com