攔截高速機動目標分段最優制導律研究*

敦曉彪，李君龍

(1. 北京電子工程總體研究所，北京 100854； 2. 中國航天科工集團第二研究院，北京 100854)

攔截高速機動目標分段最優制導律研究*

敦曉彪1,2，李君龍1

(1. 北京電子工程總體研究所，北京 100854； 2. 中國航天科工集團第二研究院，北京 100854)

能量管理是在遠距離攔截高速、頻繁機動的目標時必須要考慮的問題，因為此時不僅攔截弧段長、攔截飛行時間也更久，攔截制導律設計不能不計能量代價地跟隨目標機動。通過將非線性彈目運動關系降階，在運用最優控制理論的基礎上，引入分段線性阻尼項，提出了一種針對高速、機動目標的最優制導律，可以滿足終端碰撞角約束及能量管理需求。該方法得到的制導律可令導彈在攔截高速機動目標時，對目標機動的敏感度隨彈目距離而變化，并分析了不同的分段線性阻尼對攔截彈道的影響。通過二維非線性仿真驗證了制導律的性能。

制導律；最優控制；碰撞約束；高速機動目標；高速；高加速

0 引言

高超聲速飛行器發展的主要支撐技術已實現突破性進展，從概念和原理探索階段發展到實驗應用階段，高超聲速巡航導彈、滑翔彈頭和高超聲速無人機等新型軍事武器在不斷發展成熟[1-2]，相對傳統彈道導彈目標，臨近空間目標的機動能力更強，跳躍滑翔的特性使其彈道的不確定性更高[3]。目標機動能力強，機動范圍大，是攔截制導律設計要面臨的新挑戰。目前攔截遠距離目標的制導律設計一般只考慮目標做常值機動，而目標跳躍滑翔機動時，要求攔截制導律設計不能只跟隨目標，而必須考慮自身的能量管理及攔截彈道優化問題[4]。目標被攔截時的碰撞角在導彈制導問題中是一個重要參數，它對戰斗部效能的影響極大。用傳統制導律，如比例導引，很難同時處理。

先前關于碰撞角控制主要包括最優制導律，改進比例導引類型的制導律。Kim提出了針對再入飛行器打擊地面固定目標和低速移動目標的最優控制律，滿足碰撞角誤差和脫靶量最小[5]。Ryoo的研究大都基于目標固定或者低速運動情形，包括對任意階動力學導彈，提出了固連在視線角坐標系下的系統最優控制律，并且給出了一種剩余飛行時間的計算方法[6-7]，以及采用剩余時間作為權重系數和控制指令組成指標函數來生成導彈彈道[8]。

Song針對攔截機動船只和速度變化的導彈，提出了碰撞角控制的最優制導律。假設目標機動相對較小且為常值。一個次優的估計濾波器被整合到解決方案中以得到的制導律需要的信息，包括垂直位置和相對于終端航向的相對速度，目標的航向角和角速率[9]。Kim提出了一個攔截機動目標的帶偏置比例導引律，且滿足碰撞姿態角約束。引入了一個時變項在比例導引制導律的視線轉率項中，并且不需要對剩余時間進行估計。仿真表明，制導律提供的自適應表現可以對抗慢速機動目標。花文華采用終端投影法將系統降階，基于零和微分對策原理推導出制導律。當目標作方波機動時，導彈需要的過載較大[10]。文獻[11-13]均給出了包括碰撞角約束的最優或次優制導律，但是攔截對象均都是固定或低速目標。

本文基于平面內交會幾何運動關系，構建攔截問題的線性化狀態方程。采用投影變換對系統降階，用最優控制理論進行求解，得到關于零控脫靶量和零控碰撞角線性形式的控制指令解析解。針對高速機動目標攔截問題，在控制指令中引入和彈目距離相關的分段線性阻尼項，對控制指令輸出進行管理，進而實現能量管理。討論了分段線性阻尼項參數對攔截彈道的影響，通過仿真驗證了制導律對攔截具有終端碰撞角約束的高速機動目標的性能。

1 攔截問題的數學描述

攔截彈選取側滑轉彎控制方式，并且保持滾動穩定，這樣導彈的運動模型可以分解為兩個相互正交的通道。如圖1所示為平面內末段交會幾何的示意圖，Oxz是笛卡爾慣性參考系，選取初始彈目連線(LOS0)為x軸，相對運動方程將在Oxz坐標系下線性化[14]。地面坐標系上的交會軌跡只需將上述坐標系旋轉一個初始的視線角即可。導彈和目標下標分別用M和T代表。速度、側向加速度、航跡角分別由v,a,γ表示。導彈目標之間的相對距離由r表示，x軸和彈目連線的夾角既為視線角，用θ表示。那么導彈目標的交會運動就可以看作是沿x軸逐漸接近的運動，那么z軸方向上的位移差就可以看作是脫耙量[15]。目標和x軸之間的相對位移表示為z。目標和導彈加速度在z軸方向上的分量分別表示為aMN,aTN，且滿足aTN=aTcosγT，aMN=aMcosγM。碰撞角為γI=γM+γT。

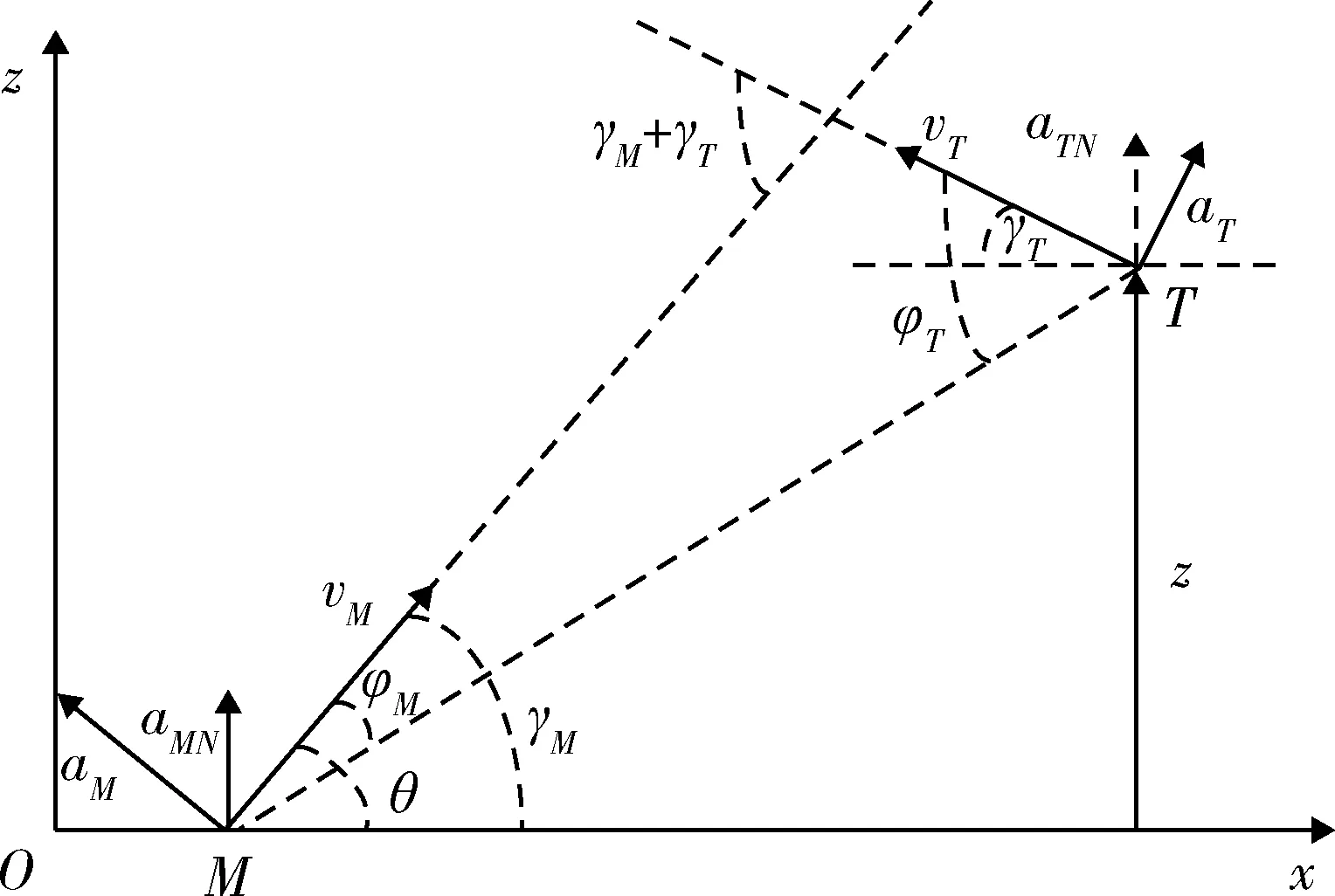
圖1 平面內交會幾何Fig.1 Planar engagement geometry

相對位移的導數和碰撞角的導數為

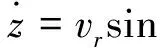
(1)

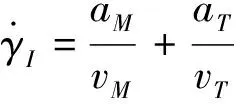
(2)

式中：

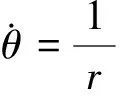
(3)

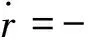
(4)

φM?γM-θ,

(5)

φT?γT+θ.

(6)

在每個仿真周期內，可以將目標和導彈視為勻速運動。另外，假設導彈、目標均具有一階側向機動動力學方程

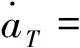
(7)

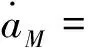
(8)

式中：τT，τM為目標和導彈的動力學時間常數；ωT，uM是目標和導彈的過載指令。

如果導彈和目標偏離碰撞三角形很小，也就是初始碰撞角和要求碰撞角大致相同，且目標的機動相對于目標速度較小，可以將問題線性化[16]。如果交會場景在初始時不滿足線性化的條件，可以在每一步仿真中進行線性化，也就是當時間間隔極小時，可以將問題看作是線性的。對于簡化后的線性交會問題，希望可以找到解析解，這樣就可以避免攔截彈在線求解黎卡迪方程。

線性化后，狀態向量為

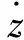
(9)

那么系統的狀態可以描述為

(10)

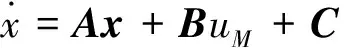
(11)

式中:

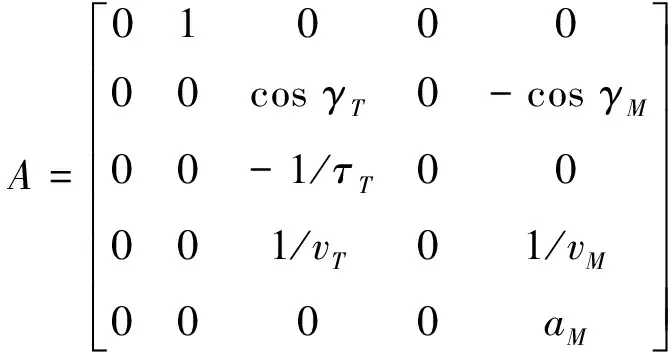
(12)

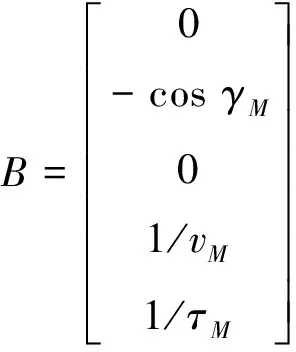
(13)

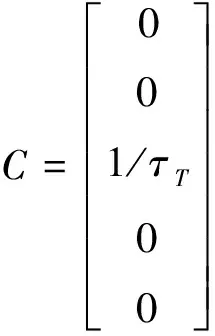
(14)

2 最優制導律

基于第1節構建的線性模型，進行最優制導律的推導。進一步將問題簡化，做如下假設：①已知目標未來的機動策略；②目標具有理想動力學模型，既ωT=aT。

選取最優制導律的二次型指標函數[17]

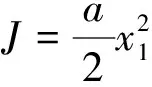
(15)

2.1 降階

為了將問題簡化，這里用投影轉換方法。定義一個新的狀態向量Z(t)滿足[20]：

(16)

其中，Φ(tf,t)為系統(11)的狀態轉移矩陣；D矩陣是一個常數矩陣

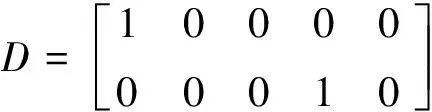
(17)

對式(16)進行求導，結合式(11)進行化簡，有

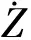
DΦ(tf,t)CaT=DΦ(tf,t)BuM.

(18)

考查新系統的終端狀態，既將t=tf代入式(16)中，得

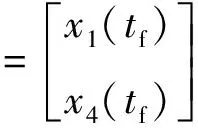
(19)

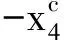
將新的狀態向量Z(t)代入性能指標式(15)中，有

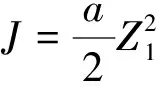
(20)

下面，運用最優控制理論對降階之后的問題求解。

2.2 最優制導律推導

根據最優控制理論，引入哈密爾頓函數

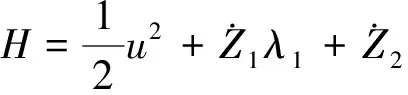
(21)

協態方程

(22)

滿足橫截條件

(23)

求解協態方程，得

(24)

令導彈具有理想動力學，即τM→0，則有

(25)

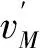
(26)

最優控制應滿足u*=arguminH，

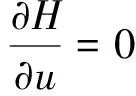
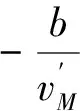
(27)

將式(27)代入式(26)，并從t到tf積分，結合式(19)中的邊界條件，有

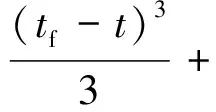
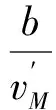
(28)

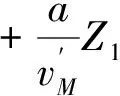
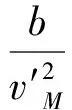
(29)

聯立式(28)，(29)，求解Z1(tf),Z2(tf)，再將結果代回到式(27)中，得到

(30)

制導增益

(31)

(32)

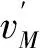
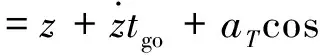
(33)

Z2(t)=tgoaT/vT+γT+γM,

(34)

剩余時間可以通過tgo=-r/vr計算。

2.3 分段優化

在本文討論的攔截場景是希望能夠遠距離攔截高速機動目標，目標在整個攔截制導過程中頻繁機動且機動幅度較大。2.2節推導出的最優制導指令是ZEM和ZEAE的線性函數，當目標機動時，ZEM和ZEAE改變劇烈，制導指令也出現較大變化，這在長弧段、長時間攔截過程中是不希望看到的。一方面，因為當制導指令大幅度改變時對于穩定控制是一個巨大的挑戰；另一方面，制導指令變化也不利于導彈的能量管理。因此，針對這類機動能力較強，且機動較為頻繁的目標，攔截制導律的設計不應只考慮滿足終端碰撞約束，而必須有更高一層的攔截策略。

根據攔截場景及彈目相對運動關系，提出如下策略：在攔截初段時，導彈可以幾乎不考慮目標機動而先選擇合適的姿態進行爬升；在攔截中段時，對目標機動進行一定程度的修偏，同時盡量保證導彈彈道平滑，以保留燃料為末段攔截提供充足機動能力；在攔截末段時，首要目的為滿足脫靶量要求，此時導彈應全力跟蹤目標機動，修正攔截偏差。

綜合2.2節中含碰撞角約束的最優攔截制導律及針對高速機動目標的攔截策略，考慮在最優制導指令中引入分段線性阻尼項，阻尼系數是彈目距離的分段線性函數，這樣制導指令就不只和ZEM，ZEAE相關，還受阻尼系數的影響。分段線性阻尼示意圖如圖2所示。式(35)為選取的分段線性形式阻尼。選取分段線性阻尼的好處在于，阻尼系數連續保證了制導指令連續，而多區間分段又保證了優化策略的多樣性。

(35)

式中:n為優化分段數；c為阻尼系數；cij(i=1,2,3,j=1,2)為待定系數；ri為彈目距離區間端點。

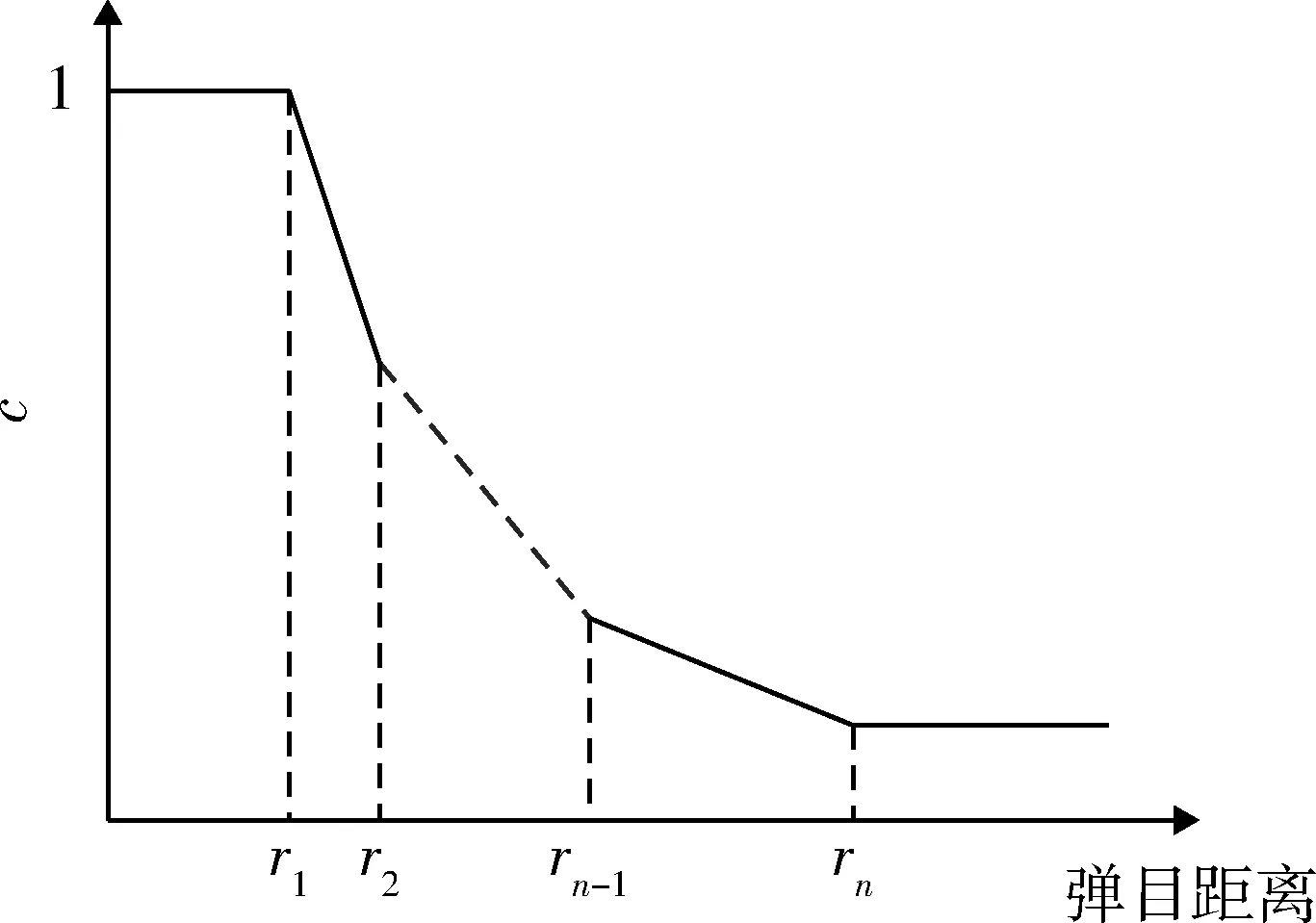
圖2 分段線性阻尼示意圖Fig.2 Schematic diagram of piecewise linear damping

ri的選取與初始彈目距離和彈目相對運動關系相關，它的物理含意就是將攔截彈道依據距離劃分區間，在不同區間內選取不同的優化策略，cij的選取取決于區間內攔截策略。

將阻尼系數c代入到制導指令式(30)中，有

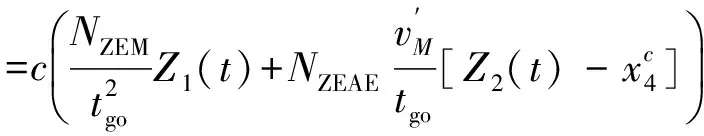
(36)

這樣就得到了引入分段線性阻尼項的最優攔截制導律。

3 仿真

3.1 常值機動目標

首先檢驗提出的制導律在有碰撞角約束的情況下攔截常值機動的目標的性能。選取不同的權重值b情況下，導彈的攔截彈道。彈目初始距離為2 km，目標速度為300 m/s，目標加速度為50 m/s2，導彈速度為500 m/s，期望的終端碰撞角γM+γT=10°。仿真結果如圖3所示。

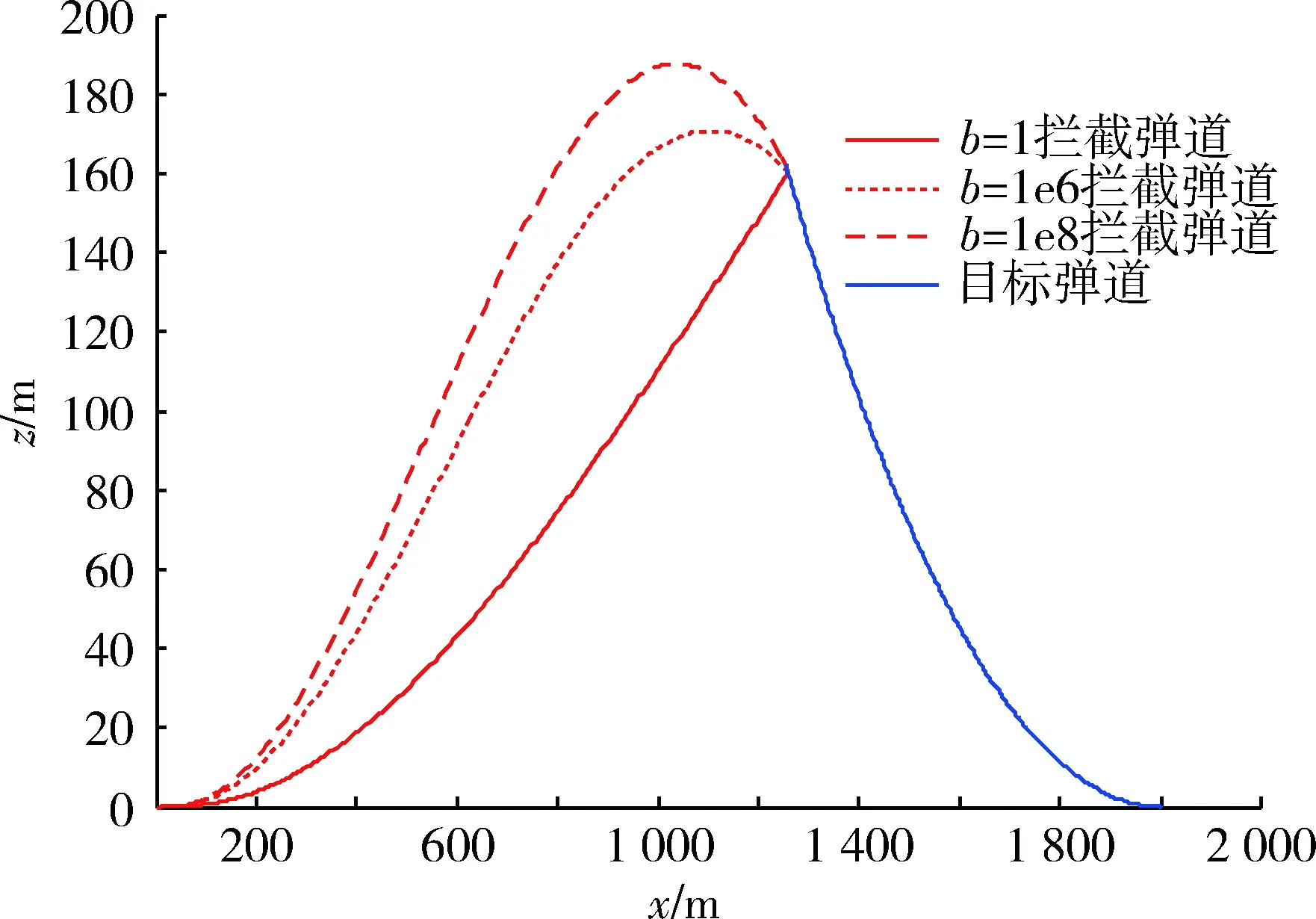
圖3 不同b值攔截彈道Fig.3 Intercept trajectories for various values of b

在攔截常值機動目標時，對過載不做約束的情況下，滿足了攔截要求，脫靶量小于2 m。其次，隨著b值的增加，碰撞角誤差在指標函數中的權重增大，碰撞角度誤差隨之降低。結果如表1所示。

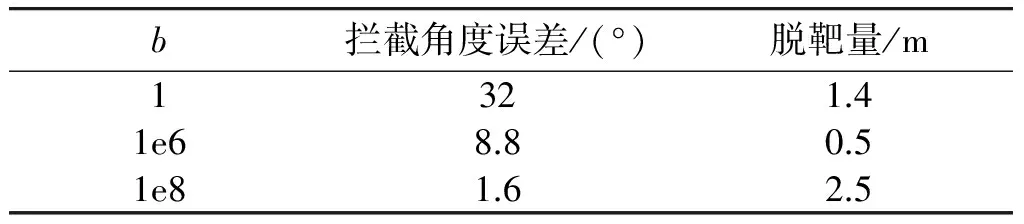
表1 b值不同脫靶量及角度誤差對比

3.2 高速高加速目標

驗證制導律對于高速機動目標的攔截性能，仿真初始條件假設目標初始位置為400 km遠，50 km高，導彈和目標的速度均為2 000 m/s，目標做正負50 m/s2的機動。機動模式為方波機動，如圖4所示。選取a=105,b=1，即脫靶量指標的權重遠遠大于終端碰撞角約束的權重。另外，給導彈施加了10g的過載限制。

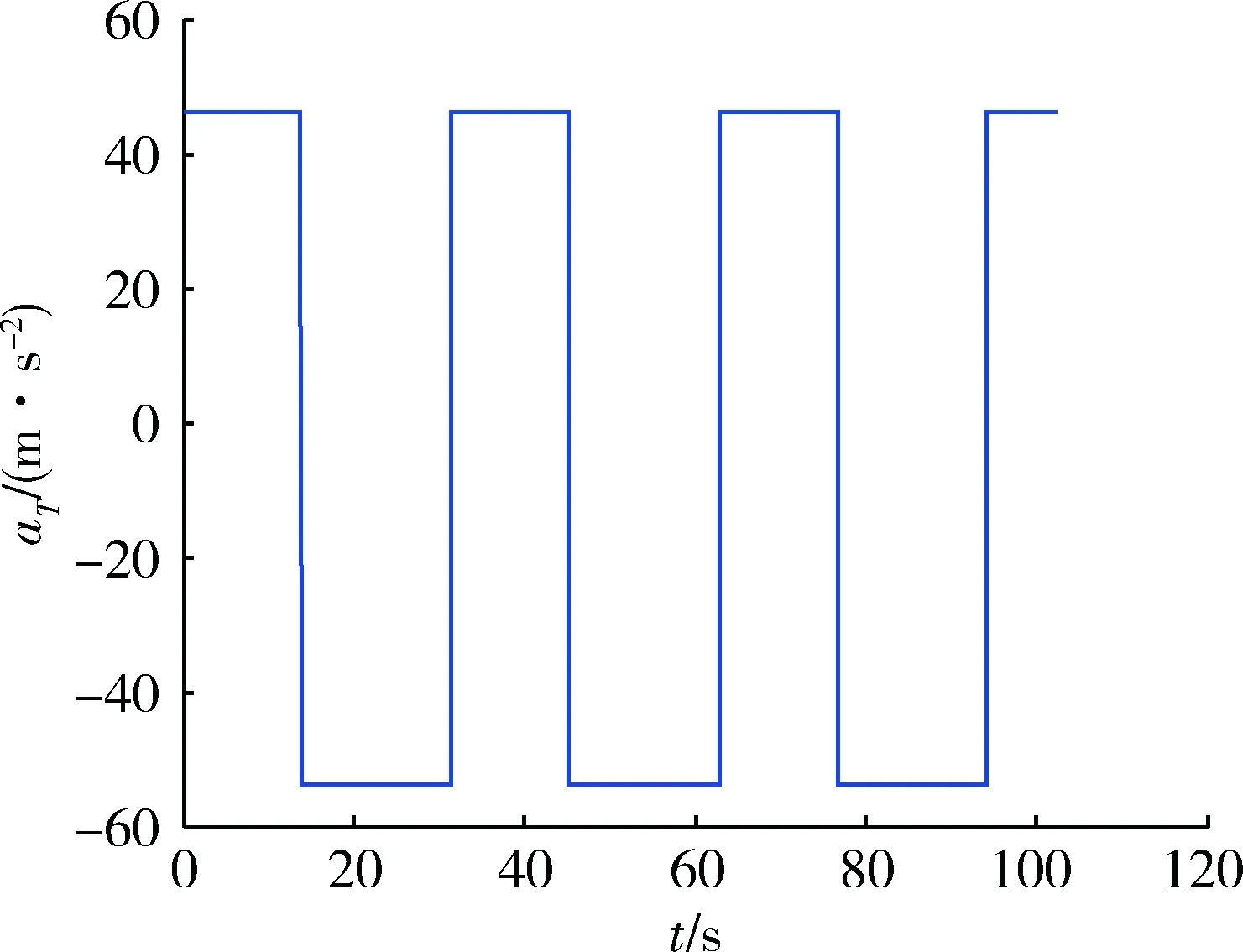
圖4 目標機動模式Fig.4 Maneuver model of target

3.2.1 區間端點不同

為了驗證分段線性阻尼最優制導律的性能，不失一般性地選擇式(37)中的阻尼項，分段區間數為3，分段區間為對稱形式。r1分別選取40，60，80，100 km。

(37)

式中：r0為初始彈目距離；r1為區間分段點。

阻尼值隨彈目距離變化如圖5所示。圖6為區間端點不同時的攔截彈道。

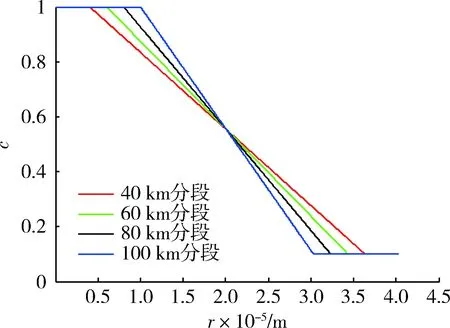
圖5 阻尼值隨彈目距離變化Fig.5 Damping values vs range between missile and target

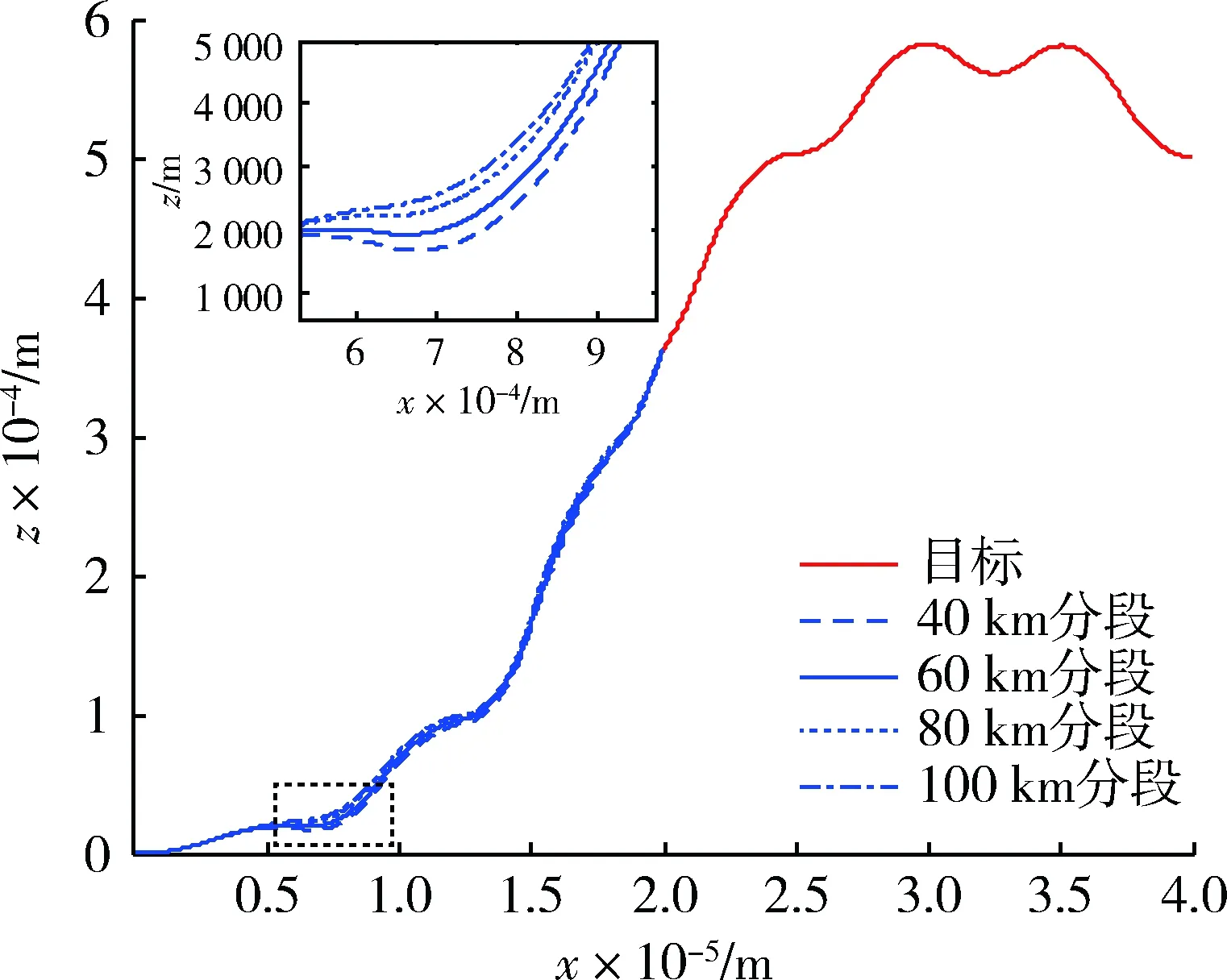
圖6 阻尼區間端點不同時的攔截彈道Fig.6 Intercept trajectories for different damping sub-interval endpoints

分析圖6可以看到，低阻尼系數持續的距離越長，彈道在前端彎曲越小，越平滑。

這是因為當阻尼系數較小時，導彈的控制指令對目標的機動不敏感，當目標做方波機動時，導彈較沒有完全去跟隨目標機動，而是兼顧自身能量管理的同時，對目標粗跟蹤，因此彈道較為平滑。

通過圖6中的局部放大圖可以看出，差別最大處也在1 km左右。表明區間端點不同對攔截彈道的影響不大。再對比4種情況的脫靶量，如表2所示，可以看到，當大阻尼保持較長時間時，會抑制后期導彈的機動能力，導致脫靶量較大。

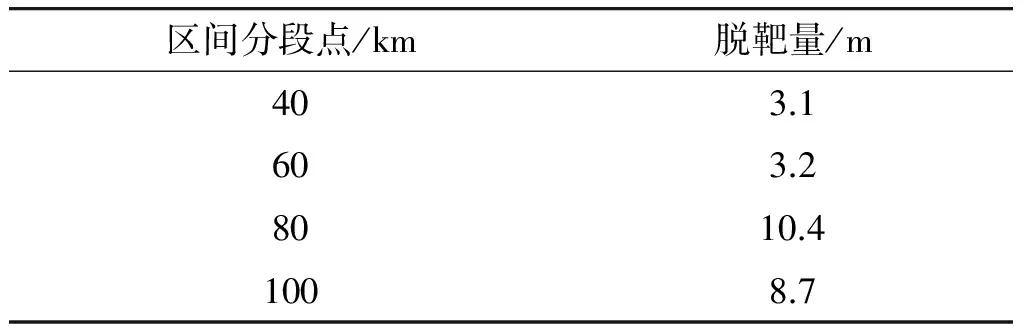
表2 區間端點不同脫靶量對比

3.2.2 初始段阻尼不同

選用式(38)中的阻尼項，當r>r0-60 km時，選取0.1，0.3，0.5 3種不同初始阻尼值和無阻尼項進行仿真。仿真中的阻尼系數隨彈目相對距離變化如圖7所示。攔截彈道對比結果如圖8所示。

(38)

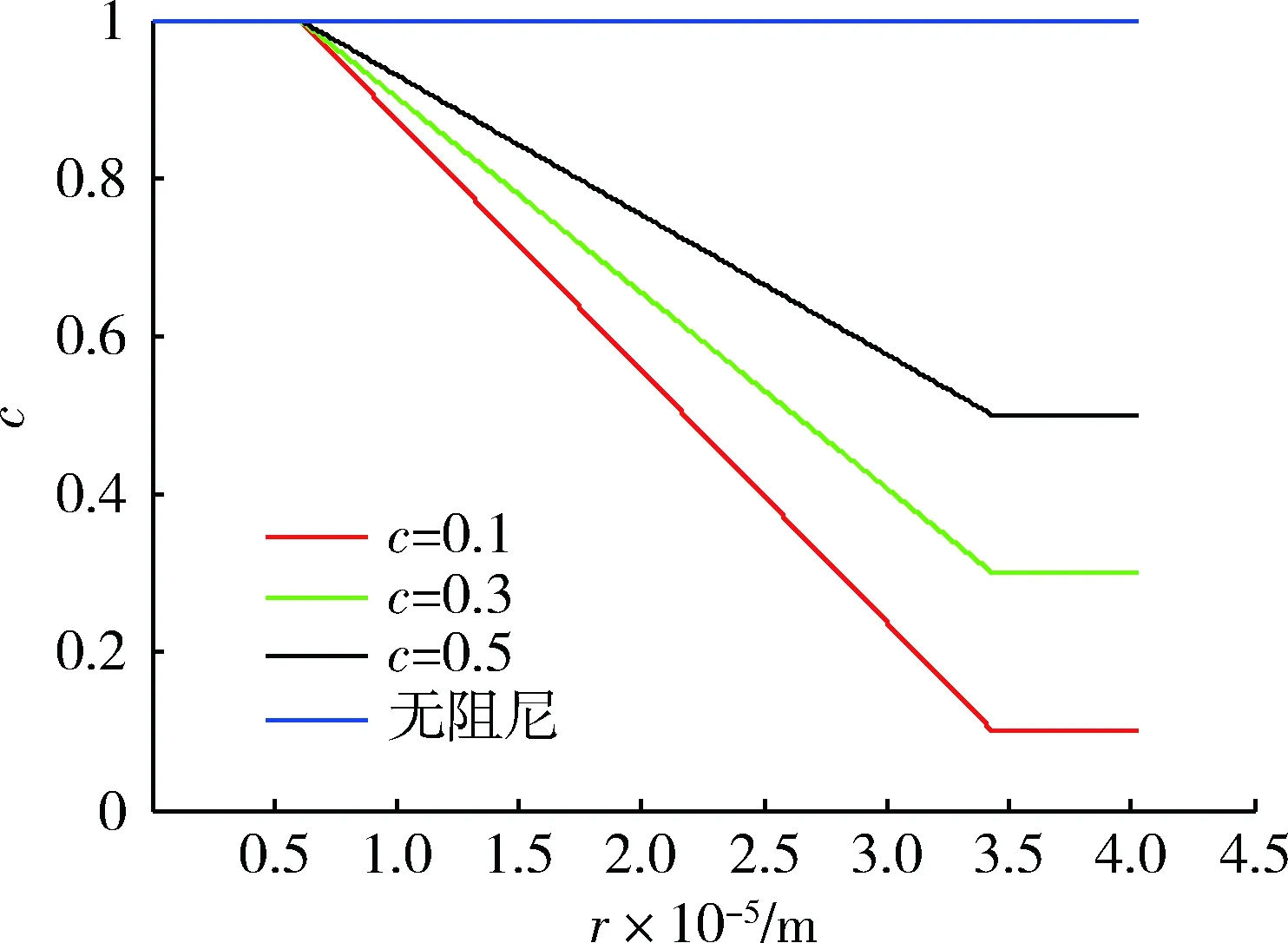
圖7 阻尼值隨彈目距離變化Fig.7 Damping values vs range between missile and target

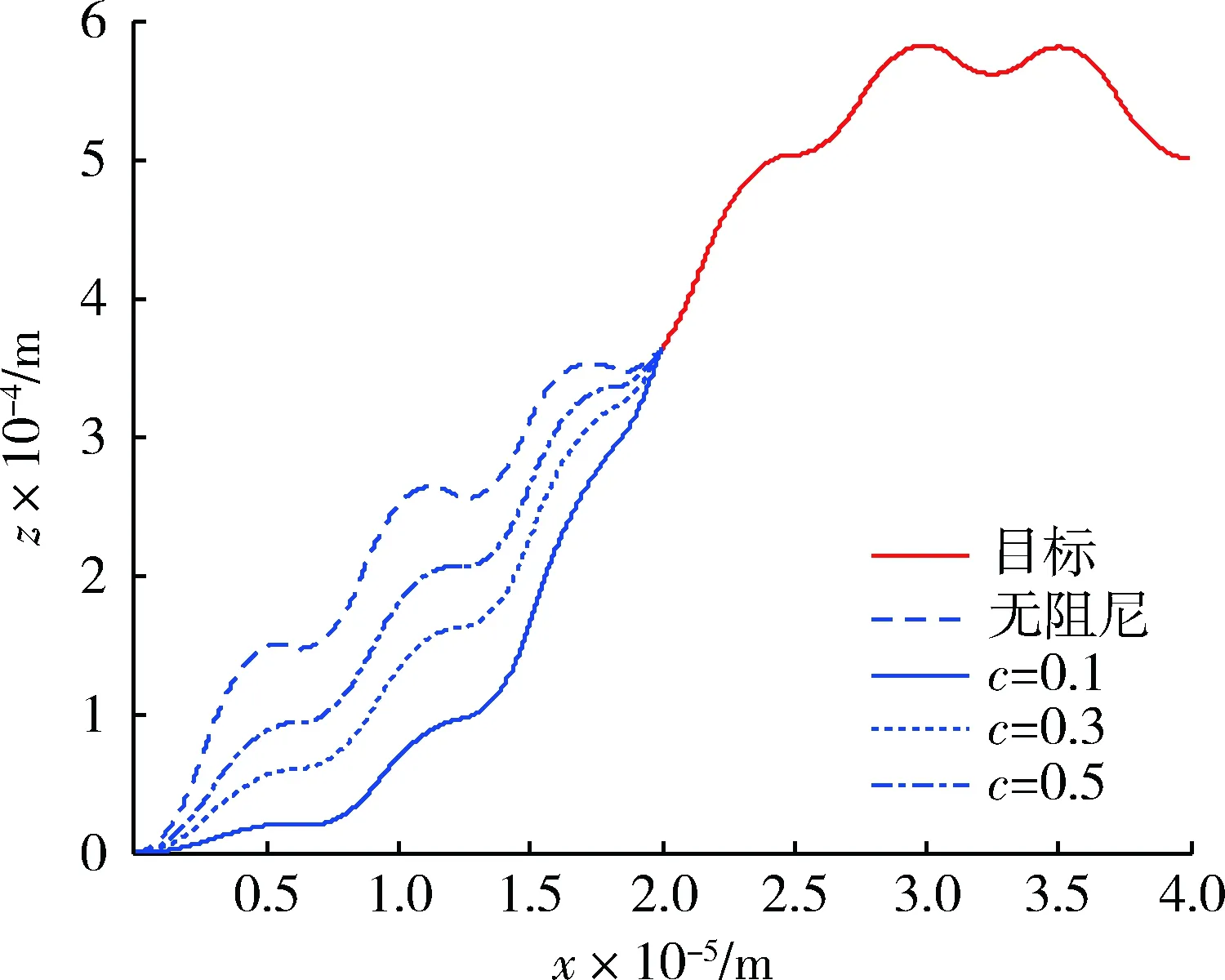
圖8 初始區間內阻尼值不同時的攔截彈道Fig.8 Intercept trajectories for various damping values in initial sub-interval

分析圖8中的彈道，可以看到在不加阻尼項的情況下，攔截彈道對目標機動十分敏感，導彈也幾乎隨著目標做方波機動。在增加阻尼項后，在攔截彈初期，導彈彈道明顯變得平緩，且隨著阻尼系數的變小，導彈的飛行高度也降低。這是因為在本次仿真中，目標初始的機動方向為z軸正向，當阻尼系數較小時，限制了導彈向z軸正向跟隨目標機動的控制指令。再分析圖中包含阻尼項的3條彈道，阻尼項較小時，彈道在初始段較低，而在攔截后段為了完成攔截目標，必須全力爬升；當阻尼系數較大時，導彈就會對目標機動敏感，失去了阻尼項期望達到的目的。通過表3可知，當初始段阻尼較小時，目標的大機動對導彈的影響反而減小，因此初始段的小阻尼值脫靶量更理想。

對比圖6及圖8，易見初始區間內阻尼值對彈道影響明顯大于區間端點對彈道影響。

表3 初始段阻尼不同脫靶量對比

3.2.3 控制指令對比

阻尼項區間端點不同時控制指令對比如圖9所示，初始區間阻尼值不同時控制指令對比如圖10所示。

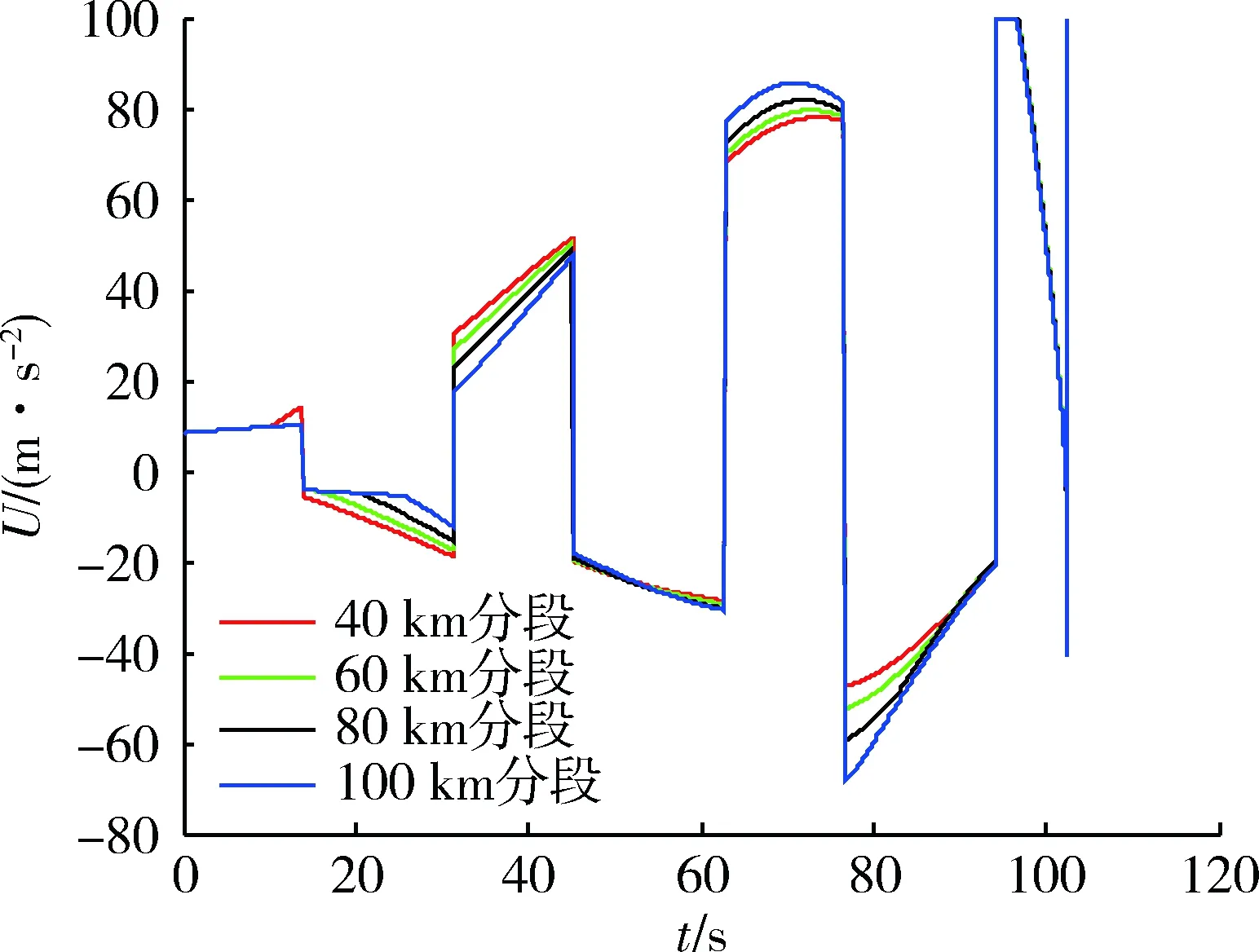
圖9 阻尼區間端點不同控制指令對比Fig.9 Control command comparison with different damping sub-interval endpoints

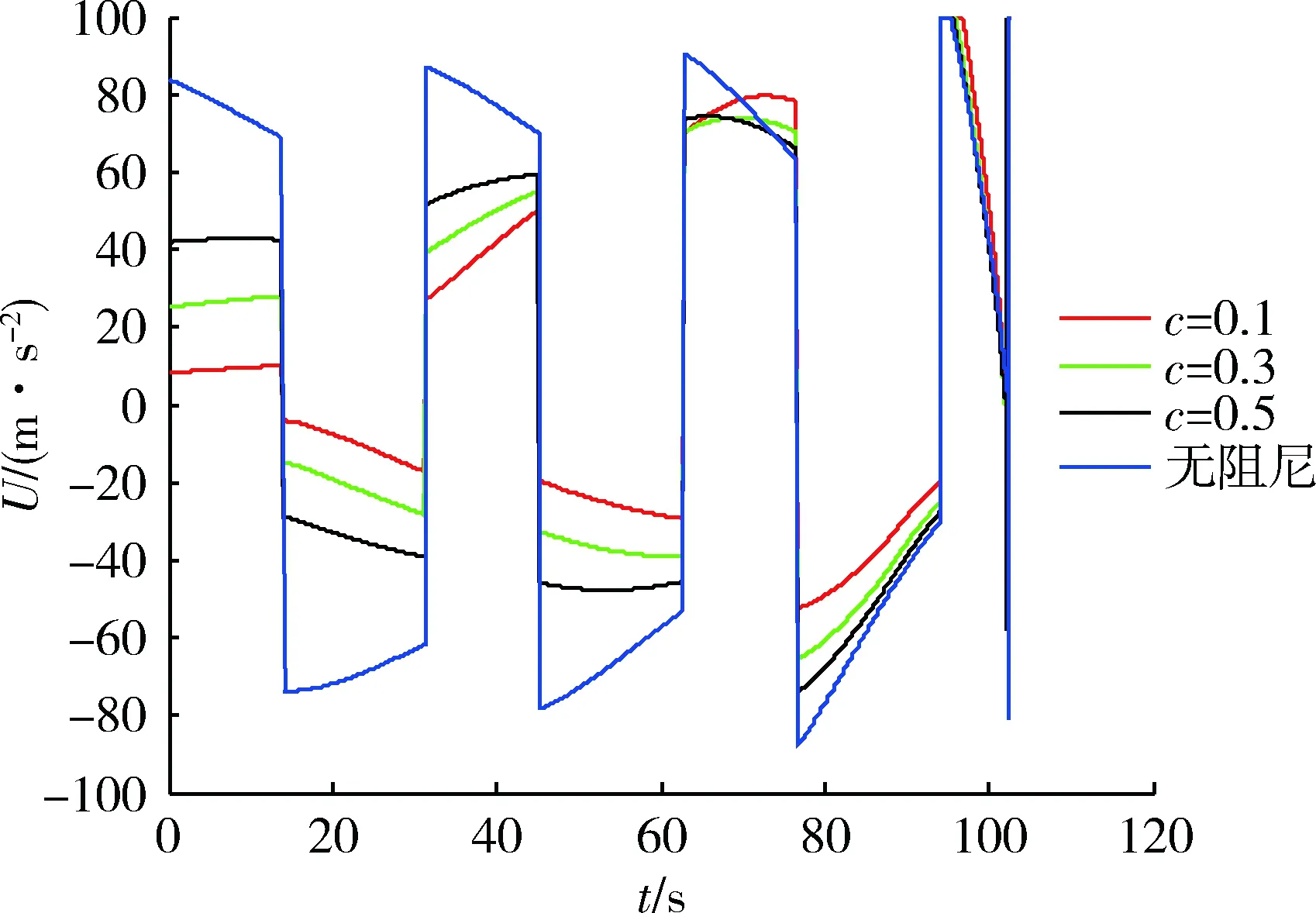
圖10 初始區間阻尼值不同時控制指令對比Fig.10 Control command comparison with different damping values in initial sub-interval

可以看到分段區間不同時，控制指令的差別很小，這和攔截彈道差別很小的結果是一致的；而初始段阻尼系數不同時，控制指令的差別較大，這和攔截彈道差別很大的結果是一致的。

4 結束語

主要研究了針對高速高加速目標具有終端碰撞角度約束的線性二次型最優制導問題。首先將交會問題分解到2個相互正交平面內分解，再將平面內的非線性攔截問題線性化；其次將攔截問題做降階處理，基于最優控制理論，進行制導律的推導。

針對目標作常值機動，驗證了制導律可以滿足碰撞角約束。針對目標作方波機動，為了達到導彈的燃料管理的目的，引入了和彈目距離相關的分段線性阻尼項，對分段區間不同和初始段阻尼系數不同的2類阻尼系統性能進行分析，結果表明分段區間不同對攔截彈道影響較小，而初始段阻尼系數對彈道影響較大。通過仿真驗證了提出的制導律可對高速高加速目標進行攔截，攔截彈道平滑，且實現了對燃料管理的目的，即當導彈距目標較遠時，不是全力跟蹤目標的機動，而是根據預測命中點大致跟蹤目標的軌跡，當導彈距目標較近時，再敏感目標的每一步機動，完成對目標的攔截。

本文的研究中導彈模型較為理想，后續研究將采用更為完善的導彈和目標模型。本文中考慮的過載約束較為簡單，只給導彈設定了一個常值過載約束，后續可以考慮更為復雜的過載約束。此外，本文的分段線性阻尼區間劃分的依據是彈目距離，后續可以考慮根據剩余攔截時間為分段依據。

[1] 黃華,劉毅,趙增亮,等. 臨近空間環境對高速飛行器影響分析與仿真研究[J]. 系統仿真學報,2013, 25(9):2230-2238 HUANG Hua, LIU Yi, ZHAO Zeng-liang, et al. Simulation of Influence of Near Space Atmosphere on Supersonic Vehicle[J]. Journal of System Simulation，2013, 25(9):2230-2238.

[2] 包云霞,張維剛,李君龍,等. 臨近空間武器對預警探測制導技術的挑戰[J]. 現代防御技術, 2012, 40(1):42-47. BAO Yun-xia, ZHANG Wei-gang, LI Jun-long, et al. Challenge and Consideration of Early Warning Detection & Guidance Technique of Near Space Weapons[J]. Modern Defence Technology，2012, 40(1):42-47.

[3] 戴靜,程建,郭銳. 臨近空間高超聲速武器防御及關鍵技術研究[J]. 裝備指揮技術學院學報, 2010, 21(3):58-61. DAI Jing, CHENG Jian, GUO Rui. Research on Near Space Hypersonic Weapon Defense System and the Key Technology[J]. Journal of the Academy of Equipment Command & Technology, 2010, 21(3):58-61.

[4] 呼衛軍,周軍. 臨近空間飛行器攔截策略與攔截武器能力分析[J]. 現代防御技術, 2012, 40(1):12-15. HU Wei-jun, ZHOU Jun. Analysis of the Interception Strategy of the Near Space Vehicle and Capability of the Interception Weapon[J]. Modern Defence Technology, 2012, 40(1):12-15.

[5] KIM M,GRIDER K V. Terminal Guidance for Impact Attitude Angle Constrained Flight Trajectories[J]. IEEE Trans. on Aerospace and Electronic Systems, 1973, 9(2): 852-859.

[6] RYOO C K, CHO H, TAHK M J. Closed-Form Solutions of Optimal Guidance with Terminal Impact Angle Constraint[C]∥Proc. of the 2003 IEEE International Conference on Control Applications, Istanbul, Turkey, June 25, 2003.

[7] RYOO C K, CHO H, TAHK M J. Optimal Guidance Laws with Terminal Impact Angle Constraint[J]. Journal of Guidance Control and Dynamics, 2005, 28(4): 724-732.

[8] RYOO C K, CHO H, TAHK M J. Time-to-Go Weighted Optimal Guidance with Impact Angle Constraints[J]. IEEE Trans. on Control System Technology, 2006, 14(3): 483-492.

[9] SONG T L, SHIN S J, CHO H. Impact Angle Control for Planer Engagements[J]. IEEE Trans. on Aerospace and Electronic Systems, 1999, 35(4): 1439-1444.

[10] 花文華,劉楊,陳興林,等. 具有終端約束的線性二次型微分對策制導律[J]. 兵工學報, 2011, 32(12)： 1448-1455. HUA Wen-hua, LIU Yang, CHEN Xing-lin, et al. Linear Quadratic Differential Game Guidance Law with Terminal Constraints[J]. Acta Armamentarii，2011, 32(12): 1448-1455.

[11] DAS P G,PADHI R. Nonlinear Model Predictive Spread Acceleration Guidance with Impact Angle Constraint for Stationary Targets[J]. International Federation for Automatic Control Proceedings, 2008, 17(1): 13016-13021.

[12] RATNOO A, GHOSE D. Impact Angle Constrained Interception of Stationary Targets[J]. Journal of Guidance Control and Dynamics, 2008, 31(6): 1816-1821.

[13] OZA H, PADHI R. A Nonlinear Suboptimal Guidance Law with 3D Impact Angle Constraints For Ground Targets[C]∥Proc. of AIAA Guidance Navigation and Control Conference 2010: 8185-8191.

[14] TAUB I, SHIMA T. Intercept Angle Missile Guidance under Time Varying Acceleration Bounds[J]. Journal of Guidance Control and Dynamics，2013, 36(3): 686-699.

[15] SHIMA T, SHINAR J. Time-Varying Linear Pursuit-Evasion Game[J]. Journal of Guidance, Control and Dynamics, 2002, 25(3): 425:432.

[16] RUSNAK I, WEISS H, ELIAV R, et al. Missile Guidance with Constrained Terminal Body Angle[J]. IEEE Trans on Aerospace and Electronic Systems, 2014, 50(2): 45-49.

[17] SHAFERMAN V, SHIMA T. Linear Quadratic Guidance Laws for Imposing a Terminal Intercept Angle[J]. Journal of Guidance Control and Dynamics，2008, 31(5): 1400-1412.

[18] SHIMA T. Intercept-Angle Guidance[J]. Journal of Guidance Control and Dynamics, 2011, 34(2): 484-492.

[19] TAUB I. Intercept Angle Guidance Under Time Varying Speed[C]∥AIAA Guidance Navigation and Control Conference, 2015-0090.

[20] WEISSM M, SHIMA T. Optimal Linear-Quadratic Missile Guidance Laws with Penalty on Command Variability[J]. Journal of Guidance, Control and Dynamics, 2015, 38(2): 226-237.

Piecewise Optimal Guidance Law for Intercepting High-Speed Maneuvering Targets

DUN Xiao-biao1,2, LI Jun-long1

(1. Beijing Institute of Electronic System Engineering, Beijing 100854, China; 2. The Second Research Academy of CASIC, Beijing 100854, China)

Energy management issue is a necessary consideration when remotely intercepting a high-speed and frequently maneuvering target, because the interception arc is long, and interception time is also long, therefore the guidance law design can not make all costs to follow the target. By reducing the nonlinear kinematics order, as well as on the basis of using optimal control theory and introducing a piecewise linear damping term, an optimal guidance law to intercept high-speed maneuvering target to meet the end impact angle constraint and energy management demand is proposed. The proposed guidance law can change the sensitivity of target maneuvering with the missile-target distance. Meanwhile, the impact of intercept trajectory on different parameters damping is analyzed. The performance of the proposed guidance laws is proven by a nonlinear two-dimensional simulation.

guidance law; optimal control; collision constraint; high speed maneuvering target; high speed; high acceleration

2016-07-09；

2016-09-08 基金項目：有 作者簡介：敦曉彪(1989-)，男，河北石家莊人。博士生，主要從事導航、制導與控制方面研究。

10.3969/j.issn.1009-086x.2017.02.014

TJ765.1；TP391.9

A

1009-086X(2017)-02-0093-08

通信地址：100854 北京市142信箱30分箱 E-mail：dunxb@126.com