基于BP神經網絡的超磁致作動器建模與控制

王丹梅，馮偉峰

（西南交通大學電氣工程學院，成都 611756）

基于BP神經網絡的超磁致作動器建模與控制

王丹梅，馮偉峰

（西南交通大學電氣工程學院，成都 611756）

超磁致作動器的遲滯非線性是其應用的一大障礙，對此基于BP神經網絡建立超磁致作動器GMA的Hammerstein模型，在此模型基礎上，設計前饋逆補償與PID反饋控制相結合的復合控制策略。針對建模范圍內的所有單頻和復合頻率的輸入信號，控制器都能保證跟蹤控制效果。通過實驗實時跟蹤的結果進一步驗證建模和控制的效果。

遲滯非線性；超磁致作動器；BP神經網絡；Hammerstein模型

0 引言

基于磁致稀土，利用其能反應磁場變化作出形變的特性制作而成的執行器，稱為超磁致作動器（GMA, Giant Magnetostrictive Actuators），以棒狀結構的伸張縮反應磁場變化。由于超磁致作動器儲能效率高，遠高于鎳制品和壓電陶瓷，此外響應速度快，能夠及時以伸縮反應磁場。因此超磁致作動器常常應用在在微米級別的微位移精確控制領域中。但作動器表現出明顯的率相關性，難以得到精確模型、帶來控制效果變差等問題。

目前建模方法大致可以分為三種。根據超磁致物理作用機理的物理建模、根據系統輸入輸出的唯象建模、根據模擬人認知行為的智能方法建模。

對遲滯系統的控制方法，主要有逆補償控制、不直接求逆以及智能算法等方法，其中逆補償控制是最主要的方法。在反饋控制策略的研究中，如何使系統使用對象使用不確定性、滿足規定性能指標是學者常見研究方向。

1 超磁致作動器的建模與驗證

1.1 Hammerstein模型

由于率相關性系統直接建模不容易找到模型描述，本文使用Hammerstein建模思想，把系統拆分兩種有成熟控制方法的已知模型，這種方法可以描述大多數非線性系統。其中u、v分別為輸入、輸出，x是動態線性模塊輸入。

圖1 Hammerstein模型

Hammerstein模型的辨識可把前后兩個部分分別進行辨識。本文靜態部分采用BP神經網絡方法進行辨識，動態部分采用ARX（AutoRegressive eXogenous）模型。

1.2 BP神經網絡

神經網絡利用函數去逼近模型，屬于建模方法的智能方法建模類，通過大量數據的訓練過程，可以達到高精度的指標，使神經網絡建模方法能夠較好地描述超磁致作動器，方便控制。本文采用BP神經網絡建立超磁致作動器靜態非線性模型。

神經網絡只能逼近一對一映射或者多對一映射關系，而作動器的輸入與輸出之間具有多值映射關系，不能直接用神經網絡進行建模，因此本文采用基于擴展輸入空間的BP神經網絡模型，引入基本遲滯算子對輸入空間進行擴展，使神經網絡滿足一一對應的關系。

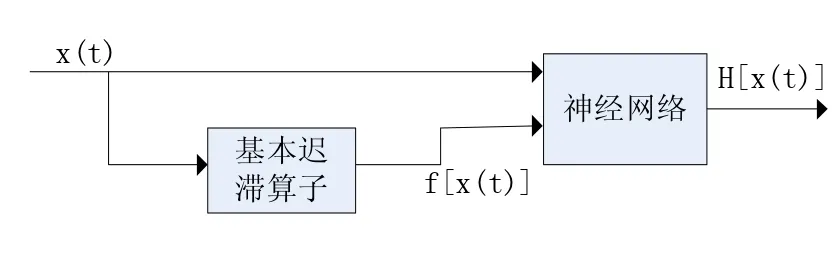
圖2 擴展空間輸入法建立神經網絡

1.3 基本遲滯算子

遲滯的多值映射性是其建模的難點之一。本文以不同閾值play算子作為基本單元構造算子[2-8]。

Play算子定義如下：

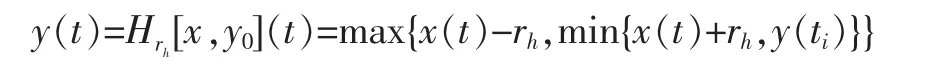
其中rh表示play算子的閾值。

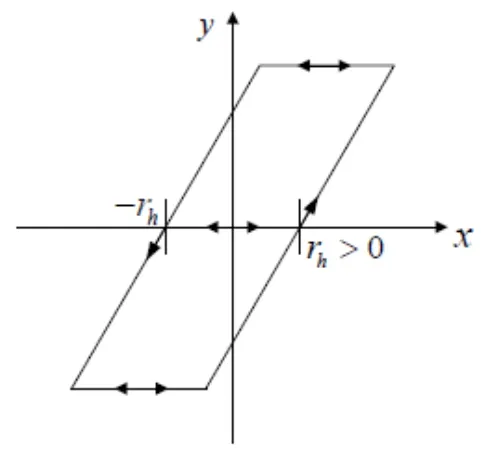
圖3 play算子

PI模型的表達式為：

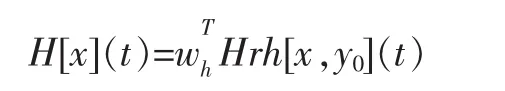
其中wh表示play算子的權重。

算子輸出與執行器輸出使得模型輸入不再是多值，達到一一映射目的。

1.4 ARX模型

自回歸各態歷經模型是一種有理傳遞函數模型，廣泛用于系統的辨識，可用來描述壓電作動器的率相關特性。ARX數學表達式為：

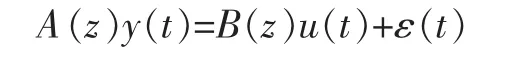
其中ε（t）是誤差項，而：

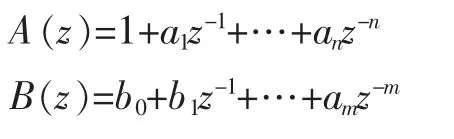
ARX模型傳遞函數為：

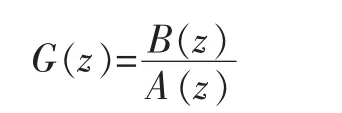
1.5 模型的驗證

以均方根誤差RMSE（Root Mean Square Error）和相對誤差RE（Relative Error）作為檢驗標準[11]，對建模效果進行定量描述，表達式如下：

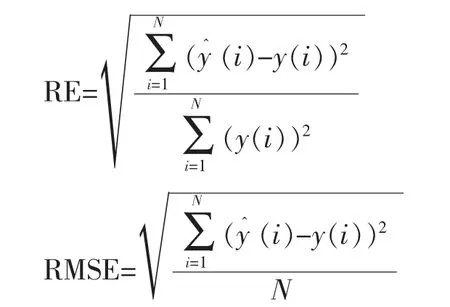
如圖4給出了不同頻率下建模結果與作動器輸出的對比圖。而誤差的RE與RMSE數值見表1。

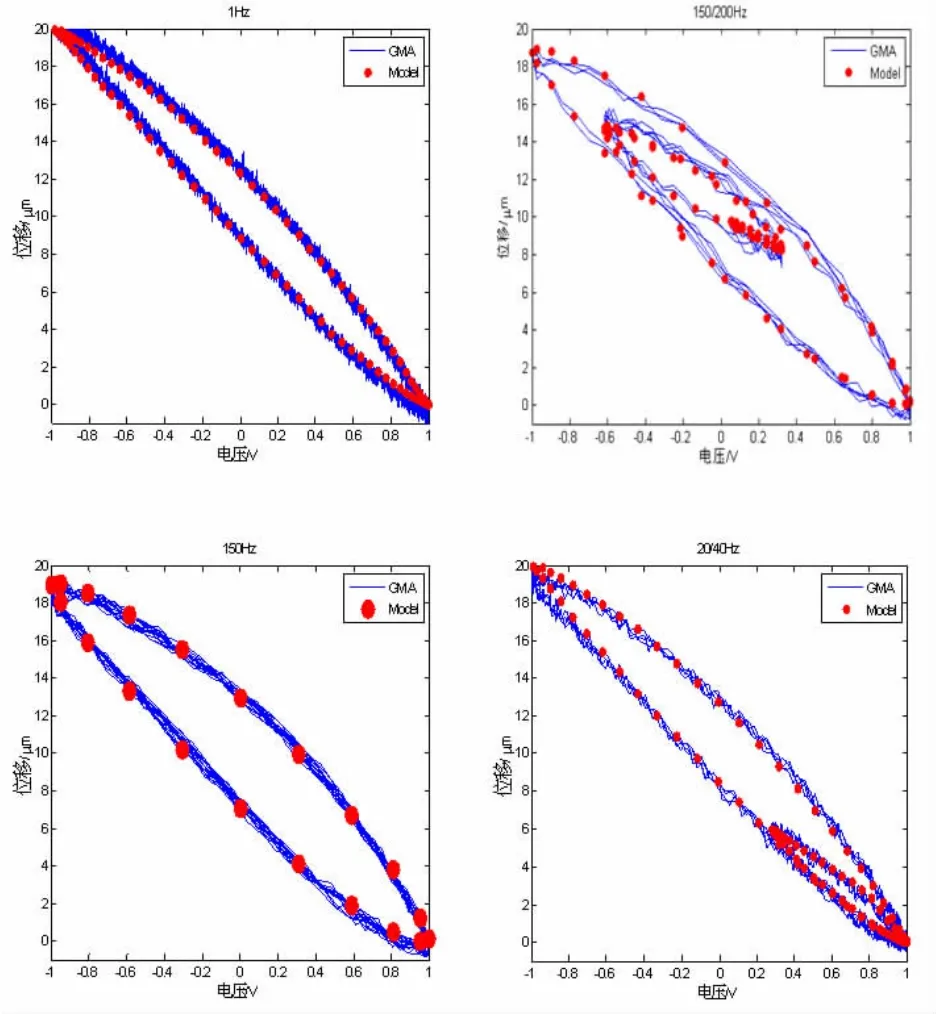
圖4 建模效果驗證

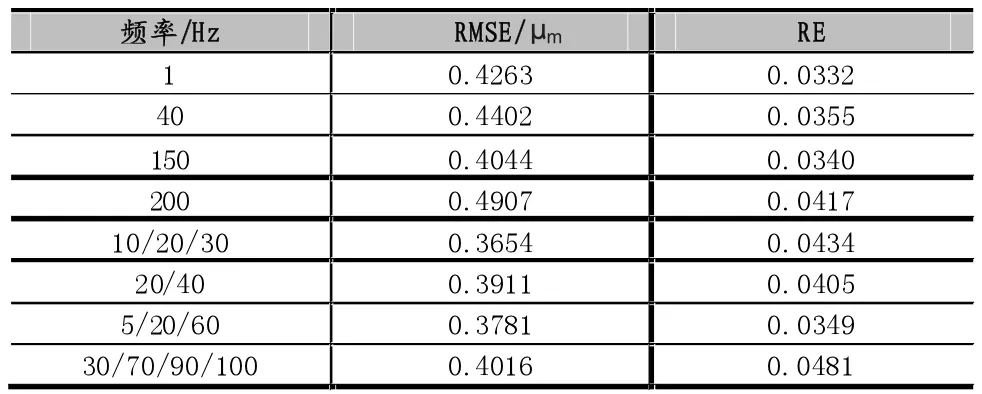
表1 建模驗證誤差

2 跟蹤控制策略及效果

2.1 控制器設計

控制系統結合Hammerstein分為兩部分，以傳統控制方法解決系統本身具有的復雜非線性構成。第一部分逆補償控制，抵消非線性的影響。第二部分PID控制器，彌補開環逆補償控制易受擾動等影響，校正系統的誤差。將兩者結合既可穩定性又可提高跟蹤性能，而且能夠達到實時控制的效果。

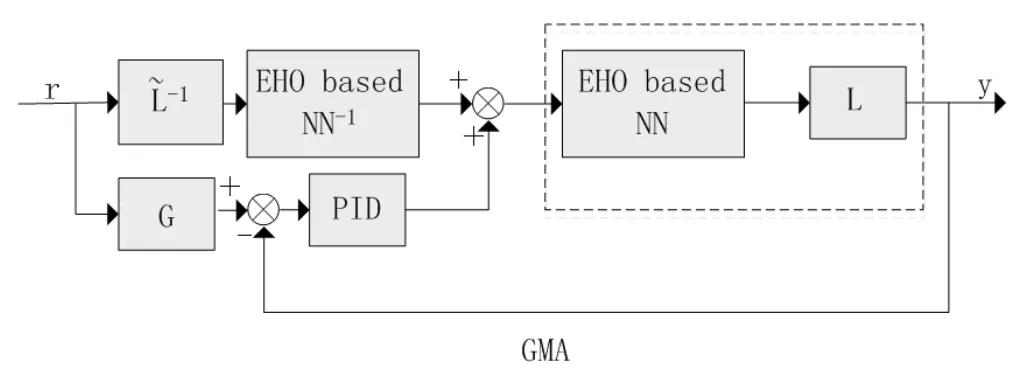
圖5 跟蹤控制器框圖

r和y分別為輸入信號和輸出信號，NN和NN-1為基于基本遲滯算子EHO構建的BP神經網絡模型及其逆模型，L為基于ARX建立的線性動態部分，為線性部分的近似逆，G為前饋補償器。

ARX辨識結果有：

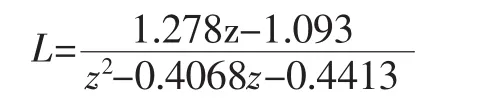
因為L是嚴格正則的，不能直接求逆，取一個近似逆：

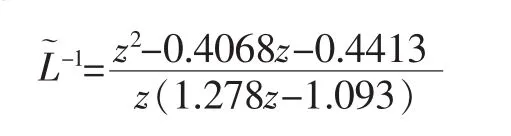
2.2 實時跟蹤控制實驗

實時跟蹤控制實驗，如圖6所示。實驗中所用器材包括半實物仿真平臺dSPACE、上位機、超磁致作動器、GF-20型功率放大器等。首先在上位機中設計好控制程序，下載至dSPACE后，經功率放大器放大后作用于作動器。以電渦流傳感器（靈敏度8mv/μm）測得超磁致作動器的位移信號，回傳給dSPACE，最后在上位機中進行數據分析和處理。

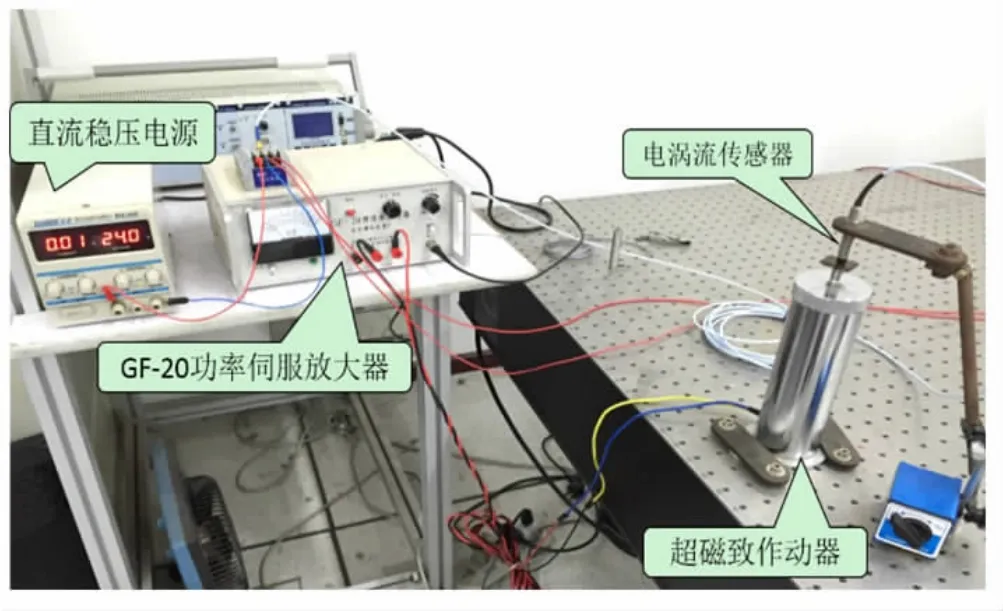
圖6 實時跟蹤實驗

根據設計好的控制策略，使超磁致作動器跟蹤1-200Hz范圍內的參考信號，包括單頻率和復合頻率。

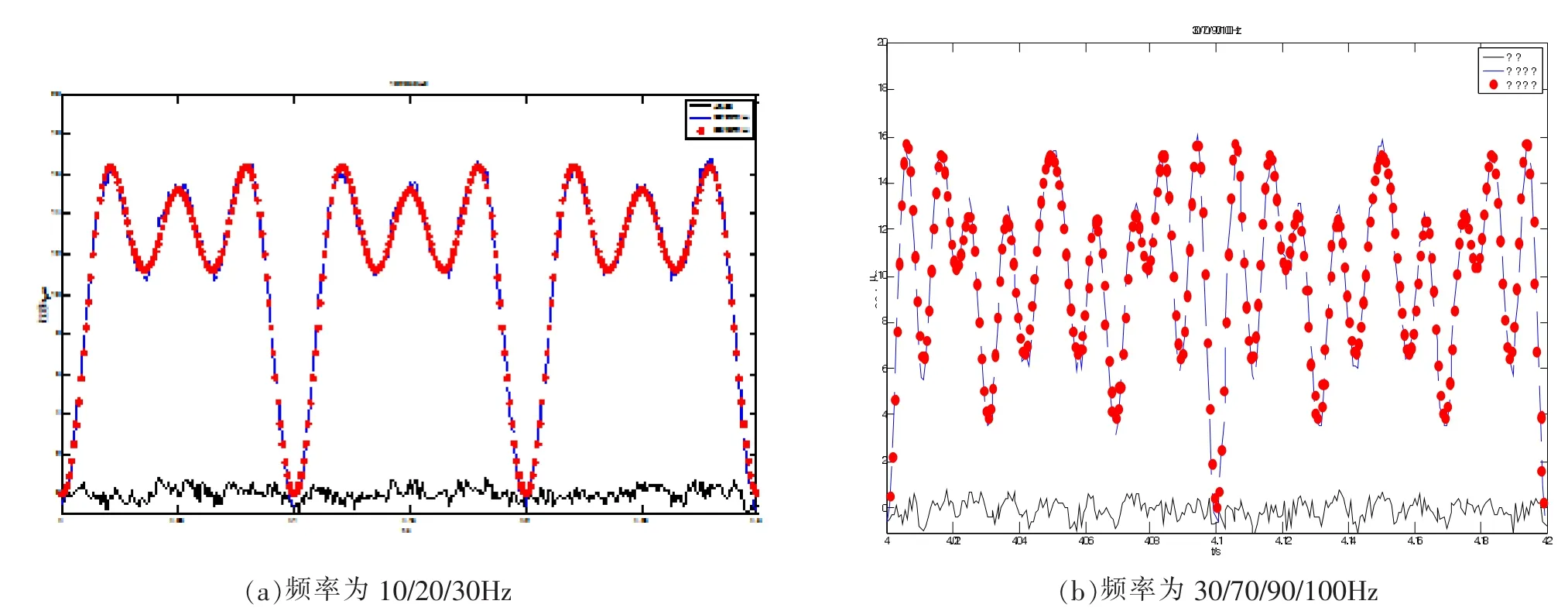
圖7給出了幾組跟蹤效果對比圖，表2詳細給出了多種頻率輸入信號跟蹤控制的均方根誤差和相對誤差。

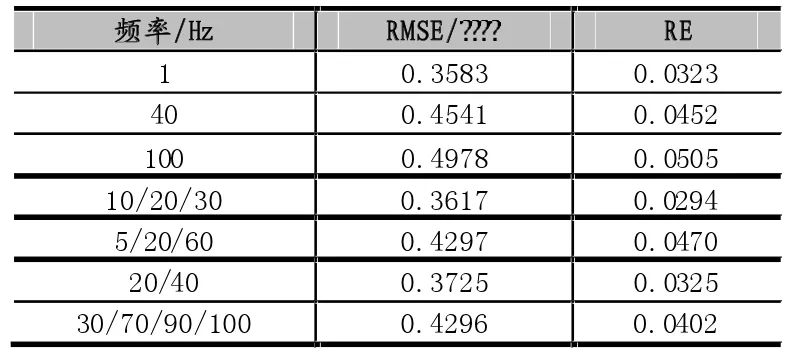
表2 跟蹤控制誤差

3 結語

本文以超磁致作動器（GMA）為研究對象，基于BP神經網絡建立了0-200Hz內的Hammerstein模型[1]，并基于此模型設計了逆補償結合PID控制的跟蹤控制器。實驗結果顯示，該模型和控制器對單頻和復合頻率的輸入信號都適用。實時跟蹤實驗驗證了上述模型，能夠有效跟蹤不同頻率，包括復合頻率的信號。控制效果的均方根誤差小于0.5μm，相對誤差小于4.7%。

[1]毛劍琴.智能結構動力學與控制[M].科學出版社，2013.

[2]谷國迎.壓電陶瓷驅動微位移平臺的磁滯補償控制理論和方法研究[D].上海交通大學，2012.

[3]Knohl T，Unbehauen H.Adaptive Position Control of Electrohydraulic Servo Systems Using ANN[J].Mechatronics，2000，10（1-2）: 127-143.

[4]柳萍，毛劍琴，張偉，等.基于Hammerstein-like模型的超磁致伸縮作動器建模與控制[J].北京航空航天大學學報，2013，39（7）：17-921.

[5]毛劍琴，岳玉芳，張建剛，等.復雜系統模糊建模的模糊樹方法[J].控制理論與應用，2002，19（2）:153-156.

[6]Tao G，Kokotovic P V.Adaptive Control of Plants with Unknown Hysteresis[J].IEEE Transactions on Automatic Control，1995，40（2）：200-212.

[7]Liu J，Zhou K.Neural Networks Based Modeling and Robust Control of Hysteresis[C]Control Conference（CCC），2016 35th Chinese. TCCT，2016:3051-3056.

[8]Giri F.Block-Oriented Nonlinear System Identification[M].Berlin:Springer，2010.

[9]Zhao X，Tan Y.Modeling Hysteresis and Its Inverse Model Using Neural Networks Based on Expanded Input Space Method[J].IEEE Transactions on Control Systems Technology，2008，16（3）:484-490.

[10]Kuhnen K.Modeling，Identification and Compensation of Complex Hysteretic Nonlinearities:A Modified Prandtl-Ishlinskii Approach [J].European journal of control，2003，9（4）:407-418.

[11]范家華，周攀，郝兵兵，等.基于BP神經網絡的壓電作動器建模與控制[J].現代計算機，2016（8）:35-39.

Modeling and Control of Giant Magnetostrictive Actuators Based on BP Neural Network

WANG Dan-mei，FENG Wei-feng
（College of Electrical Engineering，Southwest Jiaotong University，Chengdu 611756）

The hysteresis nonlinearity of the GMA is a major obstacle in the application of such material in actuators.Establishes a Hammerstein model based on the BP neural network to model the hysteresis nonlinearity.Based on the model,designs a composite control strategy combining feed-forward compensation and PID feedback control.The controller ensures tracking control for all single and complex frequency input signals within the modeling range.Finally,the results of the real-time tracking experiment on GMA further validate the modeling and control results.

Hysteresis Nonlinearity;Giant Magnetostrictive Actuators;BP Neural Network;Hammerstein Model

國家自然科學基金重點項目（No.61433011）

1007-1423（2017）09-0011-05

10.3969/j.issn.1007-1423.2017.09.003

王丹梅（1992-），女，四川資陽人，碩士研究生，研究方向為遲滯非線性系統建模與控制

2017-02-17

2017-03-10

馮偉峰（1991-），男，廣東佛山人，碩士研究生，研究方向為機器人控制