復雜網絡中重要節點的發現

姜勝文

（四川大學計算機學院，成都 610065）

復雜網絡中重要節點的發現

姜勝文

（四川大學計算機學院，成都 610065）

復雜網絡中重要節點的發現在實際應用中有著重要意義。重要節點的發現依賴于節點的重要性評估，而如今的一些節點重要性評估參數如介數、度分布、聚類系數等存在適用范圍有限、評估結果不夠全面等局限性，因為節點在復雜網絡中的重要性程度不僅僅只受單一因素的影響。提出一種基于拉普拉斯特征映射算法的節點重要性綜合評估方法。這種方法能綜合考慮全部節點的局部特征，可以準確地對節點在復雜網絡中的重要性程度進行評估，同時能夠得到良好的結果。由于該方法無需對復雜網絡中所有節點的全部特征進行評估，極大地縮減計算時間，在保證精確性的同時，提高效率，并通過MATLAB仿真與現有算法的結果進行分析對比，證明該算法的有效性和可行性。

復雜網絡；重要節點；拉普拉斯特征映射

0 引言

復雜網絡的各項基礎研究工作中，節點的重要程度評估，重要節點的發掘，具有重要的理論與應用價值[1-2]。國內外在復雜網絡重要節點發現研究領域已有諸多成果，對節點的重要性評估方法也有很多，其本質均是源于圖論和基于圖的數據挖掘，對應于圖論中的最關鍵的節點問題和最關鍵邊問題[3-4]。一般可以通過復雜網絡中節點的中心性指標衡量節點的重要性程度，人們經常使用的復雜網絡中心性評估指標有介數中心性、特征向量中心性、度中心性、接近中心性等。這些評估指標分別從不同角度描述了每個節點在網絡中的重要性程度[5-7]。但現實世界中的復雜網絡千變萬化、錯綜復雜，很難只從單一評估指標來評估某個節點在復雜網絡中的重要性程度，由于單一指標在不同的網絡拓撲結構上的評估具有很大的片面性，復雜網絡中每個節點的重要性和這個網絡的整體結構相關，需要從多個角度，利用節點的多個重要性指標來進行綜合評估[8]。因此本文提出了基于拉普拉斯特征映射算法利用節點的多個指標來進行綜合評估，以確定其在復雜網絡中的重要程度。因為衡量節點的多個重要性指標對節點進行綜合評估能夠涵蓋影響節點重要性的多種因素，也不再是片面強調某種單一指標的影響，因此能夠得到比使用單一指標評估更為精準的節點重要性評估結果。利用該方法對大家普遍使用的 “ARPA網絡”數據集的仿真結果表明，此方法能夠有效評估與發現復雜網絡中的重要節點。

1 拉普拉斯特征映射算法介紹

1.1 算法描述

復雜網絡中的節點重要性發現是復雜網絡研究各領域的一個基本課題,本節從特征映射角度出發,介紹了一種基于流形學習思想的節點重要性評估算法，即拉普拉斯特征映射算法（Laplacian Eigenmaps，LE）。拉普拉斯特征映射算法[9]是一種非線性降維方法，它將原始數據集映射到低維空間，映射關系分別是X∈Rm×N與Y∈Rd×N，其中m是原始特征維數，d是新特征維數（d〈m），N是數據集的樣本個數，原始數據集與映射集中的樣本分別是xi∈Rm和yi∈Rd。拉普拉斯特征映射是基于局部保序，能夠找到一種映射方式X-〉Y，同時也能保持數據集中的數據在特征空間分布的局部幾何屬性。它的主要思想是，如果兩個數據實例Xi和Xj很相似，那么它們在降維后的目標子空間中應該盡量接近。對于高維空間的點構建連通的無向加權圖，再通過求解圖拉普拉斯算子的廣義特征值實現映射[10]。該算法首先在數據圖形中構建 Laplace-Bel-trsmi算子，然后從與 Laplace-Beltrsmi算子相一致的幾個最小特征值的特征向量中得出降維后的低維數據集[11]。

1.2 拉普拉斯特征映射算法流程

步驟1構建圖 確定每個Xi∈Rm的近鄰，并構建鄰域關系圖G（V，E），如采用KNN算法。

步驟2確定權值

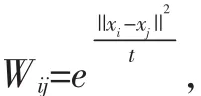
（2）簡單方法：在圖G（V,E）中，若數據點Xi與Xj相連接，則權重設定為Wij=1，否則，Wij=0。

步驟3特征映射 尋找關系映射Ψ：G（V，E）→Y= {y1，y2，…，Yn-1，yN}?Rd，即將鄰域加權圖 G（V，E）的節點映射為低維歐氏空間Rd中的一組像點Y={y1，y2，…，Yn-1，yN}，然后定義最小化目標函數：

矩陣L叫作圖的拉普拉斯矩陣，優化問題則可以寫成更簡潔的形式：

2 仿真實驗

2.1 實驗條件與方法

利用大家普遍使用的“APRA網絡”拓撲結構[12]（如圖1）來分析驗證基于拉普拉斯特征映射算法的網絡節點重要性多指標多維度的評估方法的正確性。該“APRA網絡”拓撲結構為北美常用干線拓撲結構，它由21個節點與26條邊組成，根據網絡拓撲可得各節點指標數據如下（表1）：

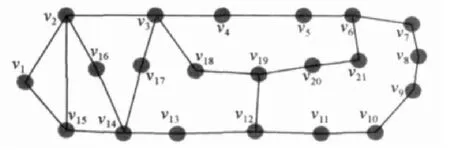
圖1 “APRA網絡”拓撲

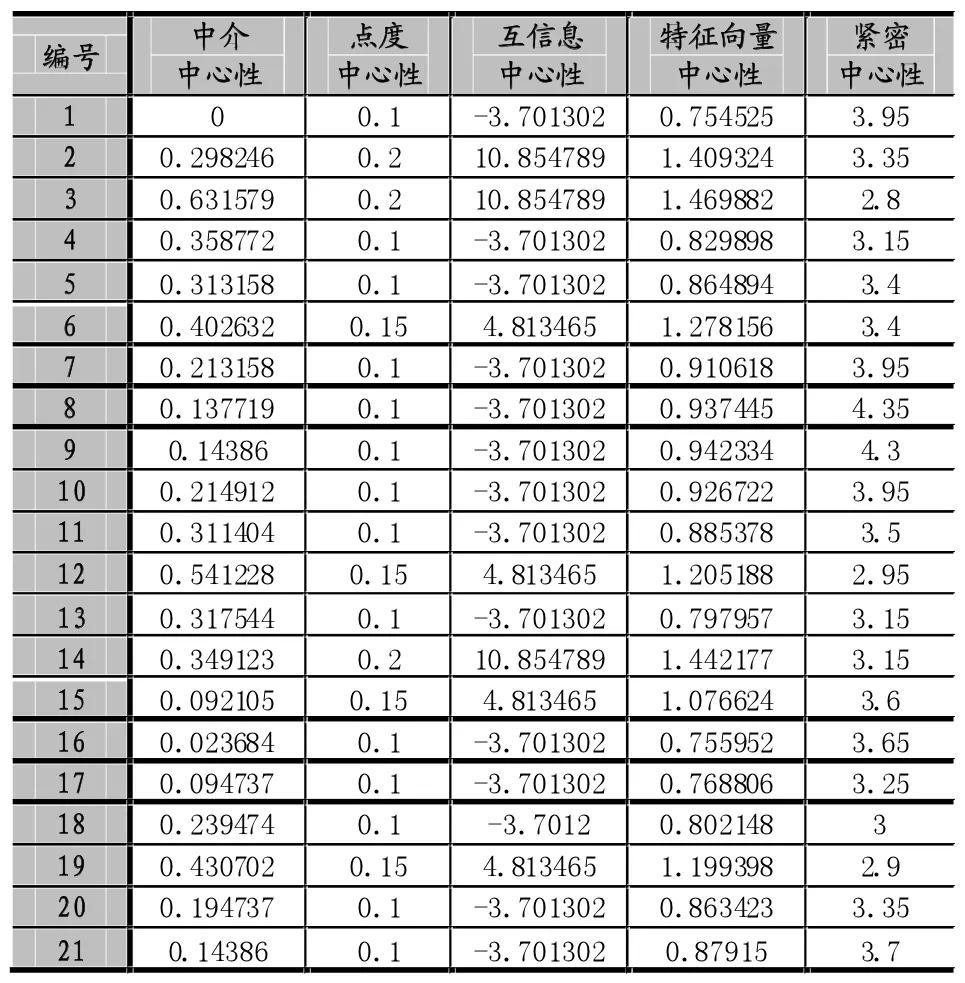
表1 “ARPA網絡”各節點的相關指標數據

2.2 實驗結果及分析

根據上一節介紹的拉普拉斯特征映射算法，可以計算得出APRA網絡中各個節點的得分情況。圖2是APRA網各節點相應指標折線對比 （為了更清晰地觀察結果，故將相應指標放在兩張圖里面）。

由圖2可以看出，本文介紹的拉普拉斯特征映射算法得到的最重要節點為v3，同時另幾種方法得到的結果也為v3（互信息中心性方法與點度中心性中v3和v2得分一樣，認為它們在網絡中的重要性是相同的），而除了v3之外，拉普拉斯算法認為剩下節點中最重要的5個節點為14，2，19，12，6，而其他幾種方法得出的結果也為14，2，12，6，19，說明拉普拉斯算法的結果和其他幾種方法的結果是一致的。下面再來看一下拉普拉斯算法與普遍公認的PCA與LDA算法進行對比分析。

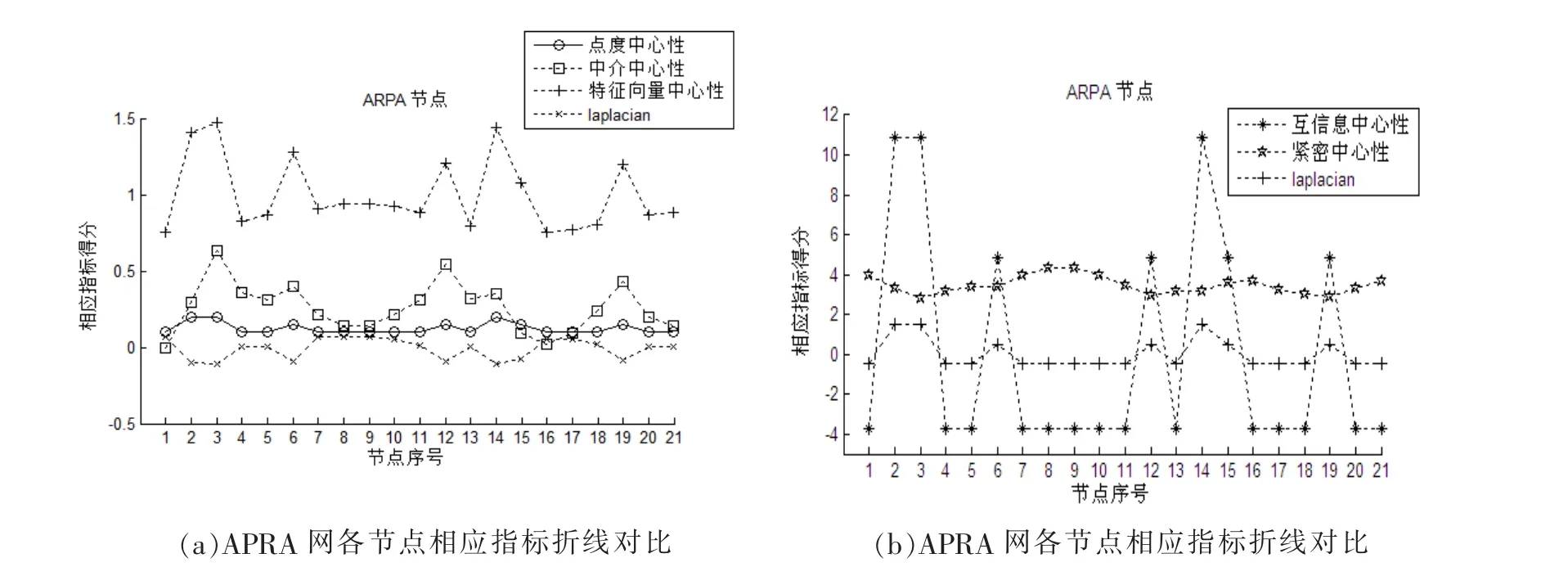
圖2

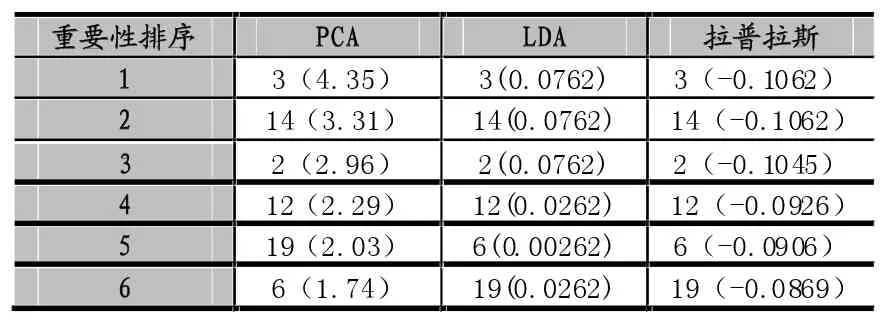
表2 APRA網絡三種算法結果對照（前面數值為節點序號，括號內為相對應指標得分）

由表2仍然可以看出，PCA （主成分分析法）和LDA（線性判別分析）以及拉普拉斯算法都認為v3為APRA網絡中最重要的節點，其次為v14，v2。同時我們可以觀測v19、v12、v16這三個節點，這些節點的LDA得分與點度中心性評分相同，可以認為這三個節點的重要性相同，而根據中介中心性評分指標，認為網絡中有更多的節點通過v12這個節點和其他節點進行通信，另外互信息中心性則認為網絡中有更多的節點和v6進行通信，較少節點與v19通信；而特征向量中心性認為v6在網絡中更受v5、v7、v8、v9這些節點歡迎，因為它們都需要通過v6與網絡中其他的節點進行通信。本文提出的復雜網絡中重要節點的評估方法綜合考慮了以上所有指標，經過客觀分析，最終認為v12節點優于v6節點優于v19節點。因此，本文算法結果與其他算法基本一致且更細致合理。由此可見，本文提出的拉普拉斯特征映射方法完全可以用來找出復雜網絡中位置重要的節點，并且具有很好的參考價值。

3 結語

節點在復雜網絡中的重要程度不應該僅用單一指標來衡量，而需要從多個角度和方面，充分利用節點的多個評估指標來進行綜合評估與分析。本文提出了基于拉普拉斯特征映射算法評估復雜網絡中節點重要性的方法，此方法綜合考慮了每個節點的局部特征，可以準確地對節點在網絡中的重要程度進行評估，得到了良好的結果。由于只需對網絡中的每個節點的局部屬性進行評估，大大縮減了計算時間，在保證精確性的同時，提高了效率。該方法在 “ARPA網絡”的仿真實驗中，驗證了它的可行性與有效性，為進一步分析復雜網絡中重要節點的性質，并有效地加以利用奠定了基礎。

[1]HE Nan，LI De-Yi，GAN Wen-Yan，ZHU Xi.Mining Vital Nodes in Complex Networks.Computer Science，2007，34（12）:15-16.

[2]張翼.復雜網絡節點重要性評估及其應用研究.計算機科學，2011，5:26-28

[3]許進.一種研究系統的新方法-核與核度法[J].系統工程與電子技術，1994（6）:1-10.

[4]P Onnela J，Saramaki J，Kertesz K，Kaski.Intensity and Coherence of Motifs in Weighted Complex Networks[J].Phys Rev.2005.9:34-36.

[5]李鵬翔，任玉晴，席酉民.網絡節點（集）重要性的一種度量指標.系統工程，2004，12:56-59.

[6]譚躍進，鄧宏鐘.復雜網絡中節點重要度評估的節點收縮方法[J].系統工程理論與實踐，2006（11）:79-105.

[7]王延慶.基于接連失效的復雜網絡節點重要性評估[J].網絡安全技術與應用，2008（3）:59-61.

[8]于會，劉尊，李勇軍.基于多屬性決策的復雜網絡節點重要性綜合評價方法[J].物理學報，2013（2）:54-62.

[9]Belkin M，Niyogi P.Laplacian Eigenmaps and Spectral Techniques for Embedding and Clustering.Advances in Neural Information Processing Systems，2002：1585-592.

[10]姜偉，楊炳儒.基于流形學習的維數約簡算法[J].計算機工程，2010（12）:25-27.

[11]畢達天，邱長波，張晗.數據降維技術研究現狀及其進展.情報理論與實踐，2013，36（2）:125-126.

[12]晉建志.復雜網絡基于節點重要性的社團探測及社團演化模型研究.華中師范大學博士論文，2014.5.

Discovery for Important Nodes of Complex Networks

JIANG Sheng-wen
（College of Computer Science，Sichuan University，Chengdu 610065）

In complex networks,it is important how to evaluate the nodes according to their importance.Discovering the important nodes depends on the importance evaluation of nodes.Nowadays most of the existing methods of evaluating pivotal nodes(e.g.betweenness-based,degree distribution,clustering efficient)only think about one factor but not the integration of all complex network in evaluating the importance of nodes,so this methods each can do work in limited application scope.Proposes Laplacian Eigenmaps algorithm to discover the vital nodes in complex networks.In this algorithm,ranking key nodes will consider each node′s integration of whole complex network.After that,it can be accurate to evaluate important degree of the node in the network,and can get a good result.Due to the evaluation does not need calculate whole attribute of complex networks′nodes,so it can greatly reduce the computing time,and the efficiency to discover the key nodes can be improved.Finally,the experiment′s result of MATLAB simulation about the proposed algorithm shows that this algorithm is feasible and effective.

Complex Networks;Key Nodes;Laplacian Eigenmaps

1007-1423（2017）09-0007-05

10.3969/j.issn.1007-1423.2017.09.002

姜勝文（1990-），男，湖北黃岡人，碩士研究生，研究方向為網絡與信息安全

2017-02-23

2017-03-15