滾動阻力對車輛運動穩(wěn)定性的影響分析?

李 玲，施樹明，王憲彬，張向東

(1.吉林大學交通學院，長春 130022； 2.東北林業(yè)大學交通學院，哈爾濱 150040)

滾動阻力對車輛運動穩(wěn)定性的影響分析?

李 玲1，施樹明1，王憲彬2，張向東1

(1.吉林大學交通學院，長春 130022； 2.東北林業(yè)大學交通學院，哈爾濱 150040)

鑒于傳統(tǒng)的以經(jīng)典線性2自由度模型為基礎的多自由度非線性車輛系統(tǒng)模型中通常忽略輪胎滾動阻力的影響而難以反映車輛運動的真實狀態(tài)，本文中在發(fā)動機制動工況下，建立計及輪胎滾動阻力的5自由度(縱向速度、側向速度、橫擺角速度和前后輪轉動速度)車輛模型，利用非線性系統(tǒng)的全局相平面和狀態(tài)變量時間序列等分析方法研究了滾動阻力對高速轉向行駛車輛動力學特征的影響。仿真結果表明，在發(fā)動機制動工況下，車速逐漸降低的過程中，滾動阻力嚴重影響車輛系統(tǒng)的運動狀態(tài)。因此，建立包含滾動阻力的車輛模型有利于分析汽車的操縱穩(wěn)定性特征，為實驗驗證理論模型的正確性提供理論支持。

操縱穩(wěn)定性；輪胎滾動阻力；車輛動力學；失穩(wěn)運動

前言

高速行駛的車輛，為避讓障礙物，在緊急轉向過程中，利用發(fā)動機進行減速制動時，會引起車輛系統(tǒng)的失穩(wěn)運動[1]。利用現(xiàn)有的車輛模型[2]，在發(fā)動機制動工況下，對高速轉向車輛失穩(wěn)運動進行仿真分析時發(fā)現(xiàn)，車輛系統(tǒng)在失穩(wěn)后的很長時間內不能停止運動。但前期的模型車實驗研究表明，在發(fā)動機制動工況下，無論車輛是否失穩(wěn)，高速轉向車輛在一定時間內都能夠很快停止運動。這種理論與實際實驗的差異性說明，現(xiàn)有的車輛操縱穩(wěn)定性分析模型不能準確地描述發(fā)動機制動工況下車輛系統(tǒng)的動力學特征，還存在被忽略的重要影響因素。初步分析認為，這種差異性是由于車輛模型中沒有考慮輪胎滾動阻力的影響。

目前，在車輛模型建立方面，以2自由度汽車動力學模型為基礎的汽車轉向穩(wěn)定性研究已經(jīng)取得較豐碩的研究成果[3－5]。文獻[6]中利用2自由度汽車模型和非線性輪胎模型分析了汽車在轉彎過程中的穩(wěn)態(tài)動力學分岔特征。文獻[7]中為評價汽車安全輔助駕駛系統(tǒng)的有效性，將縱向速度作為一個自由度引入到模型中，提出了一種基于3自由度模型駕駛穩(wěn)定區(qū)域的計算方法。文獻[2]中在3自由度模型的基礎上，引入驅動建立了車輛系統(tǒng)5自由度模型，揭示了驅動對汽車操縱穩(wěn)定性的影響。這些車輛操縱穩(wěn)定性模型都關注于高速時車輛的運動狀態(tài)，沒有考慮輪胎滾動阻力的影響。但是在車速逐漸降低的過程中，輪胎滾動阻力對車輛系統(tǒng)運動特征的影響很大，不可忽略。

輪胎在路面上滾動時，滾動阻力使機械能轉變?yōu)闊崮堋Ｊ聦嵣希喬ハ牧税l(fā)動機傳遞給車輪的部分能量，利用剩余的能量驅動車輛前進[8]。目前，滾動阻力在縱向車輛動力學中已經(jīng)得到比較完善的研究和表達。文獻[9]和文獻[10]中指出，作用于車輛系統(tǒng)的外力包括輪胎力、滾動阻力和空氣阻力。汽車除了克服來自空氣的阻力之外，還必須克服來自地面的滾動阻力。滾動阻力的引入是由于輪胎變形產(chǎn)生的遲滯損失[11]。作用在驅動輪上的轉矩必須克服滾動阻力矩的作用，剩余部分才能用于形成輪胎與路面之間的作用力[12－13]。但車輛操縱穩(wěn)定性非線性動力學研究中，在分析車輛系統(tǒng)動力學特征時通常忽略滾動阻力的影響。

文獻[14]和文獻[15]中在提出魔術公式時指出，為允許曲線相對于原點(x－o－y)有一個偏移量，引入兩個移動因子Sh和Sv，滾動阻力使輪胎力的偏移量增加，即考慮滾動阻力的魔術公式曲線坐標系為X－o－Y。但通常使用的魔術公式中不考慮滾動阻力的影響，直接采用x－o－y坐標系中過原點的曲線計算輪胎力。文獻[12]中在描述地面附著率時給出了附著率的表達式，同時強調車輛在道路上運行時，滾動阻力總是很小，可以忽略不計，從而得到不考慮滾動阻力的附著率和滑移率曲線。但根據(jù)文獻[16]中關于風阻和滾動阻力的比重圖描述中可以看到，在車速逐漸降低的過程中滾動阻力比重逐漸增大，最高可達到80%以上，因此，在研究低速運動狀態(tài)時，滾動阻力是一個不可或缺的因素。

本文中在所建立的針對發(fā)動機制動工況的車輛系統(tǒng)5自由度非線性模型的基礎上，引入滾動阻力，建立包含滾動阻力的車輛系統(tǒng)5自由度非線性模型，利用相平面和狀態(tài)變量時間序列等方法，分析高速轉彎行駛車輛在發(fā)動機制動作用下減速的過程中，輪胎滾動阻力對系統(tǒng)動力學特征的影響。

1 建立車輛系統(tǒng)模型

高速行駛的車輛在轉彎時，針對利用發(fā)動機制動使車輛減速轉彎的情況，基于發(fā)動機制動工況下的5自由度平面運動非線性車輛系統(tǒng)方程[17]，在對該工況下的滾動阻力進行具體分析的基礎上，建立發(fā)動機制動下包含滾動阻力的5自由度非線性車輛模型。

1.1 包含滾動阻力的車輛系統(tǒng)模型

在已有的針對發(fā)動機制動工況的5自由度車輛系統(tǒng)模型的基礎上，引入前后輪輪胎滾動阻力，建立考慮滾動阻力的車輛系統(tǒng)模型。

1.1.1 滾動阻力的計算

當輪胎在路面上轉動時，與路面接觸的輪胎圓周部分產(chǎn)生變形。消耗在變形上的一部分能量在輪胎恢復變形的過程中將無法恢復。因此，在接觸區(qū)域內壓力分布的變化使得印跡前端的應力比后端更高。該過程中能量的消耗和壓力變形產(chǎn)生滾動阻力，該力的方向與輪胎運動方向相反且與輪胎印跡內的載荷成正比[18]:

式中:ωw為車輪角速度；Fz為輪胎垂直載荷；μr為滾動摩擦因數(shù)。μr不是恒定的，它主要依賴于輪胎的速度、充氣壓力、側偏角及外傾角。它也取決于機械性能、速度、磨損、溫度、負載、尺寸及道路狀況。本文中取μr＝0.015＋7×10－6v2，v為車速[19]。

由式(1)可計算得到作用在前后輪上的滾動阻力Frf和Frr:

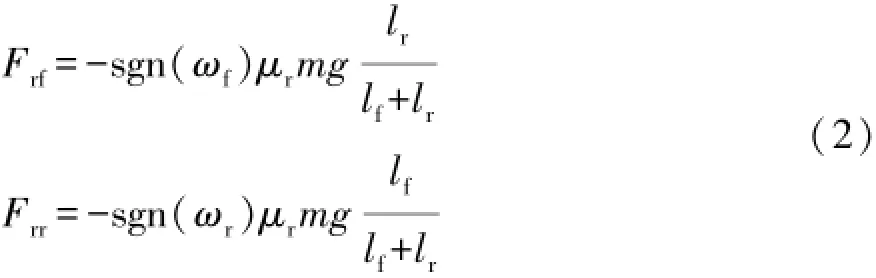
式中:m為整車質量；ωf為前輪角速度；ωr為后輪角速度；lf為前軸距；lr為后軸距。

當前輪轉動時，會在輪胎上產(chǎn)生一個側偏角，圖1所示為作用于前輪的滾動阻力分析圖。為建立考慮滾動阻力的整車5自由度非線性模型，需要將輪胎上的滾動阻力沿輪胎縱向和側向即沿x－y軸分解，故如圖1所示，將前輪滾動阻力分解為沿x方向的輪胎縱向滾阻Frfcos(－αf)和沿y軸方向的輪胎側向滾阻Frfsin(－αf)。這里輪胎側偏角取負號是由于魔術公式中規(guī)定的輪胎側偏角正方向與輪胎側偏角實際作用的正方向相反。

1.1.2 滾動阻力的施加方式

當車輪側偏時，在輪胎的縱向和側向同時作用有滾動阻力。驅動力矩必須克服滾動阻力，剩余部分才用于車輛前進運動[12]。即輪胎必須首先克服滾動阻力產(chǎn)生的遲滯損失，才能進一步形成輪胎與路面之間的作用力。因此，本文中縱向滾動阻力以滾動阻力矩的方式施加給前后輪，側向滾動阻力直接施加在車輪側向。

圖2為前輪輪胎轉動動力學分析圖，結合圖1可得前輪滾動阻力矩Txf為其中，輪胎與路面間產(chǎn)生的作用力Fbf為

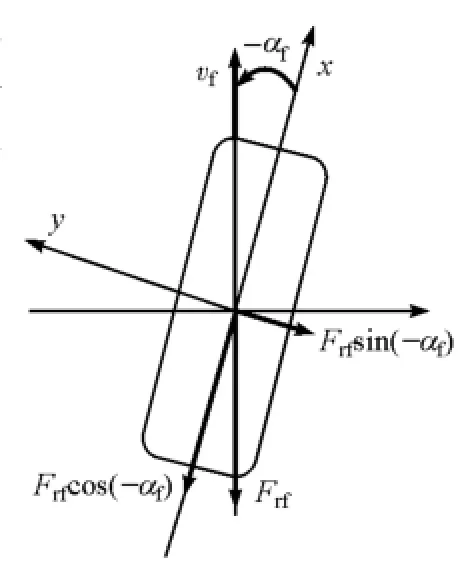
圖1 前輪滾動阻力分析圖

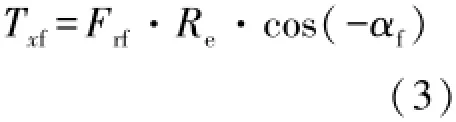
同理可得后輪滾動阻力矩Txr為

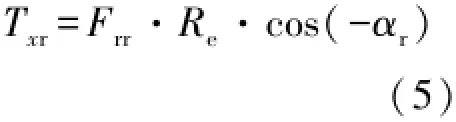
前后輪側向滾動阻力Fryf和Fryr為

式中:Re為車輪轉動半徑；αf和αr為前后輪側偏角。1.1.3 考慮滾動阻力的車輛系統(tǒng)模型

根據(jù)1.1.2節(jié)對前后輪滾動阻力的分析，采用圖3所示的考慮滾動阻力的單軌車輛模型，與文獻[17]中不包含滾動阻力的車輛模型相比，該模型一方面在前后輪輪胎縱向施加滾動阻力矩(如圖2)，另一方面在前后輪輪胎側向施加側向滾動阻力。因此，建立包含滾動阻力的前輪轉向車輛系統(tǒng)5自由度非線性模型:

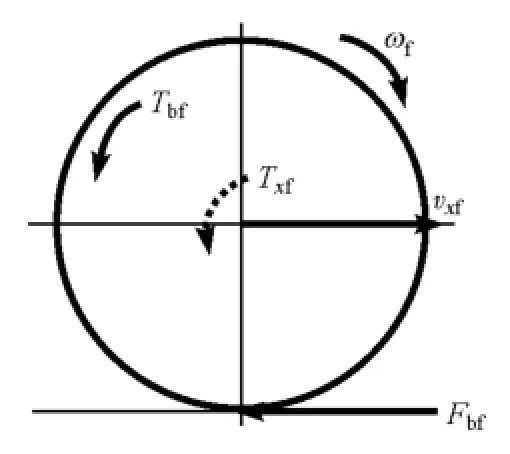
圖2 前輪轉動動力學分析

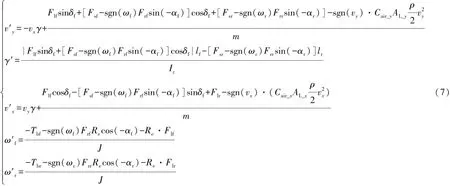
式中:Iz為繞z軸的轉動慣量；vx為縱向速度；vy為側向速度；γ為橫擺角速度；J為車輪轉動慣量；δf為前輪轉角；Cair＿x和Cair＿y為縱向和側向風阻系數(shù)；AL＿x和AL＿y為縱向和側向迎風面積；ρ為空氣密度；Tbf和Tbr為前后輪制動力矩；Flf，F(xiàn)lr，F(xiàn)sf和Fsr為前后輪縱向和側向輪胎力。具體的車輛參數(shù)見表1。

1.2 輪胎模型

穩(wěn)態(tài)輪胎力的計算方法采用經(jīng)典的魔術公式[20]:

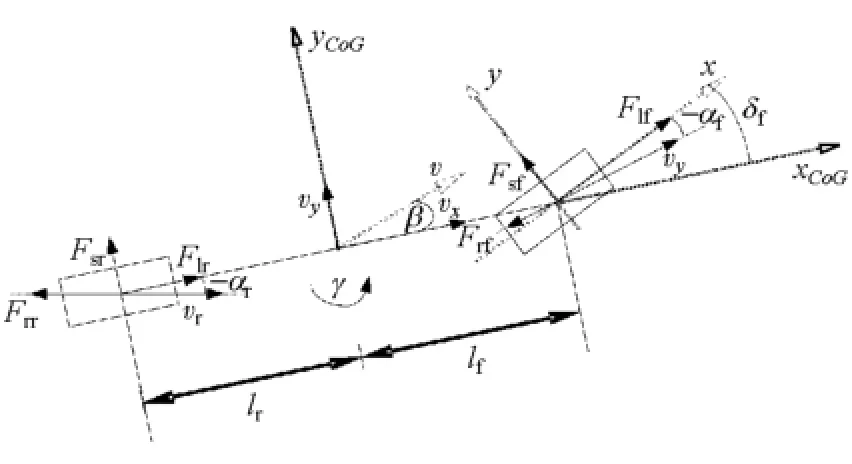
圖3 考慮滾動阻力的單軌車輛模型

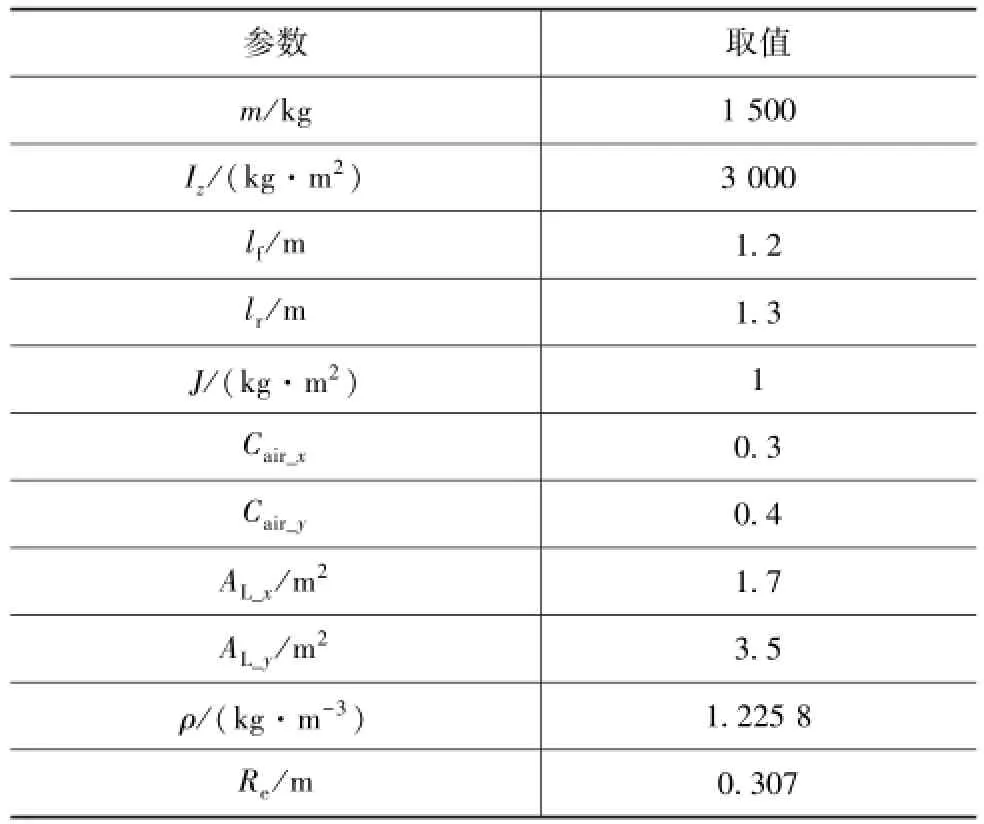
表1 汽車參數(shù)

F＝Dsin(Carctan(Bx－E(Bx－arctanBx)))(8)式中:B，C，D和E為參數(shù)，參數(shù)值見表2；F為輪胎縱向力或側向力；x為輪胎滑移率或側偏角。

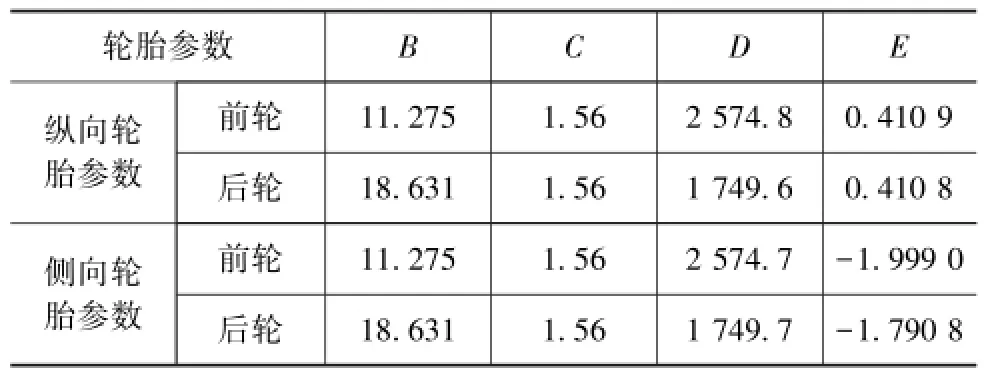
表2 縱向與側向輪胎力參數(shù)

為便于計算機分析，滑移率方程為

前后輪的輪胎側偏角的表達式分別為

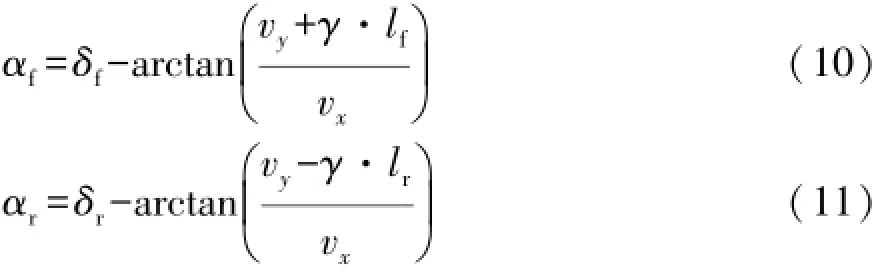
對于輪胎混合滑移，采用Pacejka提出的模型進行分析，具體計算公式為x式中:vwx為輪心處的縱向速度；后輪轉角δr＝0；Flf0，F(xiàn)lr0，F(xiàn)sf0和Fsr0為穩(wěn)態(tài)下前后車輪縱向力和側向力，其大小可以用式(8)計算；Gx和Gy為輪胎力混合滑移修正函數(shù)；rx，1，rx，2，ry，1和ry，2為輪胎力混合滑移修正系數(shù)，見表3。

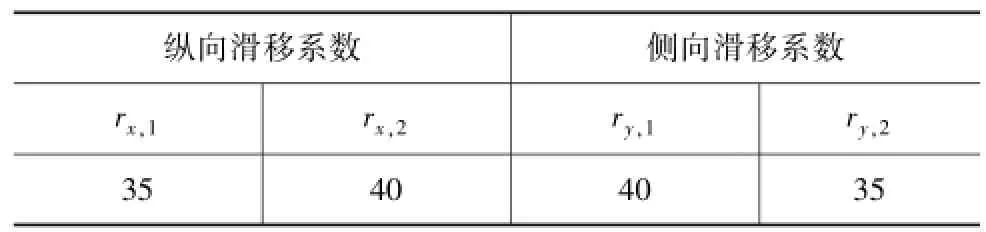
表3 混合滑移系數(shù)

1.3 車輛系統(tǒng)輸入

車輛系統(tǒng)的輸入量包括車輪轉角和反拖力矩。本文中車輛系統(tǒng)為前輪驅動前輪轉向系統(tǒng)，前輪轉角的輸入采用正弦輸入形式:

式中:A為前輪轉角幅值；f為前輪轉角變化的頻率。

根據(jù)經(jīng)驗公式，采用等距取點擬合的方法，得到發(fā)動機制動工況下，作用在驅動輪上的制動力矩的擬合計算式[17]:

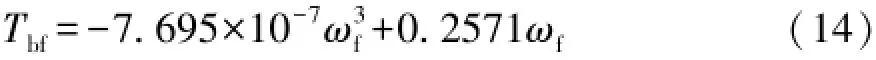
1.4 空氣阻力

模型中引入符號函數(shù)(sgn)來描述空氣阻力。在汽車失穩(wěn)過程中，行駛方向有前后左右多種情況，空氣阻力的方向始終與行駛方向相反，所以要獲得速度的符號，并通過負號給車輛施加與行駛方向相反的空氣阻力。

2 車輛系統(tǒng)模型的仿真分析

由于在發(fā)動機制動工況下開展車輛高速轉向實驗，危險性較大，本文中采用數(shù)值仿真分析方法對是否考慮滾動阻力的車輛模型進行仿真驗證，對比分析滾動阻力對車輛系統(tǒng)運動特征的影響。

2.1 不考慮滾動阻力的車輛系統(tǒng)仿真

取前輪轉角變化的頻率f＝0.4Hz，幅值A＝0.04，單初值點的側向速度vy＝0，橫擺角速度ω＝0，縱向初速度vx＝20m/s。在發(fā)動機制動工況下，采用不包含滾動阻力的車輛模型進行仿真分析。圖4～圖7為車輛系統(tǒng)模型仿真200s的時間內得到的結果。

圖4為系統(tǒng)狀態(tài)變量vx－vy－γ相空間內的相軌跡，圖5為圖4在vy－ω平面的投影。通過相軌跡曲線可以看出，在整個仿真周期內，縱向速度vx由初始值開始經(jīng)歷4次大幅度變化后逐漸減小；側向速度vy和橫擺角速度ω的絕對值由初始值開始經(jīng)歷4次劇烈變化后，在小范圍內波動。各狀態(tài)變量出現(xiàn)顯著的不規(guī)則變化，即車輛系統(tǒng)出現(xiàn)失穩(wěn)運動，并在失穩(wěn)后逐漸趨于靜止。

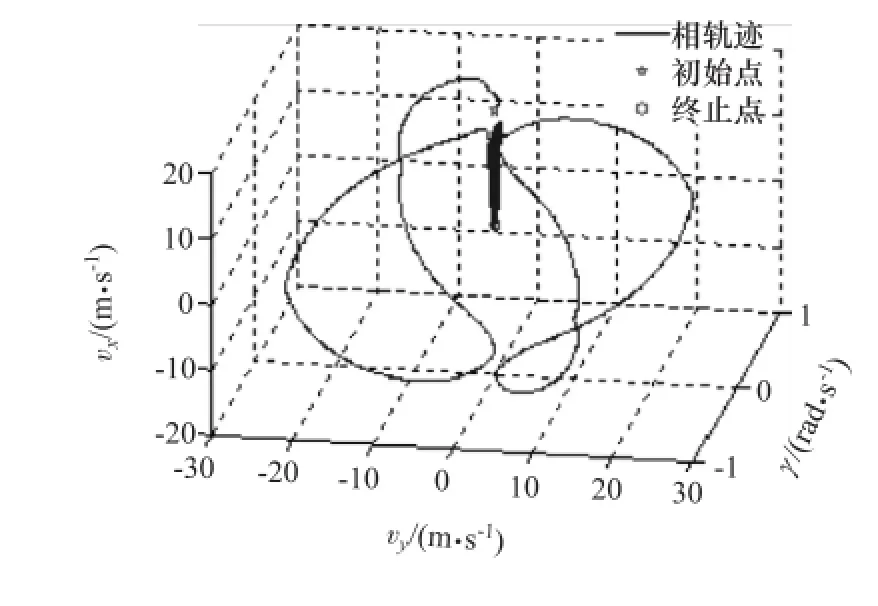
圖4 vx－vy－γ系統(tǒng)相空間特性

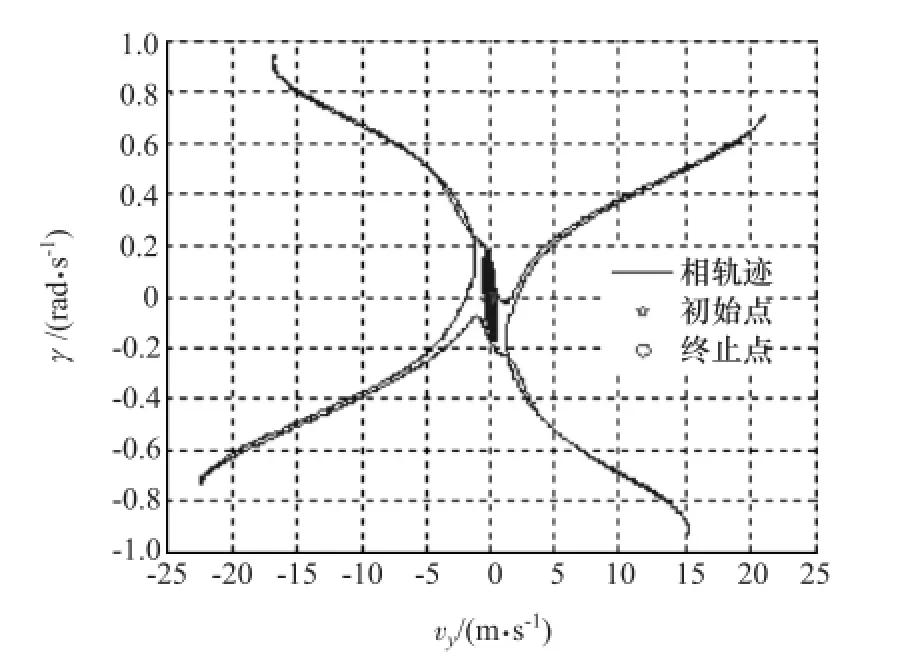
圖5 系統(tǒng)相空間軌跡在vy－γ平面的投影

圖6 為作用在驅動輪上的制動力矩與轉速的數(shù)值計算結果。由圖可見，在仿真終止時驅動輪上的轉速與制動力矩都沒有達到零點。圖7為車輛系統(tǒng)的狀態(tài)變量時間序列圖。由圖可見，仿真200s的時間內，系統(tǒng)橫擺角速度始終在小范圍內波動，縱向速度沒有達到零點。

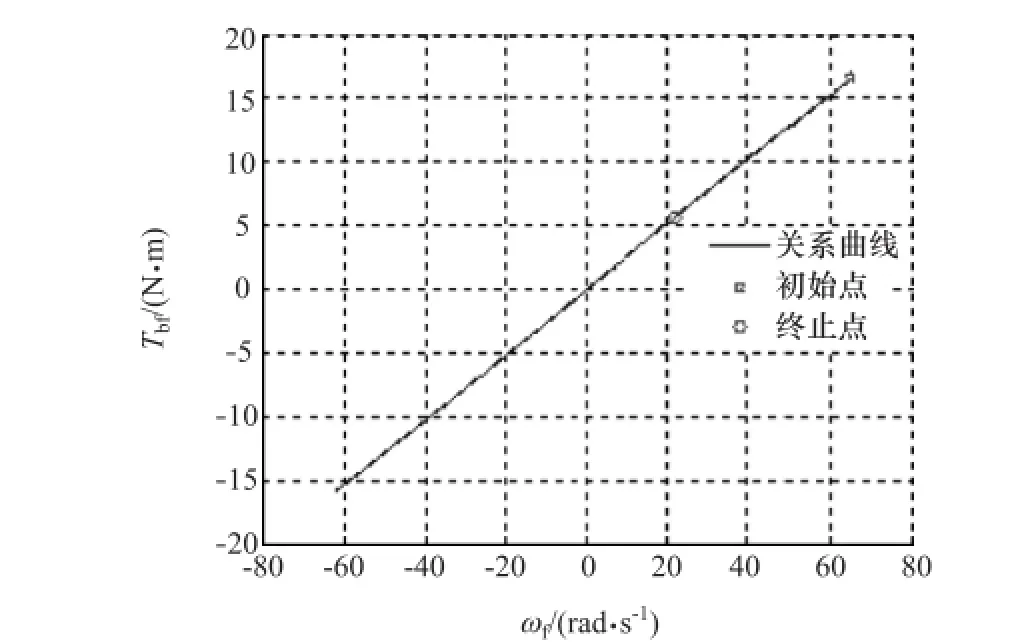
圖6 Tbf－ωf關系曲線圖

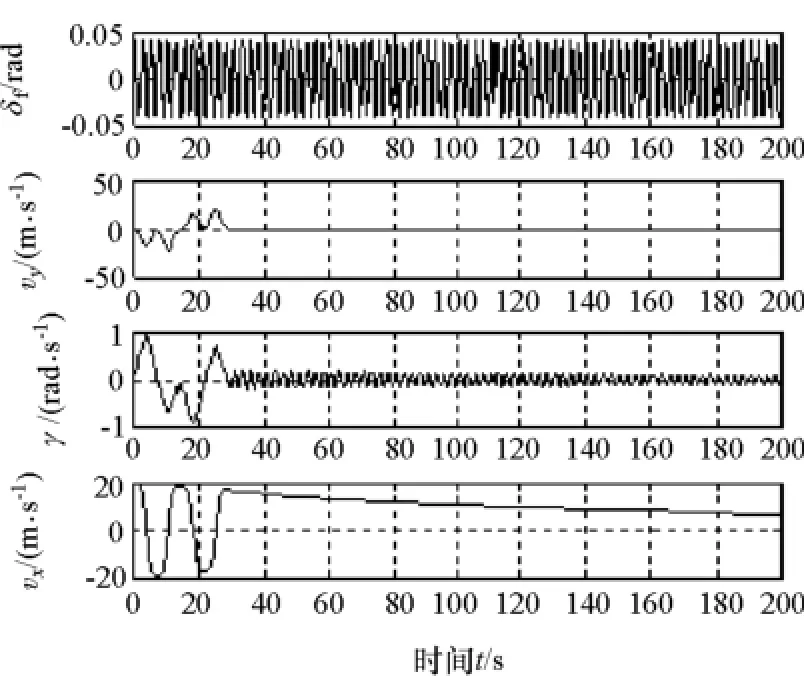
圖7 系統(tǒng)前輪轉角和狀態(tài)變量時間序列

結合實際駕駛經(jīng)驗，高速行駛車輛在轉彎過程中，若只利用發(fā)動機制動實現(xiàn)汽車減速轉向，由于車輛系統(tǒng)為一個耗散系統(tǒng)，經(jīng)過一段時間后系統(tǒng)能量最終耗盡，汽車停止運動，即系統(tǒng)狀態(tài)變量均為零。前期的模型車試驗也表明，在該工況下高速轉向運動的車輛系統(tǒng)能夠在短時間內停止運動。因此，上述仿真結果不符合實際駕駛經(jīng)驗。

2.2 考慮滾動阻力的車輛系統(tǒng)仿真

在與上述仿真初始條件相同的情況下，將滾動阻力加入車輛模型，采用與上述相同的方法進行仿真分析，仿真時間設定為100s。

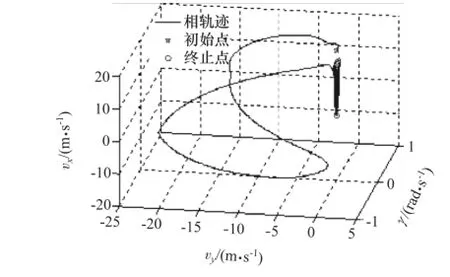
圖8 vx－vy－γ系統(tǒng)相空間特性

圖8 為系統(tǒng)狀態(tài)變量vx－vy－γ相空間內的相軌跡，圖9為圖8在vy－γ平面的投影。整個仿真周期顯示，各個狀態(tài)變量在經(jīng)歷兩次大幅度變化后逐漸減小到零點。圖10為作用在驅動輪上的制動力矩與轉速的數(shù)值計算結果，仿真終止時制動力矩和轉速都到達零點。圖11為系統(tǒng)狀態(tài)變量時間序列圖。由圖可見，仿真時間在接近100s時系統(tǒng)各個狀態(tài)變量達到零點，系統(tǒng)停止運動。這一結果表明，在發(fā)動機制動工況下，車輛系統(tǒng)最終停止運動，與上述不考慮滾動阻力的仿真結果相比，更符合實際情況。由此證明，不考慮滾動阻力的車輛系統(tǒng)模型是不完善的。

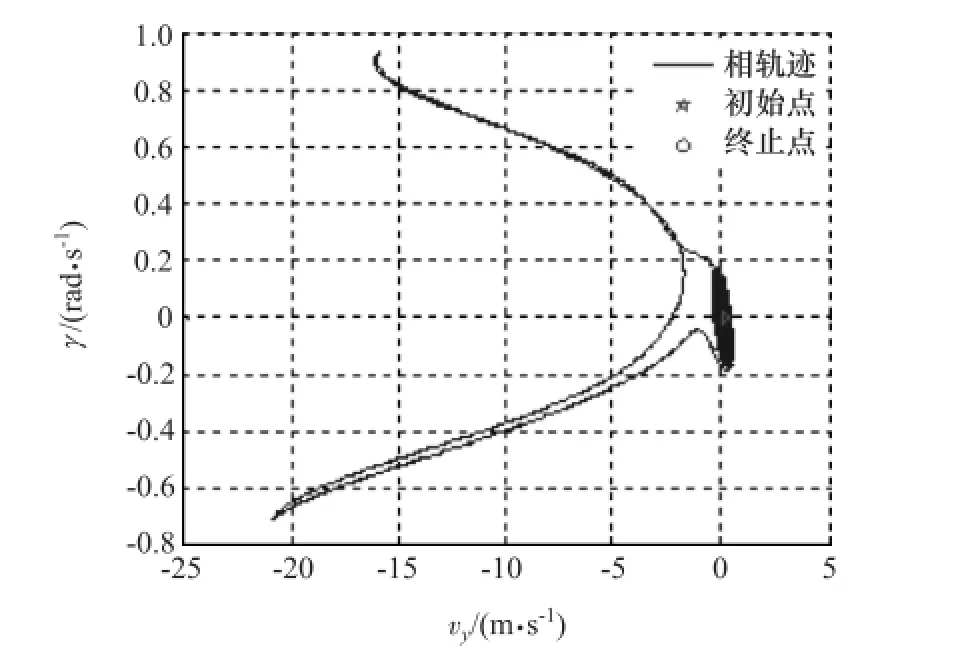
圖9 系統(tǒng)相空間軌跡在vy－γ平面的投影

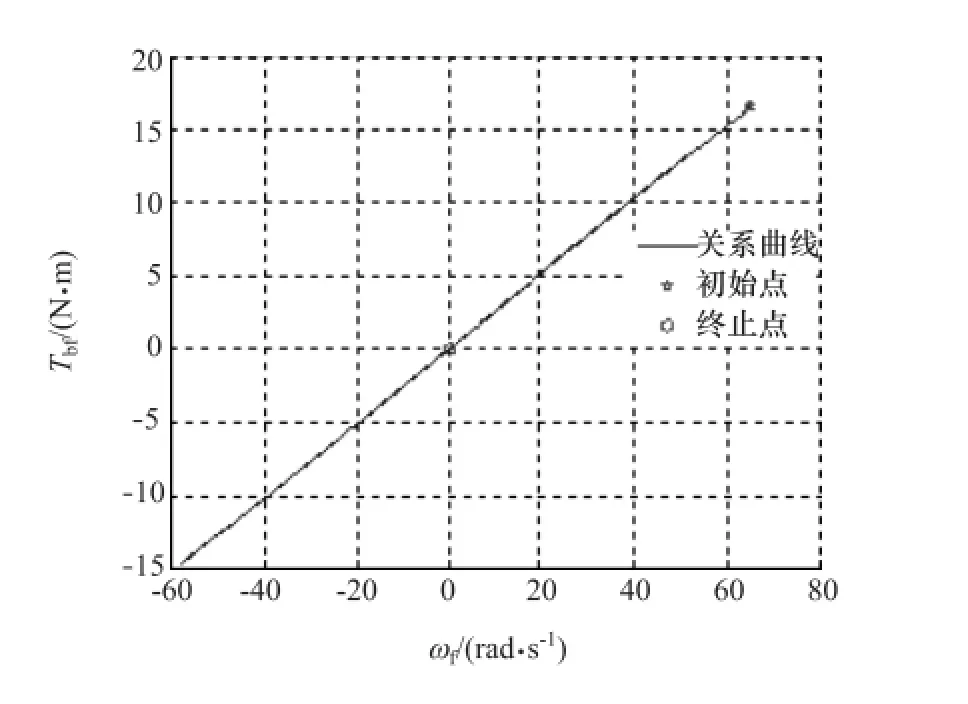
圖10 Tbf－ωf關系曲線圖

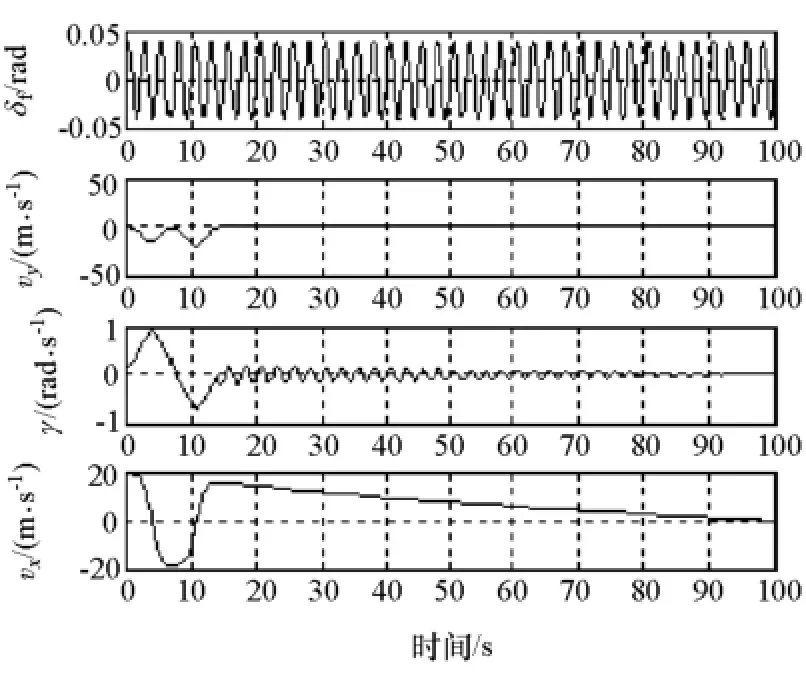
圖11 系統(tǒng)前輪轉角和狀態(tài)變量時間序列

2.3 滾動阻力對車輛系統(tǒng)運動特征的影響分析

將2.1節(jié)和2.2節(jié)中車輛系統(tǒng)3個狀態(tài)變量的前100s仿真數(shù)據(jù)進行對比分析。如圖12～圖15所示，分別為不考慮滾阻和考慮滾阻時，車輛系統(tǒng)縱向速度時間序列圖、側向速度時間序列圖、圖13的局部放大圖和橫擺角速度時間序列圖。

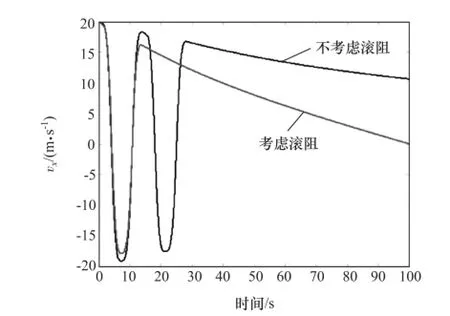
圖12 縱向速度時間序列圖

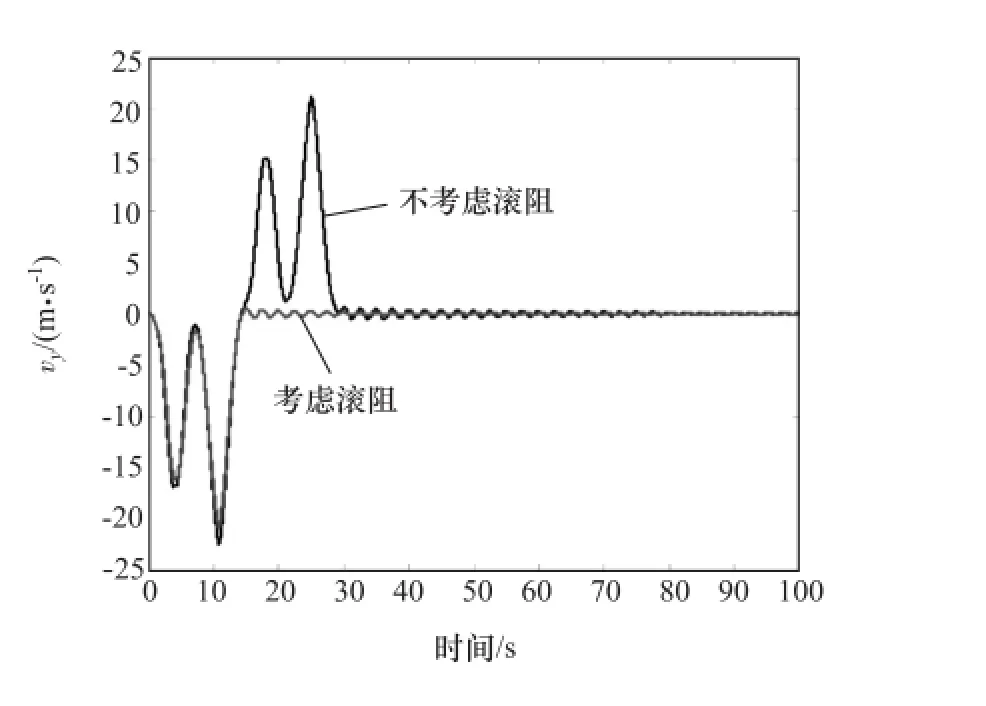
圖13 側向速度時間序列圖

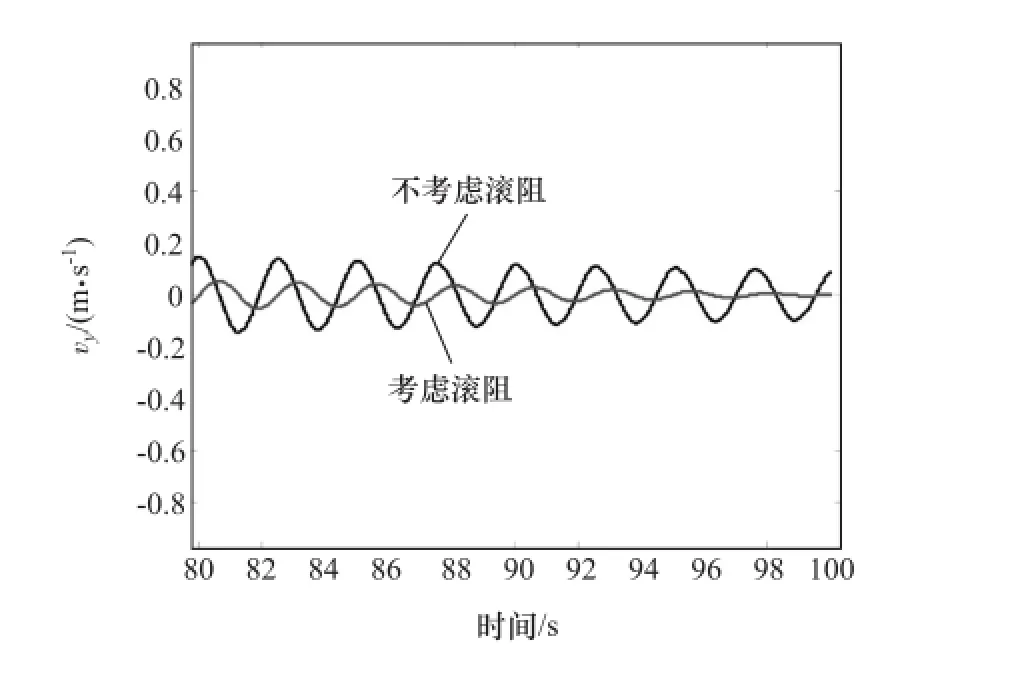
圖14 圖13的局部放大圖

(1)在0－15s的仿真時間內，滾動阻力對車輛系統(tǒng)的縱向速度、側向速度和橫擺角速度的影響不明顯，在該時間段內車輛3個狀態(tài)變量大幅度變化，系統(tǒng)出現(xiàn)失穩(wěn)運動現(xiàn)象。與不考慮滾動阻力的車輛模型仿真結果類似。

(2)在15－35s的仿真時間內，與不考慮滾動阻力的車輛模型仿真結果相比，滾動阻力對車輛系統(tǒng)的運動特征影響非常顯著:不考慮滾動阻力的車輛系統(tǒng)的3個狀態(tài)變量仍大幅度變化，而考慮滾動阻力的系統(tǒng)縱向速度從vx＝15m/s附近逐漸減小，側向速度開始在零附近波動，橫擺角速度在±0.2rad/s的范圍內波動。

(3)在仿真時間接近100s時，不考慮滾動阻力的車輛系統(tǒng)的縱向速度降至11m/s附近，側向速度在±0.15m/s范圍內波動，橫擺角速度在零附近波動；考慮滾動阻力的車輛系統(tǒng)的3個狀態(tài)變量值都為零，系統(tǒng)停止運動。

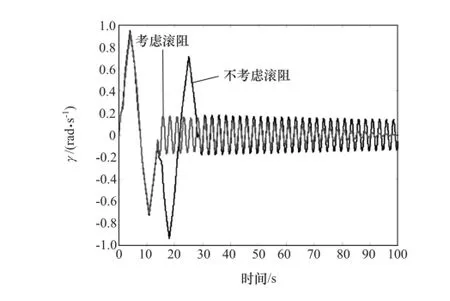
圖15 橫擺角速度時間序列圖

3 結論

本文中研究結果表明，在建立針對發(fā)動機制動工況的車輛系統(tǒng)模型，分析發(fā)動機制動工況下車輛系統(tǒng)的動力學特征時，滾動阻力是一個重要因素。考慮滾動阻力的車輛模型仿真結果顯示，與不考慮滾動阻力的情況相比，滾動阻力不會改變高速時車輛系統(tǒng)的失穩(wěn)運動特征。但在發(fā)動機制動作用下車速逐漸降低的過程中，考慮滾動阻力的車輛系統(tǒng)運動狀態(tài)變化顯著。同時，滾動阻力嚴重影響車輛系統(tǒng)的停止運動時間。建立包含滾動阻力的車輛模型更符合實際，可以為研究發(fā)動機制動工況下車輛系統(tǒng)的操縱穩(wěn)定性提供理論基礎，也為后續(xù)的試驗驗證工作提供了更加準確的仿真模型。

[1] BEYER K，KRUEGER E，SONNENBERG M.Enhanced vehicle stability with engine drag control[C].SAE Paper 2002－01－1217.

[2] WANG Xianbin，SHI Shuming，LIU Li，et al.Analysis of driving mode effect on vehicle stability[J].International Journal of Automotive Technology，2013，14(3):363－373.

[3] INAGAKI S，KSHIRO I，YAMAMOTO M.Analysis of vehicle stability in critical cornering using phase plane method[C].SAE Paper 943841.

[4] YOUNG Eun Ko，LEE Jang Moo.Estimation of the stability region of a vehicle in plane motion using a topological approach[J].Int.J. of Vehicle Design，2002，30(3):181－192.

[5] SOBHAN Sadri，WU Christine.Stability analysis of a nonlinear vehicle model in plane motion using the concept of Lyapunov exponents[J].Vehicle System Dynamics，2013，51(6):906－924.

[6] DELLA Rossa F，MASTINU G，PICCARDI C.Bifurcation analysis of an automobile model negotiating a curve[J].Vehicle System Dynamics，2012，50(10):1539－1562.

[7] SHINICHIRO Horiuchi.Evaluation of chassis control method through optimisation-based controllability region computation[J].Vehicle System Dynamics，2012，50，Supplement:19－31.

[8] ALAN N Gent，JOSEPH D Walter.The pneumatic tire[M].U.S. Department of Transportation:The National Highway Traffic Safety Administration，2006.

[9] RAJAMANI R.Vehicle dynamics and control[M].Springer Science＆Business Media，2011.

[10] GILLESPIE T D，趙六奇，金達鋒.車輛動力學基礎[M].北京:清華大學出版社，2006.

[11] 余志生.汽車理論[M].北京:機械工業(yè)出版社，2009.

[12] 米奇克，瓦倫托維茨.汽車動力學[M].陳蔭三，余強，譯.北京:清華大學出版社，2009.

[13] 莊繼德.汽車輪胎學[M].北京:北京理工大學出版社，1996.

[14] PACEJKA H.Tire and vehicle dynamics[M].Elsevier，2005.

[15] PACEJKA H B，BAKKER E.The magic formula tyre model[J]. Vehicle system dynamics，1992，21(S1):1－18.

[16] WOLF-HEINRICH H，AHMED S R.Aerodynamics of road vehicles:from fluid mechanics to vehicle engineering[M].Elsevier，2013.

[17] 李玲，施樹明，王玉瓊.發(fā)動機制動影響高速轉向車輛穩(wěn)定性的仿真分析[C].2015中國汽車工程學會年會論文集(Volume3)，2015.

[18] GENTA G，MORELLO L.Steering system[J].The Automotive Chassis:Vol.1:Components Design，2009:239－268.

[19] JAZAR R N.Vehicle dynamics:theory and application[M].Springer Science＆Business Media，2013.

[20] PACEJKA H B.Tyre and vehicle dynamic[M].Oxford:Elsevier，2006.

Analyses on the Effects of Rolling Resistance on the Motion Stability of Vehicle

Li Ling1，Shi Shuming1，Wang Xianbin2＆Zhang Xiangdong1
1.Traffic College，Jilin University，Changchun 130022； 2.Traffic College，Northeast Forestry University，Harbin 150040

In view of that traditional multi-DOF nonlinear vehicle model based on classic 2 DOF linear vehicle model usually neglects the effects of wheel rolling resistance，leading to inadequacy in reflecting real states of vehicle motion，a 5 DOF(longitudinal velocity，lateral velocity，yaw rate and the rotational velocities of front and rear wheels)nonlinear dynamics vehicle model under engine braking condition with consideration of wheel rolling resistance is established in this paper.The effects of rolling resistance on the dynamics features of vehicle in highspeed cornering are studied by using analysis methods of globe phase plane and state variables time sequence for nonlinear system.Simulation results show that in the course of gradual reduce in vehicle speed under engine braking condition，rolling resistance has significant impact on vehicle motion states.Therefore，vehicle model containing rolling resistance is conducive to the analysis on the handling and stability characteristics of vehicle，providing theoretical supports for the test verification on the correctness of theoretical model.

handling stability；tire rolling resistance；vehicle dynamics；unstable motion

10.19562/j.chinasae.qcgc.2017.04.012

?國家自然科學基金(51475199)、中央高校基本科研業(yè)務費專項資金項目(2572015CB15)和黑龍江省自然科學基金(E2015052)資助。

原稿收到日期為2016年3月28日，修改稿收到日期為2016年5月27日。

施樹明，教授，E-mail:shishuming＠jlu.edu.cn。