基于粒子群優化的自適應模糊制冷控制算法

崔辰鵬，劉雪峰，陳子印，郝中洋

(北京空間機電研究所，北京 100094)

基于粒子群優化的自適應模糊制冷控制算法

崔辰鵬，劉雪峰，陳子印，郝中洋

(北京空間機電研究所，北京 100094)

為解決空間斯特林制冷機和探測器熱負載不確定及存在變化的問題，提出了自適應模糊PID制冷控制;在空間環境中使用的斯特林制冷機參數會隨著時間的變化而發生改變，探測器負載也會隨著工作模式和工作時間的變化而變化，整個制冷系統涉及的變量多，參數非線性;采用傳統的控制方法，在固定的單一條件、環境下得到的控制參數，環境和負載發生變化后容易性能變差甚至不穩定，控制精度和穩定性不能滿足使用要求;設計了一種自適應斯特林制冷機控制器，通過綜合自適應模糊PID控制的方法，采用粒子群優化算法調整控制參數以減小代價函數;通過仿真和試驗驗證算法的有效性和魯棒性。

斯特林制冷機; 自適應; 模糊控制;PID控制; 粒子群優化

0 引言

本文涉及到的空間用斯特林制冷機模型的建立比較困難，在實際中，被控對象的數學模型是隨著時間和工作環境的變化而變化[1-2]。因被控對象的工況在大范圍變化的情況下，常規PID調節器需要經常進行參數調整，否則就無法達到良好的控制效果。

大量事實證明，將粒子群算法、模糊控制技術和經典控制技術相結合構成的復合控制技術在求解優化問題方面有著無比的優越性，可以達到更加理想的控制精度和控制效果[3]。采用這種復合控制技術的使用前景，具有重大的理論與現實意義。

文[4]提出了一種基于Smith預估器的模糊PID控制，文[5]對斯特林制冷機的熱力動態模型進行了詳細深入的研究，文[6]對斯特林制冷機直線壓縮機的傳遞函數進行了建模。自適應PID控制方法在控制領域有很多應用，文[7]和文[8]分別是自適應PID控制在永磁同步電機和溫度控制系統中的應用，參考借鑒以往的科研成果，文獻[9]提出的一種高精度的制冷型紅外探測器的溫度控制系統，設計了一種基于自適應模糊PID復合控制策略[10]，控制參數如比例、積分因子隨著輸入輸出的控制參數變化而自動調整[11]。這種方法應用到制冷機控制中實現控制參數的自整定，提高控制系統對環境和負載特性變化的適應能力。

由于系統的穩定性和動態性能均決定于控制器參數的選擇，所以采用粒子群優化算法對控制參數進行調節[12]。粒子群優化算法是現代啟發式搜索算法基于群智能，能夠適用于不同領域的優化問題[13]，具有結構簡單，算法計算代價低，性能良好的優點。可以提高系統的穩定性和動態性能。

文[14]和文[10]分別對斯特林制冷機的關鍵參數和熱傳導特性進行了詳細的闡述，這種控制系統和其他制冷系統[15-19]相比具有單向只能制冷不能制熱的特點，極易受到環境溫度和負載的影響，控制系統的特性是動態變化的。高性能的制冷機控制系統[20]要求控溫精度和控溫穩定性要好，對穩定時間短，能夠適應不同的控制模式實現不同溫度點的閉環控制，穩態無靜差，對系統特性和環境變化具有強魯棒性，比文[21] 采用的制冷方法制冷量大、制冷溫度低。

空間條件下，真空環境和熱環境復雜，產品特性存在變化的系統，適應不同負載和環境的能力是衡量制冷機控制系統的重要指標之一。

基于以上思想，本文的創新點總結如下：

1)本文針對斯特林制冷機采用自適應控制算法；

2)利用粒子群優化算法調整控制器參數，提高系統的穩定性和動態性能。

本文結構如下：第二節介紹制冷機模型。第三節進行控制器設計。第四節利用粒子群算法優化控制器參數。仿真結果在第五節給出。

1 基于自適應模糊PID控制的低溫制冷機控制系統

1.1 斯特林用直線壓縮機數學模型

直線壓縮機的單自由度模型可以用以下微分方程[6]來描述：

活塞運動方程：

(1)

電磁系統方程：

(2)

式中,mc為運動振子質量，x為活塞位移，f為等效阻尼系數，Ac為活塞截面積，Pc為氣缸內氣體壓力，K為機械彈簧剛度，H為磁感應強度，l為線圈長度，I為線圈電流，PAV為活塞背壓，L為線圈自感系數，R為線圈電阻，U為輸入電動勢，Uind為感應電動勢。

將氣體力與彈簧力合在一起得到一個綜合彈簧系數 ，振子質量產生的重力與其它作用力相比很小可以忽略，活塞運動方程可表示為：

(3)

1.2 直線壓縮機傳遞函數

制冷機直線壓縮機的輸入電壓和活塞之間的關系可以用傳遞函數的形式表示出來。

對式(2)和式(3)等式兩邊進行拉氏變換可得：

LsI(s)+RI(s)=U(s)-HlsX(s)

(4)

mcs2X(s)+fsX(s)+KzX(s)=HlI(s)

(5)

求解以上方程組可得傳遞函數：

(6)

根據式(4)和式(5)的輸入、輸出關系建立如圖1的傳遞函數方框圖。

圖1 直線壓縮機傳遞函數方框圖

由以上建立起輸出驅動電壓和活塞運動距離之間的關系，根據文獻[5]、[22]，使用特定制冷機機械參數、充氣壓力等參數和制冷機焦面溫度之間的測試數據，得到活塞運動位移和焦面溫度之間的關系，以經驗公式的形式存儲。加入圖1中，形成溫度閉環。

2 自適應模糊PID控制系統

空間斯特林制冷機控制應用中采樣周期不定，而且控制算法的計算周期是變化的,同樣的算法在反饋參數不同時計算時間可能不同。探測器和制冷機在空間環境下存在性能退化的現象,熱負載和環境存在變化,制冷系統遲滯時間長,傳統的控制方法難以實現穩定控制。設計一種自適應模糊整定系統,對傳統PID算法進行改進,對反饋的溫度信號和目標溫度求差,按照設定的模糊規則,以溫度差值以及差值變化量為輸入,實現比例、積分、微分參數的自適應調整[21-23]。

設定當前溫度信號和目標溫度差值為e,差值變化為ec,按照一定控制律對比例Kp、積分Ki、微分Kd參數實時自適應調整,模糊PID控制器結構框圖如圖2。

圖2 模糊PID控制器結構框圖

控制系統以溫度差值以及差值變化量為輸入, 比例Kp、積分Ki、微分Kd的調整規則即模糊矩陣如表1～3所示。

表1 Kp整定原則

表2 Ki整定原則

表3 Kd整定原則

設“NB,NM,NS,Z,PS,PM,PB”為”-3,-2,-1,0,1,2,3”,根據e和ec,按照模糊規則按照式(7)對比例Kp、積分Ki、微分Kd參數進行調整。

kp=kp0+Δkp,ki=ki0+Δki,kd=kd0+Δkd

(7)

PID參數自適應調整工作流程如圖3所示。

圖3 模糊PID工作流程圖

3 基于粒子群的模糊PID參數優化結構

粒子群優化算法，是美國電氣工程師Eberhart和社會心理學家Kennedy在1995年提出的，是一種提出時間較晚相對較新的優化算法。粒子群優化算法中的每個粒子都是優化問題的一個解，粒子通過迭代找到最優解實現對參數 優化[24]。粒子群算法的原理簡單容易理解，優化設置的初始參數較少，整體收斂速度較快，是一種實現方便的優化算法，已經逐步成為智能優化領域的研究熱點。

3.1 粒子群優化

粒子群在優化算法中處于遺傳算法和進化規劃之間，是一個非常簡單的能夠有效優化各種函數的算法。粒子群算法運用的是速度和位移的方法，算法本身思想直觀，相對于遺傳算法和進化規劃來說比較簡單容易實現。

系統的控制性能不僅受到模糊規則的影響，還與控制器量化因子和比例因子的大小有關。

本文設計的基于粒子群的模糊PID控制器基于這種思想，通過粒子群算法對模糊PID控制器的量化因子Ke、Kec和比例因子K1、K2、K3進行參數優化[25]。基于粒子群優化算法的模糊PID參數優化結構框如圖4所示。

圖4 基于粒子群的模糊PID優化結構圖

基于粒子群的模糊PID參數優化步驟如圖5所示。

圖5 粒子群優化模糊PID流程圖

粒子群優化模糊PID參數的具體實現過程：

1)粒子群優化算法初始化。待優化的參數分別是量化因子Ke、Kec和比例因子K1、K2、K3，所有本粒子群優化維數為5；設定本文的慣性權重ω在[0.9, 0.4]之間線性下降；速度限幅vmax為粒子范圍的0.1～0.2倍；為了便于優化，本文采用30個粒子，50次迭代，初始的搜索空間設置在已知數據的上下空間內。

2)適應值計算。在本文的粒子群算法中，適應值指的是每個粒子的控制性能指標，通過指標來優化量化因子和比例因子。對于PID控制器，典型的控制系統的動態性能指標包括上升時間、峰值時間、超調量、調節時間和穩態誤差等。這些指標只能體現某一性能方面，而不能綜合體現控制器的性能。綜合性指標包括ISE、IAE、ITAE、ISTE等。本文對斯特林制冷機的自適應PID控制器的參數優化，采用的指標為ITAE指標[26]，即時間與絕對誤差乘積積分指標，它能夠綜合體現系統的偏差和時間之間的關系，其值越小越好，表達式可描述為:

(8)

3)粒子群的更新和停止。有圖5可以看出，整個優化過程主要分為兩個部分，一個是粒子群算法的步驟，另一個是Simulink模型，兩者之間相互合作。粒子群算法產生粒子并交給Simulink模型產生適應值結果，然后將適應值結果傳給粒子群算法進行計算。當粒子群算法滿足終止條件，即達到最大迭代次數或者達到設定的性能指標時，算法終止。將計算得到的量化因子和比例因子作為模糊自適應PID控制器的參數輸入到仿真模型當中，輸出仿真圖形。

本節采用粒子群優化算法對控制器參數進行調節，減少迭代次數和時間，采用控制系統常用時間絕對誤差積分的評價形式:

(9)

其中:T仿真時間，系統誤差e，誤差變化率ec。

粒子群的粒子的位置和速度的更新方程如下:

(10)

(11)

其中:c1和c2為認知因子，w慣性權重，r1和r2隨機函數 (0,1]，x和vi分別表示粒子的位置和函數，pbesti表示當前最優值xi，gbest全局最優值。

控制慣性權重的大小，可以改變公式(10)中的第一項，改變上一個速度的影響。一個慣性權重w隨著時間遞減的方法將會使粒子群得到更好的尋優效果，慣性權重w線性遞減公式為：

(12)

式中，wmax表示算法開始應用的最大數值，wmin表示算法最后應用的最小數值，Tmax表示設置的最大迭代次數，t表示當前的迭代次數。

4 系統仿真及結果

4.1 制冷機溫度控制系統框圖

基于上述控制策略，并結合制冷機實際參數，建立圖6的制冷機溫度控制模型[4]，在此系統上進行對常規PID控制、自適應模糊PID控制方式進行比較。

由文獻[27]通過擬合的方式得到直線壓縮機和溫度之間的近似關系，用函數F(x)標示，F(x)表示在活塞最大行程為X的輸入正弦驅動電壓穩定工作時，探測器內部能夠穩定到的溫度，單位為K。實際工程中通過測量封裝在探測器中的測溫二級管兩端的電壓，得到反饋溫度，單位為V，每一個電壓Vi值對應探測器內部的穩定Ti。

圖6 制冷機控制器結構框圖

其中:T’為目標溫度，T為探測器溫度。

4.2 基于粒子群的模糊PID參數優化仿真

仿真模型采用Simulink中的模塊搭建結構如圖5所示，粒子群優化的流程圖如圖7所示

圖7 粒子群算法的流程圖

仿真過程包括Simulink仿真模型、粒子群優化算法程序、粒子群算法與Simulink模型的連接程序三個部分。

第一部分：在制冷機自適應模糊PID控制器基礎上建立粒子群尋優的系統仿真模型。在模型中加入ITAE指標部分，通過將時間與誤差絕對值的乘積進行積分后得到，并設置輸出端口1的輸出值將作為粒子群算法的適應值。如圖8所示。

圖8 基于粒子群的模糊自適應PID控制系統

模糊自適應PID控制系統的子模塊如圖9。

圖9 模糊控制系統的子模塊

第二部分：在圖5中，采用m文件編寫連接程序表示粒子群優化算法和Simulink仿真模型的連接模塊。在m文件將x(1)、x(2)、x(3)、x(4)、x(5)的值賦值給Workspace中的K1、K2、K3、Ke、Kec，將參數送入模型之中進行仿真，將得到的性能指標結果傳遞給粒子群部分。

第三部分：編寫粒子群算法程序，在程序當中調用第二部分的仿真程序，將第二部分得到的適應值結果直接應用到粒子群算法當中。

4.3 仿真結果比較分析

4.3.1 自適應模糊控制和PID控制結果比較

采用自適應模糊控制如圖9所示，參數為K1=1/3，K2=1/3，K3=1/3，Ke=0.5，Kec=30。由圖10比較可知，自適應模糊PID控制的穩定性和抗干擾能力優于常規PID控制。響應階躍溫度控制命令過程中，自適應模糊PID控制和只采用PID控制算法時引起的溫度超調小，能快速穩定；溫度穩定控制時，外界環境溫度和熱負載發送變化時，自適應模糊PID控制能使控制溫度快速達到穩定，波動性小，抗干擾能力強，而只采用PID控制算法的控制器受外界影響較大并且容易失穩。由此，自適應模糊PID控制響應快、穩定時間短，而且對負載變化有更好的適應能力，控制系統有很好的跟隨性、穩定性和魯棒性。

圖10 自適應模糊PID控制和PID控制系統階躍響應結果

4.3.2 粒子群優化前后自適應模糊控制結果比較

參數估計的初始值如上小節所示。采用粒子群算法尋優后得出的最優參數分別是K1=-9.1184，K2=0.3719，K3=10，Ke=-2.1612，Kec=22.3812，最優性能指標為J=645，粒子群優化過程中的適應值變化曲線如圖11所示。

仿真結果如圖所示，圖11給出了代價函數隨優化迭代次數的變化曲線，圖12給出了優化迭代過程中的最優控制參數對應的系統響應曲線，表明了優化算法的有效性，優化后的控制器具有較快的瞬態響應速度，較小的穩態誤差。

圖11 代價函數隨優化迭代次數變化曲線

將用粒子群尋優后的模糊自適應PID控制器的仿真結果與參數未優化時的仿真結果放在同一個圖中進行比較，仿真輸出結果如圖12所示。

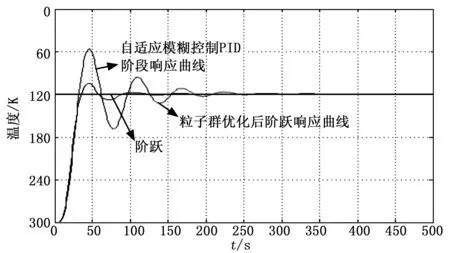
圖12 粒子群優化前后模糊自適應PID控制器輸出曲線

由圖12中可以看到，紅色曲線表示粒子群算法優化前的自適應模糊控制制冷機溫度的輸出曲線，藍色曲線代表用粒子群算法優化后制冷機溫度的輸出曲線，綠色代表階躍信號。兩種控制方案溫度最后都穩定在正常范圍內的120 K，但從曲線中可以明顯看出，經粒子群算法優化后的制冷機溫度輸出曲線具有超調量小、上升時間短、調節時間短、穩定誤差小的特點，控制系統具有更加優秀的控制性能。

5 結論

本文針對斯特林制冷機的模型進行了分析，提出了一種自適應模糊PID復合控制策略，并將其應用到斯特林制冷機的溫度閉環控制中去。在自適應模糊PID控制器的基礎上，采用標準粒子群算法對其量化因子進行優化。結果表明，經過粒子群算法優化之后，控制性能得到明顯提高。通過分析不同控制算法下系統性能，得出以下結論：

1)傳統方法在系統參數變化或負載擾動情況下，控制效果不理想；

2)應用自適應模糊控制思想，設計了一種在線自整定的PID參數調整機構，無需對控制對象進行精確辨識和建模，將其應用到斯特林制冷機閉環溫度控制中。實驗結果驗證了該策略的有效性。

3)采用粒子群優化算法對控制參數進行優化調節，保證系統的穩定性和動態性能，最后通過仿真和實驗驗證了控制優化算法的有效性。與傳統方法相比，本文方法具有溫度調整速度快、穩定性高、抗干擾能力強的特點。

[1] 閆春杰, 潘雁頻, 許國太, 等, 斯特林制冷機與紅外探測器耦合集成技術[J]. 航天返回與遙感, 2011, 32(2): 64-67.

[2] 金占雷, 孫啟揚, 張新玉, 等, 基于辨識的低溫制冷系統控制率設計方法[J]. 航天返回與遙感, 2016, 37(1):48-54.

[3] 劉 軍, 朱 杰. 復雜熱工過程智能控制與應用[M]. 北京: 兵器工業出版社, 2005.

[4] 楊 珂. 基于Smith預估器的模糊PID控制在中央空調系統中的應用[D]. 衡陽：南華大學, 2010.

[5] 吳卓林. 分置式斯特林制冷機的熱力動態模型及仿真的研究 [D]. 合肥: 合肥工業大學, 2004.

[6] 劉向農, 唐景春, 吳 昊, 等, 斯特林用直線壓縮機的傳遞函數法建模[A]. 低溫與超導, 第九屆全國低溫工程大會論文集[C]. 2009:269-272.

[7] 崔家瑞, 李 擎, 張 波, 等, 永磁同步電機變論域自適應模糊PID控制[J]. 中國電機工程學報, 2013, 33: 190-194.

[8] 歐陽磊, 基于自整定PID控制器的溫度控制系統研究[D]. 淮南: 安徽理工大學, 2010.

[9] 黃新棟. 制冷型紅外探測器高精度制冷控溫系統[J]. 紅外技術, 2012, 34( 9): 547-550.

[10] 徐瑞萍, 徐烈, 趙蘭萍. 粗糙表面接觸熱阻的分形描述[J].上海交通大學學報,2004, 38(10):1609-1612.

[11] 吳艷敏, 關英姿, 王福生, 等, 基于模糊自適應PID的轉臺位置控制系統設計[J]. 現代電子技術, 2008, 19:102-104.

[12] Mohd A M B, Abdul R H, Kumeresan A D.Enhanced backstepping controller design with application to autonomous quadrotor unmanned aerial vehicle[J]. Journal Intelligent Robot System, 2015,79(2):295-321.

[13] Eberhart R C, Shi Y, Kennedy J. Swarm Intelligence[D]. Morgan Kaufmann, Burlington,MA, 2001.

[14] 蔡 詩, 李 娜, 陳 曦, 等. 氣動斯特林制冷機關鍵參數的模擬與實驗[J]. 低溫工程, 2014, 200(4): 51-54.

[15] Jin Y B, Shao X N, Zhuang M, et al. EAST Cryogenic supervisory and control system based on Delta-V DCS[J].Plasma Science & Technology, 2005,7(5): 3013-3016.

[16] Gomes P, Balle C, Blanco E,Casas J,et al, Experience with the String2 Cryogenic Instrumentation and Control System[A]. Accelerator Technology Department[C]. CERN, 1211 Geneva 23, Switzerland.

[17] Jin Y B, Zhuang M, Bai H Y. Preliminary design of control network for HT-7U Tokamak cryogenic system[A]. Plasma Science & Technology[C]. 2003, 5(6):2035-2038.

[18] Li G, Wang K X, Zhao J J, et al, The cryogenic control system of BEPC II[J]. Chinese Physics C (HEP & NP) , 2008, 32(4):294-296.

[19] Axensalva J, Herblin L, Lamboy J P, et al, Control system and operation of the Cryogenic Test Facilities for LHC Series Superconducting Megnets[J]. CERN-AT Department, CH-1211, Geneva 23, Switzerland.

[20] 楊寶玉, 吳亦農, 府 華, 等, 斯特林制冷機自適應主動振動控制技術[A]. 低溫工程會議[C]. 2009:50-53.

[21] 張明濤, 謝仁飚, 朱 磊, 等, 320x256短波紅外焦平面溫控系統設計與應用[J] .紅外與毫米波學報, 2009, 28(3):173-176.

[22] 陳長琦, 吳卓林. 分置式斯特林制冷機的物理模型及動態特性分析[J]. 流體機械, 2003, 31(12): 47-50.

[23] 劉金琨, 先進PID控制MATLAB仿真(第3版)[M]. 北京: 電子工業出版社, 2011.

[24] 張庭場, 耿光飛. 基于改進粒子群算法的中壓配電網無功優化[J]. 電網技術, 2012, 2: 158-162.

[25] 汪陽華. 基于粒子群算法的鍋爐主蒸汽壓力模糊PID控制[J]. 湖南工業大學學報, 2012, 26(5): 62-66.

[26] 應明峰, 王海洋, 翟立新. 一種云自適應粒子群優化的模糊PID控制器設計[J]. 計算機測量與控制, 2013, 21(12): 3278-3280.

[27] 陳 楠. 大冷量斯特林制冷機用動磁式直線壓縮機關鍵特性及整機性能研究 [D].上海:上海交通大學, 2007.

ParticleSwarmOptimizedAdaptiveFuzzyCryocoolerControlAlgorithm

CuiChenpeng,LiuXuefeng,ChenZiyin,HaoZhongyang

(BeijingInstituteofSpaceMechanics&Electricity,Beijing100094,China)

To solve the control problem of stirling cryocooler for space using and detector load in the present of parameter uncertainties and changes, we design an adaptive fuzzy PID method for cryocooler control. Space using stirling cryocooler parameter is changing with time and different environment, detector load is changing with working mode and working hours, the whole cooling system is a multi-variable, nonlinear control system. Traditional control method is designed in certain condition cannot fulfill the accuracy and stability with different environment and load changing. This paper puts forward an adaptive fuzzy PID controller according to the different cold quantity and types of need of refrigeration of the detector load, control parameters is realized by using fuzzy control of self-adjustment. Particle swarm optimization (PSO) algorithm is adopted to determine the optimal parameters for the controller by minimizing the objective function. Finally, the simulation and test results are presented to proof the effectiveness and robustness of the proposed controller.

stirling cryocooler; adaptive control; fuzzy control; PID control; Particle swarm optimization

2017-01-22；

2017-02-15。

崔辰鵬(1986-), 男, 河南人, 碩士研究生, 工程師, 主要從事遙感器控制技術方向的研究。

1671-4598(2017)04-0075-05DOI：10.16526/j.cnki.11-4762/tp

TP

A