函數的性質 導參的法寶
函數的性質 導參的法寶
■湖北省巴東縣第三高級中學 廖慶偉
函數問題中求參數的值或參數范圍在高考試題中經常出現,也是同學們學習的難點,解這類題時常常用導數的幾何意義、函數的奇偶性、函數的單調性、函數的極值、函數圖像的對稱性、函數的零點導出參數的值或范圍。
一、用導數的幾何意義“導”參數
(2 0 1 6年高考新課標Ⅱ卷理數)若直線y=k x+b是曲線y=l nx+2的切線,也是曲線y=l n(x+1)的切線,則實數b =_____。
設直線y=k x+b與函數y=l nx+2的圖像相切于點P1(x1,y1),與函數y=l n(x+1)的圖像相切于點P2(x2,y2),故
又y1=l nx1+2,y2=l n(x2+1),所以
設直線y=k x+b與函數y=l nx+2的圖像相切于點P1(x1,y1),與函數y=l n(x+1)的圖像相切于點P2(x2,y2)。
故y1=l nx1+2,y2=l n(x2+1)。
因為點P1(x1,y1)在切線y=k x+b上,所以
由P2(x2,y2)在切線上得y-l n(x2+1),這兩條直線表示同一條直線,故:
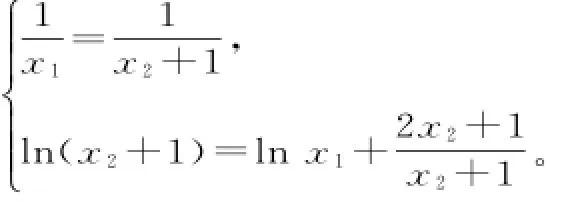
所以b=l nx1+2-1=1-l n2。
點評:解法1是分別求出兩個函數的導數,設出兩個切點的坐標,利用導數得到兩個切點之間的關系,進而求出切線斜率,求出b的值。解法2是分別求出兩個函數的導數,設出兩個切點的坐標,由點P1、P2都在切線上,得出關于x1、x2的方程組,解出x1,求得k的值,從而求出b的值。
二、用函數的奇偶性“導”參數
設a∈R,函數f(x)=ex-ae-x的導函數為f'(x),且f'(x)是奇函數,則a=( )。
A.0 B.1 C.2 D.-1
解法1:因為f(x)=ex-ae-x,所以f'(x)=ex+ae-x。由于f'(x)是奇函數,所以ex+ae-x+e-x+aex=0恒成立,即(a+ 1)(ex+e-x)=0恒成立。
解得a=-1,故選D。
解法2:因為f(x)=ex-ae-x(x∈R),所以f'(x)=ex+ae-x(x∈R)。
由于f'(x)是奇函數,故f'(0)=0,解得e0+ae-0=0。
解得a=-1,故選D。
點評:由于f'(x)是奇函數,可利用f'(x)+f'(-x)=0求參數a的值。若奇函數f(x)的定義域包含0,則f(0)=0。
三、用函數的單調性“導”參數
(河南鄭州一中2 0 1 6屆高三文科考前沖刺)已知函數∈R,在區間[0,1]上單調遞增,則實數a的取值范圍是______。
由f'x()>0解得e2x>a,即x>此時函數單調遞增;
由f'x()<0解得e2x<a,即x<此時函數單調遞減。
綜上,實數a的取值范圍是-1,1[]。
點評:若函數在已知區域單調,求參數的范圍,常常轉化為導數恒成立問題來求解。求函數的導數,利用函數的單調性和導數之間的關系進行求解,注意要對a進行討論,把a分為a>0,a=0,a<0三種情形,當a>0時,注意所求函數的單調區間與所給區間之間的關系,當a<0時,注意函數值的符號。
四、用函數的極值“導”參數
(陜西省黃陵中學2 0 1 6屆高三模擬)若函數f x()=xl nx-a x2有兩個極值點,則實數a的取值范圍是( )。
C.(1,2) D.(2,e)
解析:由題意得f'x()=l nx+1-2a x =0有兩個不相等的實數根,故f″x()=必有解,則a>0,并且0。解得選A。
點評:已知極值求參數,若函數f(x)在點(x0,y0)處取得極值,則f'(x0)=0,且在該點左、右兩側的導數值符號相反。使f'(x) =0的點未必是極值點,但是可導函數的極值點處的導數必為0。
五、用函數的對稱性“導”參數
設f(x)=2x3+a x2+b x+1的導數為f'(x),若函數f'(x)的圖像關于直線x=稱,且f'(1)=0,求實數a、b的值。
解析:依題意得f'(x)=6x2+2a x+b。又函數f'(x)的圖像關于直線x=1對稱, 2所以,解得a=-3。
由f'(1)=0,得b=0。
點評:三次函數的導函數恰為二次函數,利用二次函數a x2+b x+c=0(a≠0)的對稱軸為可求解。
練一練:
(2 0 1 6年高考新課標Ⅰ卷改編)已知函數f(x)=(x-2)ex+a(x-1)2有兩個零點,則實數a的取值范圍是_____。
參考答案:(0,+∞)。
(責任編輯 徐利杰)
- 中學生數理化(高中版.高二數學)的其它文章
- 有機化學專項訓練(二)
- 解讀烴和鹵代烴知識考查熱點
- 烴類易混淆點突破
- 烴類高考常見考點直擊
- 電磁感應綜合應用檢測題
- 電磁感應新穎試題賞析

