導數及其應用問題例析

導數及其應用問題例析

■河北省衡水市鄭口中學 張志勇

導數的應用十分廣泛,如求函數的單調區間、極值、最值,求曲線的切線以及解決某些實際問題等。利用導數可使復雜問題變得簡單,導數為研究函數的單調性以及極值問題等提供了解題思路和方法,因而成為新高考的一個熱點。高考對導數的要求主要表現在三個方面：①考查導數的概念、求導公式和求導法則;②導數的簡單應用,包括求函數的極值,求函數的單調區間,證明函數的增減性等;③綜合考查,常以應用問題或有關導數內容的綜合問題出現。

一、導數的幾何意義

導數的實質是函數值相對于自變量的變化率,體現在幾何意義上就是切線的斜率。利用導數的幾何意義,研究曲線的切線的斜率是導數的一個重要內容。求切線的方程可通過求導數先得到斜率,再由切點利用點斜式方程得到,求過點P(x0,y0)的切線方程時,一要注意P(x0,y0)是否在曲線上,二要注意該點可能是切點,也可能不是切點,因而所求的切線方程可能不止1條。已知曲線C：y=x3-3x2+2x,直線l：y=k x,并且l與C切于點(x0,y0) (x0≠0),求直線l的方程及切點坐標。解析：直線l過原點,知點(x0,y0)在曲線C上

則過點P(1,m)的切線斜率為k=f'(1)= -1-4a。

又切線方程為3x-y+b=0,故-1-4a= 3,即a=-1。

二、運用導數有關知識研究函數的單調性和最值(極值)問題

1.求函數單調區間的步驟為：①確定函數的定義域;②求導函數f'(x);③解不等式f'(x)＞0,得f(x)的遞增區間;解不等式f'(x)＜0,得f(x)的遞減區間,即函數的增區間是f'(x)≥0恒成立的區間,函數的減區間是f'(x)≤0恒成立的區間(導數值為零的點為有限個)。

利用求導方法討論函數的單調性,要注意以下幾方面：①在某個區間上f'(x)＞0是f(x)在該區間上遞增的充分條件而非必要條件(f'(x)＜0亦是如此);②求單調區間時,首先要確定函數的定義域,然后再根據f'(x)＞0或f'(x)＜0,解出在定義域內相應的x的取值范圍。設a∈R,已知函數(a x2+a+1)(e為自然對數的底數)。

令g(x)=-a x2+2a x-a-1。

①當a=0時,g(x)=-1＜0,f'(x)＜0,f(x)在R上為減函數。

②當a＞0時,方程g(x)=0的判別式Δ=4a2-4(a2+a)=-4a＜0,g(x)＜0,即f'(x)＜0,f(x)在R上為減函數。

③當a＜0時,由-a x2+2a x-a-1＞ 0,得

由-a x2+2a x-a-1＜0,得：

解析：f'(x)=x2-a x+(a-1)。當f'(x)=0,解得x1=1或x2=a-1。

當a-1≤1,即a≤2時,x∈(1,+∞)時,f'(x)＞0,所以f(x)在(1,+∞)內遞增,不符合題意。

當a-1＞1,即a＞2時,x∈(1,a-1)時,f'(x)＜0;x∈(a-1,+∞)時,f'(x)＞0。

所以f(x)在(1,a-1)上遞減;在(a-1,+∞)上遞增。

又由已知得x∈(1,4)時,f'(x)＜0, x∈(6,+∞)時f'(x)＞0。

故4≤a-1≤6,即5≤a≤7。

2.求可導函數極值的步驟為：

①求導函數f'(x)。

②求方程f'(x)=0的根。

③檢查f'(x)在方程根左、右的符號,如果左正右負,那么f(x)在這個根處取得極大值;如果左負右正,那么f(x)在這個根處取得極小值,如果左右不改變符號即都為正或都為負,那么f(x)在這個根處無極值。

設x=1與x=2是函數f(x)= al nx+b x2+x的兩個極值點。

(1)試確定常數a和b的值;

(2)試分別判斷x=1,x=2是函數f(x)的極大值點還是極小值點,并說明理由。

(1)由極值點的必要條件可知：f'(1)= f'(2)=0,即a0。解方程組可得

變式3：已知函數f(x)=a x3+b x2+ c x,取得極小值-4,并且使其導數f'(x)＞0的x的取值范圍為(1,3),求f(x)的解析式。

解析：由題意得f'(x)=3a x2+2b x+ c=3a(x-1)(x-3),a＜0。

故在(-∞,1)上,f'(x)＜0;在(1,3)上, f'(x)＞0;在(3,+∞)上,f'(x)＜0。

因此,f(x)在x0=1處取得極小值-4。

故f(x)=-x3+6x2-9x。

3.利用導數求函數的最值時,首先求f(x)在[a,b]內的極值,然后將f(x)的各極值與f(a)、f(b)比較得出函數f(x)在[a,b]上的最值。具體可分為以下幾步：①求f'(x)=0的解x0;②用極值的方法確定極值;③將[a,b]內的極值與f(a),f(b)比較,其中最大的為最大值,最小的為最小值。

(1)當a=2時,求f(x)的極值;

(2)若不等式f(x)+3≥0對所有的實a數R恒成立,求a的取值范圍。

由f'(x)=0得x=±1,當x變化時f'(x)及f(x)的變化情況如表1：對所有的實數R均成立,即

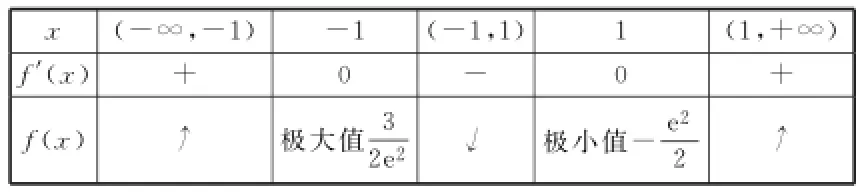
表1

令g'(x)=(x-1)(a x+2)eax=0,則時,g(x)取極大值x=1時,g(x)取極小值0,因而g(x)的最小值為

當

解得0＜a≤l n3。

變式4：已知函數f(x)=x3-a x2+3x。

(1)若f(x)在x∈[1,+∞)上是增函數,求實數a的取值范圍;

(2)若x=3是f(x)的極值點,求f(x)在x∈[1,a]上的最小值和最大值。

解析：(1)f'(x)=3x2-2a x+3,要使f(x)在x∈[1,+∞)上是增函數,則有3x2-2a x+3≥0在x∈[1,+∞)上恒成立,即a內恒成立。

(2)由題意知f'(x)=3x2-2a x+3=0的一個根為x=3,可得a=5。

所以f'(x)=3x2-1 0x+3=0的根為

又f(1)=-1,f(3)=-9,f(5)=1 5,故f(x)在x∈[1,5]上的最小值是f(3)= -9,最大值是f(5)=1 5。

三、利用導數證明等式或不等式

利用導數證明等式或不等式為高中數學引進了新的思路和方法,在證明不等式或等式成立時,先要構造函數和確定其定義域,再運用求導的方法來證明。已知函數f(x)=al nx-a x-3,a∈R。

(1)討論函數f(x)的單調性;

(2)若函數y=f(x)的圖像在點(2, f(2))處的切線的傾斜角為4 5°,對于任意的t∈[1,2],若函數g(x)=x3+x2·在區間(t,3)上總不是單調函數,求實數m的取值范圍;

(3)求證：l n(22+1)+l n(32+1)+ l n(42+1)+…+l n(n2+1)＜1+2 l nn!(n≥2,n∈N*)。

g'(x)=3x2+(m+4)x-2。

g'(0)=-2。

由題意知,對于任意的t∈[1,2],g'(t)

(3)令a=-1,此時f(x)=-l nx+x-3,所以f(1)=-2。

由(1)可知f(x)=-l nx+x-3在(1,+∞)上單調遞增,故當x∈(1,+∞)時f(x)＞f(1),即-l nx+x-1＞0,l nx＜x-1對一切x∈(1,+∞)成立。

若n≥2,n∈N*,則有

因l n(22+1)+l n(32+1)+l n(42+1)+…+l n(n2+1)＜1+2 l nn!(n≥2,n∈N*),可變形為l nN*),所以：

變式5：已知函數f(x)=ex-l n(x+1) -1(x≥0)。

(1)求函數f(x)的最小值;

(2)若0≤y＜x,求證：ex-y-1＞l n(x+1)-l n(y+1)。

則函數f(x)在0,+∞[)上單調遞增,函數f(x)的最小值為f(0)=0。

(2)由(1)知,當x＞0時,f(x)＞0。

因為x＞y,所以f(x-y)=ex-yl n(x-y+1)-1＞0。

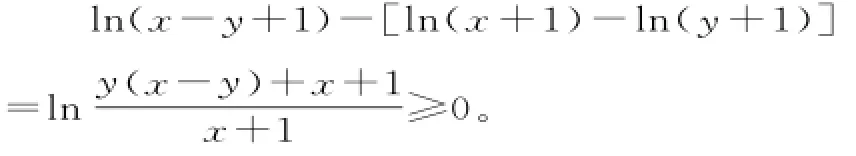
由①②可得：

ex-y-1＞l n(x+1)-l n(y+1)。

四、導數在實際問題中的運用

導數在自然科學、工程技術等方面都有廣泛的應用,解決實際應用問題關鍵在于建立數學模型和目標函數,把“問題情景”譯為數學語言,找出問題的主要關系,并把問題的主要關系近似化、形式化,抽象成數學問題,再歸為常規問題,選擇合適的數學方法求解。難點是如何把實際問題中所涉及的幾個變量轉化成函數關系式。煙囪向其周圍地區散落煙塵而造成環境污染。已知A、B兩座煙囪相距3k m,其中A煙囪噴出的煙塵量是B煙囪的8倍,經環境檢測表明：落在地面某處的煙塵濃度與該處到煙囪距離的平方成反比,而與煙囪噴出的煙塵量成正比(比例系數為k)。若C是連接兩煙囪的線段A B上的點(不包括端點),設A C=xk m,C點的煙塵濃度記為y。

(1)寫出y關于x的函數表達式。

(2)是否存在這樣的點C,使該點的煙塵濃度最低?若存在,求出A C的距離;若不存在,請說明理由。

解析：(1)設B處煙塵量為1,則A處煙塵量為8,故有A煙囪在C處的煙塵濃度為,B煙囪在C處的煙塵濃度為中0＜x＜3。

從而C處總的煙塵濃度為：

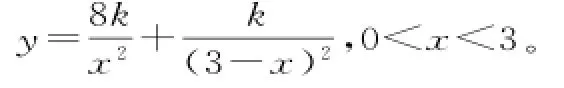
故當0＜x＜2時,y'＜0;當2＜x＜3時y'＞0。可見當x=2時,y取得極小值,且是最小值。

故在連接兩座煙囪的線段A B上,距煙囪A處2k m處的煙塵濃度最低。

變式6：在甲、乙兩個工廠,甲廠位于一直線河岸的岸邊A處,乙廠與甲廠在河的同側,乙廠位于離河岸4 0k m的B處,乙廠到河岸的垂足D與A相距5 0k m,兩廠要在此岸邊合建一個供水站C,從供水站到甲廠和乙廠的水管費用分別為每千米3a元和5a元,問供水站C建在岸邊何處才能使水管費用最省。

設總的水管費用為f(θ),依題意有：

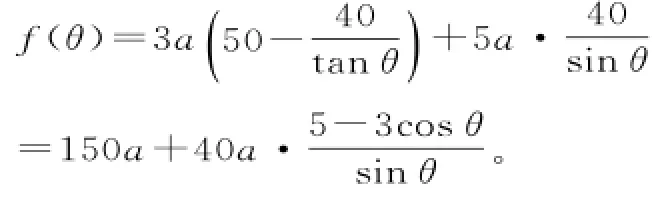
導數既是新課程的新增內容,又是函數、解析幾何的交匯點,是同學們今后學習的基礎,起著重要的工具作用,豐富了對函數研究的方法,現在已是新高考重點考查的基礎知識,成為高考數學的一大熱點,相信在今后的高考中仍然會重點考查,所以同學們一定要給予高度重視。

(責任編輯 徐利杰)