定積分的幾類應用
定積分的幾類應用
■江西省井岡山中學 賀 敬
定積分的應用是我們學習的重點內容,那么定積分究竟有哪些應用呢?下面我們進行歸納總結。
一、解決面積的求法
分析:可先畫出圖形,找出范圍,用積分表示,再求積分值。
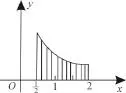
圖1
點評:求平面圖形的面積,首先要畫出平面圖形,然后根據圖形的特點,選擇相應的積分變量以確定積分區間,寫出面積的積分表達式,再進行求解。
二、解決路程問題
一質點在直線上從時刻t=0(s)開始以速度v=t2-4t+3(m/s)運動,求:
(1)在t=4s的位移;
(2)在t=4s運動的路程。
分析:將區間[0,4]等分成n個小區間,在每個小區間[x,x+Δ x]上,當Δ x非常小時,可以近似看成勻速直線運動,當n無限大時,在t=4s位置就是v(t)在[0,4]上的定積分,而路程就是位移的絕對值之和。
解:(1)在時刻t=4s時,該點的位移為:
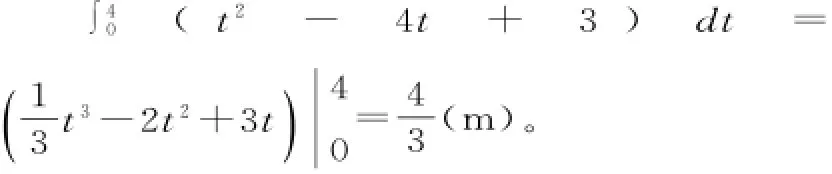
(2)v(t)=t2-4t+3=(t-1)(t-3),故在區間[0,1]及[3,4]上v(t)≥0,在區間[1, 3]上,v(t)≤0。
所以在t=4s時的路程為:
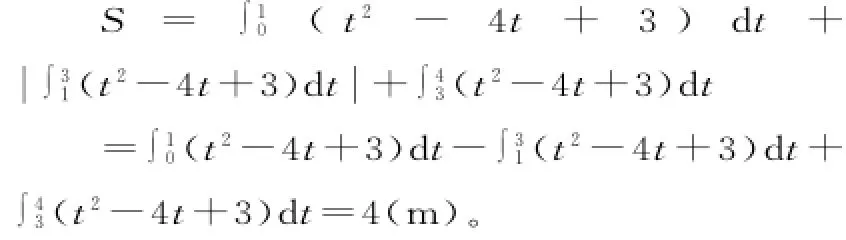
點評:由積分思想可知,做變速直線運動的物體所經過的位移,等于其速度函數v= v(t)在時間區間[a,b]上的定積分,而路程是位移的絕對值之和,故求路程要判斷速度的符號。
三、解決變力做功問題
直徑為2 0c m,高為8 0c m的圓柱體內充滿壓強為1 0N/c m2的蒸氣,設溫度保持不變,要使蒸氣的體積縮小為原來的一半,則需要做的功是_____。
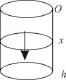
圖2
分析:對變力F進行定積分,即可得變力所做的功。
解:設上端為活塞,且如圖2所示取定x軸。另設底面面積為S,活塞壓縮至x位置時氣體的體積為V(x),壓強為P(x),由于P V=k(其中k為常數),則:
故所做的功為:
點評:求變力做功問題,一般利用定積分加以解決,要注意尋找積分變量與積分區間。
(責任編輯 徐利杰)
- 中學生數理化(高中版.高二數學)的其它文章
- 有機化學專項訓練(二)
- 解讀烴和鹵代烴知識考查熱點
- 烴類易混淆點突破
- 烴類高考常見考點直擊
- 電磁感應綜合應用檢測題
- 電磁感應新穎試題賞析

