一種全地形車橡膠扭力軸套扭轉剛度建模及優化方法

姚壽文，鄭 鑫，程海濤，黃友劍，莫容利 Yao Shouwen，Zheng Xin，Cheng Haitao，Huang Youjian，Mo Rongli

?

一種全地形車橡膠扭力軸套扭轉剛度建模及優化方法

姚壽文1，鄭 鑫1，程海濤2，黃友劍2，莫容利2Yao Shouwen1，Zheng Xin1，Cheng Haitao2，Huang Youjian2，Mo Rongli2

（1. 北京理工大學 機械與車輛學院，北京 100081；2. 株洲時代新材料科技股份有限公司，湖南 株洲 412007）

橡膠扭力軸套具有體積小、重量輕等優點，逐漸取代扭桿等傳統懸架形式在全地形履帶車中得以應用。扭力軸套的扭轉剛度決定了懸架的減振性能，進而影響整車平順性表現，目前尚缺乏從全地形車整車平順性角度出發的扭轉剛度模型。結合橡膠扭力軸套懸架結構特點，從橡膠元件的非線性特性出發建立扭轉剛度的理論模型，并結合整車動力學模型，以路面不平度作為激勵輸入計算平順性指標，建立扭轉剛度參數的響應面模型并進行優化。優化后的扭轉剛度模型提高了全地形車的平順性，為全地形履帶車橡膠扭力軸套的扭轉剛度特性設計提供了理論依據。

橡膠扭力軸套；扭轉剛度模型；動力學建模；平順性；優化

0 引 言

全地形車（All-Terrain Vehicle，ATV）是指可以在任何地形上行駛的車輛，較之普通車輛，其最大的特點是接地比壓低、通過能力強且具有良好的地形適應能力。瑞典、芬蘭及蘇聯等國家出于在惡劣地形條件下運輸物資的需要，于20世紀70年代開始全地形車的研究，而目前國內對于全地形車輛的研究還處于起步階段[1]。全地形車主要分為履帶式全地形車、輪式全地形車和輪履合一輕型全地形車3種，其中履帶式全地形車由于具有更好的通過性和運載能力，在軍事、農業以及灘涂運輸等領域獲得廣泛的應用[2]。

為實現車體減重，順利通過雪地、沼澤等地形以及實現兩棲行駛，全地形履帶車在懸架系統中采用了體積小、重量輕的橡膠扭力軸套作為減振元件。與傳統的扭桿等形式的懸架相比，該種懸架能夠有效減小行駛系統的質量，從而降低接地比壓，提升離地間隙，提高通過性能。在這種懸架類型中，橡膠扭力軸套的扭轉剛度特性是影響懸架減振及整車平順性的關鍵因素。目前，針對橡膠扭力軸套扭轉剛度特性開展的研究較少，沒有建立橡膠扭力軸套剛度特性設計的理論模型。

以某全地形履帶車所采用的橡膠扭力軸套為研究對象，結合橡膠扭力軸套的非線性特點，提出一種扭轉剛度理論模型。在此模型的基礎上，從全地形履帶車整車平順性評價的角度出發，利用多體動力學軟件建立整車模型并進行平順性仿真，以車身垂向加權加速度均方根值為優化目標，確定優化參數取值范圍，應用中心復合法設計優化仿真試驗，建立響應面預測模型，獲得平順性表現最優的橡膠扭力軸套扭轉剛度模型。

1 軸套扭轉剛度建模

綜合考慮橡膠扭力軸套扭轉剛度的非線性特點和全地形履帶車平順性的要求，首先建立表達垂向力與扭力軸套扭轉角度的描述方程，以此為基礎等效推導扭力軸套扭轉剛度的非線性模型，并對模型中的參數進行定性分析。

某全地形履帶車所采用的橡膠扭力軸套懸架結構如圖1所示，平衡肘的端與橡膠扭力軸套的內緣相固連，平衡肘端與負重輪相連，平衡肘長度為，0為安裝位置與水平線的夾角，為負重輪受力之后平衡肘扭轉的角度，規定以逆時針為正。

全地形履帶車輛行駛過程中，地面對履帶的作用力通過負重輪傳遞到平衡肘，平衡肘在受到垂向力時，平衡肘端從初始位置起轉動角度，則由扭矩平衡可得

式中，K為橡膠扭力軸套的扭轉剛度。

則垂向力的表達式為

負重輪垂向行程可由幾何關系得到

（3）

垂向力對垂向位移求微分，得到懸架的等效剛度為

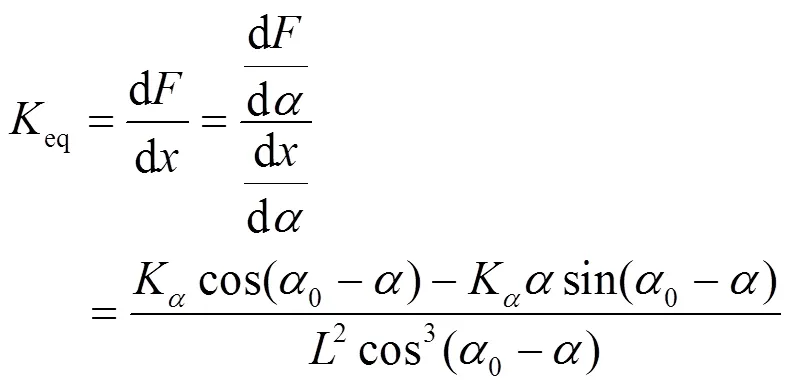
由式（4）可以發現，在懸架結構參數確定的情況下，該懸架的等效剛度特性取決于橡膠扭力軸套的扭轉剛度K。

橡膠元件呈現明顯的非線性特征，目前具有非線性特性的系統模型種類繁多，如死區非線性、飽和非線性和間隙非線性等，與大多車輛懸架系統彈性元件的特性差別較大。從全地形履帶車平順性評價的角度而言，要想取得理想的平順性表現，懸架在小行程下應具有較小的剛度，以隔絕高頻、小幅振動獲得良好的舒適性；在大行程下應具有較大的剛度，防止負重輪行程過大對車身產生沖擊。為滿足這一特點，采取指數形式建立垂向位移與垂向力的關系。根據方程指數的取值不同，方程呈現不同程度的非線性特征，定義該指數為非線性指數。在橡膠扭力軸套安裝時，預先有初始扭轉角度以保證一定的履帶張緊力，該預緊力的大小在方程中采用預緊系數來體現。為方便指數函數的進一步處理，同時減弱垂向力的非線性程度，定義衰減系數對垂向位移去量綱化。綜上，垂向力與垂向位移的關系式為

式中，為預緊系數，為衰減系數，為非線性指數。

將式（3）代入式（5），轉化為垂向力與扭轉角度的關系

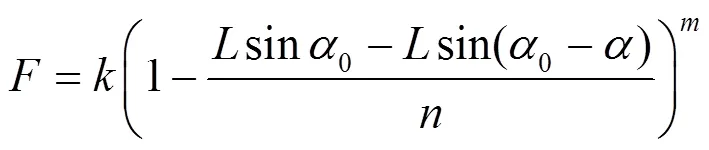
將式（6）代入式（2），得到扭力軸套的扭轉剛度

（7）

采用隔離變量的方法分別考察扭轉剛度模型中、、3個參數對扭轉剛度模型特性的影響。

固定衰減系數及非線性指數，對預緊系數取不同的值，得到扭轉剛度與扭轉角度的關系如圖2所示，由曲線可知，預緊系數只影響曲線的截距，即初始預緊力的大小；值越大，初始預緊力越大。預緊系數對模型的非線性程度不產生影響。

固定預緊系數及非線性指數，對衰減系數取不同的值，得到扭轉剛度與扭轉角度的關系如圖3所示，由曲線可知，衰減系數影響模型的非線性程度，的取值越大，對模型非線性產生的衰減越大，即模型的非線性程度越小。

固定預緊系數及衰減系數，對非線性指數取不同的值，得到扭轉剛度與扭轉角度的關系如圖4所示，由曲線可知，非線性指數影響模型的非線性程度，的絕對值越大，模型的非線性程度越大。

2 平順性仿真及評價

為了獲得扭轉剛度模型參數優化評價指標，以標準路面不平度作為激勵輸入，建立整車動力學模型，提取垂向加速度時間歷程進行統計分析，獲得垂向加權加速度均方根值。

2.1 路面不平度的生成

路面不平度可以由實際道路試驗測試或由給定功率譜密度變換為路面不平度兩種途徑獲得，后者在車輛動力學仿真研究中獲得了廣泛的應用[3]。

根據ISO提出的“路面不平度表示方法草案”，路面功率譜密度G()的擬合表達式為

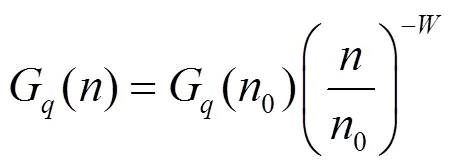
式中，為空間頻率，m-1，且>0；0為參考空間頻率，00.1 m-1；G(0)為參考空間頻率0下的路面功率譜密度值，m3；為頻率指數，一般取=2。

按路面功率譜密度把路面的不平程度分為8級，針對全地形車的行駛環境，仿真中取F級路面為試驗路面考察車輛的平順性能，F級路面功率譜密度G(0)=1.6384×10-2m3。采用基于諧波疊加法思想的功率譜逆變換函數生成標準級別路面不平度，數學模型可表達為

式中，A2=2G(f)?f，其物理含義為?f區間內所對應的功率值，將個正弦函數疊加之后得到的就是時域內的隨機路面不平度輸入。

利用式（9）模擬得到的F路面不平度如圖5所示。

2.2 動力學建模與仿真

研究扭力軸套扭轉剛度模型對懸架特性及整車平順性的影響，與其關系較小的車體附件及防護裝甲的質量均等效為車體質量，車體整體視為剛體，以質量及轉動慣量的形式參與動力學建模[4-5]。

全地形履帶車行駛系統的多剛體模型如圖6所示，主要包括履帶、主動輪、負重輪、誘導輪、托帶輪及平衡肘等部件，在相應部件之間添加約束，根據動力系統的參數將動力施加于主動輪上。將橡膠扭力軸套扭轉剛度的理論模型曲線離散為數據點導入懸架模型中。對于全地形車所采用的整體式橡膠履帶，采取離散化思路，將整體式履帶等效離散為履帶板的連接，在履帶板之間建立柔性力約束，引入履帶的縱向拉伸剛度和彎折剛度，模擬橡膠履帶在行進過程中的拉伸和彎折效應。

該全地形履帶車設計參數：滿載質量6.9 t，整備質量6.3 t。輪系的主要參數見表1。將前面數值模擬獲得的路面不平度轉換為路面文件導入到多剛體模型中，按照該全地形履帶車的陸上常規車速30 km/h設置仿真車速，提取車體質心處的垂向加速度時間歷程()進行平順性評價。

表1 輪系主要設計參數

名 稱數量n/個質量m/kg半徑r/mm 主動輪110.8220 負重輪5 7.8210 托帶輪2 2.5100 誘導輪1 7.8210

2.3 平順性評價方法

根據ISO 2631-1: 1997標準，對于車輛正常行駛工況（包括越野工況），可采用加權加速度均方根值來評價振動對人體舒適和健康的影響。采用該方法時，先計算各軸向加權加速度均方根值，然后對加速度時間歷程()通過頻率加權函數()的濾波網絡得到加權加速度時間歷程w()[6-7]，由式（10）得到加權加速度均方根值

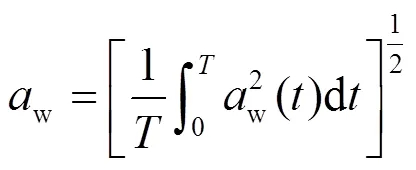
在正常行駛情況下，履帶車輛左右兩側履帶歷經的路面基本對稱，車體質心的振動主要是沿垂直方向的振動，因此以垂向加權加速度均方根值為評價指標。垂向加速度的頻率加權函數k()可表達為

（11）

式中，為頻率，Hz。對記錄的加速度時間歷程()進行頻譜分析得到功率譜密度函數G()，并按式（12）進行計算。

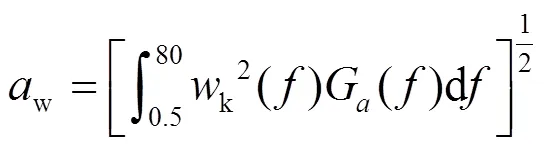
3 基于響應面的剛度模型優化

橡膠扭力軸套扭轉剛度模型中、、3個參數的變化，在路面的激勵下通過行駛系統及車體這個復雜系統表現為垂向加速度的變化，因此橡膠扭力軸套扭轉剛度模型的優化是一個三因子、單目標的優化問題，處理此類優化問題，如果采用每次仿真試驗改變一個因子的方法，將使計算成本激增，計算效率低下，同時也容易忽略各影響因子之間的交互作用[8-9]。響應面法(Response Surface Meth- odology，RSM)[10]應用統計的方法，將輸入激勵的變動和系統的不確定性納入優化過程，可以快速獲得主要影響因子及各因子之間的交互作用，并獲得系統響應面及擬合后的曲面方程，獲得最優解[11]，適合于本次模型的優化。

采用含交叉項的二次型構造響應面函數，則有

響應面模型的預測能力取決于響應面函數對試驗數據擬合的近似程度，以復相關系數2為評價指標，該值越接近1說明誤差的影響越小，復相關系數

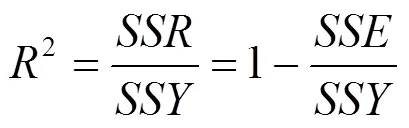
式中，為響應值與響應均值差的平方和，為響應值與響應估計值差的平方和，為響應估計值與響應均值差的平方和，分別為

（15）

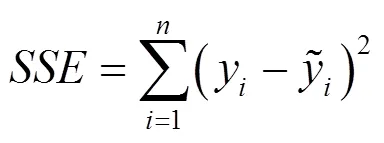
（17）

3.1 仿真試驗設計

在橡膠扭力軸套扭轉剛度模型中，、、3個參數為優化模型自變量，參考實際扭轉試驗獲得的扭轉剛度大小，同時綜合考慮車體自重及工程實際，確定優化變量的取值范圍為6 500≤≤10 500，0.30≤≤0.60，-3≤m≤-1，該優化問題可以描述為

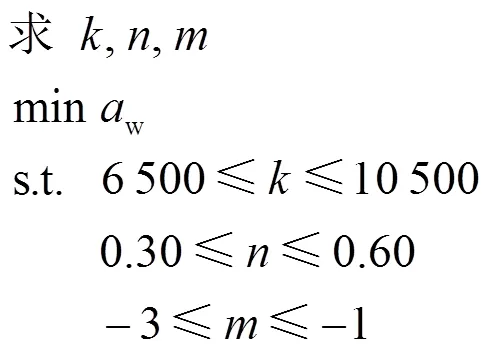
仿真試驗點的選取按照中心復合設計（Central Composite Design，CCD）進行選取，中心復合設計由Box和Wilson于1951年提出[12]，將傳統的差值點分布方式與全因子或部分因子設計相結合，是目前應用最為廣泛的二次響應面試驗點設計方法[13]。按照中心復合設計方法設計了20次仿真試驗，其中析因部分試驗（Factorial）8次，軸點部分試驗（Axial）6次，為保證均一精密性，中心點（Center）重復試驗6次，各仿真試驗點影響因子的取值見表2。

按照中心復合設計得到的仿真試驗點，改變動力學模型中的相應影響因子數值，進行仿真計算并對平順性進行評價，獲得垂向加權加速度均方根值w作為響應值，見表2。

表2 中心復合設計仿真試驗點及響應值

序號類型knmaw/(m/s2) 1Axial5 136.410.45-2.004.019 7 2Center8 5000.45-2.003.312 7 3Factorial6 5000.60-1.007.092 4 4Center8 5000.45-2.003.330 6 5Factorial10 5000.60-3.005.762 4 6Axial8 5000.45-0.326.512 9 7Axial8 5000.20-2.0010.690 1 8Center8 5000.45-2.003.297 8 9Center8 5000.45-2.003.265 4 10Factorial6 5000.60-3.004.664 2 11Center8 5000.45-2.003.380 1 12Factorial10 5000.30-1.003.461 9 13Axial8 5000.45-3.687.571 8 14Factorial10 5000.30-3.0011.370 6 15Factorial6 5000.30-1.003.607 6 16Axial8 5000.70-2.005.261 4 17Factorial10 5000.60-1.005.601 9 18Factorial6 5000.30-3.009.129 4 19Axial11 863.590.45-2.005.031 8 20Center8 5000.45-2.003.287 3

3.2 響應面分析

采用含交叉項的二次型構造加權加速度均方根值響應面函數

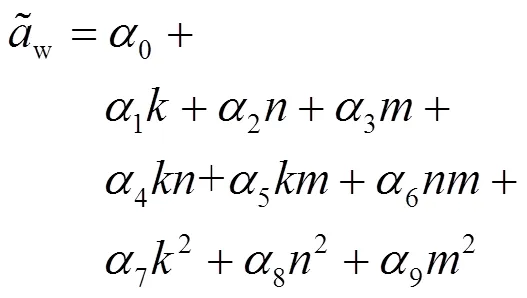
式中，α(=0~9)為各項的待定系數。

利用Design Expert軟件對仿真試驗獲得的加速度數據進行處理分析，求解響應面函數中的待定系數，獲得回歸方程預測模型中的各項系數見表3。

該預測模型的復相關系數2=0.934 0，說明該響應面模型可以較好地對仿真試驗數據進行二次擬合，具備一定的預測能力。

表3 回歸方程預測模型中各項系數

系數取值系數取值 α018.322 8α5-3.110 9×10-3 α1-1.520 3×10-3α613.083 3 α234.462 2α7 8.758 6×10-8 α3 0.769 5α869.782 4 α4-1.035 8×10-3α9 1.240 1

為方便比較各因子影響效應的大小，對各影響因子的取值進行歸一化處理，處理之后的回歸方程預測模型中的各項系數見表4，響應面等高線圖如圖7～9所示，顯示了預緊系數、衰減系數和非線性指數的交互作用對響應值的影響。

表4 歸一化后的回歸方程預測模型中各項系數

系數取值系數取值 α0 3.32α5-0.62 α1 0.25α6 1.96 α2-0.99α7 0.35 α3-0.95α8 1.57 α4-0.31α9 1.24

預緊系數和衰減系數對響應值的交互影響作用，由等高線圖可以得出，如圖7所示，衰減系數對預測模型的影響較預緊系數要顯著。

預緊系數和非線性指數對響應值的交互影響作用，由等高線圖可以得出，如圖8所示，非線性指數對預測模型的影響較預緊系數要顯著。

衰減系數和非線性指數對響應值的交互影響作用，由等高線圖可以得出，如圖9所示，衰減系數對預測模型的影響較非線性指數要顯著。

由圖7～9比較可得，對平順性產生最主要影響的因素是衰減系數，其次為非線性指數和預緊系數，體現在預測方程中的一次項及二次項的系數上為|2|>|3|>|1|，|8|>|9|>|7|。由響應面等高線圖可以發現預測模型存在極值，即等高線的圓心處，從而得到模型的最優解為=8 349.12，=0.47，=-1.76，此時預測響應值為3.122 97 m/s2。

將最優解下的橡膠扭力軸套扭轉剛度模型與扭轉試驗獲得的產品扭轉剛度特性相對照，如圖10所示。由圖中曲線可以發現，優化后的扭轉剛度與試驗測得曲線相比，非線性程度加強。將試驗曲線導入整車模型進行仿真計算，得到的垂向加權加速度均方根值為3.463 7 m/s2，與最優解的預測響應值相比，優化之后的模型垂向加速度降低了9.84%，說明應用優化模型之后的全地形履帶車整車平順性得到了提升。

4 結 論

1）從全地形履帶車懸架結構出發，綜合考慮橡膠扭力軸套的非線性特點及整車平順性要求，建立了扭轉剛度的理論模型，并對影響模型數學特征的3個參數進行定性分析。

2）建立全地形車整車動力學模型，并將橡膠扭力軸套扭轉剛度理論模型應用到行駛系統建模當中，以柔性連接力模擬橡膠履帶的特性，采用F級標準路面不平度作為輸入進行動力學仿真計算，得到車體垂向振動加速度。

3）以扭轉剛度模型中的參數作為優化變量，以仿真計算得到的整車垂向加權加速度均方根值作為輸出，建立響應面預測模型對扭轉剛度特性進行優化，在設計可行域內得到滿足約束要求的優化解。與實際扭轉剛度特性相比，優化后的模型提高了車輛的平順性，為后續不同車型及結構參數下扭力軸套扭轉剛度設計提供了一定的理論依據。

[1]馮付勇，洪萬年，張勇. 雙節全地形履帶車輛發展探討[J]. 車輛與動力技術，2011（3）：57-60.

[2]左鵬，成凱，周怡澤. 全地形鉸接履帶運輸車扭桿彈簧的研究[J]. 機械設計，2011，28（8）：12-16.

[3]劉輝，符升平，項昌樂. 不平整路面履帶車輛動力傳動系統扭轉隨機激勵研究[J]. 農業機械學報，2010，41（12）：1-6.

[4]馮金芝，劉樂，鄭松林. 某轎車懸架系統的載荷仿真分析[J]. 汽車工程，2012，34（10）：913-917.

[5]管欣，吳振昕，詹軍. 用于汽車動力學實時仿真的懸架建模方法的研究[J]. 汽車工程，2007，29（5）：433-436.

[6]余志生. 汽車理論[M]. 北京：機械工業出版社，2005.

[7]趙六奇，劉鋒. 參照國際標準ISO 2631的新草案修訂汽車平順性的評價方法[J]. 汽車工程，1993（6）：371-377.

[8]芮強，王紅巖. 基于響應面法的懸架系統優化研究[J]. 裝甲兵工程學院學報，2006，20（4）：49-52.

[9]潘鋒，朱平. 面向約束優化的改進響應面法在車身輕量化設計中的應用[J]. 機械工程學報，2011，47（10）：82-87.

[10]Hill W J, Hunter W G. A Review of Response Surface Methodology: A Literature Survey[J]. Technometrics, 1966, 8(4): 571- 590.

[11]Pratheepa B. Modeling and Simulation of Automobile Suspen- sion System[J]. Frontiers in Automobile & Mechanical Engineering, 2010: 377-382.

[12] Box G E P, Wilson K B. On the Experimental Attainment of Optimum Conditions [J]. Journal of the Royal Statistical Society, 1951, 13 (1): 1-45.

[13]Picheny V, Kim N H, Haftka R T. Application of Bootstrap Method in Conservative Estimation of Reliability with Limited Samples[J]. Structural and Multidisciplinary Optimization, 2009, 41(2): 205-217.

2014-07-01

1002-4581（2017）02-0005-07

U463.33+4

A

10.14175/j.issn.1002-4581.2017.02.002

校企聯合項目（JSGLC12012002）。