三次樣條插值在通信工程中的應用

索昂代吉

（青海省無線電管理辦公室玉樹管理處，青海 玉樹 815000）

三次樣條插值在通信工程中的應用

索昂代吉

（青海省無線電管理辦公室玉樹管理處，青海 玉樹 815000）

在通信工程實踐中，經常會遇到離散測量數據的擬合問題，即用已知的有限樣本估計一些缺失的未知樣本，這時就需要借助插值運算。通過對三次樣條插值算法進行研究，將其應用至自由空間損耗計算、饋線插入損耗估計、相關干涉測向3個方面，并通過仿真驗證三次樣條插值算法在通信工程應用中的有效性。

三次樣條插值；自由空間傳輸損耗；饋線插入損耗；相關干涉測向

1 引言

通信工程實踐中，經常遇到離散數據的采樣問題，有時因為所涉及的樣本較多，會有一部分有用樣本未被采集到。一種方法是在采樣時盡可能多地將所需樣本全部采集到，這種方法得到的數據結果較為準確，但是測量時間較長，導致工作效率降低；另一種方法是用采集到的已知樣本來完成一些未知所需樣本的計算。而插值作為一種數值逼近的重要方法，可以通過有限個樣本的取值情況估計出未知樣本的近似值。

目前常見的插值算法有拉格朗日插值、牛頓插值、厄米特插值、樣條插值等。前3種插值方式均為線性插值，線性插值計算簡單穩定，但是其插值誤差較大，而且光滑性較差[1]。因此需要一種更好的插值算法，既有線性插值的優點，又能保證插值精度，使得插值得到的數據和真實數據的誤差都在合理范圍內，三次樣條插值就可以滿足上述需求。而且，近年來三次樣條插值也已廣泛應用至通信領域，參考文獻[2]提出將經典對數距離衰減模型中的衰減因子由距離和信號強度的三次樣條插值函數代替，在不增加參數的情況下減少模型誤差，在指紋識別法校準階段僅對有限位置的信號強度進行采集，通過衰減模型估計其他位置的信號強度，進而減少校準工作量。參考文獻[3]提出將三次樣條插值應用于WCDMA移動終端中功率放大器（PA）的校準過程中，通過測量少量采樣點配合三次樣條插值得到PA的功率曲線。參考文獻[4]提出了一種基于三次樣條插值的改進去噪算法，利用Ad Hoc算法搜索信號產生模極大值點，形成模極大值線，對于保留下來的模極大值點進行三次樣條插值，得到信號的估計小波系數，進而用估計小波系數重構原始信號，達到濾波去噪的目的。除通信領域外，三次樣條插值在其他領域也有較廣泛的應用，如風洞試驗[5]、電力系統信號采樣重構[6]等。

2 三次樣條插值

數學中的樣條 （spline）一詞來源于它的直觀幾何背景，繪圖員或鈑金工人常用彈性木條或金屬條加壓鐵（構成樣條）固定在樣點上，在其他地方讓它自由彎曲，然后畫下長條的曲線，稱為樣條曲線。樣條曲線實際上是由分段三次曲線拼接而成，在連接點上要求二階導數連續，從數學上加以概括就得到數學樣條這一概念。

2.1 三次樣條插值的函數定義[1]

給定區間[a,b]上的各節點a=x0＜x1＜…＜xn=b和這些節點上的函數值f(xi)=yi(i=0,1,…,n)，若S(x)滿足：

·S(xi)=yi(i=0,1,…,n)；

·S(x)在每一個小區間[xi,xi+1](i=0,1,…,n-1)上是次數小于或等于3的多項式；

·S(x)，S′(x)，S″(x)在[a,b]上連續。

則稱S(x)為函數f(x)關于節點x0,x1,…,xn的三次樣條插值函數。分段三次樣條插值曲線如圖1所示。

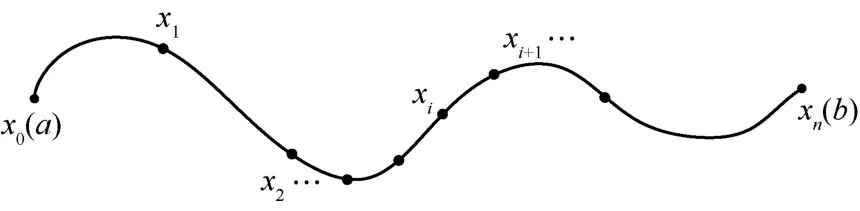
圖1 分段三次樣條插值曲線

從定義可知，要求出S(x)，在每個小區間[xi,xi+1]上要確定4個待定系數，共有n個小區間，故應確定4n個參數。

根據S(x)在[a,b]上二階導數連續，在節點xi(i=1,2,…, n-1)處應滿足連續性條件：

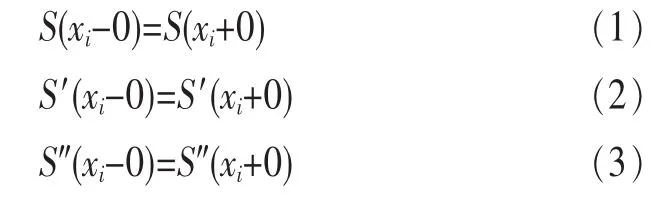
共有3(n-1)=3n-3個條件，再加上S(x)滿足插值條件S(xi)=yi(i=0,1,…,n)，總共有3n-3+n+1=4n-2個條件，因此還需要2個條件才能確定S(x)。

通常可在區間[a,b]端點a=x0,b=xn上各加一個條件（稱為邊界條件），可根據實際問題的要求給定，常見的有以下3種：

·已知兩端的一階導數值，即S′(x0)=f0′，S′(xn)=fn′（固支邊界）；

· 已知兩端的二階導數值，即 S″(x0)=f0″，S″(xn)=fn″，（簡支邊界），特殊情況為S″(x0)=S″(xn)=0（自然邊界條件）；

· 當f(x)是以xn-x0為周期的周期函數時，則要求S(x)也是周期函數，這時邊界條件應滿足：

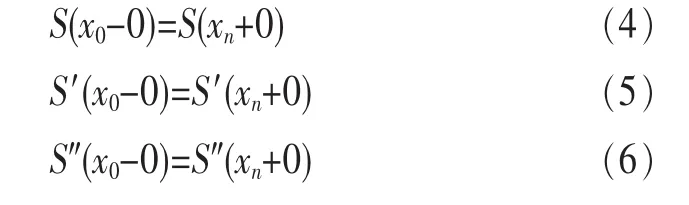
而此時y0=yn，這樣確定的樣條函數S(x)稱為周期樣條函數。

2.2 三彎矩算法

三次樣條插值函數S(x)可以有多種表達式，有時用二階導數值S″(x)=Mi(i=0,1,…,n)表示時，使用更為方便。Mi在力學上解釋為細梁在xi處的彎矩，并且得到的彎矩與相鄰兩個彎矩有關，故稱用Mi表示S(x)的算法為三彎矩算法。

由于S(x)在區間[xi,xi+1]上是三次多項式，故S′(x)在[xi, xi+1]上是線性函數，可表示為：

對式（7）進行積分，得：

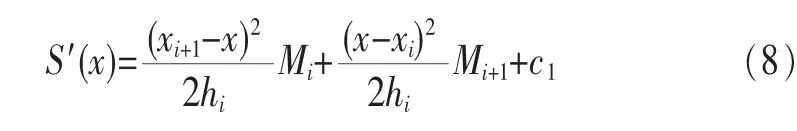
再積分得：

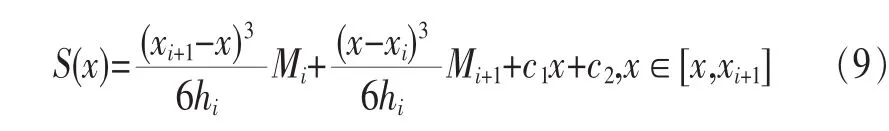
由條件S(xi)=yi、S(xi+1)=yi+1確定積分常數c1、c2：

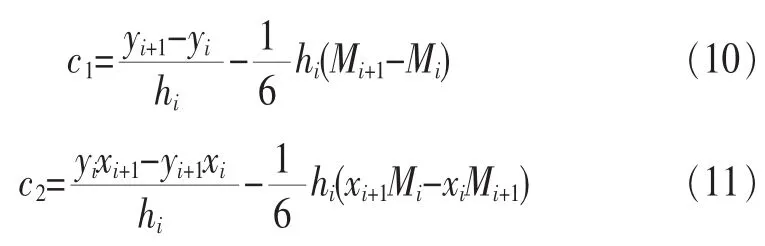
將c1、c2代入三次樣條插值函數S(x)的表達式中，可知，只要確定Mi(i=0,1,…,n)這n+1個值，就可定出三次樣條插值函數S(x)。

為了確定Mi(i=0,1,…,n)的值，對S(x)求導得：

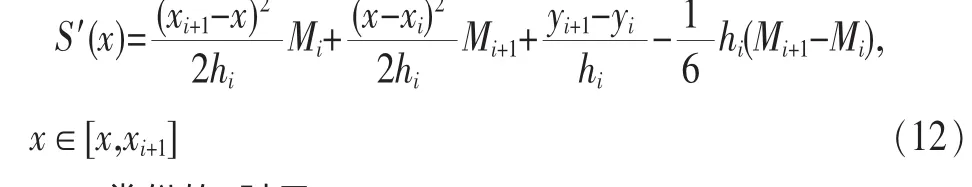
類似的，對于 x∈[xi-1,xi]：

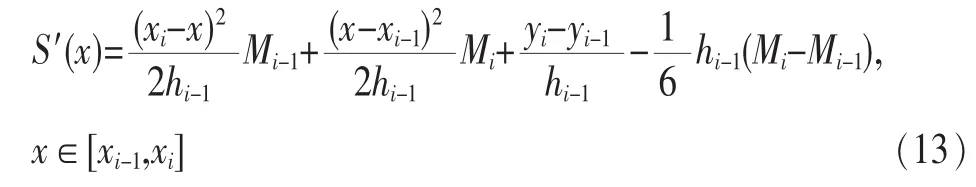
應用導數連續條件S′(xi-0)=S′(xi+0)：

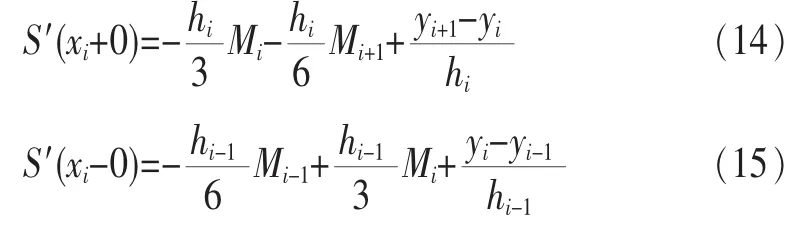
利用 S(x)在內接點的連續性，即 S′(xi-0)=S′(xi+0)可得：

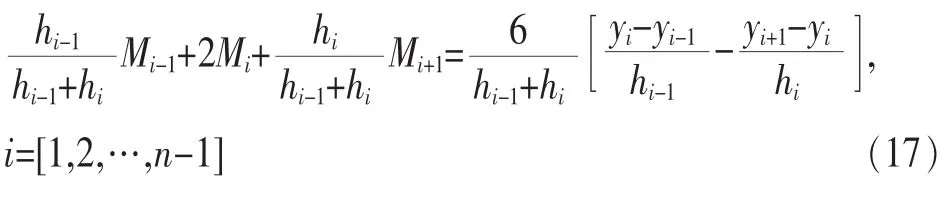
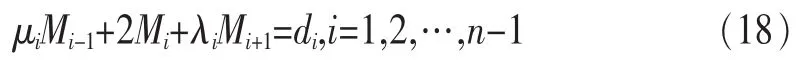
此方程組即三彎矩方程。這是一個含有n+1個未知數、n-1個方程的線性方程，要完全確定Mi(i=0,1,…,n)的值還需要補充兩個條件，這兩個條件通常根據實際問題的需要，根據插值區間[a,b]兩個端點處的邊界條件來補充。

（1）已知兩端點的一階導數值S′(x0)=f0′，S′(xn)=fn′

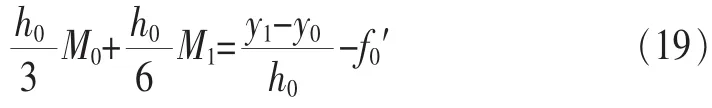
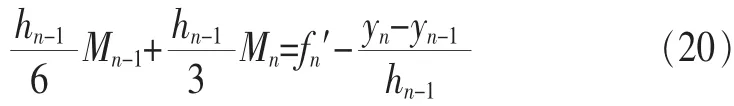
整理式（19）、式（20）得：

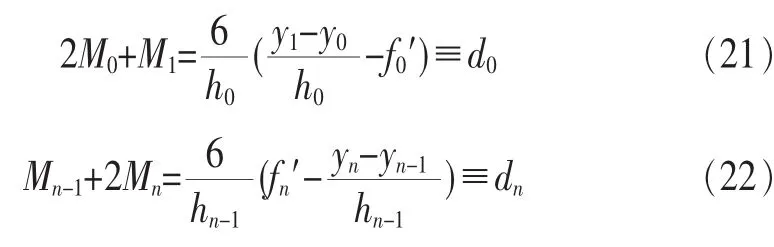
令λ0=1，μn=1，得到Mi(i=0,1,…,n)滿足的方程組為：

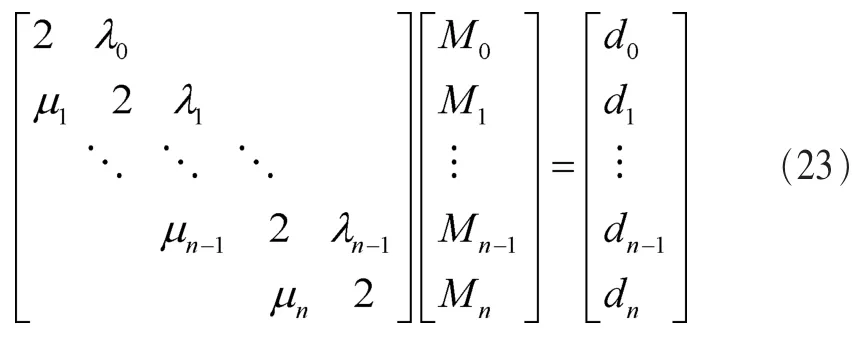
（2）已知兩端點的二階導數值S″(x0)=M0=f0″，S″(xn)=Mn=fn″代入方程（17），只需解n-1個方程，即：

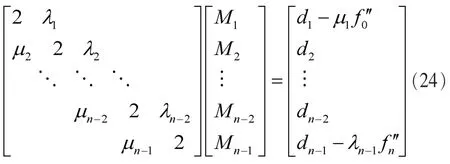
（3）第三類邊界條件S′(x0+0)=S′(xn-0)，S″(x0+0)=S″(xn-0)

由式（14）、式（15）及邊界條件 S′(x0+0)=S′(xn-0)可得：

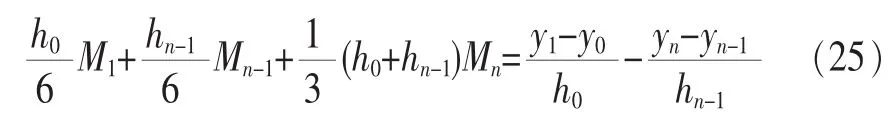
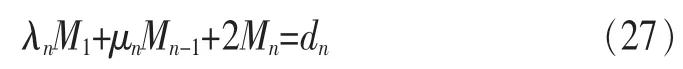
又由M0=Mn，三彎矩方程可寫為：

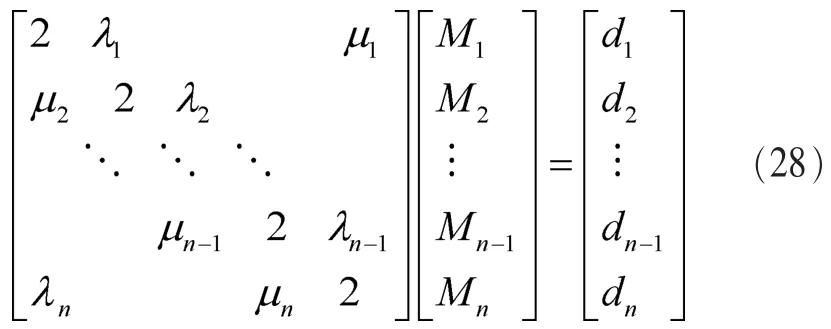
式（23）、式（24）、式（28）系數矩陣都是嚴格對角占優矩陣，因此式（23）、式（24）、式（28）有唯一解，可用追趕法進行求解。

3 三次樣條插值在通信工程中的實際應用

選取3個典型實例對三次樣條插值在通信工程中的應用來進行驗證，并將三次樣條插值的結果和線性插值、分段三次厄米特插值算法作對比，以下試驗均在國家無線電頻譜管理研究所的幫助下完成。

3.1 試驗1

在此用自由空間傳播損耗[7]作為例子來說明三次樣條插值。自由空間傳播損耗L0是用在自由空間中兩個理想點源天線（增益系數G=1的天線）之間的傳播損耗來定義的，它表示在自由空間中，當發射天線與接收天線的增益系數GT=GA=G時，發射天線的輸入功率（發射功率）與接收天線的輸出功率（接收功率）之比，即：

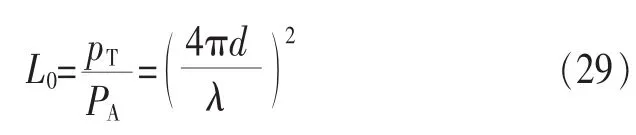
若以分貝表示：

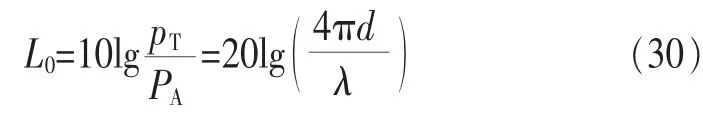
或：

其中，f為工作頻率，d為傳播距離。

在試驗中，固定f=5 MHz，觀察L0隨距離d的變化情況，取6個插值點來進行試驗，見表1。圖2、圖3分別給出了不同插值算法的插值結果及誤差。

表1 試驗中所選取的6個插值點

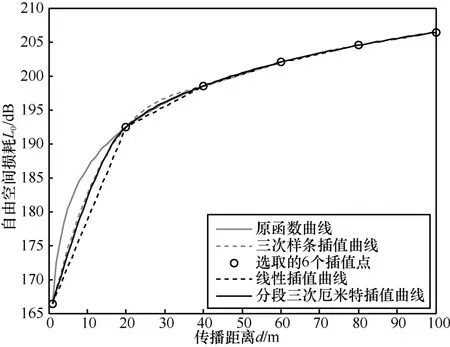
圖2 3種插值算法插值結果

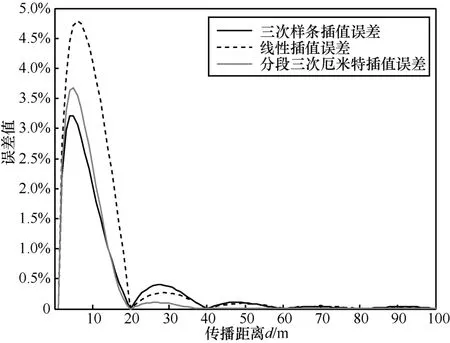
圖3 3種不同插值算法的插值誤差

從上述結果可以看出，三次樣條插值要明顯優于線性插值，和分段三次厄米特插值的插值結果不相上下，但是在兩個插值點之間斜率較大時，三次樣條插值的結果仍要優于分段三次厄米特插值。

3.2 試驗2

在實際工作中，經常需要對已有的饋線插入損耗值進行測試，為了減少測試人員的工作量，可以在測試時選取少量的測試點，然后再采用插值的方法獲得饋線在未測頻點處的插損值。在本次試驗中，首先利用標網測量實際在使用的一根金波DC-26.5 GHz低損耗饋線，得到一組原始測試數據，然后從這一組原始數據中選取11個插值點進行插值運算，得到3組不同的插值結果，見表2，其中為選擇的11個插值點。3種插值算法的插值誤差如圖4所示。

從以上結果中可以看出，采用插值方法對饋線插損值進行插值時，在低頻段處插值誤差較大，高頻點處的計算值則可以滿足實際需求，因此在使用時，可以將低頻點的測試步進選擇得盡可能小，高頻點處就可以相對選擇得稀疏一些。對比3種插值算法，三次樣條插值得到的插值結果相對來說誤差較小，更適合實際應用。

3.3 試驗3

在相關干涉測向中，需要在設計的天線陣列工作頻率范圍內，按一定規律選擇I個均分方位，N個頻率建立樣本庫。在樣本庫的建立過程中，可以將方位及頻率步進盡可能最小化，但是樣本采集得越精細，需要耗費的人力以及時間就越多，因此在實際采樣時，選擇了72個均分方位，即對每一個頻點以5°為步進提取原始樣本，然后再對實際采樣數據進行插值，從而獲得每個頻點處360°全方位的樣本數據。

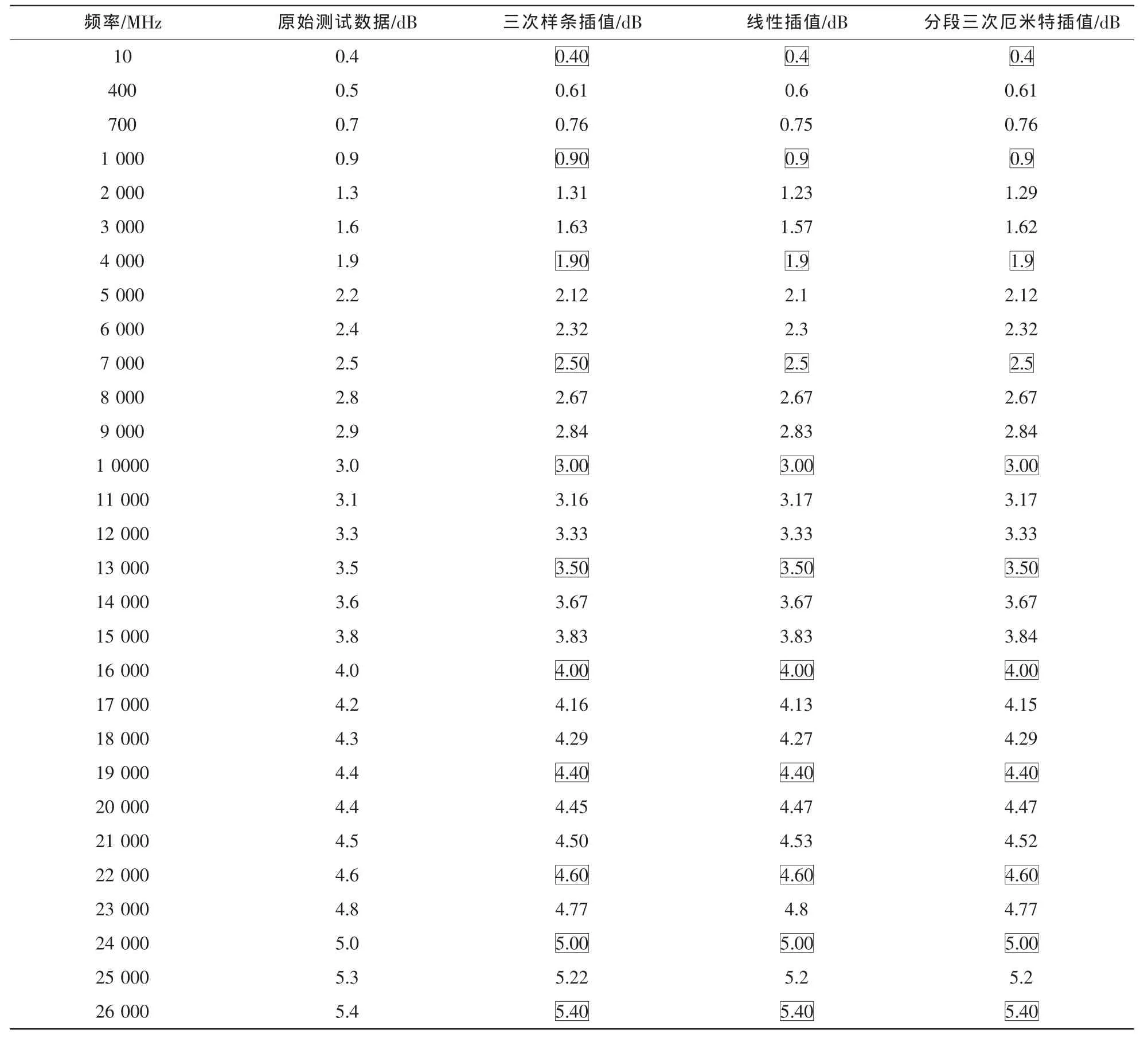
表2 3種不同插值算法的插值結果

圖4 3種插值算法的插值誤差

在本次試驗中，先采集了360°全方位的樣本數據，然后以5°為步進選擇插值點，并將插值得到的結果和原始數據進行對比。試驗中采用的天線為NSMI-CX0230測向天線，接收機為NSMI-JX03雙通道監測測向接收機，該接收機返回的樣本為7維的相位差數據，在此選擇第一維數據來進行3種插值方法的驗證，圖5、圖6分別給出了3種插值算法的插值結果及誤差。

從上述結果中可以看出，3種插值算法得到的結果均可滿足實際需求，但在0°～100°方位內，三次樣條插值要明顯優于另外兩種插值算法，證實了三次樣條插值算法的有效性。

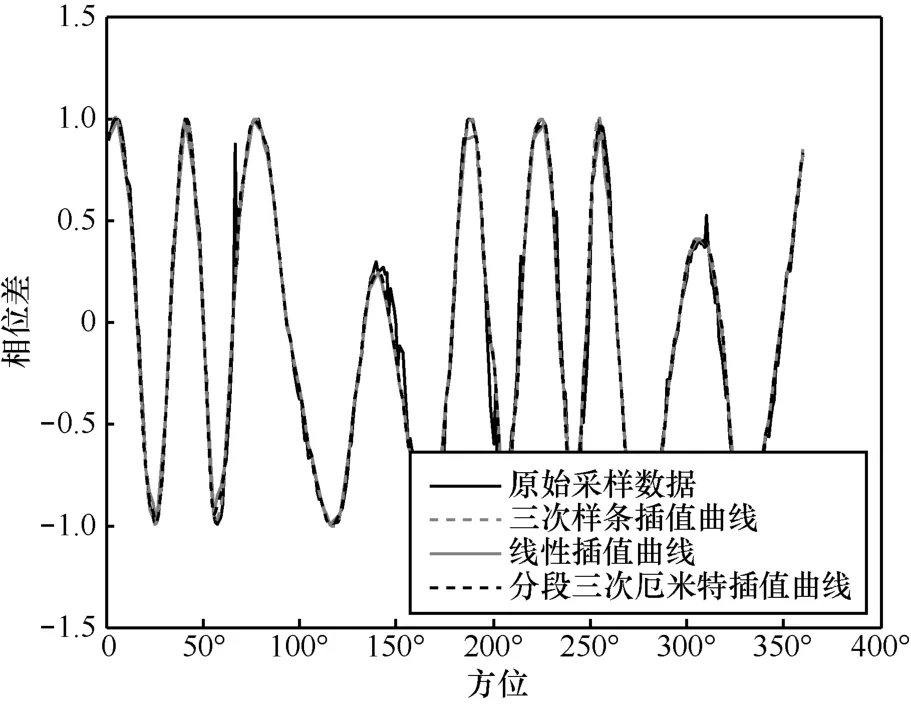
圖5 3種不同插值算法插值結果

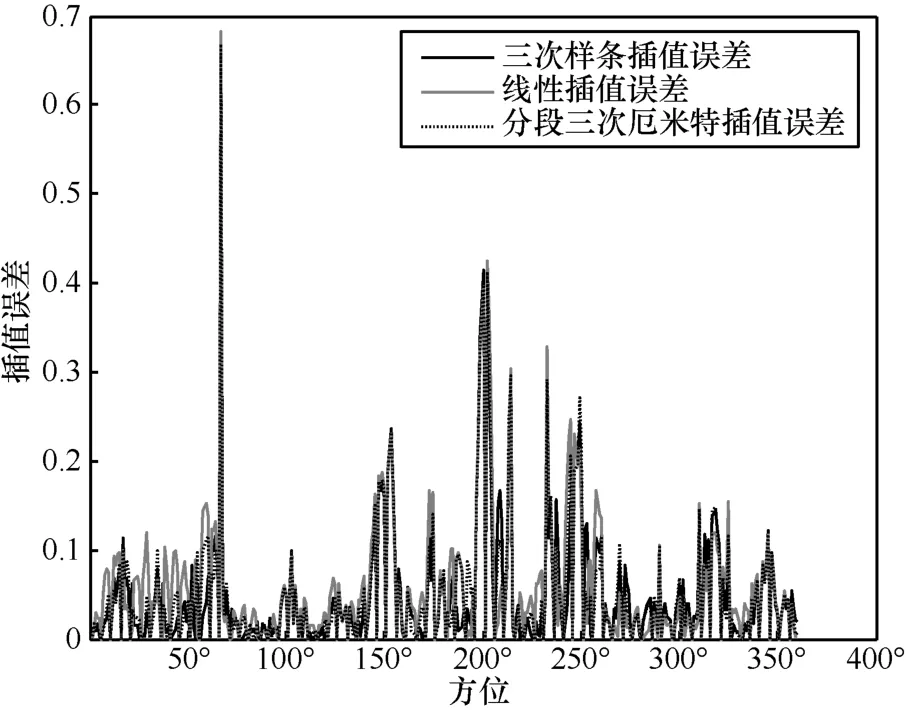
圖6 3種插值算法插值誤差

4 結束語

本文通過對三次樣條插值算法進行研究，將其應用至通信工程實踐中，并通過MATLAB仿真實現了三次樣條插值算法在自由空間損耗計算、饋線插入損耗估計、相關干涉測向3個典型場景下的應用，證實了該插值算法在通信工程應用中的有效性。

[1]孫志忠,吳宏偉,袁慰平,等.計算方法與實習 [M].南京:東南大學出版社,2011. SUN Z Z,WU H W,YUAN W P,et al.An elementary numerical analysls [M].Nanjing:Southeast University Press, 2011.

[2]陳嶺,許曉龍,楊清,等.基于三次樣條插值的無線信號強度衰減模型[J].浙江大學學報(工學版),2011(9):1521-1527. CHEN L,XU X L,YANG Q,et al.Wireless signal strength propagation model base on cubic spline interpolation[J].Journal of Zhejiang University (Engineering Science),2011(9): 1521-1527.

[3]李迪.三次樣條插值在WCDMA移動終端校準中的應用[D].上海:上海交通大學,2009. LI D.Cubic saline interpolation in of WCDMA mobile[D]. Shanghai:Shanghai Jiaotong University,2009.

[4]趙鴻圖,劉云.基于三次樣條插值的小波模極大值去噪算法[J].計算機工程與設計,2014(8):2965-2968. ZHAO H T,LIU Y.Denoising algorithm of wavelet modulus maximum based on cubic spline interpolation [J].Computer Engineering and Design,2014(8):2965-2968.

[5]楊虎山.三次樣條插值在實際問題中的應用和實現[J].忻州師范學院學報,2008,24(2):47-49. YANG H S. The application and realization in a actual problem of cubic spline interpolation[J].Journal of Xinzhou Teachers University,2008,24(2):47-49.

[6]金維剛,劉會金.基于三次樣條插值時域采樣重構的間諧波檢測新算法[J].電網技術,2012,36(7):74-80. JIN W G,LIU H J.A new algorithm for interharmonics measurement based on time domain sampling and reconstruction by cubic spline interpolation [J].Power System Technology, 2012,36(7):74-80.

[7]楊潔,王磊.電磁頻譜管理技術 [M].北京:清華大學出版社, 2015. YANG J,WANG L.Electromagnetic spectrum management technology[M].Beijing:Tsinghua University Press,2015.

Application of cubic spline interpolation in communication engineering

SUOANG Daiji
Office of Yushu Radio Management,Wireless Administration of Qinghai Provincial,Yushu 815000,China

In the communication engineering practice,it often needs to estimate the unknown samples which are missing with the limited samples,then the interpolation operation is needed.Based on the research of cubic spline interpolation,the validity was given in communication engineering applications of the cubic spline interpolation by the experimental results on free space loss calculation,feeder insertion loss estimation,correlative interferometer.

cubic spline interpolation,free-space transmission loss,feeder insertion loss,correlation interferometer direction finding

TN99

A

10.11959/j.issn.1000-0801.2017011

2016-10-01；

2017-01-03

索昂代吉（1980-），女，青海省無線電管理辦公室玉樹管理處玉樹無線電監測站站長，主要研究方向為無線電頻譜利用率、無線電監測技術與應用。