矩形致密油藏直井體積壓裂不穩態壓力半解析方法

王家航, 王樹平, 王曉冬, 董文秀

( 1. 中國地質大學(北京) 能源學院,北京 100083; 2. 中國石化石油勘探開發研究院 海相油氣藏開發重點實驗室,北京 100083)

矩形致密油藏直井體積壓裂不穩態壓力半解析方法

王家航1, 王樹平2, 王曉冬1, 董文秀1

( 1. 中國地質大學(北京) 能源學院,北京 100083; 2. 中國石化石油勘探開發研究院 海相油氣藏開發重點實驗室,北京 100083)

基于點源函數理論和邊界元思想，建立一種可用于致密油藏直井體積壓裂改造非穩態壓力分析的半解析模型。模型考慮改造區與未改造區儲層非均質性的影響，在均質條件下與解析解進行對比與擬合，并應用已建立的模型對改造區與未改造區滲透率差異性、體積壓裂改造程度、改造面積和形態、主裂縫長度及導流能力等參數進行討論。結果表明：隨著改造區內滲透率的增大，壓力損耗減小，受改造區面積的影響，單一提高改造區的地層滲透率對整體壓力影響較小；相同的儲層改造體積情況下，有效裂縫體積較大的開發效果最好。與常規壓裂相比，體積壓裂井的開發效果主要受主裂縫長度的影響而非導流能力。

點源函數； 半解析； 矩形致密油藏； 儲層改造； 滲透率差異性； 導流能力； 裂縫半長

0 引言

近年來，隨著能源市場需求的不斷增大及壓裂技術的長足進步，致密油、致密氣、頁巖氣等非常規油氣藏開采已經成為全球熱點[1-5]。作為典型的非常規資源，致密油藏有良好的流體物性和較差的儲層物性特征。該類油藏的滲透率通常低于1×10-3μm2，孔隙度低于10%[6]，采用常規壓裂改造措施難以滿足工業生產需求，因此需對這類油藏進行大規模的體積壓裂[7-9]。相比于常規壓裂，體積壓裂可在井筒附近形成一定范圍的改造縫網，從而降低滲流阻力，增大泄流面積，提高單井產能[8,10]。體積壓裂改造模型研究的難點主要在于如何正確描述儲層的改造程度、形狀及合理解決改造區與未改造區邊界處的耦合問題。

目前，人們在改造體積的特征及對井的影響方面進行研究。Ketineni S P[11]采用等效橢圓流動模型替代體積改造區域進行模擬，儲層被近似為復合天然裂縫區域，內區為體積改造區域，外區不受改造的影響。他還利用馬修斯修正函數解決橢圓滲流問題，并給出流度比、擴散因數、儲容比、竄流因數等參數的影響。該模型復雜，且不能準確描述主裂縫幾何形態。Zhao Y L等[12]將體積改造區域描述為圓形，從而簡化模型，并給出考慮體積壓裂影響的不穩態壓力特征。Jiang R等[13]對致密儲層的產量遞減進行分析，建立的復合模型的壓裂改造區域被考慮為單孔介質，限制模型的應用范圍。劉雄、姜龍燕等[14-18]基于滲透區域分形和動邊界法，建立致密油藏直井體積壓裂的非穩態產能模型，給出分形系數、啟動壓力梯度、改造半徑等參數對產能的影響。分形模型雖能較好地描述裂縫的空間展布，卻不能對壓力的傳播進行客觀描述及實現對人工裂縫參數的優化。

研究成果主要存在的缺陷：一是體積壓裂的改造區域及地層被考慮為圓形，雖然可對模型進行簡化，但對那些河道沉積形成的條帶狀儲層是不準確的，且由于人工主裂縫狹長，體積改造區域應近似為橢圓或者矩形；二是體積壓裂造成的地層滲透率差異性亦未考慮。筆者將體積改造區域分為內外2個矩形區，內區以經典的Warren-Root雙重介質模型替代，外區為未受改造的普通均質地層。將格林函數與邊界元的思想結合，將內外區離散為多個矩形區塊，每個區塊均質、各向同性。該方法同時具備數值模擬及解析2種方法的優點：一，與數值模擬方法相比，不僅可以處理復雜的滲流問題，且大大減少網格劃分的數量，精度高；二，與解析方法相比，可以有效處理不同屬性區塊的邊界耦合問題，計算速度快，應用范圍不局限于本模型。

1 有限導流垂直裂縫Green函數

在長為xe、寬為ye、高為h的箱形封閉均質地層中有一有限導流垂直裂縫井(見圖1)，在位置(xw、yw)處產生一條板狀橫切垂直裂縫，裂縫的高度等于儲層厚度。若裂縫以總流量qref產出常黏度微可壓縮流體，引發地層產生不穩態Darcy滲流。

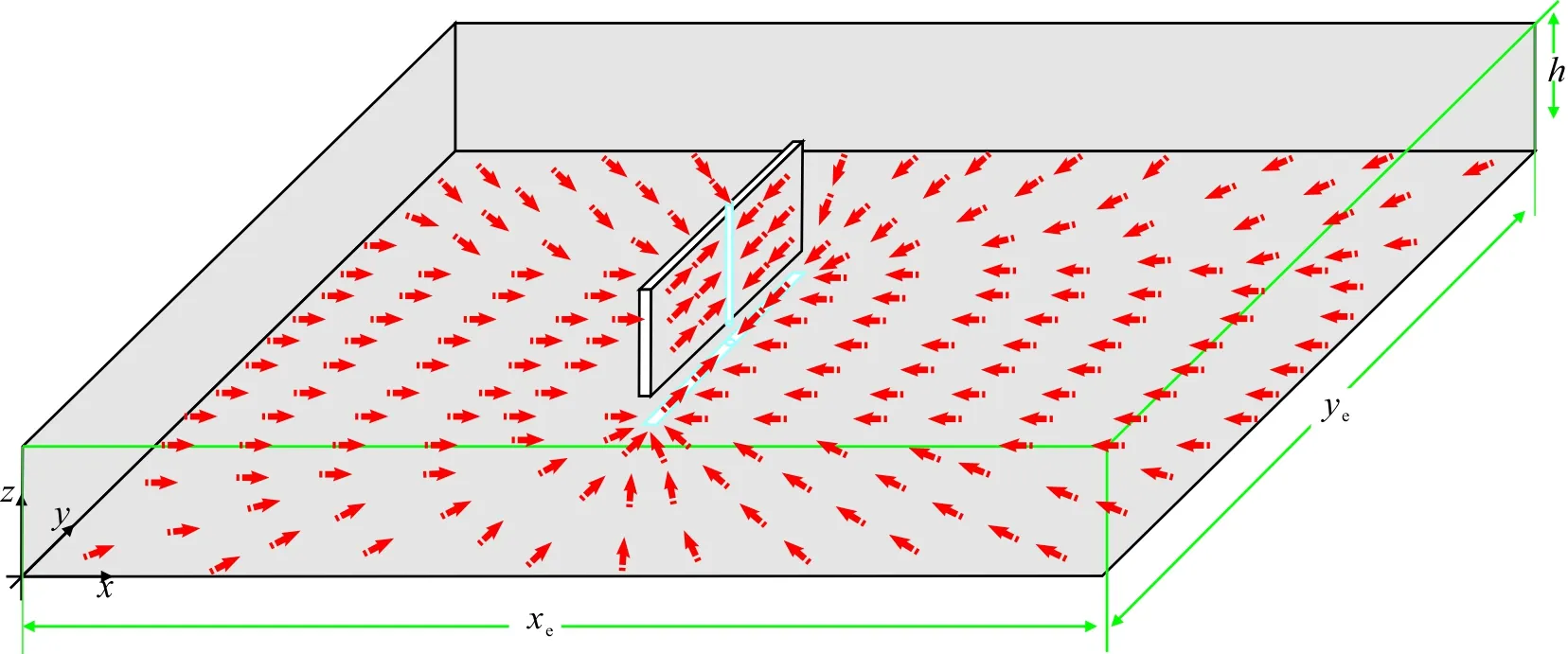
圖1 矩形油藏垂直裂縫示意Fig.1 Sketch for a well with vertical fracture in rectangular reservoir

定義無量綱壓力pD、無量綱時間tD、無量綱導流能力cfiD、無量綱流量qwiD及其他無量綱量為

其中，K1為地層滲透率，可取地層離散后的最小值；Kf為主裂縫滲透率；pi為原始地層壓力；p為儲層任意點處壓力；wf為主裂縫寬度；μ為流體黏度；B為流體體積因數；t為延續時間；φ為儲集層孔隙度；ct為綜合壓縮因數；Lf為特征長度，可取主裂縫離散n段后的最大半長；x、y為平面坐標；xwi為裂縫第i段中心；ywj為裂縫第j段中心；xfi為裂縫第i段半長；qwi為裂縫第i段流量。

對于單一無限導流垂直裂縫情形，通過Green函數求解和Laplace變換，其壓力分布[19]可寫為

(1)

(2)

式(1-2)中：s為Laplace變量，上標“～”為Laplace變換量；“±”為f(a±b)=f(a+b)+f(a-b)。

對于單一有限導流垂直裂縫情形，基于Riley M F[19]的結果，壓力分布可寫為

(3)

(4)

在式(1)中，引入新的參數u將模型擴展到Warren-Root雙重介質模型中代替體積壓裂產生的微裂縫系統[20-21]，即

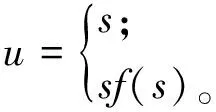
(5)

(6)

式(5-6)中:s為均質油藏;sf(s)為體積壓裂產生的微裂縫系統。

2 物理模型

考慮矩形致密油藏，一口體積壓裂直井定產量生產，體積壓裂造成周圍儲層物性發生改變，地層滲透率變大。天然裂縫、剪切裂縫相互交錯，形成一定的體積改造縫網，流體的滲流方式發生改變。根據儲層物性條件，將整個滲流區分成2個區域(見圖2)：內區為人工主裂縫及縫網改造區，采用Warren-Root模型描述該區域的裂縫展布和滲流情況；外區由于沒有受到體積壓裂的影響，視為普通均質地層。模型的基本假設條件：

(1)整個滲流區域封閉，內區及外區各向同性；

(2)生產井定產，忽略井筒儲集及表皮的影響，流體、巖石微可壓縮；

(3)以裂縫導流為主，滲流遵循Darcy定律，為等溫滲流過程；

(4)忽略重力和毛管力影響。

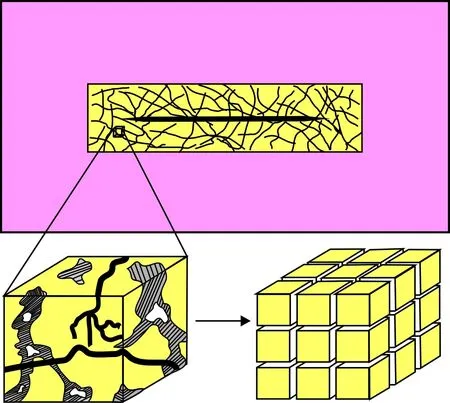
圖2 矩形油藏直井體積壓裂改造示意

3 模型求解

3.1 油藏分區

將內區和外區進一步離散為12個網格(見圖3)，每個網格均質、各向同性。內區與外區的油藏參數不同。整個油藏長為xeD，寬為yeD。

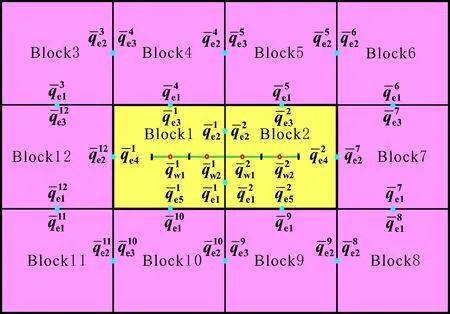
圖3 矩形油藏體積壓裂改造網格模型

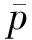
3.2 內外邊界Green函數

假設一個Block中有n+m個(內、外)邊界源，當所有邊界源同時生產，在儲層任意位置MD(xD,yD)處產生的無量綱壓力降，等于單個邊界源獨自工作產生的無量綱壓力降之代數和。由于每個邊界源的總流量是時間函數，根據Duhamel褶積，在Laplace變換域有

(7)

其中，邊界源函數Sα(MD,s)，α=wDi(內邊界源)或α=eDj(外邊界源)，有

(8)

(9)

其中,

(10)

(11)

式(8-11)中：β為各向異性因子；xPi為第i個內邊界源的半長；yPj為第j個外邊界源的半長；Kr為第r個Block的滲透率。

3.3 方程耦合求解

3.3.1 壓力方程

裂縫各段及交界面處各段均有一個壓力方程，共40個。

(1)第k個網格第i段裂縫的壓力為

(12)

共4個方程。

(2)第k個網格第l段的界面壓力為

(13)

(14)

(15)

共36個方程。

3.3.2 交界面處壓力連續條件(基巖系統)

由于Blockk與 Blockk+1界面處壓力相等、流量連續，因此外邊界各段壓力及流量(以Block 1為例)有

(16)

(17)

共18個方程。

3.3.3 井筒壓力條件

忽略裂縫表面的壓力損失，裂縫各段的流壓近似相同，等于井底流壓，即

(18)

(19)

共4個方程。

3.3.4 流量歸一化條件

(20)

AX=b,

(21)

(22)

,

(24)

(25)

(26)

(27)

求解式(21)即可得到井底定產條件下的矩形致密油藏體積壓裂直井的井底壓力。

4 模型驗證

Ozkan E等[20-21]采用點源函數方法，解析求解矩形油藏有限導流垂直裂縫的井底壓力。為了驗證文中模型的準確性，通過式(21)得到相應結果，模型基礎數據見表1，對比結果見圖4。由圖4可知，采用文中模型計算得到的半解析解與前人解析解擬合效果良好。

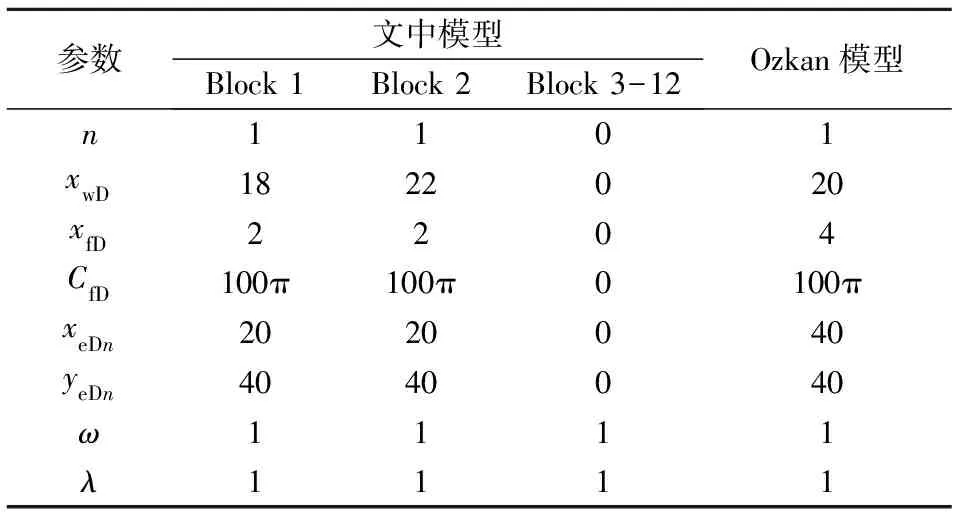
表1 基礎數據

注：n為裂縫段數；xwD為裂縫位置；xfD為裂縫半長；CfD為裂縫導流能力；xeDn為區域長度；yeDn為區域寬度；ω為儲容比；λ為竄流因數

圖4 垂直裂縫井無量綱井底壓力及壓力導數計算對比Fig.4 Calculation comparison for transient pressure and pressure derivative of a well with vertical fracture

5 典型曲線分析

采用Stehfest H[22]數值反演方法對式(21)進行求解，得到井底壓力動態傳播曲線圖，并對其影響參數包括改造區與未改造區的滲透率差異性β、體積改造區面積及形態、改造程度儲容比ω、竄流因數λ、裂縫導流能力CfD、裂縫的半長xfD等進行分析。

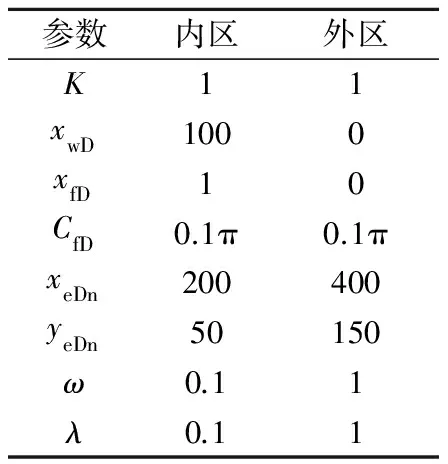
表2 模型基礎數據

注：K為滲透率。

5.1 流動段劃分

模型基礎數據見表2。體積壓裂直井流動階段可劃分為7個階段(見圖5)：(1)人工主裂縫與微裂縫系統的雙線性流。(2)微裂縫系統中的線性流。(3)基質與微裂縫系統之間竄流，基質滲透率極低，壓力降落極緩慢，基質與裂縫之間產生壓力差，引發竄流，壓力導數曲線下凹。(4)改造區內基質的徑向流，壓力導數曲線為0.5水平線。(5)耦合邊界流階段。當儲層體積壓裂改造較好時，內區微裂縫系統滲透率遠大于外區普通地層，內區流體迅速到達井筒，而后者不能提供足夠的流體供應，壓力及壓力導數曲線上揚，類似弱補給或者封閉邊界特征。(6)未改造區地層徑向流。(7)封閉邊界擬穩態流，壓力及壓力導數曲線呈45°上揚。

5.2 影響因素分析

5.2.1 滲透率差異性

“當務之急是加強規章制度建設，使‘糧食銀行’在統一制度和規則下運行。”祝躍華認為，應從國家層面總結各地經驗，針對“糧食銀行”存在的風險漏洞，建立健全規章制度，使其有章可循、規范運作、健康發展。多位受訪者認為，“糧食銀行”經營業務涉及千家萬戶，遭遇糧食市場低迷行情，運行暴露出的多重風險值得關注，亟待出臺政策引導和規范。

滲透率差異性對井底壓力動態傳播的影響分別見圖6-8。由圖6-7可知，隨著儲層整體滲透率的增大，無量綱壓力下降，相同產量情況下的壓力損耗減小，晚期邊界流發生的時間變早。儲層改造區內滲透率差異性的影響類似于整體滲透率，但相對較小。由圖8可知，隨著內、外區滲透率差異性的增大，外區地層徑向流動段的持續時間逐漸變短直至消失。這是由于內區微裂縫系統滲透率遠大于外區普通地層的，后者不能提供足夠的流體供應，類似弱補給或者封閉邊界特征。因此，在體積壓裂過程中，應盡可能加大壓裂規模，提高儲層整體的滲透率。

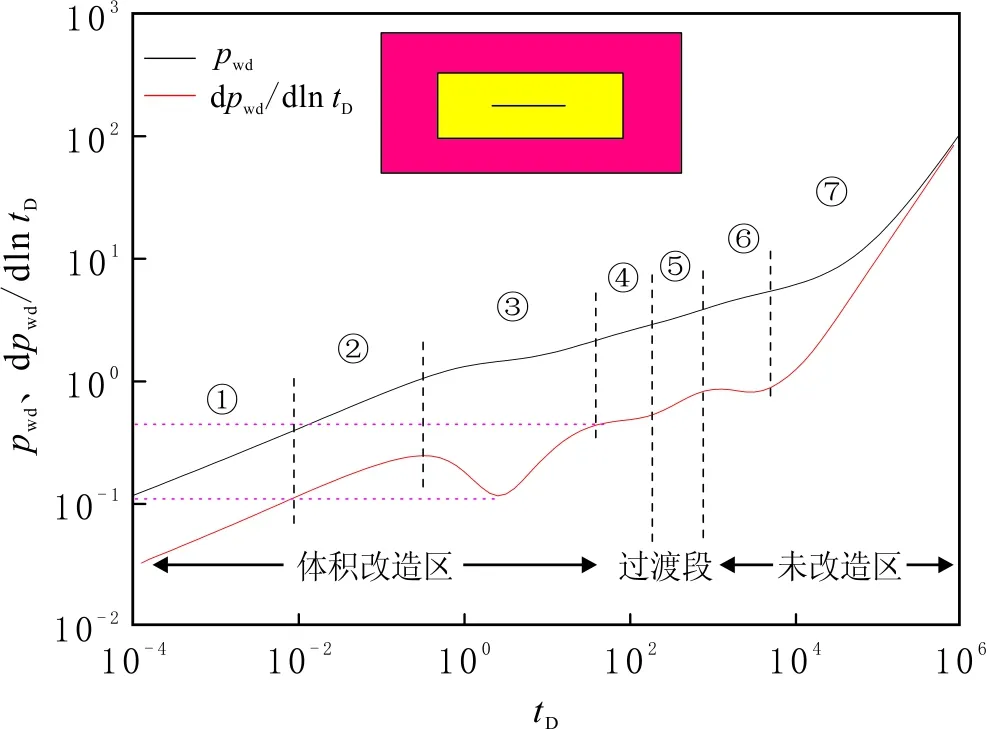
圖5 體積壓裂直井流動階段Fig.5 Flow stages of volume fractured vertical wells

5.2.2 體積壓裂改造程度

儲層改造程度對井底壓力動態傳播的影響見圖9-10。由圖9-10可知，儲容比和竄流因數主要影響改造區內基質與微裂縫系統竄流發生的程度和時間。儲容比描述裂縫系統和基質系統彈性儲容能力的相對大小。儲容比越小，竄流現象越明顯，無量綱壓力導數曲線下凹越深；竄流因數對基質—裂縫竄流階段有影響，反映基質中流體向裂縫竄流的能力。竄流因數越小，基質向裂縫流動引起竄流的時間越晚。

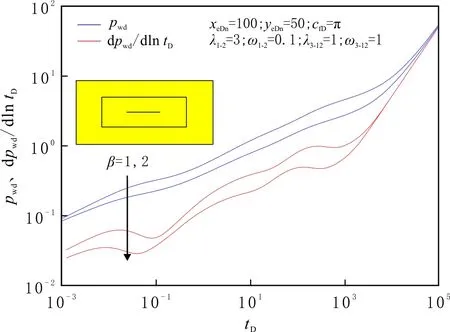
圖6 受儲層整體滲透率影響的井底壓力及壓力導數曲線Fig.6 Effect of reservoir permeability for the pressure and pressure derivative curves

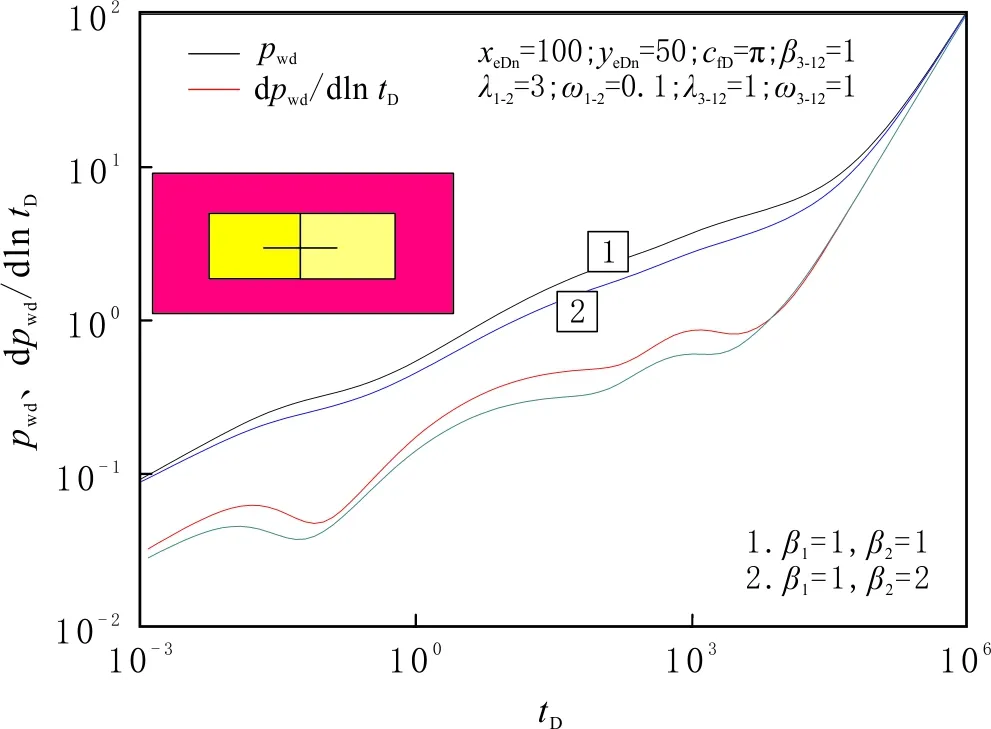
圖7 受內區滲透率非均質性影響的井底壓力及壓力導數曲線Fig.7 Effect of permeability heterogeneity in the inner region for pressure and pressure derivative curves

5.2.3 體積壓裂改造面積及形態

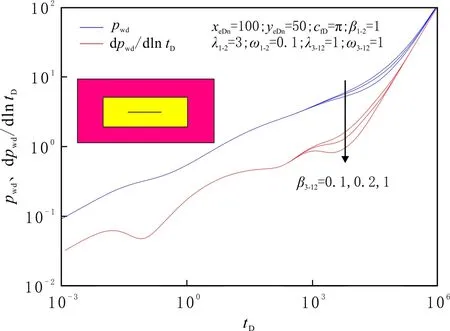
圖8 受外區滲透率影響的井底壓力及壓力導數曲線Fig.8 Effect of outer region permeability for pressure and pressure derivative curves

儲層壓裂改造面積及縫網改造形態對井底壓力傳播的影響見圖11-12。由圖11可知：隨著儲層壓裂改造面積的增大，壓力及壓力導數逐漸變小。改造面積S越大，內區徑向流持續的時間越長，壓力傳播到改造區外邊界的時間越晚，外區地層徑向流發生的時間也越晚。隨著改造面積的增大，無量綱壓力降低的趨勢逐漸趨于平緩。這是由于單井的控制儲量有限，無限制增大儲層的改造面積意義不大，且增加施工的難度及費用。因此，在體積壓裂設計過程中，應做好改造面積的優化選擇。

由圖12可知，在儲層改造體積相同的情況下，正方形縫網的壓力損耗低于矩形縫網的，且隨著矩形縫網長寬比的逐漸增大，壓力損耗增加。這是因為人工主裂縫的導流能力較大，早期的滲流主要發生在主裂縫及其附近的改造縫網，不受縫網形態的影響；隨著開采時間的增加，壓力波及范圍逐漸增大直至縫網邊緣，有效裂縫體積較大的儲層垂向動用程度較好[23]。因此，在體積壓裂設計中，不僅要選擇最優化的縫網改造面積，縫網改造形態也是必須考慮的因素。

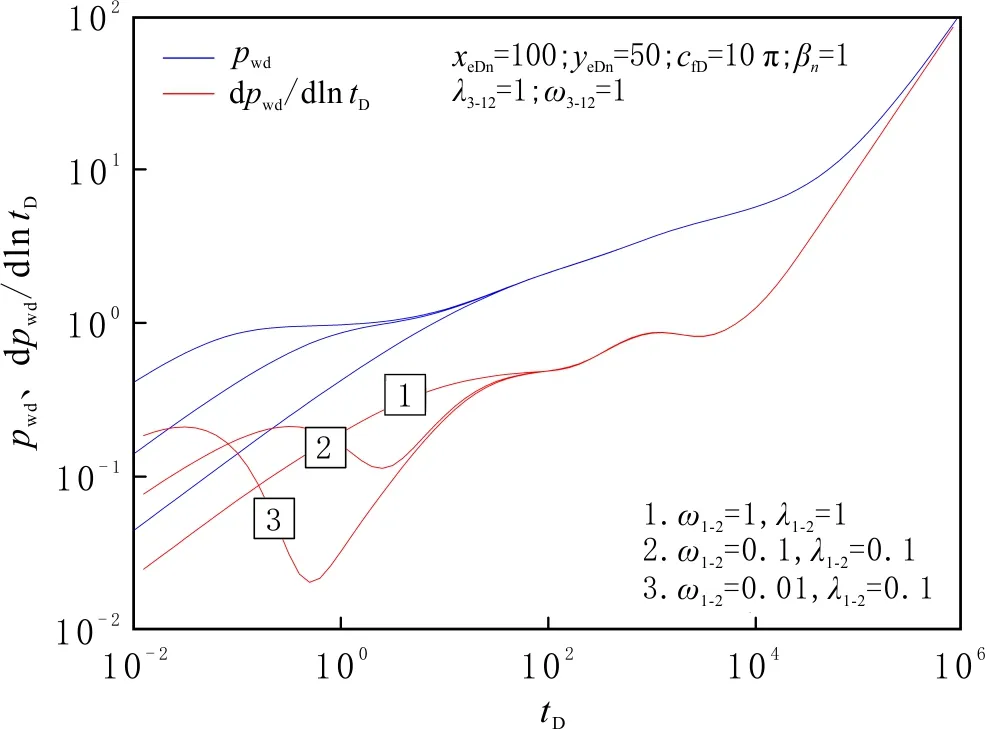
圖9 不同儲容比條件下的井底壓力及壓力導數曲線Fig.9 Pressure and pressure derivative curves for different storability ratios

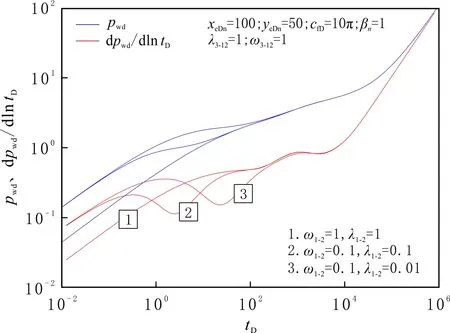
圖10 不同竄流因數條件下的井底壓力及壓力導數曲線Fig.10 Pressure and pressure derivative curves for different inter-porosity flow coefficient ratios

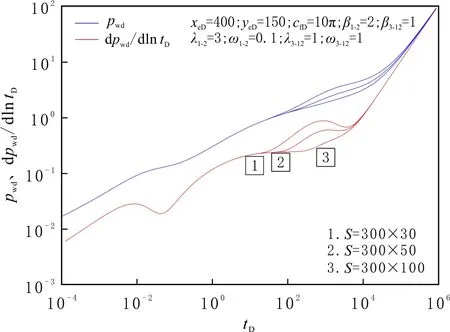
圖11 不同儲層改造面積條件下的井底壓力及壓力導數曲線Fig.11 Pressure and pressure derivative curves for different reservoir reconstruction areas

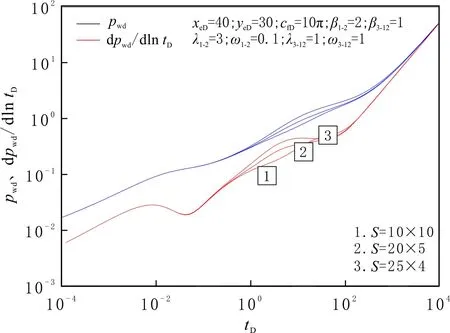
圖12 不同縫網改造形態條件下的井底壓力及壓力導數曲線Fig.12 Pressure and pressure derivative curves for different shapes of reservoir reconstruction region

5.2.4 裂縫導流能力cfD

對于常規壓裂，單一裂縫的導流能力是評價裂縫質量的重要指標，對油井生產動態指標影響很大。同樣，體積壓裂產生的人工主裂縫導流能力也直接影響最終的開發效果。不同裂縫導流能力條件下的井底壓力及壓力導數曲線見圖13。由圖13可知，隨著導流能力的增大，雙線性流的持續時間逐漸增大，線性流的持續時間減少，壓力損耗降低。當無量綱導流能力大于300時，壓力導數曲線不再發生變化，可以認為是無限導流裂縫。導流能力僅對早期的流動有影響，因此無限制的增加人工主裂縫的導流能力對井產能的提高有限。

5.2.5 裂縫半長xfD

不同裂縫長度條件下的井底壓力及壓力導數曲線見圖14。由圖14可知，裂縫的半長主要對早期雙線性流、線性流及內區基質徑向流有影響。裂縫的半長越大，即裂縫的穿透比越大，早、中期的壓力及壓力導數越小，壓力損耗越低。對于致密油藏的體積壓裂直井，與常規油藏相反，裂縫的半長較導流能力的影響更大。這是因為隨著裂縫長度的增加，更多由體積壓裂產生的微裂縫及儲層被勾通，流體的有效泄流面積增大，產量增大。因此，在改造體積不變的情況下，應盡可能增大裂縫的穿透比。

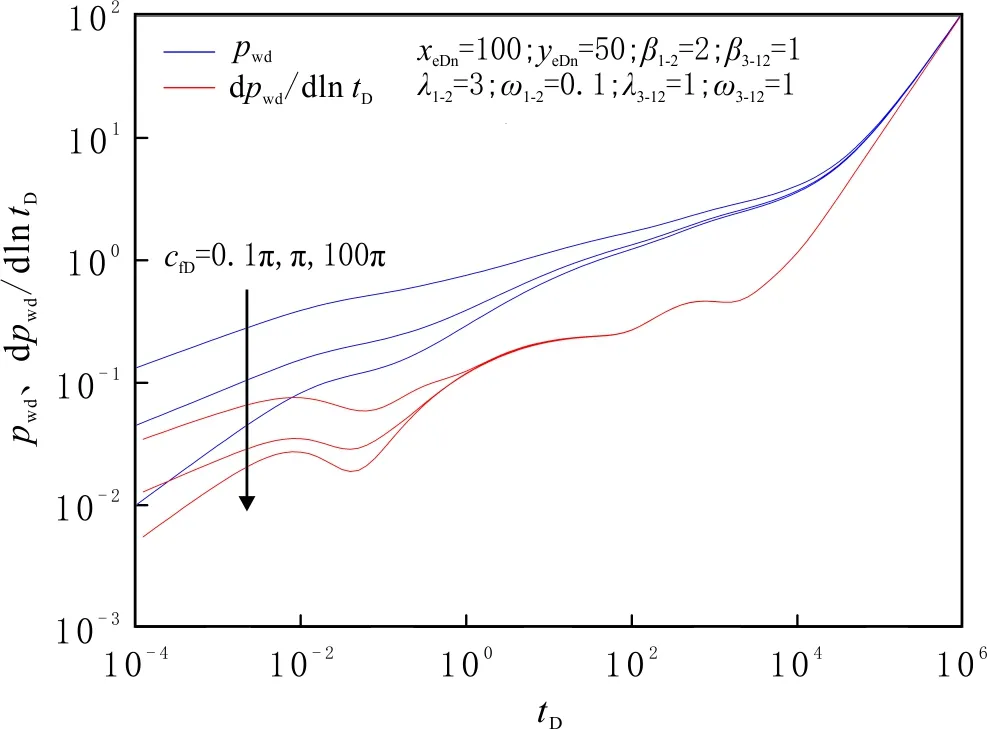
圖13 不同裂縫導流能力條件下的井底壓力及壓力導數曲線Fig.13 Pressure and pressure derivate curves for different fracture conductivities

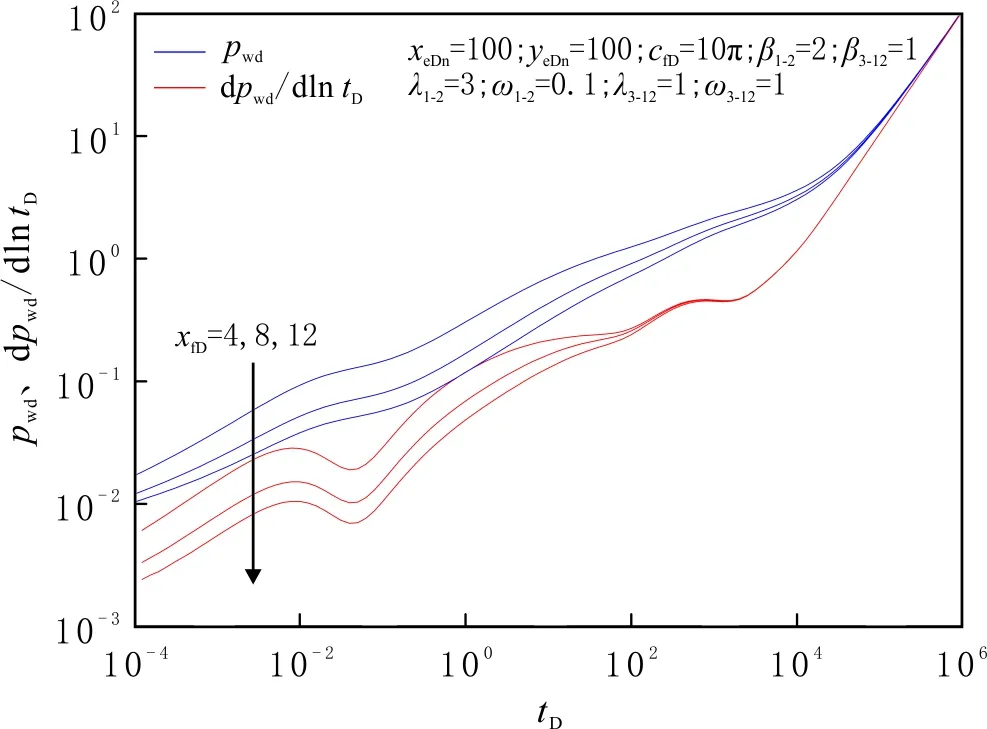
圖14 不同裂縫長度條件下的井底壓力及壓力導數曲線Fig.14 Pressure and pressure derivate curves for different facture lengths

6 結論

(1)矩形致密油藏體積壓裂直井的流動階段可劃分為7個階段，即人工主裂縫與微裂縫系統的雙線性流；微裂縫系統中的線性流；基質與微裂縫系統之間竄流；改造區內基質的徑向流；耦合邊界流階段與未改造區地層徑向流和封閉邊界擬穩態流。

(2)體積壓裂造成縫網改造區與未改造區的滲透率差異性，隨著縫網改造區內滲透率的增大，相同產量下的壓力損耗減小，但單一提高改造區的地層滲透率對整體的壓力影響有限。在體積壓裂過程中，應盡可能提高儲層整體的滲透率。

(3)儲容比和竄流因數分別影響竄流發生的程度和時間。儲容比越小，竄流現象越明顯；竄流因數越小，竄流發生的時間也越晚。儲容比僅對早期的壓力有影響，儲容比越大，壓力損耗越小；竄流因數對竄流發生段的壓力有影響，竄流因數越大，對應生產期的產量也越高。

(4)儲層的改造體積并不是越大越好，在保證壓裂措施工藝承受的范圍內，壓力的損耗最低是進行儲層改造體積設計的首要目標。在相同的儲層改造體積情況下，正方形的縫網較矩形的動用程度大，即有效裂縫體積較大的開發效果最好。

(5)與常規壓裂相比，體積壓裂井的開發效果主要受縫網長度即主裂縫長度的影響。在致密油藏直井的體積壓裂設計中，要達到理想的壓裂效果，在保證較大導流能力的同時，應盡可能增大人工主裂縫的長度。

[1] Brohi I, Pooladi-Darvish M, Aguilera R. Modeling fractured horizontal wells as dual porosity composite reservoirs-application to tight gas, shale gas and tight oil cases [C]. SPE 144057,2011.

[2] Zhou W, Gupta S, Banerjee R, et al. Production forecasting and analysis for unconventional resources [C]. IPTC 17176, 2013.

[3] Chengzao J, Zheng M, Zhang Y. Unconventional hydrocarbon resources in China and the prospect of exploration and development [J]. Petroleum Exploration and Development, 2012,39(2):139-146.

[4] Nelson P H. Pore-throat sizes in sandstones, tight sandstones and shales [J]. AAPG bulletin, 2009,93(3):329-340.

[5] Lei X, Yongmin S, Changsheng X, et al. Influences of feldspars on the storage and permeability conditions in tight oil reservoirs: A case study of chang-6 oil layer group, Ordos basin [J]. Petroleum Exploration and Development, 2013,40(4):481-487.

[6] Zou C, Zhu R, Wu S, et al. Types, characteristic, genesis and prospects of conventional and unconventional hydrocarbon accumulations: Taking tight oil and tight gas in China as an instance [J]. Acta Petrolei Sinica, 2012,33(2):173-187.

[7] Agboada D K, Ahmadi M. Production decline and numerical simulation model analysis of the eagle ford shale play [C]. SPE Western Regional & AAPG Pacific Section Meeting 2013 Joint Technical Conference. Society of Petroleum Engineers, 2013.

[8] Wang H, Liao X, Lu N, et al. A study on development effect of horizontal well with SRV in unconventional tight oil reservoir [J]. Journal of the Energy Institute, 2014, 87(2):114-120.

[9] Mayerhofer M J, Lolon E P, Youngblood J E, et al. Integration of microseismic-fractured-mapping results with numerical fracture network production modeling in the Barnett shale [C]. SPE Annual Technical Conference and Exhibition. Society of Petroleum Engineers, 2006.

[10] Mayerhofer M J, Lolon E, Warpinski N R, et al. What is stimulated reservoir volume [J]. SPE Production & Operations, 2010,25(1):89-98.

[11] Ketineni S P. Analysis of production decline characteristic of a multi-stage hydraulically fractured horizontal well in a naturally fractured reservoir [D]. Pennsylvania: The Pennsylvania State University, 2012.

[12] Zhao Y L, Zhang L H, Luo J X, et al. Performance of fractured horizontal well with stimulated reservoir volume in unconventional gas reservoir [J]. Journal of Hydrology, 2014,512(10):447-456.

[13] Jiang R, Xu J, Sun Z, et al. Rate transient analysis for multistage fractured horizontal well in tight oil reservoir considering stimulated reservoir volume [C]. Mathematical Problems in Engineering, 2014.

[14] 劉雄,田昌炳,姜龍燕,等.致密油藏直井體積壓裂穩態產能評價模型[J].東北石油大學學報,2014,38(1):91-96. Liu Xiong, Tian Changbing, Jiang Longyan, et al. Steady deliverability evaluation model of fracture network reconstruction vertical well in tight oil reservoir [J]. Journal of Northeast Petroleum University, 2014,38(1):91-96.

[15] 姜龍燕,荀小全,王楠,等.致密油藏直井體積壓裂非穩態產能評價模型[J].斷塊油氣田,2015,22(1):82-86. Jiang Longyan, Xun Xiaoquan, Wang Nan, et al. No-steady productivity evaluation model of volume fracturing for vertical well in tight oil reservoir [J]. Fault-Block Oil& Gas Field, 2015,22(1):82-86.

[16] 劉雄.致密油儲層體積改造產能評價方法研究[D].北京:中國地質大學(北京),2013. Liu Xiong. The research of deliverability evaluated for volume reconstruction in tight oil reservoir [D]. Beijing: China University of Geosciences (Beijing), 2013.

[17] 劉雄,田昌炳,萬英杰,等.裂縫性致密油藏直井體積改造產能評價模型[J].現代地質,2015,29(1):131-137. Liu Xiong, Tian Changbing, Wan Yingjie, et al. Deliverability evaluation model of fracture network reconstruction vertical well in fractured tight oil reservoir [J]. Geoscience, 2015,29(1):131-137.

[18] 劉雄,田昌炳,紀淑紅,等.致密油藏體積壓裂直井非穩態壓力分析[J].特種油氣藏,2015,22(5):82-86. Liu Xiong, Tian Changbing, Ji Shuhong, et al. Transient pressure analysis of volume fracturing in vertical wells in tight reservoirs [J]. Special Oil and Gas Reservoirs, 2015,22(5):95-99.

[19] Riley M F. Analytical solutions for elliptical finite-conductivity fractures [C]. SPE 22656 Presented at the 66th Annual Technical Conference and Exhibition of the Society of Petroleum Engineering held in Dallas, TX, 1991.

[20] Ozkan E, Raghavan R. New solutions for well-test-analysis problems: Part 1-anaytical considerations [C]. SPE 18615-PA, 1991.

[21] Ozkan E, Raghavan R. New solutions for well-test-analysis problems: Part 2-computional considerations and applications [C]. SPE 18616-PA, 1991.

[22] Stehfest H. Numerical inversion of Laplace transforms [J]. Communications of the ACM, 1970,13(1):47-49.

[23] 王文東,蘇玉亮,穆立俊,等.致密油藏直井體積壓裂儲層改造體積的影響因素[J].中國石油大學學報:自然科學版,2013,37(3):93-97. Wang Wendong, Sun Yuliang, Mu Lijun, et al. Influencing factors of stimulated reservoir volume of vertical wells in tight oil reservoirs [J]. Journal of China University of Petroleum: Science & Technology Edition, 2013,37(3):93-97.

2016-12-28；編輯：關開澄

國家自然科學基金項目(51674227)

王家航(1988-)，男，博士研究生，主要從事油氣田開發方面的研究。

TE348

A

2095-4107(2017)02-0103-11

DOI 10.3969/j.issn.2095-4107.2017.02.011