基于6σ穩健性的軋制差厚板車門優化設計

朱茂桃 朱彩帆 郭佳歡 錢 洋

1.江蘇大學汽車與交通工程學院，鎮江，2120132.博世汽車零部件公司，蘇州，215100

基于6σ穩健性的軋制差厚板車門優化設計

朱茂桃1朱彩帆1郭佳歡1錢 洋2

1.江蘇大學汽車與交通工程學院，鎮江，2120132.博世汽車零部件公司，蘇州，215100

目前，對車門結構優化的研究多數沒有考慮車門不確定性因素的影響。為了提高結構優化后車門性能的穩健性，將軋制差厚板應用于車門，同時考慮板料厚度和材料參數的波動對各約束響應穩健性的影響。結合拉丁超立方試驗設計和徑向基函數模型，采用蒙特卡羅模擬和改進型非支配遺傳算法相結合的雙循環優化策略，提出一種基于6σ穩健性的軋制差厚板車門多目標優化設計方法。研究結果表明，該方法在獲得最優妥協解的同時，能提高設計變量的可靠性和目標函數的穩健性。

車門；穩健性；軋制差厚板；蒙特卡羅模擬；輕量化

0 引言

車門是整車的重要零部件之一，應滿足強度、剛度和模態性能的要求。減小車門質量是節約能源、提高燃油經濟性、減少環境污染的基本途徑之一[1]，因此對車門輕量化研究是非常必要的。在車門設計和改進時如何兼顧輕量化和穩健性這兩個要求，已成為汽車行業研究的熱點問題。

實際生產過程中，制造工藝、工人操作及環境中的不確定性因素會引起板料厚度在名義設計值附近波動，這將導致車門結構性能的波動，使得確定性優化結果超出約束邊界條件而缺乏可靠性。此外，材料性能參數受隨機噪聲因素的干擾，也會使得最優設計點不可靠，所以在輕量化應用工程中應盡量減小最優設計點對干擾的敏感性[2]。

許多學者對穩健性優化理論方法進行了研究。GUNAWAN等[3-4]針對單目標穩健優化，采用非梯度參數靈敏度分析方法，有效地提高了最優設計點的穩健性，并在此基礎上提出“靈敏度域”的概念，并將其應用于多目標、多約束穩健優化問題，但該方法未能有效地解決此類問題。YOUN等[5]提出了以提高最優設計點的可靠性為優化目標的設計方法，使設計響應均值遠離邊界條件，但此方法在滿足可靠性條件的同時未能兼顧目標的穩健性。李玉強等[6]采用6σ穩健性優化設計方法，將6σ質量管理、可靠性優化設計與基于容差模型的穩健性優化設計相結合，使響應均值遠離邊界條件，能同時提高設計的可靠性和穩健性。

本文根據某車門靜剛度和模態分析的結果，對其剛度和模態性能進行優化。將6σ穩健性優化和多目標優化設計相結合，充分考慮門板厚度和材料性質等不確定因素，結合蒙特卡羅模擬(Monte Carlo simulation，MCS)技術和改進型非支配遺傳算法(NSGAⅡ)，構造基于6σ穩健性的軋制差厚板(tailor rolled blank，TRB)車門輕量化設計方法。

1 車門有限元模型的建立與驗證

車門由厚度小于2 mm的金屬薄板沖壓焊接而成，因此車門的有限元模型主要用面網格進行離散化[7]，即對曲面率較小的平坦區域選用四邊形單元劃分，對曲率較大的過渡區域選用三角形單元劃分，并控制三角形單元的網格數量小于整個車門有限元模型網格數量的10%[8]。焊點采用rigid剛性單元模擬。車門的材料為08AL，此材料的彈性模量為207 GPa，泊松比為0.3，密度為7800 kg/m3。利用Hypermesh建立的車門有限元模型如圖1所示。

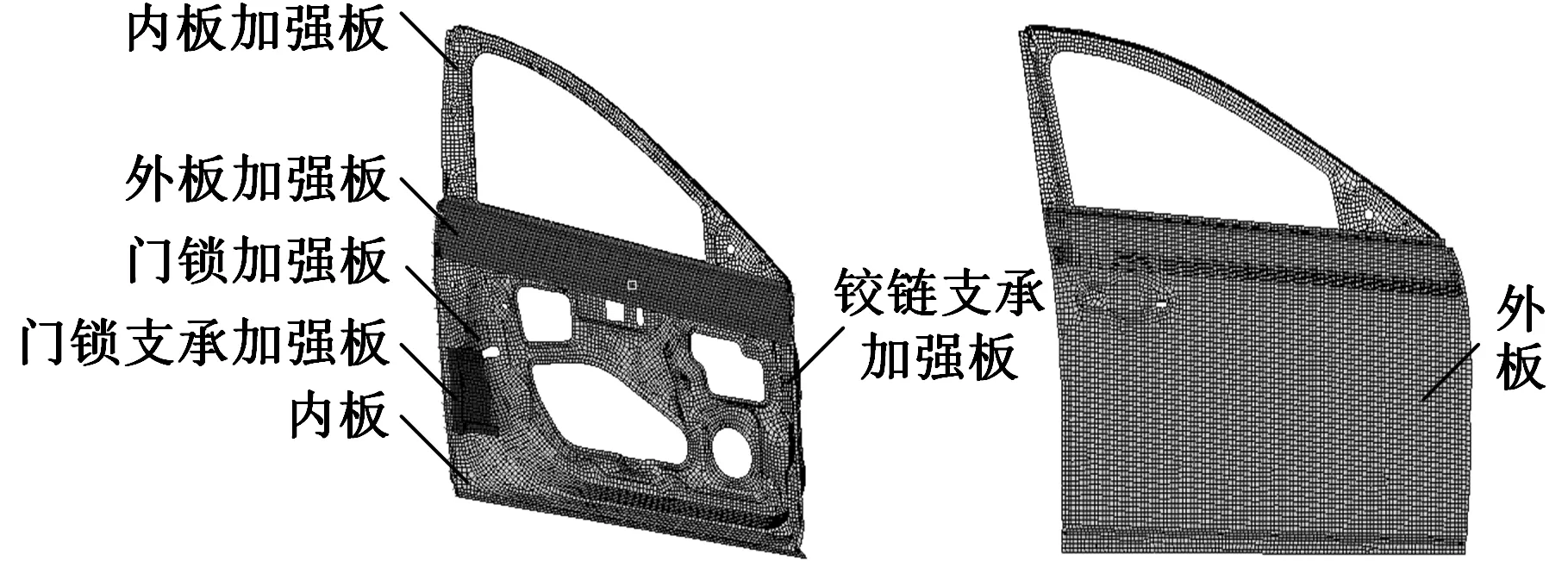
圖1 車門有限元模型Fig.1 Finite element model of car door

利用Optistruct對車門剛度和模態進行有限元分析，發現車門局部區域的剛度不足，需進行結構優化。后文將軋制差厚板用于車門結構優化時，將剛度不足區單獨進行分塊處理。車門一階模態頻率為34.83 Hz，與一般情況下轎車車身一階固有頻率相近，存在共振的可能性，故需進行剛度和模態性能的優化，即在滿足車門剛度和模態性能的前提下，以車門質量最小為目標進行優化設計。

車門的有限元模型與車門實體之間存在差異，故在對車門進行結構優化前，需對車門的有限元模型進行驗證，即用模態試驗驗證車門有限元模型的正確性，為后續研究奠定基礎。試驗時，車門采用充氣內胎支撐，采用等間距的密集布點法布置107個測試點。采用力錘錘擊法模擬激勵信號，逐步測取107個測試點的響應信號。激勵信號與響應信號經過放大器輸入動態信號分析儀，采用FFT處理激勵信號和各測點響應信號，得到120 Hz以內的模態響應值，最后在STAR分析軟件中進行曲線擬合，通過模態參數識別，得到車門模態參數，車門模態試驗測試系統如圖2所示。將試驗和理論模態結果進行比較，對比結果如表1所示。

由表1可知，前6階模態振型中，車門試驗模態沒有第1階模態，這是因為車門模態分析中所建立的有限元模型有26 300個節點，而車門試驗模態中僅有107個測試點，有限元模型節點數遠遠大于試驗模態測點數。計算值與試驗值之間的相對誤差最大為8.36%，滿足小于10%的要求。綜上可知，車門理論模態與試驗模態頻率相近，因此有限元模型有效反映了車門實體屬性，能夠用于后續優化設計的研究。

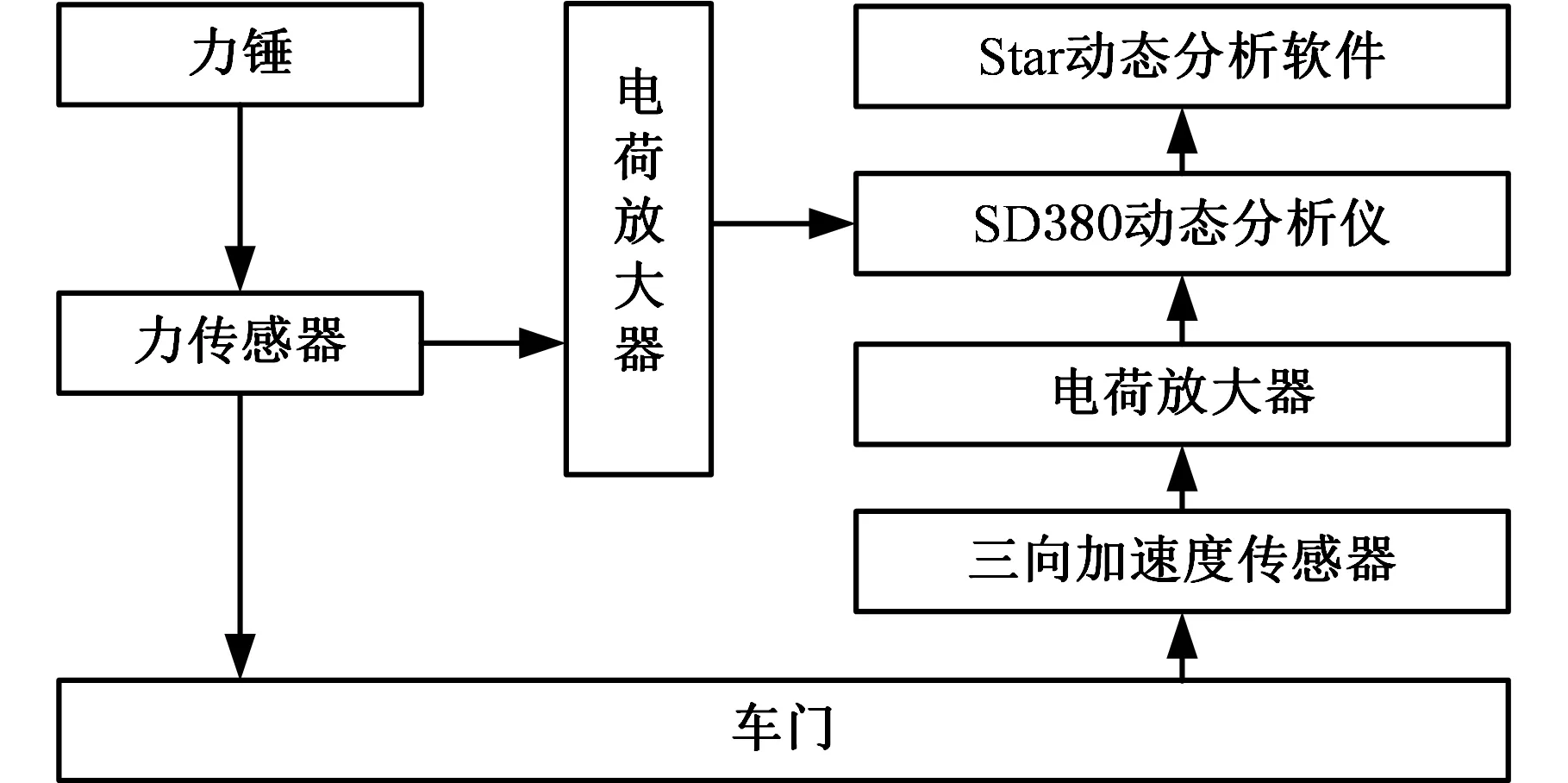
圖2 車門模態試驗測試系統示意圖Fig.2 Test system diagram of car door modal test

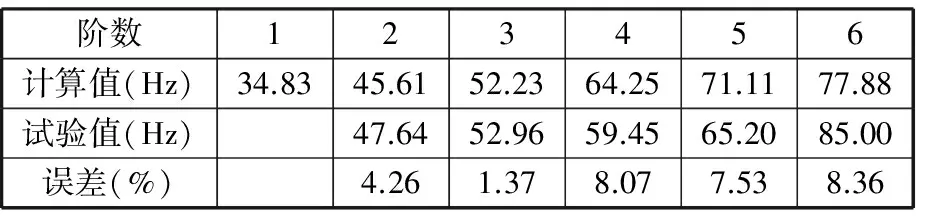
階數123456計算值(Hz)34．8345．6152．2364．2571．1177．88試驗值(Hz)47．6452．9659．4565．2085．00誤差(%)4．261．378．077．538．36

2 車門確定性優化流程

2.1 車門內外板分塊處理

對車門進行靜剛度和模態分析，通過分析車門結構在各個工況下的應力云圖和變形云圖可知，車門內板主要承載區為車門鉸鏈連接處、窗框邊緣和內板腰帶處。車門外板主要承載區為窗框下邊緣和外板下端。據此將車門內板分成4個區域，將車門外板分成3個區域，如圖3所示。用軋制差厚板代替原有的等厚度板和加強板，為后續優化做準備。圖3中，區域4、區域6為厚度連續線性變化的過渡區域，在Hyperstudy中通過等式T4=0.5(T1+T2)和T6=0.5(T5+T7)將設計變量關聯起來(Ti為區域i的板材厚度)，并通過Hypermorph中的兩個形狀變量S1、S2來實現區域4和區域6的位置變化，S1表示內板區域3右邊緣的位置沿Z軸方向移動的范圍，S2代表車門內板過渡區域4沿Y軸方向移動的范圍。

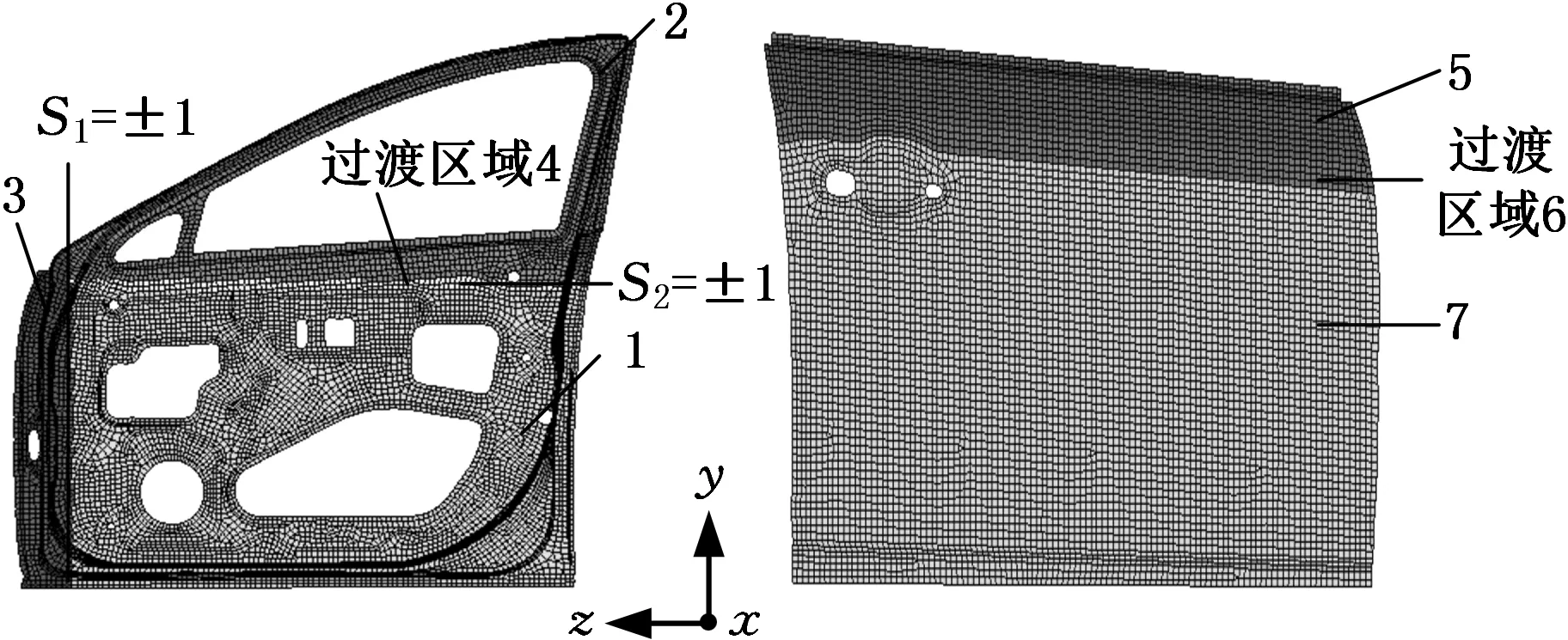
圖3 車門分塊示意圖Fig.3 TRB blocks diagram of car door

2.2 基于試驗設計的徑向基函數模型的構建

合理的試驗設計能提高代理模型的精確度，從而提高優化設計結果的準確度。試驗設計方法主要有兩種：基于邊界填充與基于空間填充。基于空間填充的試驗設計方法不僅可以盡可能多地表達空間特性，而且可以避免邊界的隨機誤差。常見的基于空間填充的試驗設計方法有均勻設計和拉丁超立方設計。拉丁超立方設計方法不僅可以保證設計變量在投影上的均勻性，而且可以保證設計變量在空間上的均勻性，故本文采用拉丁超立方試驗設計方法，按表2中設計變量的范圍，設置成11個因素和150個水平的試驗設計，通過150次不斷調用Hypermesh對每一個試驗點進行有限元分析。車門靜剛度是指車門在使用過程中承受各種載荷情況、抵抗變形的能力，是車門開發設計中的重要參數，一般包括下沉剛度、車窗側向剛度和腰帶擠壓剛度。本文選取下沉工況下車門門鎖處10 217節點的Y向位移d1、窗框側向工況下車門123 562節點的X向位移d2、車門腰帶擠壓工況下車門124 920節點的X向位移d3以及車門一階彎曲頻率f、車門總質量m為響應變量，對車門下沉剛度、窗框側向剛度、腰帶擠壓剛度和1階彎曲頻率f提出評價標準，如表3所示。

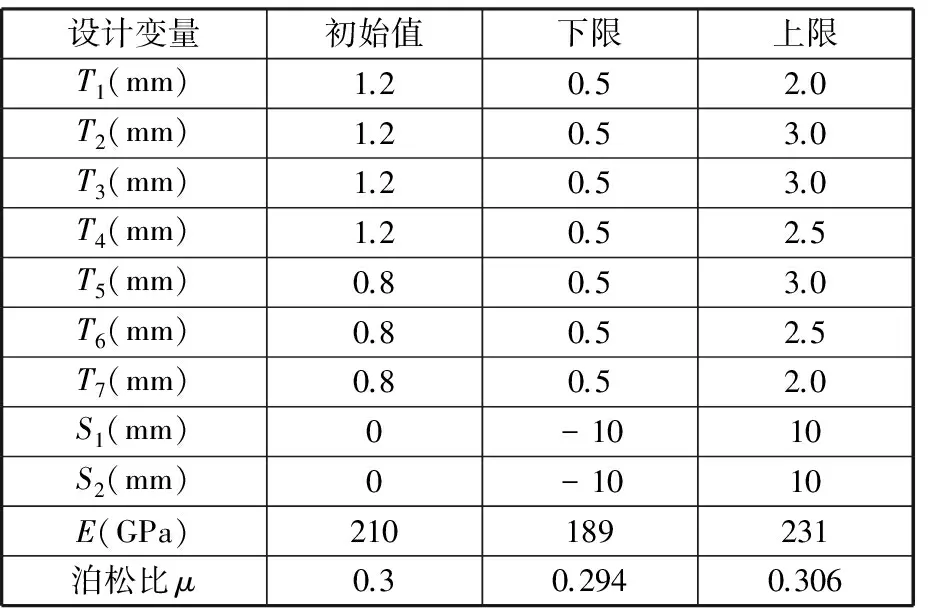
表2 設計變量初始值及取值范圍

表3 評價標準

不同的代理模型適用于不同的問題，總結前人研究成果發現：徑向基函數(RBF) 模型適用性較強；多項式響應面模型(response surface method, RSM)在解決變量較少、低階非線性問題方面具有上佳表現[7]。本文研究的車門多學科穩健性優化設計屬于多變量、非線性問題，因此選用RBF模型。

RBF模型以徑向函數為基函數，通過線性疊加構造出來的模型，將多維問題轉化為以徑向函數為自變量的一維問題，能很好地兼顧計算效率和精度[9-10]。用RBF模型代替車門有限元模型進行優化時需對代理模型精度進行評價，評價指標包括決定系數R2和均方差EMS，分別為

(1)

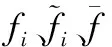
R2體現了代理模型對樣本點的擬合情況，其值越接近1，精度越高；EMS越小表示代理模型精度越高。本文選取10個樣本點，進行交叉驗證，5個響應量的RBF模型的決定系數均大于0.9，均方差均小于0.1 (表4)，說明建立的RBF模型精度達到了較高水平，可用于下一步的優化設計。

表4 RBF模型交叉驗證評價參數

2.3 車門確定性優化流程

在isight軟件中搭建車門確定性優化模型，其優化流程如圖4(不包括虛框)所示。利用拉丁超立方試驗設計，不斷調用Hypermesh進行有限元分析，再在Approximation組件中建立RBF模型，并驗證其精度。在Optimization組件中設置設計變量、約束函數及目標函數，選擇序列二次規劃算法不斷尋求最優解[11]。該優化設計為單目標多約束問題，得到設計變量和評價標準的確定性最優解，如表5所示。

表5 確定性優化結果

確定性優化數學模型如下：

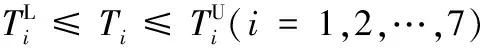
3 車門6σ穩健性優化流程

確定性優化設計結果雖能滿足靜剛度和模態性能的約束條件，但在設計變量波動或噪聲因素干擾時，最優設計點極易超出約束邊界。為充分考慮車門各部件板厚不確定性和材料性能波動的噪聲干擾，本文構建了基于6σ穩健性的單目標多約束車門優化設計方法，優化流程如圖4(包括虛框)所示。

3.1 車門6σ穩健性優化數學模型

選取T1、T2、…、T7、S1、S2為隨機設計變量，考慮彈性模量E和泊松比μ兩個隨機噪聲干擾的影響。設定E、μ屬于正態分布，T1、T2、…、T7的變異系數為0.03，S1、S2、E、μ的變異系數為0.01。車門6σ穩健性優化數學模型如下：

設計變量T1，T2，…，T7，S1，S2

噪聲因素E，μ

minm

maxf

s.t.μ(d1)+6σ(d1)≤2 mm

μ(d2)+6σ(d2)≤2 mm

μ(d3)+6σ(d3)≤2 mm

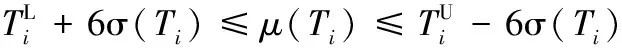
i=1,2, …,10

j=1,2

式中，上標U、L分別表示設計變量的上限和下限。

3.2 基于MCS和NSGAⅡ的6σ穩健性優化

6σ穩健性優化采用雙循環優化策略，即將穩健性分析過程內嵌于確定性優化設計中，并對每一次確定性優化結果采用MCS進行統計評估。與傳統的將多目標轉化成單目標進行優化的算法相比，NSGAⅡ以種群進化為基礎，單次運行找到Pareo解集。本文將NSGAⅡ和MCS相結合，構造出6σ穩健性優化設計流程。

3.3 車門6σ穩健性優化結果

采用多目標遺傳算法對構造的各個代理模型進行近似優化，可得到Patero最優解集。車門的一階固有頻率只要大于38 Hz即可降低與車身發生共振的可能性，要追求車門質量最小化，一階固有頻率最大化，只能從Patero最優解集中挑選最優妥協解，最終的優化結果如表6所示。

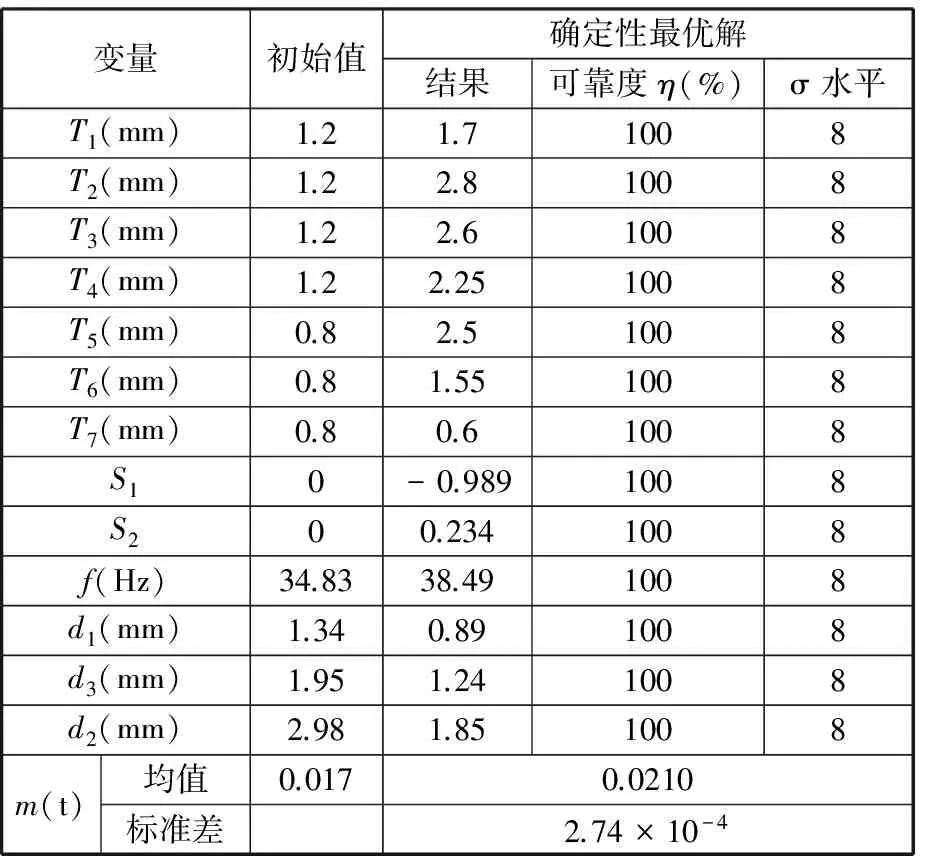
表6 確定性優化結果

對比表5和表6可知，與初始值相比，雖然6σ穩健性最優妥協解的車門質量有所增大，但一階模態頻率增大到38.49 Hz，有效避開了車身一階模態頻率，降低了共振的可能性。其次，6σ穩健性最優解的d1增大了33.6%，d2減小了39.6%，d3減小了34.3%，并且3種約束函數的評價指標均達到了8σ水平，所有設計變量符合正態分布，且在材料噪聲因素的干擾下，約束函數均能在8σ水平的波動內滿足約束條件，設計變量也遠離約束邊界。

與確定性優化TRB車門相比，6σ穩健性最優妥協解大幅度提高了各個約束函數的可靠度。由此可知，6σ穩健性優化在獲得滿足約束條件的同時，可大幅度提高優化設計點的可靠度和穩健性。

4 6σ穩健性優化后TRB車門性能分析

由于非支配解在目標空間的象點是由RBF模型計算得來的，故需進行有限元驗證，根據表5中車門6σ穩健性優化結果設置車門TRB內外板的厚度，并將其代入有限元模型中進行分析計算。

4.1 TRB車門的一階模態

車門自由模態一階振型如圖5所示，與確定性優化結果相比，應用TRB進行6σ穩健性優化后的車門一階模態頻率增大至39.01 Hz，有效避免了共振的可能性。車門窗框下邊緣的最大變形也由原來的41.5 mm減小到38.87 mm，即使發生共振，6σ穩健性優化后的TRB車門也比確定性原始車門的振動幅度小。

4.2 TRB車門下沉剛度

6σ穩健性優化后，TRB車門下沉工況 (CASE1) 下的變形和應力如圖6所示。與確定性優化相比，評價參數節點10 217處的Y向變形d1由0.56 mm增大至0.89 mm，但仍然滿足評價標準，且最大應力發生在載荷加載點——門把手處，其余部分未出現應力集中現象。

圖6 CASE1:變形云圖和應力云圖Fig.6 CASE1: deformation nephogram and stress nephogram

4.3 TRB車門窗框側向剛度

6σ穩健性優化后，TRB車門窗框側向工況(CASE2)下的變形和應力如圖7所示，與確定性優化后TRB車門窗框側向工況下的變形和應力相比，評價參數節點123 562處的X向變形d2由2.56 mm減小至1.85 mm, 最大應力由159 MPa增大至172.3 MPa，除了車門門鎖施加約束載荷處，無應力集中點。

圖7 CASE2:變形云圖和應力云圖Fig.7 CASE2: deformation nephogram and stress nephogram

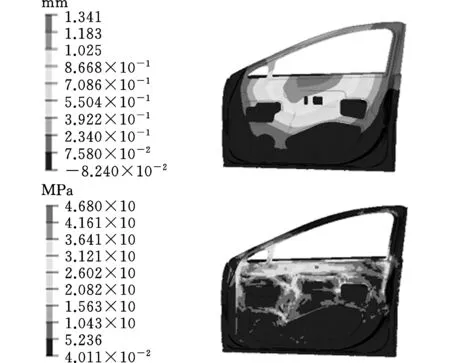
圖8 CASE3:變形云圖和應力云圖Fig.8 CASE3: deformationnephogram and stress nephogram

4.4 TRB車門腰帶擠壓剛度

6σ穩健性優化后，TRB車門腰帶擠壓工況(CASE3)下的變形和應力如圖8所示。與確定性優化后TRB車門腰帶擠壓工況下的變形和應力相比，評價參數節點124 920處的X向變形d3由1.98 mm減小至1.24 mm，最大應力由51.05 MPa減小至46.8 MPa，且應力分布更為均勻，TRB過渡區域無應力集中現象。

將最優妥協解代入RBF模型和有限元模型，得到的參數值如表7所示，RBF模型與有限元模型之間的相對誤差最大為3.13%，最大誤差出現在腰帶擠壓工況，這是因為此工況下的響應非線性程度比較高，因此，基于RBF模型的多目標優化結果的可信度較高。

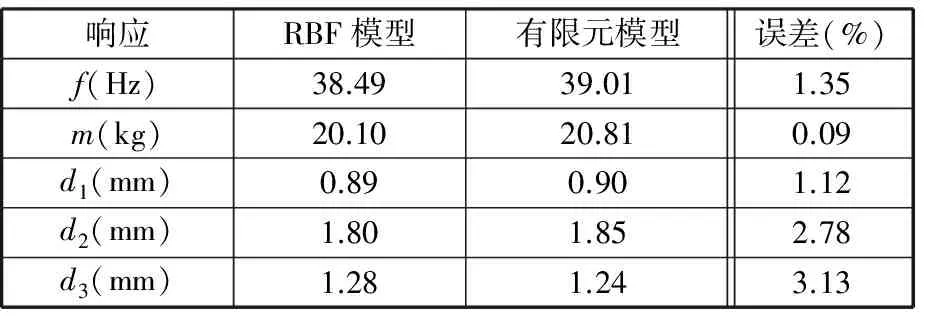
表7 6σ穩健性優化結果驗證

5 結語

將軋制差厚板應用于車門結構優化，將試驗設計、徑向基函數模型、蒙特卡羅模擬法和非支配遺傳算法相結合，構建了基于6σ穩健性的車門軋制差厚板優化設計方法，用徑向基函數模型替代了車門有限元模型，大大提高了整個優化過程的計算效率。優化結果表明，該方法在相對減輕車門質量的同時，能提高車門品質的穩健性，對于板殼類結構的優化設計具有較高的精度、效率和較強的實用性。

[1] 張宇.基于穩健與可靠性優化設計的轎車車身輕量化研究[D].上海：上海交通大學，2009. ZHANG Yu. Research on Lightweight Design of Autobody Structure Using Robust and Reliability-based Design Optimization[D]. Shanghai：Shanghai Jiao Tong University, 2009.

[2] MAGLARAS G, PONSLET E, HALFTKA R T, et al. Analytical and Experimental Comparison of Probabilistic and Deterministic Optimization[J]. AIAA Journal, 1996, 34(7):1512-1518.

[3] GUNAWAN S, AZARM S. Non-gradient Based Parameter Sensitivity Estimation for Single Objective Robust Design Optimization[J]. Journal of Mechanical Design，2004, 126(1):395-402.

[4] GUNAWAN S, AZARM S. Multi-objective Robust Optimization Using a Sensitivity Region Concept[J]. Struct. Multidisc. Optim.，2005, 29(1):50-60.

[5] YOUN B D, CHOI K K, YANG R J, et al. Reliability Based Design Optimization for Crashworthiness of Vehicle Side Impact[J]. Structural and Multidisciplinary Optimization, 2004, 26(3):272-283.

[6] 李玉強，崔振山，陳軍，等. 基于響應面模型的6σ穩健設計方法[J] .上海交通大學學報，2006, 40(2):201-205. LI Yuqiang, CUI Zhenshan，CHEN Jun, et al. Six Sigma Robust Design Methodology Based on Response Surface Model[J]. Journal of Shanghai Jiaotong University, 2006, 40(2):201-205.

[7] 王國春，成艾國，胡成輝，等. 基于 Kriging 模型的汽車前部結構的耐撞性優化[J]. 汽車工程，2011,33(3):208-212. WANG Guochun, CHENG Aiguo, HU Chenghui, et al. Crashworthiness Optimization of Vehicle Frontal Crash Based on Kriging Model[J]. Automotive Engineering, 2011, 33(3):208-212.

[8] 杜平安.有限元網格劃分的基本原則[J]. 機械設計與制造, 2000, 34(3):34-36. Du Ping’an. The Basic Principles of Finite Element Mesh Division[J]. Machinery Design & Manufacture, 2000, 34(3):34-36.

[9] 張勇, 李光耀, 鐘志華.基于移動最小二乘響應面方法的整車輕量化設計優化[J].機械工程學報, 2008,44(11):192-196. ZHANG Yong, LI Guangyao, ZHONG Zhihua. Design Optimization on Lightweight of Full Vehicle Based on Moving Least Square Response Surface Method[J]. Journal of Mechanical Engineering, 2008, 44(11):192-196.

[10] 胥志剛，林忠欽，來新民，等. 面向車身結構輕量化設計的水平集拓撲優化[J]. 上海交通大學學報, 2007, 17(3):26-32. XU Zhigang, LIN Zhongqin, LAI Xinming, et al. A Level Set Topology Optimization Method for Auto-body Structure Lightweight Design[J]. Journal of Shanghai Jiaotong University, 2007, 17(3):26-32.

[11] 黃石華，成艾國，胡朝輝，等. 基于6σ穩健性的拼焊板車門輕量化研究[J]. 汽車工程，2011, 33(3):262-266 HUANG Shihua, CHENG Aiguo, HU Zhaohui, et al. A Research on the Lightweighting of TWB Door Based on Six Sigma Robustnesss[J]. Automotive Engineering, 2011,33(3):262-266.

(編輯 張 洋)

Optimization Design of TRB Car Doors Based on 6σ Robustness

ZHU Maotao1ZHU Caifan1GUO Jiahuan1QIAN Yang2

1.School of Automobile & Traffic Engineering,Jiangsu University,Zhenjiang,Jiangsu,212013 2.Bosch Automotive Products Co.Ltd.，Suzhou,Jiangsu，215100

For car door structure optimization studies, most of them did not consider the car door uncertainty factors. In order to improve robustness of structure optimized car door’s performance, a new type manufacturing process of TRB was applied in car doors, and influences of sheet thicknesses and material performance parameter’s volatility on the robustness of each constraint were considered. Combined with Latin hypercube design and RBF model, using dual cycle optimization strategy of combining Monte Carlo simulation with improved non-dominated sorting genetic algorithm, a TRB car door lightweight design was proposed based on 6σ robustness. This method may obtain an optimal solution, and may improve reliability of design variables and robustness of objective function.

car door; robustness; tailor rolled blank(TRB); Monte Carlo simulation; lightweight

白振華，男，1975年生。燕山大學國家冷軋板帶裝備及工藝工程技術研究中心及燕山大學亞穩材料制備技術與科學國家重點實驗室教授、博士研究生導師。主要研究方向為機械設計及自動化、軋鋼設備及工藝、板形控制及自動化。獲國家科技進步一等獎1項，省部級科技進步一等獎 3項，省部級科技進步二等獎3項，省部級科技發明二等獎2項，省部級科技進步三等獎4項。出版學術專著2部，發表論文80余篇。E-mail：bai_zhenhua@aliyun.com。李麒麟，男，1993年生。燕山大學國家冷軋板帶裝備及工藝工程技術研究中心碩士研究生。劉亞星，男，1990年生。燕山大學國家冷軋板帶裝備及工藝工程技術研究中心碩士研究生。崔亞亞，男，1988年生。燕山大學國家冷軋板帶裝備及工藝工程技術研究中心碩士研究生。郭振勝，男，1975年生。山東冠洲股份有限公司技術部部長。宋章峰，男，1970年生。山東冠洲股份有限公司技術部總經理。

2016-06-28

江蘇省汽車工程重點實驗室資助項目(1851120141)

U463.834

10.3969/j.issn.1004-132X.2017.08.020