含多條裂紋梁的模態與振動疲勞壽命分析*

馬一江， 陳國平

(南京航空航天大學機械結構力學及控制國家重點實驗室 南京, 210016)

?

含多條裂紋梁的模態與振動疲勞壽命分析*

馬一江， 陳國平

(南京航空航天大學機械結構力學及控制國家重點實驗室 南京, 210016)

基于Paris公式，提出了一種含多條裂紋梁疲勞壽命預估的方法。在模態分析中，基于傳遞矩陣方法，利用無質量的彎曲彈簧等效裂紋，提出一種求解含有多條裂紋梁固有振型的方法,分析裂紋數目、裂紋位置、裂紋深度對裂紋梁固有頻率的影響。在振動疲勞分析中，研究了在簡諧激勵作用下裂紋數目對裂紋尖端應力強度因子的影響。通過Paris疲勞裂紋擴展方程和同步分析法，考慮裂紋梁振動與裂紋擴展的相互作用，分析了裂紋數目和裂紋位置對裂紋梁疲勞壽命的影響。結果表明,裂紋數量、裂紋位置和深度對梁的模態參數和疲勞壽命有重要影響。

裂紋梁；傳遞矩陣法；固有頻率；振動疲勞

引 言

工程結構一般處于振動環境中，振動產生的裂紋引起的疲勞破壞是大型工程結構失效的重要原因之一。含裂紋結構作為工程中大型結構的重要組成部分并大量使用，很多學者在這類結構的振動分析方面進行了大量的研究分析。由于加工和裝配等原因，梁表面可能存在初始損傷。目前，針對含有單條裂紋梁結構的振動分析取得了一定的成果[1-3]；但是裂紋數目的增加導致裂紋梁結構的特征行列式的階數增加，因此而針對含有多條裂紋梁結構的振動分析則面臨很大的困難，很多學者針對含有多條裂紋梁的振動分析也進行了大量的研究[4-5]。Shifrin等[6]提出了一種新方法來求解含有多條橫向裂紋梁的固有振型，這種方法大大縮減了裂紋梁特征行列式的階數，使得多裂紋梁結構的振動分析大大簡化。

隨著斷裂力學的發展，1960年前后，波音公司最先發現應力強度因子在疲勞裂紋擴展中起關鍵作用。1963年，Paris等[7]將疲勞裂紋擴展數據與應力強度因子幅值進行對比，發現疲勞裂紋擴展是由裂紋尖端應力強度因子幅值所控制的，由此開創疲勞斷裂理論。張立軍[8]利用變參數Weibull模型研究了寬帶隨機載荷作用下結構件的疲勞壽命，提高了疲勞壽命預測的精度。文獻[9-11]也提出很多估算疲勞壽命的方法。利用這些方法，在已知裂紋尖端位置應力場的情況下，就能確定裂紋擴展到疲勞破壞時所要經歷的振動循環次數。然而在這類疲勞破壞分析中，主要采用靜力學方法來進行應力分析，忽略了疲勞裂紋擴展引起的結構固有振型的變化，使得結構疲勞壽命的預估與工程實際相差很大,因此結構動響應分析應該考慮疲勞裂紋擴展與振動的相互作用。劉文光等[12]基于Paris方程采用同步分析法研究了懸臂梁根部單條裂紋情況下懸臂梁的疲勞壽命,但是沒有考慮裂紋相對位置和裂紋數目對疲勞壽命的影響。在工程實際中，結構損傷可能有很多處，也可能出現在懸臂梁表面的任意位置，所以振動和疲勞壽命分析時應該考慮裂紋數目和相對位置的影響。

筆者對含有多條橫向裂紋懸臂梁進行了模態分析，用無質量的彎曲彈簧來代替結構裂紋，根據斷裂力學的理論，推導了含多條裂紋梁的特征方程。通過數值模擬，分析了裂紋位置、裂紋深度和裂紋數量對梁固有頻率的影響。在振動疲勞分析中，分析了裂紋數目對裂紋尖端應力場強度的影響。基于Paris疲勞裂紋擴展方程，考慮裂紋梁振動與裂紋擴展的相互影響，采用同步分析方法，分析了裂紋數目和裂紋相對位置對裂紋梁疲勞壽命的影響，為含多條裂紋梁結構的疲勞壽命預測提供了一種方法。

1 模型建立

如圖1所示，理論分析對象為一個等截面矩形梁，長為L，寬為b，高為h，梁表面存在n條橫向裂紋，每條裂紋離固定端的位置分別為L1，L2，…，Ln。

根據Dimarogonas和Paipeties[13]理論，該裂紋梁內每條裂紋的局部柔度可以表示成如下形式

(1)

其中：E為梁材料的彈性模量;I為梁橫截面的慣性矩;ri=ai/h為第i條裂紋的相對裂紋深度;ai為第i條裂紋的深度;f(ri)為第i條裂紋的局部柔度函數，可以由應變能密度函數求得

(2)

2 模態分析

以各條橫向裂紋為端點，整段梁被n條裂紋分成n+1段完整梁，每段梁的長度分別為l1，l2，…，ln+1，根據Bernoulli-Euler理論，每段梁的無阻尼彎曲振動微分方程為

(3)

方程(3)的解可以表示為

(4)

其中：

根據材料力學，可以推導出如下關系式

在任意一段梁的兩端截面，應用以上關系式，可以得到

改寫成矩陣形式，可得

DR=TiDL

(5)

其中：Ti稱為該多裂紋梁第i段的傳遞矩陣；li為該多裂紋梁第i段長度。

方程(4)中的待定系數可以表示為

(6)

即可得到每段梁的振型函數。

在該多裂紋梁的每條裂紋位置，根據撓度、彎矩和剪力的連續性和轉角的相容關系，裂紋的左右兩邊截面的撓度、轉角、彎矩和剪力可以表示為

(7)

改寫成矩陣形式

DR=SiDL

(8)

其中：Si為該多裂紋梁第i條裂紋位置的傳遞矩陣。

因此，對于整個多裂紋梁，右端狀態矢量和左端狀態矢量間的傳遞關系可以表示為

DN=HD1

(9)

其中：H為含n條裂紋梁的傳遞矩陣。

H=Tn+1SnTnSn-1…T2S1T1

(10)

一般情況下，在導入邊界條件時，其中兩個邊界條件為零，因此可以推導出一個2×2的特征矩陣H1，使得本方法在求解多裂紋梁的固有頻率時分析過程大大簡化，則該裂紋梁的頻率方程為

detH1=0

(11)

這樣由方程(11)可求得該裂紋梁的任意階固有頻率，對應的固有振型可通過方程(4)獲得。

3 振動疲勞分析

3.1 動力學響應分析

假設該裂紋梁為一個左端固定、右端自由的懸臂梁，在梁的自由端作用垂直方向的簡諧激勵F0eiωt。隨著裂紋的擴展，結構的動態特性是時變的，因此取該裂紋梁結構的某一瞬態進行分析，則對應的邊界條件為

(12)

將方程組(12)代入式(9)，可以得到第1段梁固定端位置的撓度W1(0)、轉角θ1(0)、彎矩M1(0)和剪力Q1(0)；將得到的這些初始值再代入方程(6)，可以得到第1段梁振型函數對應的系數c11，c12，c13，c14，即可求得第1段梁的振型函數。依次類推，可以得到該裂紋梁上任意段梁的振型函數。

由于圖(1)中，該梁上的橫向裂紋屬于工程中最常見且破壞程度最嚴重的裂紋形式——張開型(I型)裂紋，所以以I型裂紋為研究重點。根據HOOKE定律

(13)

對于第i段梁，長度為li，可以得到該段梁表面的動應力響應

(14)

其中：y為梁表面離梁中面的距離。

(15)

則該段裂紋梁右端，即裂紋尖端的應力強度因子表達式為

(16)

其中：ai為第i條裂紋的深度。

根據本研究的裂紋類型和加載形式[14]，形狀函數為

(17)

3.2 基于斷裂理論的振動疲勞分析

3.2.1 動應力強度因子

動應力強度因子是在振動環境下表征裂紋尖端應力場分布的物理量，裂紋尖端動應力強度因子的一般表達式為

(18)

其中：ΔKI為動應力強度因子的振幅；Δσd為動應力的振幅；a為裂紋長度；Y(ri)為形狀函數(與裂紋大小、位置有關)。

若該梁受到簡諧激勵作用，并且裂紋為I型(張開型)裂紋，則裂紋尖端的動應力強度因子振幅可表示為

(19)

將式(15)代入式(19)，即可得到任意條裂紋尖端動應力強度因子振幅的表達式：

(20)

3.2.2 疲勞裂紋擴展速率

Paris公式，或稱疲勞裂紋擴展方程，是疲勞壽命預測應用最廣泛且最簡單的公式。該公式建立了疲勞裂紋擴展速率與動應力強度因子振幅ΔK之間的關系，為疲勞斷裂問題的研究開辟了最主要的途徑。在線彈性斷裂力學范圍內中等應力狀態下，Paris公式能較好地預測直裂式裂紋結構的疲勞壽命。Paris公式的表達式為

(21)

其中：C，n為材料常數；da/dN表示直裂式裂紋的疲勞擴展速率。

因此利用Paris方程來模擬該裂紋懸臂梁疲勞裂紋的擴展，將式(20)代入式(21)，即可得到任意條裂紋的疲勞擴展速率模型

(22)

3.2.3 疲勞裂紋擴展分析

研究表明：在簡諧激勵作用下，結構的受迫振動會導致疲勞裂紋的擴展；結構疲勞裂紋的擴展同樣會改變結構原有的動態特性，從而導致裂紋尖端區域應力場分布發生變化，并最終影響裂紋的疲勞擴展速率。兩者之間存在相互作用，并相互影響。因此，筆者采用同步分析方法，即裂紋懸臂梁的振動模態分析與疲勞裂紋擴展壽命的估算同步進行。假設在每一個振動周期內裂紋的相對深度是不變的，裂紋擴展發生在每一個振動周期結束時。

具體的步驟是，假設該裂紋梁每振動一周計算出的動應力幅值為一個恒定值，利用式(22)計算周期載荷作用下，裂紋梁每振動ΔNj周的任意條裂紋的疲勞擴展增量

(23)

其中：Δaij為第i條裂紋第j次循環的裂紋增量；ΔNj=Nj-Nj-1。

取ΔNj=1，則有

da/dN≈Δaj/ΔNj

(24)

所以，裂紋梁上第i條裂紋第j次循環的裂紋增量的表達式為

(25)

結構受到恒定振幅簡諧激勵作用時，裂紋的最終深度可通過疊加法計算，表達式為

(26)

其中：ai0為裂紋梁上第i條裂紋的初始深度；k為總振動循環次數；aik為第i條裂紋振動k次之后的裂紋總深度。

3.2.4 疲勞裂紋失效判據

為了判斷該裂紋懸臂梁是否失效，現采用以下準則作為失效判據。

準則1：如果該裂紋懸臂梁上任意條裂紋擴展至梁的中面時，就認為該結構已經破壞

ai≥ac

(27)

其中：ac為臨界裂紋長度，取ac=h/2。

準則2：如果該裂紋懸臂梁上任意一條裂紋尖端應力強度因子大于材料的斷裂韌性，就認為該結構已經發生失穩斷裂

(28)

其中：Kc為材料的斷裂韌性；Kmax為最大應力強度因子。

4 數值算例與結果分析

4.1 多處裂紋對梁固有頻率的影響

4.1.1 裂紋數目對梁固有頻率的影響

固定該裂紋懸臂梁上一條裂紋的相對位置為L1/L=0.1，初始裂紋深度為a10=0.002 m。

若該裂紋梁上僅有一條裂紋時，即為該固定的裂紋。若該裂紋梁上有兩條裂紋時，第1條裂紋為該固定裂紋；第2條裂紋的相對位置為L2/L=0.3，初始裂紋深度為a20=0.002 m。若該裂紋梁上有3條裂紋時，第1條裂紋為該固定裂紋；第2條裂紋的相對位置為L2/L=0.3，初始裂紋深度為a20=0.002 m；第3條裂紋的相對位置為L3/L=0.5，初始裂紋深度為a30=0.002 m。3種情況對應的第1階固有頻率列入表1中。

若將該固定裂紋的相對位置改為L1/L=0.15，其他情況不變。3種情況對應的第1階固有頻率列入表1中。

若將該固定裂紋的相對位置改為L1/L=0.2，其他情況不變。3種情況對應的第1階固有頻率列入表1中。

表1 裂紋條數不同時裂紋梁的固有頻率

Tab. 1 Natural frequencies of the cracked beam with different number of cracks Hz

表1數據顯示，固定裂紋懸臂梁上某一裂紋的相對位置和深度，隨著裂紋條數的增加，裂紋梁固有頻率逐步減小。在裂紋數目、相對位置和深度都相同時，隨著第1條裂紋遠離懸臂梁固定端，該裂紋梁第1階固有頻率逐步增大。

4.1.2 裂紋相對位置和深度對裂紋梁固有頻率的影響

1) 假設該裂紋懸臂梁,僅有兩條橫向裂紋，第1條裂紋的深度為a10=0.002 m，第2條裂紋的深度為a20=0.002 m，兩條裂紋在不同位置時對應的固有頻率如圖2所示。

圖2 裂紋深度一定時，裂紋梁第1階固有頻率隨著裂紋相對位置的變化規律Fig.2 Variation of the first order natural frequencies of the cracked beam along with the position of the cracks

由圖2可以得到，隨著兩條裂紋中任意一條裂紋逐漸遠離固定端，該裂紋梁的固有頻率均逐漸增大；當兩條裂紋非常接近時，該裂紋梁的固有頻率相對較大。

2) 假設該裂紋懸臂梁僅有兩條橫向裂紋，第1條裂紋的相對位置為L1/L=0.1，第2條裂紋的相對位置為L2/L=0.5，兩條裂紋在不同深度時，該裂紋懸臂梁第1階固有頻率的變化規律如圖3所示。

由圖3可以得到，隨著該裂紋梁上兩條橫向裂紋中任意一條裂紋相對深度的逐步增大，該裂紋梁的第1階固有頻率逐步減小；第1條裂紋(靠近懸臂梁固定端的裂紋)的深度變化對該裂紋梁固有頻率的變化影響比較大，隨著第1條裂紋深度的增加，該梁第1階固有頻率減小的幅度較大。

4.2 多處裂紋對裂紋尖端應力強度因子的影響

假設在該裂紋懸臂梁的自由端作用一個垂直方向的簡諧激勵，激勵幅值為50 N，激勵頻率為裂紋梁的固有頻率。裂紋的條數、相對位置和深度與章節4.1.1完全相同，則得到第1條裂紋尖端應力強度因子的值列入表2中。

圖3 裂紋相對位置固定時，裂紋梁第一階固有頻率隨著裂紋深度的變化規律Fig.3 Variation of the first order natural frequencies of the cracked beam along with the depth of the cracks

表2 裂紋條數不同時，裂紋梁第1條裂紋尖端應力強度因子

Tab. 2 Stress intensity factors at the first crack tip of the cracked beam with different number of cracks

裂紋數目L1/L=0．1L1/L=0．15L1/L=0．217．6209×1076．9851×1076．3558×10727．6747×1077．0359×1076．4032×10737．6965×1077．0564×1076．4224×107

表2數據顯示，固定裂紋懸臂梁上第1條裂紋(靠近固定端的裂紋)的相對位置和深度隨著裂紋條數的增加，該裂紋梁第1條裂紋尖端應力強度因子的值逐步增大。在裂紋數目、相對位置和深度相同時，隨著第1條裂紋逐漸遠離該懸臂梁固定端，該裂紋梁第1條裂紋尖端應力強度因子也逐步減小。

4.3 多處裂紋對梁疲勞壽命的影響

假設在該裂紋懸臂梁的自由端作用一個垂直方向的簡諧激勵，激勵幅值為50 N，保持不變。

4.3.1 共振狀態下阻尼對梁疲勞壽命的影響

假設該裂紋懸臂梁僅有一條裂紋，且該裂紋的相對位置為L1/L=0，初始裂紋深度為a10=0.002 m。則當該裂紋懸臂梁處于共振狀態下，阻尼損耗因子分別為γ=0.005，γ=0.01，γ=0.05，γ=0.1時，該裂紋懸臂梁的疲勞壽命如圖4所示。

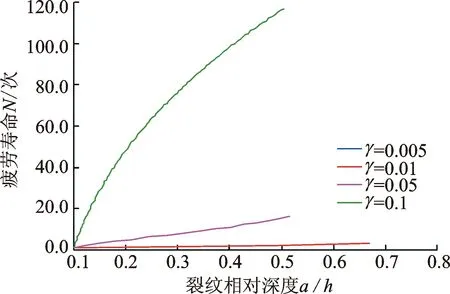
圖4 共振狀態下，不同阻尼時該裂紋梁的疲勞壽命Fig.4 Fatiguelives of the cracked beam with different damping loss factors at resonance conditions

由圖4可見，阻尼損耗因子對共振情況下裂紋梁的疲勞壽命影響非常大。其中當阻尼損耗因子為γ=0.005和γ=0.01時，裂紋梁的疲勞壽命曲線出現重合，因此只顯示γ=0.01時的曲線。隨著阻尼損耗因子的逐漸減小，該裂紋梁的共振疲勞壽命逐漸較小。與文獻[12]得到的結論相同，同時圖4與文獻[12]中的圖3基本相同，只是在疲勞壽命的數值上有很小的誤差。因此，可以證明筆者提出的多裂紋梁疲勞壽命預測的方法是可行的。

4.3.2 共振狀態下裂紋條數對梁疲勞壽命的影響

假設裂紋的條數、相對位置和深度與4.1.1節完全相同，若該裂紋梁始終處于共振狀態下，得到疲勞壽命值列入表3中。

表3 共振狀態下裂紋條數不同時裂紋梁的振動疲勞壽命

Tab.3 Fatigue lives of the beam with different number of cracks at resonance conditions 次

表3的數據顯示，固定裂紋梁上第1條裂紋的相對位置和深度，隨著裂紋條數的增加，該裂紋梁共振疲勞壽命逐步減小。根據4.2節的結論，隨著裂紋條數的增加，裂紋尖端應力強度因子逐步增大，由式(25)可以得到每循環的裂紋增量也相應增大，導致疲勞壽命逐步減小。由于第1條裂紋尖端的應力強度因子的值最大，所以第1條裂紋決定著該裂紋梁的疲勞壽命，表3中，隨著第一條裂紋遠離懸臂梁的固定端，該裂紋梁的疲勞壽命逐步增大。

4.3.3 激勵頻率恒定的情況下裂紋條數對梁疲勞壽命的影響

假設裂紋的條數、相對位置和深度與4.1.1節完全相同，外激勵頻率為遠離第1階固有頻率100，500，1 000和1 500 Hz得到的疲勞壽命值列入表4中。

表4 恒定激勵頻率下不同裂紋條數時裂紋梁的疲勞壽命

Tab.4 Fatigue lives of the cracked beam with different number of cracks under constant excitation frequencies 次

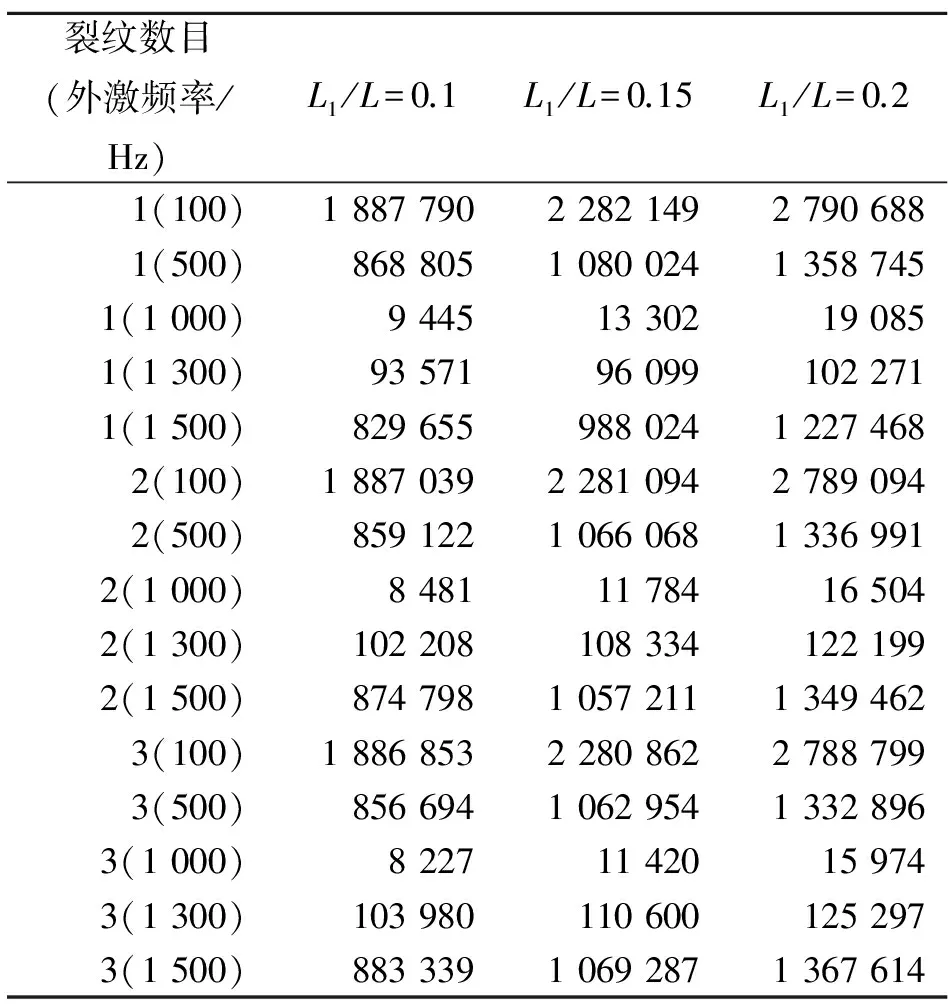
由表4的數據可以得到以下結論。

1) 裂紋梁上第1條裂紋的相對位置決定該梁的疲勞壽命。

2) 在外激勵頻率恒定的情況下，隨著第1條裂紋的相對位置遠離該裂紋梁固定端，該梁的疲勞壽命逐步增大。

3) 在外激勵頻率恒定的情況下，當外激勵頻率接近第1階固有頻率時，該裂紋梁的疲勞壽命顯著減小；當外激勵頻率遠離第1階固有頻率時，該裂紋梁的疲勞壽命顯著增大。

4) 在外激勵頻率小于固有頻率的情況下，隨著裂紋條數的增加，裂紋梁的固有頻率逐步減小，使得此時的外激頻率逐步接近固有頻率，因而裂紋梁的疲勞壽命逐漸減小；在外激勵頻率大于固有頻率的情況下，隨著裂紋條數的加，裂紋梁的固有頻率逐步減小，使得此時的外激頻率逐步遠離固有頻率，因而裂紋梁的疲勞壽命逐漸增大。

5 結束語

在含多裂紋的梁上，在固定裂紋梁上某條裂紋的相對位置和深度時，隨著裂紋條數的增加，裂紋梁固有頻率逐步減小。在含雙裂紋的梁上，隨著裂紋梁上的任意一條裂紋遠離固定端，該裂紋梁固有頻率逐步增大；且第1條裂紋(靠近懸臂梁固定端的裂紋)的深度變化對該裂紋梁固有頻率的變化影響比較大。

在外激勵作用下，當裂紋梁處于共振狀態時，固定裂紋懸臂梁上某一裂紋的相對位置和深度，隨著裂紋條數的增加，該裂紋尖端應力強度因子的值逐步增大；隨著第1條裂紋逐步遠離固定端，該裂紋尖端應力強度因子的值逐步減小。在簡諧激勵作用下，固定裂紋梁上第1條裂紋的相對位置和深度，隨著裂紋條數增加，該裂紋梁共振疲勞壽命逐步減小。

在恒定外激勵頻率小于固有頻率的情況下，隨著裂紋條數的增加，裂紋梁的固有頻率逐步減小，使得此時的外激頻率逐步接近固有頻率，因而裂紋梁的疲勞壽命逐漸減小；在恒定外激勵頻率大于固有頻率的情況下，隨著裂紋條數的增加，裂紋梁的固有頻率逐步減小，使得此時的外激頻率逐步遠離固有頻率，因而裂紋梁的疲勞壽命逐漸增大。

[1] Krawczuk M. Natural vibration of rectangular plates with a through crack[J]. Archive Applied Mechanics, 1993, 63(7): 491-504.

[2] Qian Guanliang, Gu Songnan, Jiang Jiesheng. The dynamic behaviour and crack detection of a beam with a crack[J]. Journal of Sound and Vibration, 1990, 138(2): 233-243.

[3] Morassl A. Crack-induced changes in eigen-frequencies of beam structures[J]. Journal of Engineering Mechanics, 1993, 119(9): 1768-1803.

[4] Ostachowicz W M, Krawczuk M.Analysis of the effect of cracks on the natural frequencies of a cantilever beam[J]. Journal Sound and Vibration, 1991, 150(2): 191-201.

[5] Hu Jialou, Liang R Y. An integrated approach to detection of cracks using vibration characteristics[J]. Journal of the Franklin Institute, 1993, 330(5): 841-853.

[6] Shifrin E I, Ruotolo R. Natural frequencies of a beam with an arbitrary number of cracks[J]. Journal of Sound and Vibration, 1999, 222(3): 409-423.

[7] Paris P C, Erdogan F A. Critical analysis of crack propagation laws.[J]. Journal of Basic Engineering, 1963, 85(4):528-534.

[8] 張立軍. 寬帶隨機載荷下的疲勞壽命統一模型[J]. 振動、測試與診斷, 2014, 34(6):1022-1026.

Zhang Lijun. Unified model of fatigue life under wide-band random load[J]. Journal of Vibration, Measurement and Diagnosis,2014,34(6):1022-1026. (in Chinese)

[9] Ponomarev P V, Lopatin A D.Calculation of the fatigue fracture under the influence of dynamic loads [J]. International Applied Mechanics, 1972, 8(6): 613-617.

[10] Shih Y S, Wu G Y. Effect of vibration on fatigue crack growth of an edge crack for a rectangular plate[J]. International Journal of Fatigue, 2002, 24(5): 557-566.

[11] Schlums D H. Fatigue testing and crack analysis of resonating structures[D]. Zürich: Swiss Federal Institute of Technology, 2001.

[12] 劉文光，陳國平.含裂紋懸臂梁的振動與疲勞耦合分析[J].振動與沖擊，2011，30(5)：140-144.

Liu Wengguang, Chen Guoping. Coupling analysis for vibration and fatigue of a cracked cantilever beam[J]. Journal of Vibration and Shock, 2011, 30(5): 140-144. (in Chinese)

[13] Dimarogonas A D, Paipetis S A, Chondros T G. Analytical methods in rotor dynamics[M]. London: Applied Publishers, 2013：221-250.

[14] Tada H, Paris P C, Trwin G R. The stress analysis of cracks handbook[M]. Pennsylvania: Del Research Corporation Hellertown, 1973:82-232.

[15] Dentsoras A J, Dimarogonas A D. Resonance controlled fatigue crack propagation in a beam under longitudinal vibration[J]. International Journal of Fatigue, 1983, 23(1): 15-22.

*江蘇高校優勢學科建設工程基金資助項目(PAPD)

2015-03-26；

2015-05-21

TH114; V224

馬一江，男，1989年8月生，博士生。主要研究方向為損傷結構動力學、損傷結構壽命預測。 E-mail:yima@nuaa.edu.cn

陳國平，男，1956年7月生，博士、教授、博士生導師。研究方向為復雜結構動力學。 E-mail:gpchen@nuaa.edu.cn