量測不確定的四元數約束CKF姿態估計

黃 蔚

(中國艦船研究設計中心，武漢430064)

量測不確定的四元數約束CKF姿態估計

黃 蔚

(中國艦船研究設計中心，武漢430064)

針對姿態估計系統在量測不確定和四元數約束下存在發散及估計精度差的缺陷，提出了一種基于不確定量測的四元數約束容積卡爾曼濾波算法(quaternion constrained cubature Kalman filter based on uncertain measurements, UCCKF).該算法克服了約束容積卡爾曼濾波算法的局限性，采用獨立的伯努利隨機變量來描述量測的不確定性，利用三階球面-相徑容積規則近似計算非線性函數的后驗均值和協方差.并針對四元數規范化問題，采用兩步投影理論來解決四元數約束限制.仿真結果表明，相比較于約束容積卡爾曼濾波(constrained cubature Kalman filter, CCKF)和無跡混合濾波 (unscented mixture filter, UMF)，提出的UCCKF算法在量測不確定情況下具有更好的收斂性和更高的估計精度，說明該算法對量測不確定下的非線性姿態估計系統是有效、可行的.關鍵詞: 姿態估計；四元數約束；不確定量測；容積卡爾曼濾波；兩步投影理論

針對由星敏感器和陀螺組成的姿態估計系統，四元數因計算量小、非奇異性及可全姿態工作等優點常被作為其姿態描述參數[1].因此，基于四元數非線性姿態估計濾波技術成為研究熱點[2-4].由于四元數存在歸一化約束限制，許多處理四元數約束的非線性姿態估計算法被提出，主要分為以下幾種：1)四元數強制性約束方法，如范數限制卡爾曼濾波算法[5]、平方根四元數CKF[6]等；2) 將誤差四元數作為狀態變量，對模型進行降階處理，轉化為無約束的姿態估計模型，如乘性擴展卡爾曼濾波算法[7]；3)將四元數看成是一個旋轉矢量，與濾波算法相結合，如四元數狀態切換無跡卡爾曼濾波器[8]等；4) 將四元數參數與其他無冗余的三維姿態參數進行切換，如無跡四元數估計法[9]等.其中，兩步投影理論[6,10]是一種有效的方法，將狀態估計值分兩步投影到約束表面，從而解決四元數規范化問題.

上述研究四元數非線性姿態估計，都是基于準確的量測模型.而在實際應用中，由于光學成像、星圖識別等復雜的處理步驟以及網絡傳輸的不可靠性，導致姿態信息輸出突然失效，從而引起星敏感器量測丟失現象的發生[11-12]，這在狀態空間模型上體現為量測模型不確定.此種情況下，基于四元數姿態估計濾波方法研究相對較少.文獻[13]針對量測模型不確定的情況采用協方差分配的方法來求取狀態估計值.而文獻[14]在此基礎上，采用校正擴展和無跡卡爾曼濾波相結合的方法，雖然能有效解決量測丟失問題，但無跡卡爾曼濾波算法在高維情況下存在算法穩定性差，濾波精度低的現象，同時未考慮四元數約束.而CKF算法采用三階球面-相徑容積規則[15]產生一組容積點來近似非線性函數的后驗分布，相比較于無跡卡爾曼濾波算法，CKF算法具有嚴格的數學理論支撐，針對高維系統，不存在采樣非局部效應，濾波算法的數值穩定性更好，濾波估計精度更高.

基于此，本文在推導基于不確定量測的誤差四元數非線性姿態估計模型基礎上，提出一種基于不確定量測的四元數約束容積卡爾曼濾波姿態估計算法(quaternion constrained cubature kalman filter based on uncertain measurements, UCCKF)，并通過仿真驗證了該算法在量測不確定情況下的有效性.

1 不確定量測的非線性姿態估計模型

1.1 陀螺測量模型

一個連續形式的陀螺測量模型可表示為

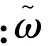
1.2 系統狀態方程

根據文獻[1]，基于四元數的飛行器軌道動力學方程能夠被描述為

(1)

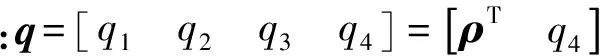
由上述四元數描述的姿態矩陣為

利用四元數乘法，誤差四元數能夠被定義為

(2)

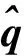
(3)

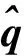
(4)

(5)

由于

(6)

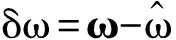
(7)

然后利用式(5)、(6)、(7)可得

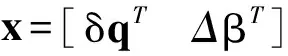
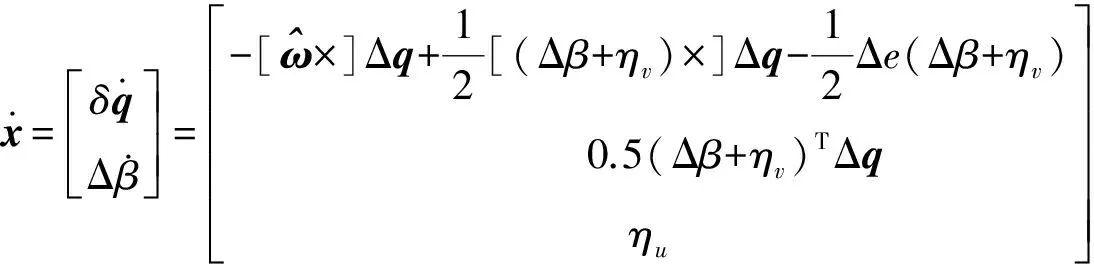
(8)

將式(8)進行離散化得姿態估計系統離散狀態方程為

(9)

式中wk均值為零，方差為Qk的高斯白噪聲.

1.3 系統量測方程

若星敏感器的輸出為光軸在本體坐標系上的參考矢量，則星敏感器測量模型表示為

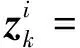
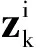
式中:zk為星敏感器的輸出矢量；h(xk)為非線性量測函數；vk為高斯白噪聲，其均值為零，方差為Rk.

如果考慮星敏感器的量測存在丟失或是不確定的情況，則帶量測不確定的星敏感器測量模型為

(10)

式中：λk表示描述量測中的不確定性，作為獨立的伯努利隨機變量，取值為0或1，P[λk=1]=pk表示量測沒有出現錯誤的概率，則λk的均值和方差分別為pk和(1-pk)pk.

2 UCCKF算法

2.1 三階球面-相徑容積規則

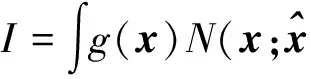
1)將Px進行Cholesky分解.

Px=SST.

2)容積點的求取.

(11)

式中：m=2n；假設n維的單位向量用e=[1,0,…,0]T來表示，任意改變e中元素的符號或是對其元素進行全排列得到的所有單位向量的集合表示為點集[1]，則[1]i就為點集[1]中的第i個點；ξi為第i個容積點；ωi為相應容積點的權值.

3)容積點經過非線性函數的傳遞值為

2.2 不確定量測的統計特性

針對式(10)的不確定量測，由于λk、xk以及vk是相互獨立的，則zk的均值、方差以及互協方差分別為：

E[zk]=E[λkh(xk)+vk]=pkE[h(xk)],

(12)

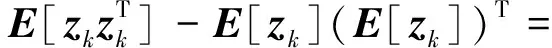
(13)

Cov(xk,zk)=Cov(xk,λkh(xk)+vk)=Cov(xk,λkh(xk))=pkCov(xk,h(xk)).

(14)

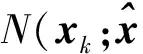
(15)

(16)

(17)

式中χi為容積點，ωi為相應的權值，可以根據式(11)求出.

2.3 UCCKF算法

針對由式(9)和式(10)組成的非線性姿態估計系統，同時考慮量測不確定和四元數約束兩種情況，并利用三階球面-相徑容積規則近似非線性函數的后驗均值和協方差，給出了一種UCCKF算法.其算法流程如下.

2.3.1 時間更新

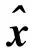
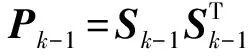
將上述容積點經狀態非線性函數的傳遞值為

2.3.2 量測更新

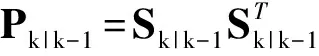
將上述容積點經量測非線性函數的傳遞值為

由式(15)～(17)可以求出關于y=h(xk)的統計特性，其均值、方差以及互協方差為：

再根據式(12)～(14)可以求出不確定量測下zk的均值、方差以及互協方差為：

則無四元數約束下的狀態估計及協方差為：

(18)

(19)

2.3.3 兩步投影理論

由于四元數存在歸一化的限制，即姿態估計系統的部分狀態量存在四元數約束情況，如果不考慮狀態約束直接作濾波處理，濾波精度差，甚至會導致協方差奇異.因此需要對濾波方法進行改進，而文獻[2]的強制性約束只是簡單的將姿態估計值投影到四元數約束表面，對姿態估計方差沒有調整，這會引起濾波精度的下降，由于四元數約束本質上是屬于非線性等式約束，因此，本文采用文獻[10]提出的兩步投影理論來解決非線性四元數約束問題.第1步投影將無約束的狀態估計分布投影到約束表面，使得姿態估計分布滿足四元數約束，但是這會引起姿態估計方差的下降.第2步投影則將約束的狀態估計分布投影到約束表面，使得姿態估計均值滿足四元數約束，同時對姿態估計方差進行補償，從而在保證四元數規范化的同時提高姿態估計的精度.

由于狀態變量xk中，誤差四元數δq滿足約束c(xk)=δqTδq-1，則將無約束狀態投影到約束表面為

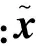
利用兩步投影理論對式(18)、(19)中未約束的狀態估計進行處理.

第1步投影 為使無約束狀態估計分布滿足非線性等式約束，將其投影到約束表面，從而得到約束的狀態估計分布均值和方差分別為：

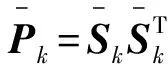
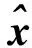
從上述推導可以看出，當p=1，即不存在量測不確定情況，則UCCKF退化為約束容積卡爾曼濾波(constrained cubature Kalman filter, CCKF).

3 仿真實驗及分析

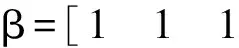
基于上述仿真實驗平臺，為更好驗證本文提出的UCCKF算法的有效性，將其與CCKF算法以及文獻[14]中的無跡混合濾波算法(unscented mixture filter, UMF)進行比較和分析.同時，UMF算法用于非線性姿態估計系統，需考慮四元數約束，因此，在其每步狀態更新后加上強制性的四元數約束.仿真時間設為800 s.仿真結果如圖1～3所示.

圖1、2顯示的是當星敏感器未出現量測丟失的概率分別為p=0.1和p=0.5時濾波得到的姿態誤差對比圖.從這兩個圖中可以明顯看出，CCKF濾波算法隨著仿真時間的增加姿態誤差不斷增大，而UMF算法和本文提出的UCCKF算法則未出現明顯的濾波發散現象，算法較為穩定，算法收斂精度都能達到20 arcsec.同時隨著星敏感器未出現量測丟失的概率p不斷增大，這3種算法的濾波精度均有所提高.這些現象出現的原因是CCKF濾波算法設計未考慮量測丟失的影響從而導致在出現量測丟失的情況下濾波算法不穩定，估計精度降低.而UMF算法和UCCKF算法均在算法設計中考慮了量測丟失的影響，當星敏感器量測丟失出現時，算法均能收斂，保持穩定.圖3顯示的是當星敏感器未出現量測丟失的概率p=0.8時姿態誤差的對比圖，從圖3中可以看出，3種算法均能收斂，估計精度相當.這是由于星敏感器出現正確量測的概率較高，因此對CCKF算法的影響減小，CCKF算法能夠收斂，且估計精度影響不大.

為了體現算法比較的公正性以及更好地比較算法穩態時的估計性能，姿態角的均方根誤差(root-mean square error, RMSE)被采用來描述姿態估計的質量，它被定義為

式中:aei(k)為第i次蒙特卡羅仿真姿態誤差向量；NMC為蒙特卡羅仿真的總次數，仿真中將其設為NMC=50.

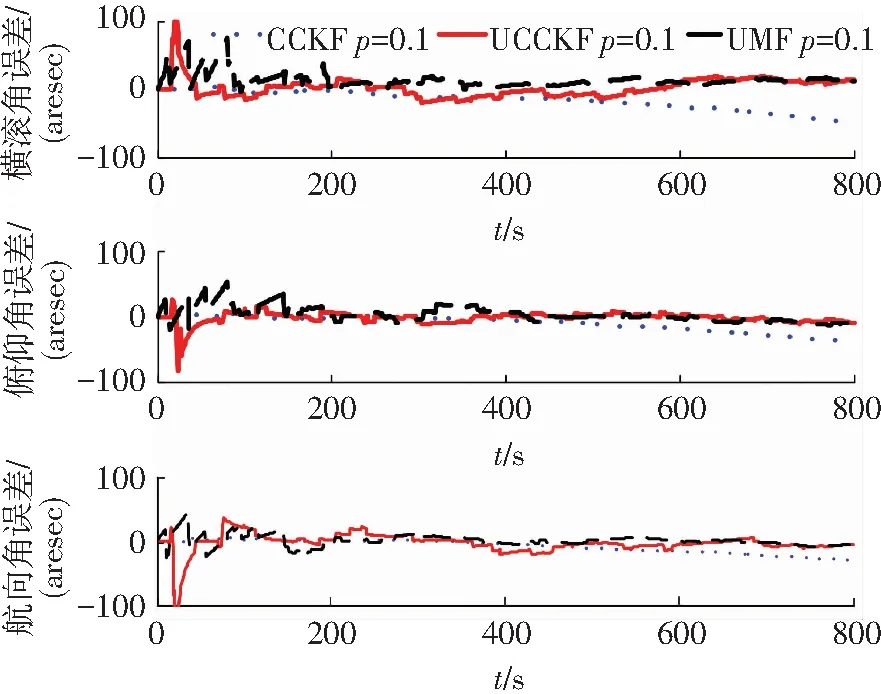
圖1 當p=0.1時姿態誤差

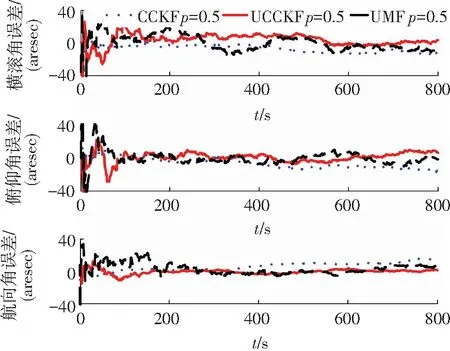
圖2 當p=0.5時姿態誤差

圖4顯示的是當星敏感器出現正確量測的概率p=0.8時3種算法的姿態角均方誤差對比圖.從圖4中可以看出，此種情況下UCCKF算法的穩態精度要高于CCKF算法和UMF算法.這是因為，相比較于CCKF算法，UCCKF算法能夠處理星敏感器量測丟失，濾波估計精度要高于CCKF算法.UMF算法雖然也能補償星敏感器量測丟失導致的模型誤差，但是它是以UKF算法為基礎，且采用強制性的四元數約束方法，對算法的精度有一定的影響，而UCCKF算法是以CKF算法為基礎，利用兩步投影理論確保滿足四元數約束條件，因此，在高維以及量測不確定的情況下，UCCKF的濾波性能更好.

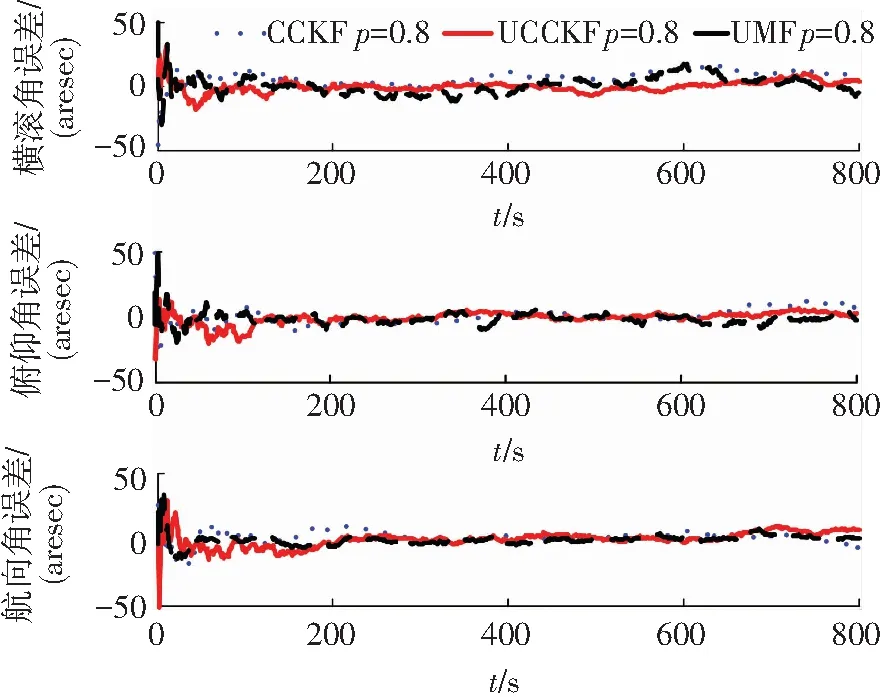
圖3 當p=0.8時姿態誤差

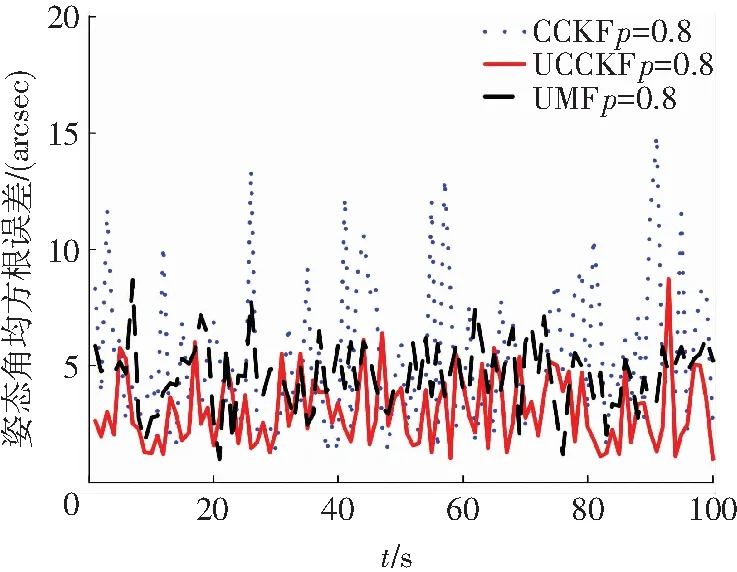
圖4 當p=0.8時姿態角均方誤差

4 結 論

1)針對星敏感器量測丟失導致的量測模型不確定問題，建立了基于不確定量測的誤差四元數非線性姿態估計模型，所建立的模型對姿態估計算法的研究提供支撐.

2)提出了一種基于不確定量測的四元數約束容積卡爾曼濾波算法，解決了上述模型中存在的四元數約束和量測不確定問題.仿真結果表明，該算法在量測不確定情況下具有更好的收斂性和更高的估計精度，驗證了算法的合理性和有效性.

[1]CHANGLubin,HUBaiqing,CHANGGuobin.Modifiedunscentedquaternionestimatorbasedonquaternionaveraging[J].JournalofGuidance,ControlandDynamics， 2013, 37(1):305-309.DOI: 10.2514/1.61723.

[2] 錢華明, 黃蔚, 孫龍. 基于改進的迭代容積卡爾曼濾波姿態估計[J]. 哈爾濱工業大學學報, 2014, 46(6): 116-122. QIAN Huaming, HUANG Wei, SUN Long. Attitude estimation based on improved iterated cubature Kalman filter[J]. Journal of Harbin Institute of Technology, 2014, 46(6): 116-122.

[3] 王碩, 宋申民, 史小平,等. 噪聲特性未知的多傳感器協方差交叉融合姿態估計[J]. 控制與決策, 2016, 31(2): 273-278. DOI: 10.13195/j.kzyjc.2014.1417. WANG Shuo, SONG Shenmin, SHI Xiaoping, et al. Multi-sensor covariance intersection fusion attitude estimation with unknown noise characteristics[J]. Control and Decision, 2016, 31(2): 273-278. DOI: 10.13195/j.kzyjc.2014.1417.

[4] QIAN Huaming, HUANG Wei, QIAN Linchen, at al. Robust extended Kalman filter for attitude estimation with multiplicative noises and unknown external disturbances[J]. IET Control Theory & Applications, 2014, 8(15): 1523-1536. DOI: 10.1049/iet-cta.2014.0293.

[5] ZANETTI R, MAJJI M, BISHOP R H, at al. Norm-constrained Kalman filtering[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(5): 1458-1465. DOI: 10.2514/1.43119.

[6] TANG Xiaojun, LIU Zhenbao, ZHANG Jiasheng. Square-root quaternion cubature Kalman filtering for spacecraft attitude estimation [J]. Acta Astronautica, 2012, 76: 84-94. DOI: 10.1016/j.actaastro.2012.02.009.

[7] LEFFERTS E J, MARKLEY F L, SHUSTER M D. Kalman filtering for spacecraft attitude estimation[J]. Journal of Guidance, Control, and Dynamics, 1982, 5(5): 417-429.DOI: 10.2514/3.56190.

[8] 喬相偉, 周衛東, 吉宇人. 用四元數狀態切換無跡卡爾曼濾波器估計的飛行器姿態[J]. 控制理論與應用, 2012, 29(1): 97-103. DOI: 10.7641/j.issn.1000-8152.2012.1.CCTA100514. QIAO Xiangwei, ZHOU Weidong, JI Yuren. Aircraft attitude estimation based on quaternion state-switching unscented Kalman filter[J]. Control Theory & Applications, 2012, 29(1): 97-103. DOI: 10.7641/j.issn.1000-8152.2012.1.CCTA100514.

[9] CRASSIDIS J L, MARKLEY F L. Unscented filtering for spacecraft attitude estimation[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(4): 536-542.DOI: 10.2514/2.5102.

[10]JULIER S J, LAVIOLA J J. On Kalman filtering with nonlinear equality constraints [J]. IEEE Transactions on Signal Processing, 2007, 55(6): 2774-2784. DOI: 10.1109/TSP.2007.893949.

[11]WANG Shuang, GENG Yunhai, JIN Rongyu. A novel error model of optical systems and an on-orbit calibration method for star sensors [J]. Sensors, 2015, 15(12):31428-31441. DOI:10.3390/s151229863.

[12]HUANG Wei, XIE Hongsheng, SHEN Chen, et al. A robust strong tracking cubature Kalman filter for spacecraft attitude estimation with quaternion constraint [J]. Acta Astronautica, 2016, 121: 153-163. DOI: 10.1016/j.actaastro.2016.01.009.

[13]NANACARA W, YAZ E E. Recursive estimator for linear and nonlinear systems with uncertain observations[J]. Signal Processing, 1997, 62(1):215-228. DOI:10.1016/S0165-1684(97)00126-6.

[14]HERMOSO-CARAZO A, LINNARES-PEREZ J. Different approaches for state filtering in nonlinear systems with uncertain observations[J]. Applied Mathematics and Computation, 2007, 187(2):708-724. DOI: 10.1016/j.amc.2006.08.083.

[15]ARASARATNAM I, HAYKIN S. Cubature Kalman filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269. DOI: 10.1109/TAC.2009.2019800.

(編輯 張 紅)

Quaternion constrained cubature Kalman filter attitude estimation based on uncertain measurements

In terms of the uncertainty measurement and the constraint on the attitude quaternion, this paper proposes a quaternion constrained cubature Kalman filter based on uncertain measurements (UCCKF) for the spacecraft attitude estimation system. The proposed filter algorithm overcomes the limitation of the quaternion-constrained cubature Kalman filter. An independent Bernoulli random process is introduced to describe the measurement uncertainty, and the three degree spherical radial cubature rule is adopted to computer the posterior mean and covariance of the system state. To deal with quaternion normalization problem, the two-step projection theory is applied to solve the quaternion constraint. Simulation results show that, compared with constrained cubature Kalman filter and unscented mixture filter, the proposed UCCKF can help to implement the better convergence and higher estimation accuracy in the case of measurement uncertainty. This illustrates that the proposed algorithm is effective and feasible for the nonlinear attitude estimation system.

attitude estimation; quaternion constraint; uncertainty measurement; cubature Kalman filter; two-step projection theory

10.11918/j.issn.0367-6234.201509022

2015-09-07

國家自然科學基金(61573113)

黃 蔚(1986—)，男，博士

黃 蔚，huangwei2393@163.com

U666.12

A

0367-6234(2017)04-0116-06

HUANG Wei

(China Ship Development and Design Center, Wuhan 430064, China)