Biot方程的完備通解在一維情況下的驗證

顏凝香 吳利華 范克

（1.江蘇省水利工程科技咨詢股份有限公司南京2100292.南京市水利規劃設計院股份有限公司南京210022）

Biot方程的完備通解在一維情況下的驗證

顏凝香1吳利華2范克2

（1.江蘇省水利工程科技咨詢股份有限公司南京2100292.南京市水利規劃設計院股份有限公司南京210022）

基于三維飽和彈性土體Biot方程的完備通解，構造了一維情況下的一組中間變量，這些變量是坐標和時間的函數，進而得到一維情況下位移和孔壓的解析解表達形式。通過給出一維算例的邊界條件求出中間變量表達式中的系數，得出位移和孔壓的最終表達式，即Biot方程的一維解答。

飽和土Biot固結完備通解理論解

1 引言

Biot（1941）在從嚴格的固結機理出發推導出能準確反映孔壓消散與土骨架變形相互關系的三維固結方程，具有重要的理論及工程應用價值。但是Biot固結方程是一組偏微分方程，在數學上求解非常困難，對于軸對稱問題和一些簡單的平面應變問題，有人推出了解析解；對于一般復雜邊界的土層情況，便無法求得解析解。河海大學王媛教授給出了三維Biot飽和土理論的完備通解。本文在直角坐標系下分別應用該通解和太沙基理論來解答土體單向固結的算例。以驗證Biot方程通解表達的實用性。Biot理論和太沙基理論的假定是基本一致的，即符合骨架線性彈性、變形微小，滲流符合達西定律等，所不同的是太沙基理論增加了土體在固結過程中法向總應力和不隨時間而變的假定，對于一維固結問題，則不存在這個問題，此時的太沙基方程和Biot固結方程是一致的。

2 通解中參數的構造

三維Biot飽和土理論的方程組為：

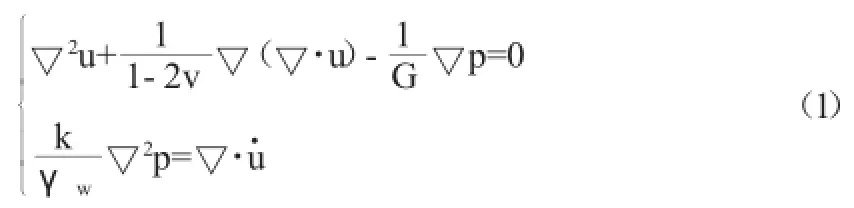
式中：u為位移，p表示孔壓，k和γw分別為土體滲透系數和水的重度。

方程組（1）有如下通解：

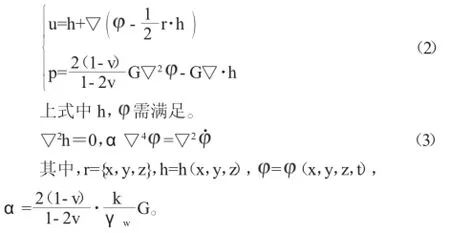
由于（2）是（1）的完備解，因此求解Biot邊值問題轉變成求出滿足方程（3）的h、，使其滿足（2）就可以了。

一維情況下，構造滿足（3）式的h，可表達為：

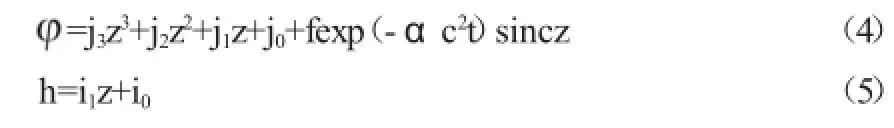
式（2）在一維情況下可寫為：

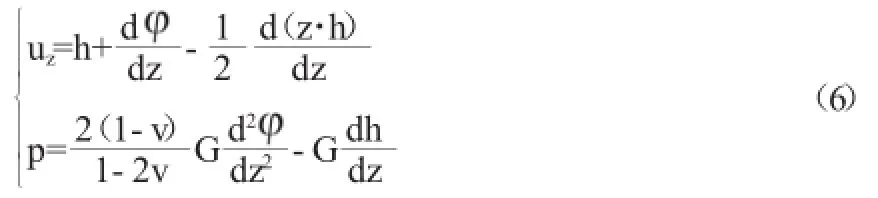
將式（4）、式（5）代入（6）得

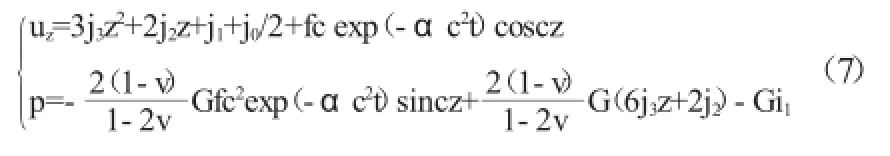
3 Biot理論一維算例解答

圖1為均質、各向同性的飽和粘土層，位于不透水的巖層上、粘土層的厚度為H，在自重應力作用下已固結穩定，僅考慮外加荷載引起的固結。若在水平地面上施加連續均布壓力，則在土層內部引起的豎向附加應力沿高度的分布將是均勻的，且等于外加均布壓力，即σz=p0。

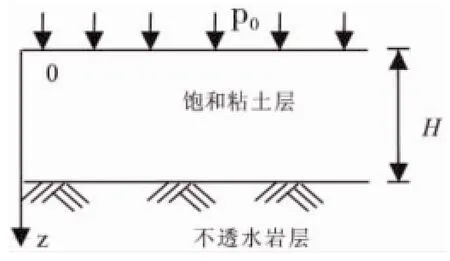
圖1 飽和粘土的一維固結圖

則有空隙水應力初始條件和邊界條件如下：

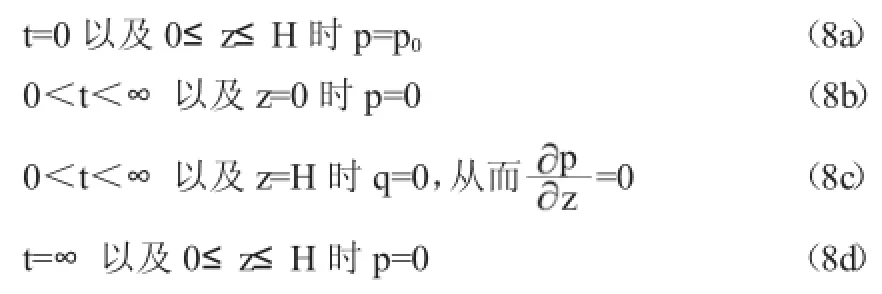
位移初始條件和邊界條件：

另外，根據有效應力原理，有以下應力條件：

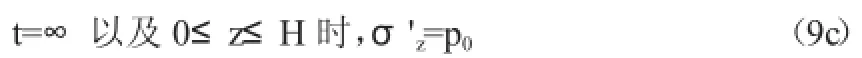
將以上式（8c）（8d）（9b）（9c）可求得

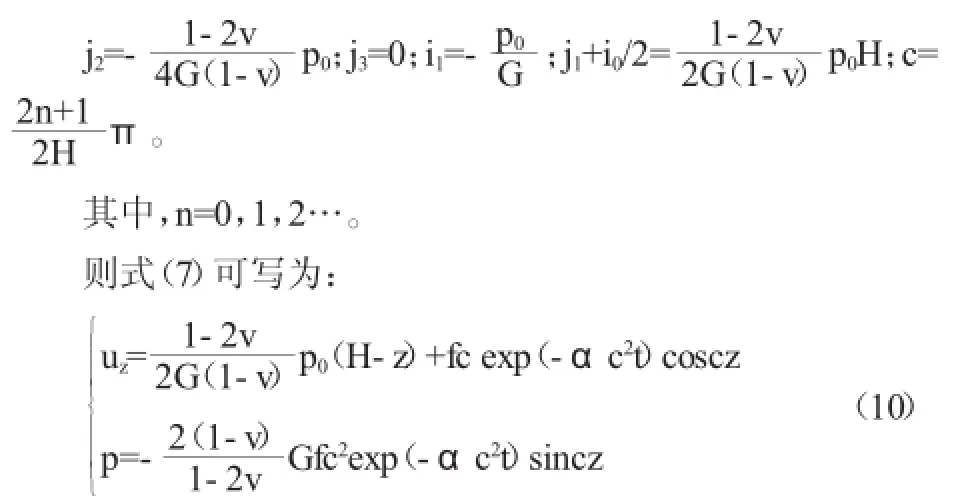
記Cn=fc，則上式中位移表達式寫為以下通式：

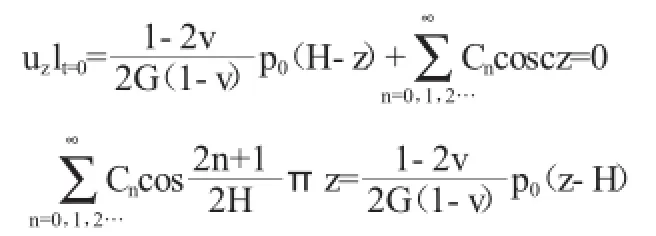
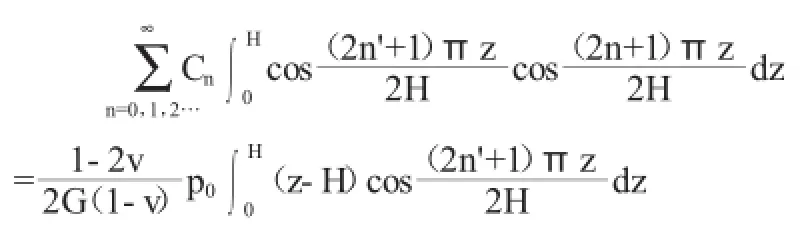
只有當n'=n時，上式左邊不為0。則有

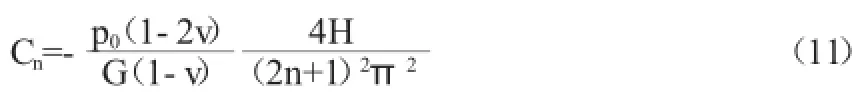
將上式代入式（10）得

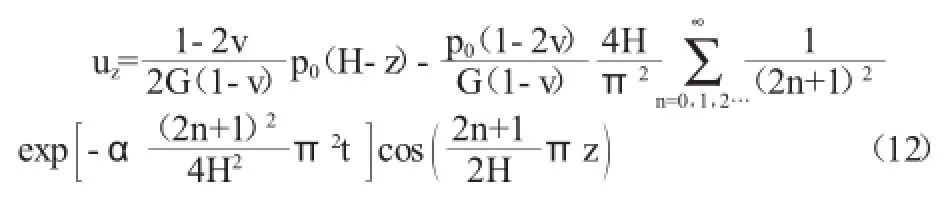
則孔壓可表達為：

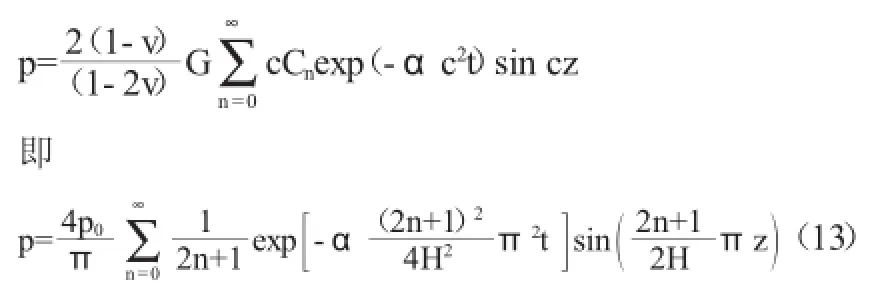
4 太沙基解答

太沙基一維固結微分方程式：

式中，Cv為固結系數。

分離變量，假定p可以表示為：

代入微分方程（14）得

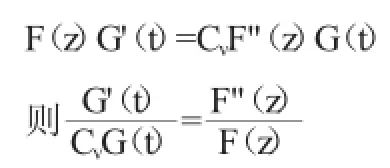
方程兩邊為不同變量的函數，只有當它們都等于常量時才有可能，令這個常量為-B2。

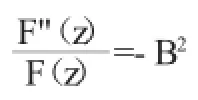
可解得F（z）=A1cosBz+A2sinBz

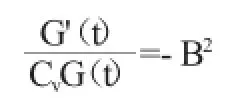
解得G（t）=A3exp（-B2Cvt）

將它們代入式（14）得

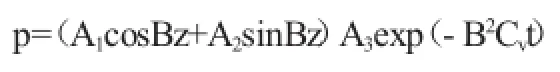
利用透水面邊界（8b）得A1=0。上式第一項消去，即

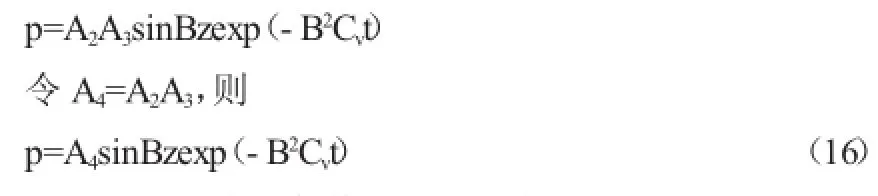
利用不透水邊界條件（8c）對上式求解：

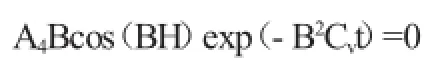
代入式（16）并寫成通式：

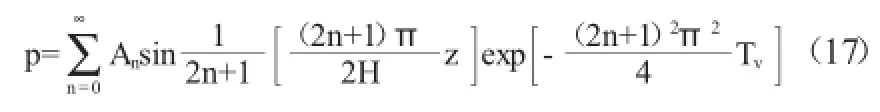
利用初始應力條件（8a）得

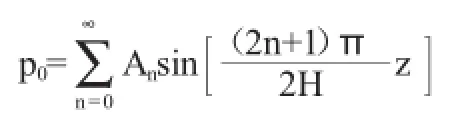
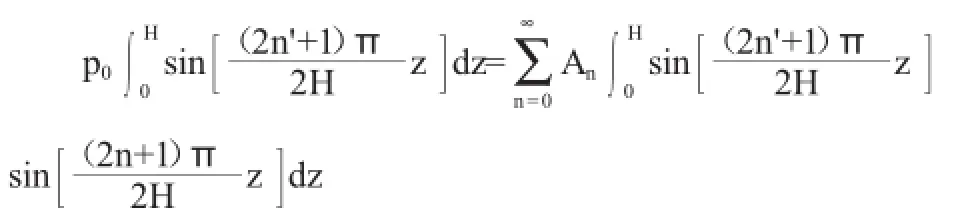
只有當n'=n時，上式左邊不為0，得

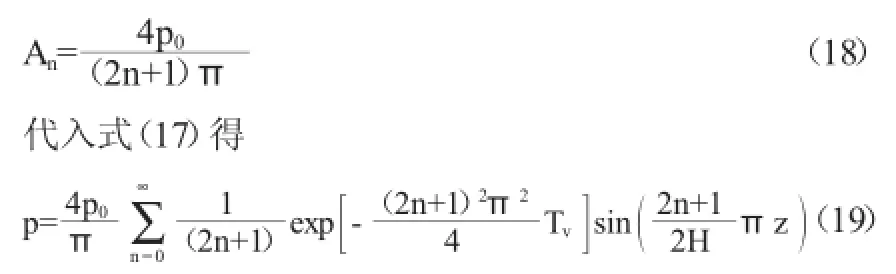
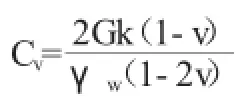
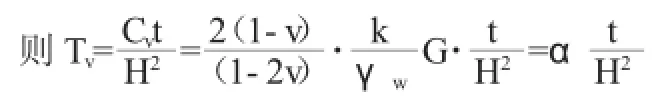
將上式代入式（19）得

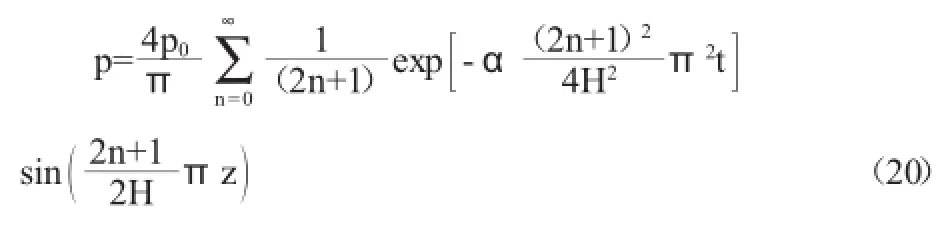
可見式（20）與Biot方程的解即式（13）是相同的。

5 結論

本文構造了直角坐標系下符合三維Biot飽和土理論通解的參量，并以此為依據得到一維固結情況下的詳細解答，同時以太沙基理論求解同一算例，結果證明兩種解答在一維情況下是一致的。驗證了Biot方程完備通解的實用性。此外，基于Biot固結理論完備通解在二維和三維情況下的應用正在研究中■