基于內涵虧值的概念格漸進式構建

吳 杰，梁 妍，馬 垣

(1.遼寧科技大學 軟件學院，遼寧 鞍山 114051； 2.遼寧科技大學 應用技術學院，遼寧 鞍山 114051)

(*通信作者電子郵箱wujieaa@163.com)

基于內涵虧值的概念格漸進式構建

吳 杰1*，梁 妍2，馬 垣1

(1.遼寧科技大學 軟件學院，遼寧 鞍山 114051； 2.遼寧科技大學 應用技術學院，遼寧 鞍山 114051)

(*通信作者電子郵箱wujieaa@163.com)

為了避免構建概念格時的繁瑣過程，提高概念格構建的效率，提出了一種基于內涵虧值通過查找頂元素來快速漸進式生成概念格的新方法。首先，形式化地定義了頂元素、舊概念、產生概念、新概念、產生子概念、內涵虧值集合、剩留父概念、超集刪除與正則隊列；提出了概念格元素是否為頂元素的判定定理并給出了其證明；其次，在原概念格的正則隊列中依次取概念元素，經超集刪除后得到剩留父概念；最后，從剩留父概念查找其所在等價類的頂元素，逐步生成新概念格的正則隊列。理論分析時間復雜度較基于屬性的漸進式概念格生成(CLIF_A)算法與FastAddIntent算法有效降低，在實驗例證對比中，概念數目大于150時，所用時間遠少于對比算法。實驗結果表明該算法方法簡單，構建效率較對比算法明顯提高。

概念格；內涵虧值；頂元素；超集刪除；正則隊列

0 引言

概念格是隸屬數學概念和概念層次結構的應用數學領域[1]。理論上結構嚴謹，能形象地體現事物之間的泛化與特化關系，在空間聚類方法、病癥智能診斷、Folksonomy、信息修復與文件瀏覽、軟件演化分析、訪問權限管理、命題集約簡等諸多領域都有著成功的應用。概念格的構建是概念格應用的前提基礎，但是一個背景中概念的個數是隨著背景的尺寸指數級增長的(比如對于半序集中反額定標尺概念的個數是2|S|)，這樣背景稍大，概念的個數就多得無法計算。如何提高概念格的構建效率是當前研究的熱點課題。

對于概念格構建的主要方法有兩大類。一類是批處理概念格生成算法[2-4]，其主要思想是先生成背景對應的全部概念，再由亞概念與超概念的連接關系，生成節點間的連線，進而完成概念格的構建；缺點是當增加對象時，需要重新構建概念格。另一類是漸進式概念格生成算法：1995年，Godin等[5]提出了概念格的漸進式生成算法，漸增式地插入新節點；2002年，謝志鵬等[6]提出了利用樹狀結構存儲節點快速構建概念格的漸進式生成算法，有效地區別節點類型，縮小了父子節點的搜查范圍；2004年，李云等[7-8]提出了基于屬性的概念格漸進式生成算法及多概念格的橫向合并算法，特別說明了屬性拆分及策略對概念格構建效率的影響；2009年，劉群等[9]提出了基于對象和屬性交叉漸進式概念格生成算法，解決了針對對象和屬性交叉漸增更新需要重新構建概念格的問題；同年，劉耀華等[10]提出了新的區間數分解與定標算法，用來處理多種類型的擴展背景，給出了相應的擴展格生成算法，改進了區間值分解與模糊概念格的屬性定標方法；2012年屈文建等[11]提出了一種利用最大秩的全1矩陣來生成概念格的算法，采用背景中最大秩全1子陣對應概念格的每個節點，通過橫向、縱向擴充成對應的子格，再經合并構建整體概念格；2013年，姚佳岷等[12]提出了一種基于概念內涵、外延升降序的雙序漸進式概念格合并算法，特點是在結構上較好地保留了原有信息；2014年，徐敏政等[13]引入元胞數據組織結構，將對象和屬性分別與概念節點的外延和內涵同時求交，提出了雙向漸進式概念格生成算法，解決了概念格構建帶來的更新問題，避免了繁瑣的合并過程；2015年，Zou等[14]通過確定概念格的順序關系和尋找更新概念，提出了一種快速生成概念格的新算法。

以上的這些漸進式概念格生成算法可以隨著增加對象(或者屬性)而動態更新概念格，適用于記錄漸增事務數據庫類型的背景，且算法的效率都有不同程度的提高，但是，當構建概念格的概念數目巨大時，為避免構建時的復雜過程，有效地提高構建的效率，本文提出了一種基于內涵虧值，經由超集刪除，通過剩留父概念查找其所在等價類的頂元素來生成概念格正則隊列的全新方法，理論分析與實驗對比論證均表明該漸增式構建算法是可行的，不僅方法簡單有效，且在時間性能上比其他方法優越，構建效率更高。

1 概念格的定義及定理

定義1[15]若U為對象的集合，M為屬性的集合，I?U×M為U和M之間的關系，稱三元組=(U,M,I)為形式背景，簡稱背景。

定義2[15]若=(U,M,I)為一個背景，A?U，B?M，

f(A)={m∈M|?u∈A,(u,m)∈I}

g(B)={u∈U|?m∈B,(u,m)∈I}

若f(A)=B，g(B)=A，稱二元組(A,B)為形式概念，簡稱概念。并稱A為概念(A,B)的外延，B為概念(A,B)的內涵。上所有概念的集合記為B()。

性質1[15]若=(U,M,I)為一個背景，A1,A2?U，B1,B2?M，則：

1)A1?A2?f(A2)?f(A1)；

2)A1?A2?g(A2)?g(A1)；

3)A1?g(f(A1))；

4)B1?f(g(B1))；

5)f(A1)=f(g(f(A1)))；

6)g(B1)=g(f(g(B1)))；

7)f(A1)∩f(A2)=f(A1∪A2)；

8)g(B1)∩g(B2)=g(B1∪B2)。

定義3[15]設=(U,M,I)為一個背景，(X1,Y1)，(X2,Y2)∈B()：

1)若X1?X2，稱(X1,Y1)為(X2,Y2)的子概念，(X2,Y2)為(X1,Y1)的父概念，記為(X1,Y1)≤(X2,Y2)。若X1?X2，記為(X1,Y1)<(X2,Y2)。

2)若(X1,Y1)<(X2,Y2)，且不存在(X3,Y3)，有(X1,Y1)<(X3,Y3)<(X2,Y2)，則稱(X1,Y1)為(X2,Y2)的直接子概念，(X2,Y2)為(X1,Y1)的直接父概念，記作(X1,Y1)(X2,Y2)，并稱Y2-Y1為(X1,Y1)的一個內涵虧值。

定義4[15]設(M,≤)是一個半序集，若M中任何兩個元素都有上確界和下確界,則稱(M,≤)為一個格。

表1 在0的基礎上增加對象u=6后得到的背景1

Tab.1 Formal context 1 formed by adding u=6 to original context 0

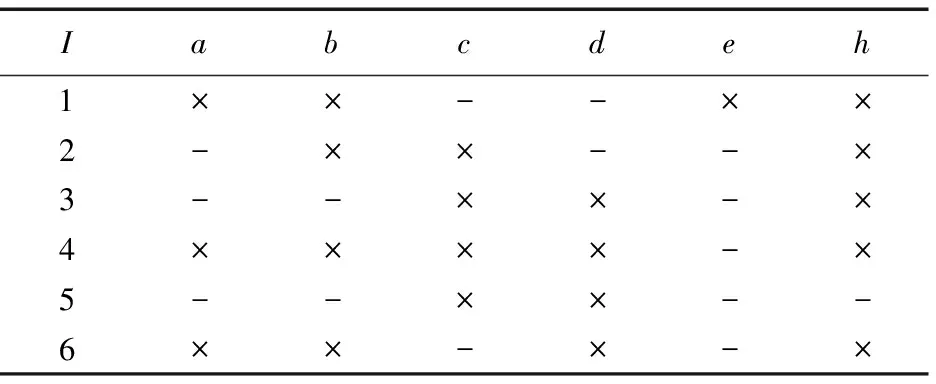
表1 在0的基礎上增加對象u=6后得到的背景1

Iabcdeh1××--××2-××--×3--××-×4××××-×5--××--6××-×-×

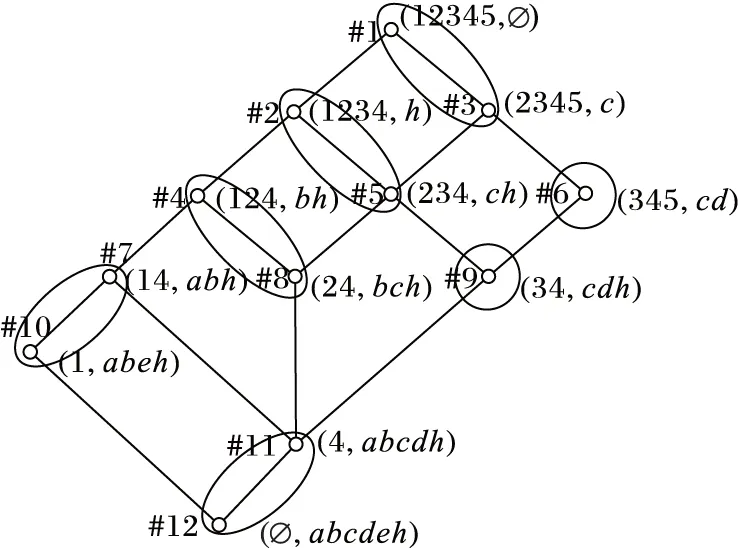
圖1 B=abdh在概念格(0)中形成的等價類

圖(0)的頂元素子格

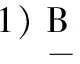
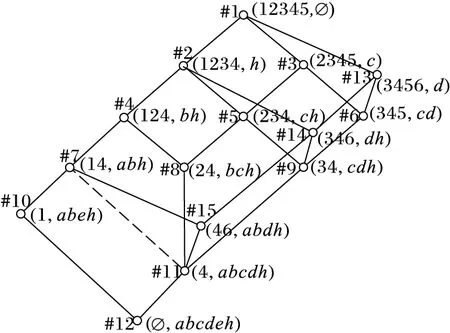
圖3 背景1的概念格

2 內涵虧值

定義6 將概念及其內涵虧值表示成(#t,X,Y,W)，其中：X為外延；Y為內涵；#t中的t為自然數，是生成概念時依次賦予的概念號；W={#t1:S1,…,#tk:Sk}為(X,Y)的內涵虧值集合，其中#ti:Si表示#ti概念為(X,Y)的一個直接父概念，Si(i=1,2,…,k)表示#ti對(X,Y)的內涵虧值。

定理1 若(X,Y)的內涵虧值集合為Δ(X,Y)={S1,S2,…,Sk}，且S1∩B,S2∩B,…,Sk∩B都不空，則(X,Y)是頂元素；若存在某個Si∩B=?，則(X,Y)不是頂元素，且與Si對應的直接父概念屬于同一個等價類。

證明 若(X,Y)是頂元素，則它的任意一個直接父概念(Xi,Yi)，有Y∩B?Yi∩B，所以對于內涵虧值Si=Y-Yi，必有Si∩B=(Y-Yi)∩B=(Y∩B)-(Yi∩B)≠?，反之若Si∩B=?，則Si對應的直接父概念(Xi,Yi)，必有(Y-Yi)∩B=?，即Y∩B=Yi∩B，所以(X,Y)不是頂元素，且與Si對應的直接父概念屬于同一個等價類。

定義7 將概念排成正則隊列，所謂正則隊列，即在這個隊列中任何父概念都不出現在其子概念的后面。

3)若其內涵虧值集合W中所有虧值與B的交都不為?，且YB，則在(1)中有新概念(#n,X∪{u},Y∩B,W1)及產生子概念(#t,X,Y,W2)。其中：W1={#p:(Y∩B)-Y1|(#p,X1,Y1,Wp)是(X,Y)在頂元素格的直接父概念產生的概念}；W2=W∪{#n:Y-B}，Y-B=Y-(Y∩B)是新概念(#n,X∪{u},Y∩B,W1)對(X,Y)的內涵虧值，其中W中要刪除同樣是新概念(#n,X∪{u},Y∩B,W1)的直接父概念產生的內涵虧值。

為了求新概念(X∪{u},Y∩B)的內涵虧值，需求出(X,Y)在頂元素格中的各個直接父概念。為此有：

證明 因為頂元素(X,Y)與(X1,Y1)分別為等價類[(X,Y)]θ與[(X1,Y1)]θ的最大元素，所以有Y=f(g(Y∩B))，Y1=f(g(Y1∩B))。又因為在頂元素格中(X1,Y1)為(X,Y)的直接父概念，所以有Y1∩B?Y∩B，于是f(g(Y1∩B))?f(g(Y∩B))，即Y1?Y。然而Y1∩B?Y∩B，有Y1≠Y，所以Y1?Y，即(X1,Y1)也是(X,Y)的父概念，于是必有一個(X,Y)的直接父概念(X2,Y2)滿足Y1?Y2?Y，有Y1∩B?Y2∩B?Y∩B，但因為(X1,Y1)在頂元素子格中是(X,Y)的直接父概念，所以有Y2∩B=Y1∩B或者Y2∩B=Y∩B。由于(X,Y)也是頂元素，有Y2∩B≠Y∩B，所以Y2∩B=Y1∩B。

為了方便地鑒別(X,Y)的哪些直接父概念所在等價類的頂元素為(X,Y)在頂元素格中的直接父概念，給出如下形式化的定義。

定義8 若概念(X,Y)的虧值集合為W，B?M：

1)若W=?(最大概念的情況)，則W相對于B的超集刪除為?。

2)若W={S1,S2,…,SK}，在集合{Si∩B,Si+1∩B,…,SK∩B}中將是其他元素的超集刪除，相同的值只留一個。

稱其結果為W相對于B的超集刪除，簡稱為超集刪除。稱這些未被刪除的內涵虧值對應的直接父概念為(X,Y)的剩留父概念。

顯然剩留父概念所在等價類的頂元素為(X,Y)在頂元素格中的直接父概念。

例3 如圖1所示，#11概念的內涵虧值集合為Δ(4,abcdh)={cd,ad,ab}，這些內涵虧值與B=abdh的交分別為cd∩abdh=d，ad∩abdh=ad，ab∩abdh=ab，將是其他元素超集的刪除，剩下d及ab。d及ab所對應的內涵虧值為cd及ab，cd及ab所對應的直接父概念#7及#9為剩留父概念，它們所在等價類的頂元素為#11概念在頂元素格中的直接父概念。又如圖1所示，#9概念的內涵虧值集合為Δ(34,cdh)={#5:d,#6:h}，這些內涵虧值與B=abdh的交分別為d∩abdh=d，h∩abdh=h，超集刪除后還為d及h，d及h所對應的直接父概念是#5概念及#6概念，它們為剩留父概念。#6概念所在等價類的頂元素就是本身，#5概念所在等價類的頂元素為#2概念，由此#2概念及#6概念為#9概念在頂元素格中的直接父概念。

利用剩留父概念查找其所在等價類的頂元素方法如下。

由定理1，檢查它的各個內涵虧值Si與B的交是否為?，都不為?，則為頂元素。若存在某個Si∩B=?，則Si對應的直接父概念(Xi,Yi)與(X,Y)在同一個等價類中。于是對(Xi,Yi)做如上的檢查，直到存在某一個概念，其內涵虧值與B的交都不為空為止，此時這個概念就是(X,Y)直接父概念所在等價類的頂元素。若某個內涵虧值Si，有Si∩B=?，則任何一個內涵虧值Sj∩B都為它的超集，于是超集刪除的結果一定是{#i:?}。所以是否存在某個Si∩B=?，可用超集刪除的結果是否為{#i:?}來判定。

#9概念內涵虧值集合中的d對應的直接父概念是#5概念，由于是正則隊列，所以#5概念已出現在L1中，又由于#5概念的內涵虧值集合為Δ(234,ch)={#2:c,#3:h}，超集刪除得{#2:?}，所以在L1中繼續向上找#2概念，#2概念的內涵虧值集合為Δ(1234,h)={#1:h}，超集刪除得{#1:h}，不是{#i:?}，所以#2概念為#14概念(346,dh)的一個直接父概念，且內涵虧值為：Si∩B=d∩abdh=d。

#9概念內涵虧值集合中的h對應的直接父概念是#6概念，由于是正則隊列，所以#6概念已出現在L1中，又由于#6概念的內涵虧值集合為Δ(345,cd)={#3:d,#13:c}，超集刪除得{#13:?}，所以在L1中繼續向上找#13概念，#13概念的內涵虧值集合為Δ(3456,d)={#1:d}，超集刪除得{#1:d}，不是{#i:?}，所以#13概念為#14概念的一個直接父概念，且內涵虧值為：Si∩B=h∩abdh=h。

即#14概念在L1中的直接父概念有兩個，#2概念及#13概念，且內涵虧值分別為：d及h。

3 概念格構建算法

1)內涵虧值集合的超集刪除子程序CO(W)。

輸入：W={#t1:S1,…,#tk:Sk}(允許W=?)。其中，#ti:Si表示Si為相對于概念#ti的內涵虧值。 輸出：{#tp:Sp∩B,…,#tq:Sq∩B}(允許是?)。

方法：

IfW= ? Then 輸出?，結束 ElseFori= 1 tokForj= 1 tokIfi≠j,Si∩B?Sj∩B且#ti:Si未作刪除標記 Then #ti:Si作刪除標記 //因為是?，不是?，所以最終相同值只留一個 Exit(j)

//退出j循環 EndIf

Next(j)

Next(i)

輸出{#t:S∩B|#t:S未作刪除標記}，結束

EndIf

2)查找#t概念所在等價類頂元素的子程序Top(#t,V)。

輸入：#t,V。其中，#t為概念的概念號，#V為概念的內涵虧值集合。 輸出：#i，為#t所在等價類頂元素的概念號。

方法：

//再向上查找Else輸出#t，結束 //#t為頂元素，輸出#tEndIf

EndIf

3)添加新對象后的概念格及內涵虧值的計算ADD(L,u,B,n)。

L1:=?

Foreach(#t,X,Y,W) inLby order doWB:=CO(W)

//WB中存放W超集刪除的結果IfWB僅有一個元素 #i:?Then(#t,X,Y,W)送入L1隊尾

//#t不為頂元素，直接送入L1ElseIfY?BThen(#t,X∪{u},Y,W)送入L1隊尾 //#t為頂元素，且Y?B，則外延加u后送L1ElseW1:=?IfBW≠?ThenForeach(#i:Si∩B)inWB 在L1中取概念號為#i的概念(#i,C,D,V) 令W1:=W1∪{Top(#i,V):Si∩B}Next

EndIf

n:=n+1

(#n,X∪{u},Y∩B,W1)送入L1隊尾

W2:={#i:Si|(#i:Si)∈W且#i未出現在W1中}

W2:=W2∪{#n:(Y-B)}

(#t,X,Y,W2)送L1隊尾

EndIf

EndIf

Next

輸出L1結束。

L:=(#1,?,M,?)

//L為只有一個元素(#1,?,M,?)的隊列n:=1For each (u,B) inADD(L,u,B,n)L:=L1Next

輸出L，結束。

在硬件配置為CPUInteli3 2.40GHz，內存為8GB，在VisualStudio2010的環境下，用VB.Net語言實現本文提出的概念格構建算法，與文獻[14]和文獻[7]算法進行了比較，隨機生成20個形式背景，概念個數從50開始遞增到500，變化基數為50，實驗結果如圖4所示，當概念的數目小于100時，三種算法的區別并不明顯，當概念的數目逐漸變大(大于150)時，本文提出的概念格構建算法的運行時間更快，效果更優越，證明了其算法的有效性。

4 結語

本文提出了一種基于內涵虧值快速構建概念格的新方法：

1)將原概念格排成正則隊列后依次取概念元素。

2)所取概念的內涵虧值集合作超集刪除。

3)由定理1判定，若為頂元素且元素內涵不是B的子集，則得到產生子概念與新概念；若為頂元素且元素內涵是B的子集，則得到產生概念。

4)由定理1判定，若不為頂元素，經由剩留父概念繼續向上查找，查找其所在等價類的頂元素，逐步生成新概念格的正則隊列。

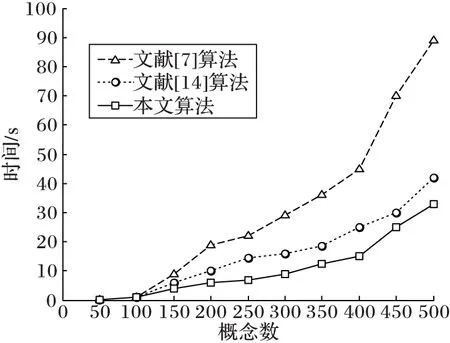
圖4 三種算法運行時間對比

同時給出了概念格構建的算法。三種算法實驗結果的對比，表明本文提出的方法顯著提高了構建概念格的效率，為數據挖掘進一步的應用研究創造了良好的條件。

對于文章提出的方法，可以給出一些技巧使步驟簡化，是進一步研究的方向。

)

[1]WILLER.Restructuringlatticetheory:anapproachbasedonhierarchiesofconcepts[C]//ICFCA’ 09:Proceedingsofthe7thInternationalConferenceonFormalConceptAnalysis.Berlin:Springer, 2009: 445-470.

[2]LINDIGC.Fastconceptanalysis[M]//WorkingwithConceptualStructuresContributionstoICCS2000.Aachen,Germany:ShakerVerlag, 2000: 152-161.

[3]STUMMEG,TAOUILR,BASTIDEY,etal.Fastcomputationofconceptlatticesusingdataminingtechniques[C]//Proceedingsofthe7thInternationalWorkshoponKnowledgeRepresentationMeetsDatabases.[S.l.]:VLDBEndowment, 2010: 129-139.

[4] 陳震,張娜,王甦菁.一種基于概念矩陣的概念格生成算法[J].計算機科學,2010,37(9):180-183.(CHENZ,ZHANGN,WANGSJ.Newalgorithmofgeneratingconceptlatticebasedonconcept-matrix[J].ComputerScience, 2010, 37(9): 180-183.)

[5]GODINR,MISSAOUI,R,ALAOUIH.IncrementalconceptformationalgorithmbasedonGalois(concept)lattices[J].ComputationalIntelligence, 1995, 11(2):246-267.

[6] 謝志鵬,劉宗田.概念格的快速漸進式構造算法[J]．計算機學報，2002，25(5):490-496.(XIEZP,LIUZT.Afastincrementalalgorithmforbuildingconceptlattice[J].ChineseJournalofComputers, 2002, 25(5): 490-496.)

[7] 李云,劉宗田,沈夏炯,等.基于屬性的概念格漸進式生成算法[J].小型微型計算機系統,2004,25(10):1768-1771.(LIY,LIUZT,SHENXJ,etal.Attribute-basedincrementalformationalgorithmofconceptlattice[J].JournalofChineseComputerSystems, 2004, 25(10): 1768-1771.)

[8] 李云,劉宗田,徐曉華,等.多概念格的橫向合并算法[J].電子學報,2004,32(11):1849-1854.(LIY,LIUZT,XUXH,etal.Horizontalunionalgorithmofmultipleconceptlattices[J].ActaElectronicaSinica, 2004, 32(11): 1849-1854.)

[9] 劉群,冷平,孫凌宇.基于對象和屬性交叉的漸進式概念格生成算法[J].計算機工程,2009,35(7):59-60.(LIUQ,LENGP,SUNLY.Incrementalconceptlatticeformationalgorithmbasedonalternateobjectandattribute[J].ComputerEngineering, 2009, 35(7): 59-60.)

[10] 劉耀華,周文,劉宗田.一種區間數分解與定標算法及其擴展形式背景的概念格生成方法[J].計算機科學,2009,36(10):213-216.(LIUYH,ZHOUW,LIUZT.Intervalscalingalgorithmanditsconceptlatticeconstructionfromextendedformalcontext[J].ComputerScience, 2010, 37(9): 180-183.)

[11] 屈文建,譚光興,邱桃榮.運用全1矩陣的概念格生成算法[J].小型微型計算機系統,2012,33(3):558-564.(QUWJ,TANGX,QIUTR.Newalgorithmofgeneratingconceptlatticeusinguniversalmatrix[J].JournalofChineseComputerSystems, 2012, 33(3): 558-564.)

[12] 姚佳岷,楊思春,李心磊,等.雙序漸進式概念格合并算法[J].計算機應用研究,2013,30(4):1038-1040.(YAOJM,YANGSC,LIXL,etal.Incrementaldoublesequencealgorithmofconceptlatticeunion[J].ApplicationResearchofComputers, 2013, 30(4): 1038-1040.)

[13] 徐敏政,何宗宜,劉亞虹,等.雙向漸進式概念格生成算法[J].小型微型計算機系統,2014,35(1):172-176.(XUMZ,HEZY,LIUYH,etal.Bidirectionalincrementalformationalgorithmofconceptlattice[J].JournalofChineseComputerSystems, 2014, 35(1): 172-176.)

[14]ZOULG,ZHANGZP,LONGJ,etal.Afastincrementalalgorithmforconstructingconceptlattices[J].ExpertSystemswithApplications, 2015,42(9): 4474-4481.

[15] 馬垣,曾子維,遲呈英,等.形式概念分析及其新進展[M].北京:科學出版社,2011:11-31.(MAY,ZENGZW,CHICY,etal.FormalConceptandit’sNewProgress[M].Beijing:SciencePress, 2011: 11-31.)

[16] 梁妍,吳杰,馬垣,等.基于概念格虧值的共軛對方法研究[J].計算機工程與設計,2014,35(1):171-176.(LIANGY,WUJ,MAY,etal.Researchonmethodofconjugatepairsbasedonwanedvaluesfromconceptlattice[J].ComputerEngineeringandDesign, 2014, 35(1): 171-176.)

ThisworkispartiallysupportedbytheNationalNaturalScienceFoundationofChina(61273019),theYouthFundofUniversityofScienceandTechnologyLiaoning(2014QN21).

WU Jie, born in 1981, Ph.D.candidate, lecturer.His research interests include database and data mining, formal concept analysis.

LIANG Yan, born in 1982, M.S., lecturer.Her research interests include database and data mining, formal concept analysis.

MA Yuan, born in 1941, Ph.D., professor.His research interests include database and data mining, formal concept analysis.

Incremental formation of concept lattice based on intent waned value

WU Jie1*, LIANG Yan2, MA Yuan1

(1.SchoolofSoftware,UniversityofScienceandTechnologyLiaoning,AnshanLiaoning114051,China;2.SchoolofAppliedTechnology,UniversityofScienceandTechnologyLiaoning,AnshanLiaoning114051,China)

Concerning the tedious process during the construction of concept lattice, to improve the efficiency of building concept lattices, a new incremental method of constructing concept lattice based on intent waned value by seeking top elements was proposed.Firstly, top element, original concept, produced concept, new concept, producer concept, the set of intent waned values, reminded parent concept, superset delete and regular queue were formally defined; the judging theorem and proof whether the concept elements were top elements were given.Secondly, the elements were extracted from the regular queue of the original lattice in due order and the reminded parent concepts were got after superset delete.Finally, the top elements were found from the equivalent classes of the reminded parent concepts and the regular queue of the new lattice was gradually generated.Time complexity was effectively reduced compared with the Attribute-based Concept Lattice Incremental Formation (CLIF-A) algorithm and the FastAddIntent algorithm by theory analysis.In comparison with simulated experiments, the time consumption of the proposed algorithm was far less than the comparative approaches in large size of population.The simulation results show that the proposed algorithm is simple, and can effectively improve the time performance, meanwhile provides better performance in construction efficiency.

concept lattice; intent waned value; top element; superset delete; regular queue

2016-06-14;

2016-08-22。

國家自然科學基金資助項目(61273019)；遼寧科技大學青年基金資助項目(2014QN21)。

吳杰(1981—)，男，山東蓬萊人，講師，博士研究生，主要研究方向：數據庫與數據挖掘、形式概念分析； 梁妍(1982—)，女，遼寧鞍山人，講師，碩士，主要研究方向：數據庫與數據挖掘、形式概念分析； 馬垣(1941—)，男，北京人，教授，博士，主要研究方向：數據庫與數據挖掘、形式概念分析。

1001-9081(2017)01-0222-06

10.11772/j.issn.1001-9081.2017.01.0222

TP18

A