博弈論在預防化工園區事故多米諾效應中的應用*

昌偉偉，吳　兵

(中國礦業大學(北京) 資源與安全工程學院， 北京 100083)

0　引言

經過幾十年的發展，我國已經形成了規模龐大、門類齊全和配置完善的化學工業體系，化工園區作為化學工業體系的重要組成部分，對我國化學工業的發展起到了舉足輕重的作用。據中國石油和化學工業聯合會化工園區工作委員會所做的一次全國性調研統計，截至2015年底，全國重點化工園區或以石油和化工為主導產業的工業園區共有502家，其中，國家級化工園區(包括經濟技術開發區、高新區)47家，省級化工園區262家，地市級化工園區193家[1]。由于化工園區內存在種類繁多的化學工藝過程和工藝設備，一旦發生事故，后果不堪設想。2010年，大連孤山化工園區“7·16”輸油管道爆炸事故，若不是及時關閉輸油管道臨近的儲油罐，勢必引發整個園區危險化學品事故的多米諾效應。2016年，天津港“8·12”特大火災爆炸事故，亦是由于危險品倉庫首先爆炸而引發園區危險化學品事故多米諾效應，現場形成6處大火點及數10處小火點，事故最后造成165人遇難，8人失蹤，798人受傷，304幢建筑物、12 428輛商品汽車、7 533個集裝箱受損[2-3]，是近年來我國最大的化學品爆炸事故。如此突出的安全風險，對于化工園區的安全發展和政府的安全監管都帶來了極大的挑戰。

化工園區內重大事故具有多米諾效應，當園區內某單元(企業)發生的事故能量足夠大時，其危害便會涉及園區內其他單元，導致多米諾效應。從事故發生的能量角度，應用爆炸學、傳熱學、網絡理論等知識，可以找出重大事故發生時能量傳播的途徑，結合園區內各單元現有的風險應對措施，切斷事故的多米諾效應[4]。從經濟角度，園區內各單位必然從自身利益出發，選擇最經濟的方式避免事故多米諾效應對自身企業產生不良影響。無論從何角度出發，預防多米諾效應的有效手段便為園區內各單元間相互合作[5]。

本文應用博弈論理論，從經濟角度分析化工園區內各單元為了預防重大事故的多米諾效應，彼此間的博弈過程，最終求解出均衡點，以期為預防化工園區事故多米諾效應提供理論參考。

園區內各單元的安全投入主要包括用于提升企業安全管理水平和預防事故發生的人員、設備、材料、改善作業環境和管理水平等方面的資金投入，其中，政府強制要求配置的各種人材機等費用為安全投入的下限，各單元為進一步提升安全水平而進行的投入，可以更有效地預防事故，同時可以減少自身發生事故與相鄰單元發生事故造成本單元的損失。在本文中認為企業高于政府要求部分的安全投入可以有效的預防事故多米諾效應。

博弈論又稱對策論，可以定義為是對智能的理性決策者之間沖突與合作的數學模型的研究，博弈論為分析那些涉及兩個或更多參與者且其決策會影響互相間的利益的局勢提供了1種數學方法[6，7]。最初應用于經濟學范疇，后廣泛應用于軍事、工程等學科。在安全領域，Nadeau[8]應用博弈論分析不同社會成員間對于職業健康和安全目標的策略選擇，通過建立博弈均衡點，找出不同社會成員的最佳安全策略；Reniers[9]應用博弈論討論多企業間協同安全管理的策略選擇問題，對于同一個安全目標，不同企業有不同的策略選擇，通過博弈分析，確定適合不同企業的最佳策略；宗翔等[10]采用博弈論原理分析隧道與地下工程的風險，將大自然與施工方作為博弈雙方，通過技術參數分析提出應對地下工程風險的措施；李路等[11]將博弈論應用于電網事故的應急處理中，分析電網事故與調度之間的博弈關系，確定最佳的調度措施。采用博弈論對化工園區事故多米諾效應進行研究，提高各單位間的合作意愿，使園區內各單元選擇最佳安全投入策略，避免產生重大事故的發生，對化工園區的安全管理將會產生積極的影響。

1　博弈模型建立

1.1　問題的提出

在化工園區內存在生產不同類型化工產品的企業(本文稱之為單元)，各單元是構成化工園區的基本元素，各單元不僅面臨本單元內部發生事故對自身產生的損失，同時，也會面臨園區內鄰近單元發生事故對其產生的影響，這種由相鄰單元發生事故造成本單元事故損失的現象，稱之為多米諾效應。由于多米諾效應的影響，各單元不僅要面臨本單元發生事故造成損失(本文稱之為直接損失)的風險，也面臨相鄰單元發生事故造成本單位損失(本文稱之為間接損失)的風險，因此各單元的安全投入既包括為了提升自身安全管理和預防事故水平的安全投入，又包括為了預防相鄰單元事故多米諾效應的安全投入。由于各單元利益出發點不同，為預防多米諾效應進行安全投入的動力也不同，則會出現個別單元愿意為了預防多米諾效應進行安全投入，而個別單元不愿意為預防多米諾效應進行安全投入的情況，彼此間的博弈由此產生[12-14]。

1.2　條件假設

假設化工園區由n個基本單元(化工企業)構成，每個單元均為理性的個體，對博弈參數進行定義如下：

1)將是否愿意為預防多米諾效應進行安全投入作為各單元的基本策略Ai，進行安全投入為I，不進行安全投入為NI，則Ai={I，NI}。

2)將單元i不進行安全投入發生事故造成單元i自身的損失定義為Li≥0，其發生概率為0≤Pii≤1。

3)將單元j不進行安全投入發生事故造成相鄰單元i的損失定義為Lj≥0，j≠i，其發生概率為0≤Pji≤1。

4)將單元i的為了預防多米諾效應的安全投入定義為ci≥0。

5)定義Ψ為當單元i選擇任意策略Ai時，園區內采取策略I的單元數量，Φ為園區內采取策略NI的單元數量。

6)定義li({Ψ},Ai)為當單元i選擇選擇任一策略時，單元i的間接損失。

7)定義ui(i=1,…,n)為單元i無論選擇何種策略，其安全投入與事故損失之和。

基于以上的假設與參數定義，可以得出當單元i選擇策略Ai=I時，其面臨的支付值為：

ui=ci+li({Ψ},I)

(1)

當單元i選擇策略Ai=NI時，其面臨的支付值為：

ui=LiPii∏(1-Pji)+li({Ψ},NI)(1-Pii)(j≠i，j∈Φ)

(2)

公式(2)的前半部分表示單元i的直接損失，后半部分表示單元i的間接損失。通過各參與方不同策略選擇模型的建立，可以進一步分析博弈模型的納什平衡條件和化工園區內各單元間的合作是否處于博弈穩定的情形。

1.3　支付矩陣建立

為了進一步分析，假設1.2節建立的博弈模型參與方僅為2個單元，即單元1和單元2，則可以建立2個單元的支付矩陣，見表1。

表1　化工園區內2單元的支付矩陣

假設企業為預防多米諾效應進行的安全投入對于預防化工園區重大事故多米諾效應的是可靠并有效的，根據支付矩陣，會出現4種情況：

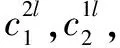
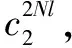
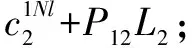
4)當各單元均選擇策略NI時，各單元的支付值為自身發生重大事故的損失與對方發生重大事故對其的影響值之和，即單元1的支付值為P11L1(1-P21)+P21L1(1-P11)，單元2的支付值為P21L2(1-P12)+P12L2(1-P22)。

2　均衡分析

理性個體如何選擇策略與博弈模型內的參數有關，不同的參數關系會產生不同的納什均衡點。針對表1建立的支付矩陣進行分析，可以得出不同條件下的納什均衡點，見表2。

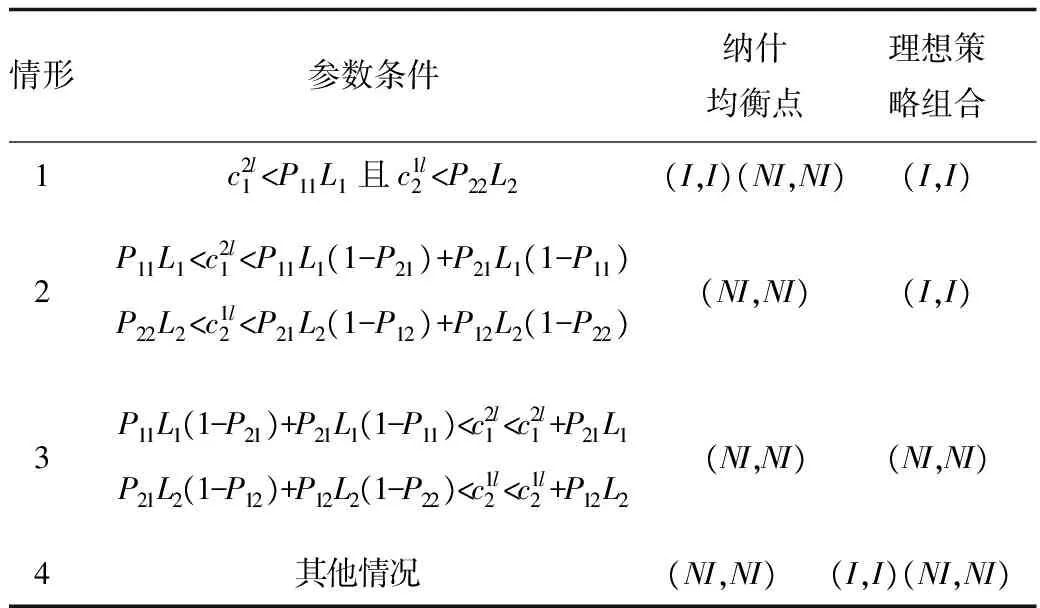
表2　不同參數條件下的納什均衡點

2.1　情形1

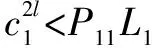
2.2　情形2

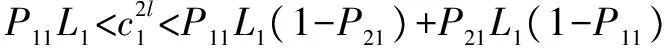
2.3　情形3

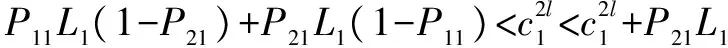
2.4　情形4

當2個博弈單元中的1個單元選擇進行合作策略(I，I)的支付值大于選擇不進行合作的支付值時，必然會選擇代價最小的策略組合，(NI，NI)將會是穩定的納什均衡點。

這種情形需對各單元進行認真仔細的分析，分析當采取合作策略時安全投入的支付值與安全生產達到的水平之間的關系，根據具體情況選擇是否采取措施促使各單元選擇策略(I，I)。

3　實例分析

選擇某LPG園區的數據進行實例分析，園區內存在單元1和單元2，單元1包括12個LPG儲罐；單元2包括7個LPG儲罐。相鄰2個單元同時面臨著由于自身發生事故造成的損失和相鄰單元事故多米諾效應而造成的損失。

3.1　參數選擇

Pii為由于單元內部發生事故造成本單元損失的發生概率，對于本案例取P11為1.10×10-4，P22為0.64×10-4。

Pij為由于單元內部發生事故造成相鄰單元損失的發生概率，對于本案例取P12為5.50×10-4，P21為4.34×10-4。

事故損失Li是通過發生事故后用于重建或修復生產單元發生的費用來確定。對于單元1潛在的由于多米諾效應造成的損失值L1=68 777 800元，單元2潛在的由于多米諾效應造成的損失值L2=14 068 186元。

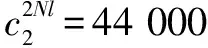
3.2　博弈分析

將數據代入表1，可以得到該LPG園區的支付矩陣，見表3。

表3　LPG園區內兩單元支付矩陣

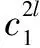
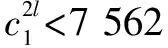
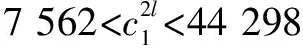
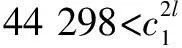
4)當處于情形4時，由于各單元選擇合作策略(I，I)時的支付值要大于至少有1個單元選擇不合作的支付值，那么對于管理者，盡量選擇對1個單元或者全部單元采取激勵措施，使雙方均選擇策略(I，I)。

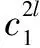
4　結論

1)建立了化工園區內各單元為了預防事故多米諾效應的博弈模型。博弈模型考慮了各單元自身發生事故的概率與損失，相鄰單元發生事故的概率與損失，各單元為了預防事故多米諾效應而進行的安全投入等因素。

2)應用博弈模型建立相鄰2單元的博弈支付矩陣。討論2單元選擇不同策略時，各單元的支付值函數表明，各單元選擇的安全投入策略不同，為此付出的代價(支付值)不同。

3)討論不同的參數條件下博弈模型的納什均衡點。將博弈模型分為4種情形并確定每種情形下的納什均衡點，將每種情形對應的納什均衡點與園區管理者希望的均衡點進行比較，為園區管理者是否采取激勵措施提供依據。

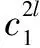
[1]段雅楠. 保障園區安全 共享發展紅利——訪中國石油和化學工業聯合會化工園區工作委員會秘書長楊挺[J]. 現代職業安全, 2016(9):14-17.

DUAN Ya’nan. Safety of the park Sharing development dividends[J].Modern Safey, 2016(9):14-17.

[2]國家安全生產監督管理總局.天津港“8·12” 瑞海公司危險品倉庫特別重大火災爆炸事故調查報告[EB/OL].2016.http://www.chinasafety.gov.cn/newpage/newfiles/201600812baogao.pdf.

[3]Fu G, Wang J, Yan M. Anatomy of Tianjin Port fire and explosion: Process and causes[J]. Process Safety Progress, 2016, 35(3):216-220.

[4]孫康,周武,柴瑞瑞. 化工園區危險化學品事故多米諾效應的網絡演化模型[J]. 電子科技大學學報(社科版),2015,17(5):37-41.

SUN Kang，ZHOU Wu，CHAI Ruirui. Network evolution model of hazardous chemical accident with domino effect in chemical industry park[J].Journal of UESTC(Social Sciences Edition),2015,17(5):37-41.

[5]李樹謙, 胡兆吉. 化工園區多米諾事故風險分析方法研究[J]. 安全生產與監督, 2008(3):56-58.

LI Shuqian, HU Zhaoji. Study on the risk analysis method of domino accident in chemical park[J]. Work Safety & Supervision, 2008(3):56-58.

[6]羅杰·B·邁爾森.博弈論:矛盾沖突分析[M].北京:中國人民大學出版社,2015.

[7]謝識予.經濟博弈論[M].上海:復旦大學出版社,2002.

[8]Nadeau S. Cooperation in health and safety:a game theory analysis[J].Law Rev (Risks),2003，1(3/4): 219-227.

[9]Reniers G. An external domino effects investment approach to improve cross-plant safety within chemical clusters[J]. Journal of Hazardous Materials, 2010, 177(1-3):167.

[10]宗翔,張冬梅,黃宏偉.博弈論在隧道及地下工程風險應對中的應用[J].地下空間與工程學報，2012，8(S2):1764-1765.

ZONG Xiang, ZHANG Dongmei, HUANG Hongwei. Application of game theory to risk response strategies in tunnel and underground engineering[J]. Chinese Journal of Underground Space and Engineering，2012,8(S2):1764-1765.

[11]李路, 周渝慧. 博弈論在處理大電網事故中的應用[J]. 東北電力技術, 2005, 26(4):25-27.

LI Lu，ZHOU Yuhui. The application of game theory to the handling of power grid collapse[J].Northeast Electric Power Technology， 2005, 26(4):25-27.

[12]Reniers G L L, Ale B J M, Dullaert W, et al. Designing continuous safety improvement within chemical industrial areas[J]. Safety Science, 2009, 47(5):578-590.

[13]Reniers G, Pavlova Y. Using Game Theory toimprove safety within chemical industrial parks[M]. London: Springer, 2013.

[14]Reniers G, Cuypers S, Pavlova Y. A game-theory based Multi-plant Collaboration Model (MCM) for cross-plant prevention in a chemical cluster.[J]. Journal of Hazardous Materials, 2012, 209-210(1):164-176.