一類跳頻序列集的最優(yōu)構造

黃 波 張小華

(成都東軟學院 四川 成都 611844)

一類跳頻序列集的最優(yōu)構造

黃 波 張小華

(成都東軟學院 四川 成都 611844)

跳頻擴頻是主要的擴頻編碼技術之一，跳頻序列在跳頻碼分多址系統(tǒng)中的作用至關重要。分圓理論由于具有良好的特性，在組合設計、良好的二元隨機序列設計中得到了廣泛應用。基于分圓理論，構造了一類關于Peng-Fan界最優(yōu)的跳頻序列集，節(jié)省了一個頻隙，豐富了跳頻序列集的構造方法。結果表明，該構造方法簡單易行，對跳頻通信系統(tǒng)性能的提高具有一定的指導意義。

跳頻序列集 彭-范界 分圓理論 周期漢明相關 碼分多址

0 引 言

在無線通信系統(tǒng)中，跳頻擴頻和直接序列擴頻是兩種主要的擴頻技術。跳頻碼分多址由于具有安全性、抗多址干擾等特性，其在藍牙、軍事無線電通信、移動通信以及現(xiàn)代雷達、聲吶系統(tǒng)中得到了廣泛應用[1]。通常情況下，如果兩個或多個發(fā)送者在同一時隙發(fā)送相同的頻隙，那么就產(chǎn)生了一次碰撞，相互之間的干擾就產(chǎn)生了。跳頻序列用來指定在每個時隙被傳輸?shù)念l隙，所以，多個發(fā)送者之間的相互干擾與跳頻序列之間的漢明相關是密切相關的，因而選擇碰撞次數(shù)少的跳頻序列(跳頻序列集)有利于跳頻通信系統(tǒng)性能的提高。好的跳頻序列(跳頻序列集)應具有以下特征：盡可能小的漢明相關特性；好的平衡性；盡可能長的周期；盡可能多的序列數(shù)目；盡可能大的復雜度；實現(xiàn)簡單。

目前，一部分最優(yōu)的跳頻序列集已被學者們進行了廣泛而深入的研究，例如：2011年，Zhou等[2]利用d型函數(shù)及線性方程組的解等相關知識構造了三類關于Peng-Fan界[3]最優(yōu)的跳頻序列集，并討論了所構造序列集的線性復雜度；2010年，Ding等[4]提出了基于編碼理論構造跳頻序列集的方法，拓展了跳頻序列集設計的方法，其他構造方法請參考相關文獻。分圓類在組合設計，二元序列設計中得到了廣泛的運用，學者們對利用分圓理論來構造最優(yōu)跳頻序列集進行了相應研究。對于有限域Fq，q是素數(shù)或素數(shù)方冪，令q-1=ef,2005年，Chu等[5]首次利用分圓理論構造出了兩類關于Lempel-Greenberger 界[6]最優(yōu)的跳頻序列，其序列長度為q，頻隙個數(shù)為e+1；之后，基于分圓理論的跳頻序列集基本上是在Chu方法上的引申；2008年，基于分圓理論和離散對數(shù)函數(shù),Ding等[7]提出了一種最優(yōu)的跳頻序列設計方法，構造的序列長度為q-1，頻隙個數(shù)為e+1；2009年，Zhang等[8]利用分圓理論、離散對數(shù)函數(shù)以及中國剩余定理,構造出了一類最優(yōu)的跳頻序列以及跳頻序列集，序列長度為2(q-1)頻隙個數(shù)為e+1；對于素數(shù)p，2013年WenliRen[9]推廣了Zhang和Ding的方法，構造出了一類最優(yōu)的跳頻序列集，序列的長度為p(q-1)，頻隙個數(shù)為e+1。2013年Liu等[10]提出了一種關于平均周期漢明相關界最優(yōu)的跳頻序列集, 同時研究了所構造的跳頻序列集的漢明相關分布。本文中，我們利用分圓理論，提出了一種關于Peng-Fan界[3]最優(yōu)的跳頻序列集，序列的長度為q，頻隙個數(shù)為e，顯然，我們的方法節(jié)省了一個頻隙，構造簡單易行，具有一定的參考價值。

1 基本概念

在本文中，我們用符號(N,M,q,λ)表示長度為N，具有M個跳頻序列，頻隙集中頻隙個數(shù)為q，最大周期漢明相關為λ的跳頻序列集。用符號(l,q,h)表示長度為l，頻隙集中頻隙個數(shù)為q，最大周期漢明自相關為h的跳頻序列。

令F={f1,f2,…,fq}是一個具有q個頻隙的頻隙集,S是一個具有M個長度為N的跳頻序列集,對于任意兩個頻隙f1、f2,令：

(1)

對于任意兩個跳頻序列x=(x0,x1,…,xN-1),y=(y0,y1,…,yN-1), 任意正整數(shù)τ，N0≤τ≤N，序列x和y在時延τ時的周期漢明相關定義如下：

(2)

這里，所有的下標運算都是在模N下進行的。

對于任意給定的跳頻序列集S，最大周期漢明自相關Ha(S)和最大周期漢明互相關Hc(S)分別定義如下：

(3)

最大周期漢明相關Hm(S)定義如下：

Hm(S)=max{Ha(S),Hc(S)}

(4)

1974年，LempelandGreenberger[6]建立了關于單個跳頻序列漢明自相關的理論界。

引理1(Lempel-Greenberger界[6])：對于長度為N，定義在具有q個頻隙的頻隙集上的任意跳頻序列，漢明自相關滿足下面的界：

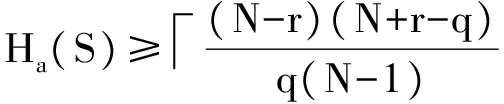
(5)

這里，r是N模q的最小非負剩余。顯然，Lempel-Greenberger界沒有涉及跳頻序列的個數(shù)。

定義1 對于任意跳頻序列(l,q,h)，若h-1使Lempel-Greenberger界(5)中的等號成立，則該序列關于Lempel-Greenberger界是漸進最優(yōu)的。

2004年，PengandFan[3]引入跳頻序列個數(shù)M，建立了在跳頻序列集設計中廣泛使用的關于最大周期漢明相關的理論界。

引理2(PengandFan界[3])：令S是一個長度為N，具有M個跳頻序列，定義在具有q個頻隙的頻隙集上的跳頻序列集，我們有：

(6)

和：

(7)

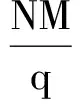
定義2 對于任意跳頻序列集(N,M,q,λ)，若λ使PengandFan界(式(6)、式(7))中的等號成立，則該跳頻序列集關于PengandFan界是最優(yōu)的。

2 最優(yōu)跳頻序列集構造

該部分，我們利用分圓理論[11]構造了一類關于Peng-Fan界最優(yōu)的跳頻序列集。

令Fq是一個具有q個元素的有限域，同時設存在兩個正整數(shù)e和f，滿足ef=q-1,α是有限域Fq的一個本原元。C0=〈αe〉是由αe產(chǎn)生的Fq的乘法子群，有限域Fq的e階分圓類定義如下：

Ci={αi+ks:i=0,…,e-1;k=0,…,f-1}

(8)

對于0≤i≠j≤e-1,有：

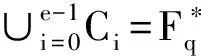
(9)

對于任意正整數(shù)n，Ci+ne=Ci。進一步，關于有限域Fq的e階分圓數(shù)定義如下：

(10)

顯然，最多有e2個不同的e階分圓數(shù)。

我們將會利用下面的引理來計算所設計的跳頻序列集的漢明自相關和漢明互相關。

引理3 令q=ef+1是一個素數(shù)或素數(shù)方冪，Ci是有限域Fq的e階分圓類，我們有：

(11)

本文構造最優(yōu)跳頻序列集的方法如下：

Step1 選擇一個素數(shù)或素數(shù)方冪q，選擇兩個正整數(shù)e和f，滿足q-1=ef，設Ci是有限域 Fq的e階分圓類。

Step2 對于0≤i≤e-1，利用分圓類Ci得到如下的數(shù)集

顯然下式成立：

(12)

(13)

其中：0≤k≤e-1。

定理1 根據(jù)Peng-Fan界，我們有：如果λ∈Ze,當f是偶數(shù)時,S是一個最優(yōu)的跳頻序列集，其參數(shù)為(q,e,e,f+1)。根據(jù)Lempel-Greenberger界：跳頻序列集S中的每個跳頻序列是漸進最優(yōu)的。

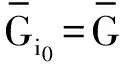
=f-1+Δ

(14)

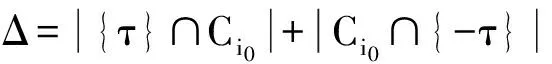
下面我們確定Δ的值。

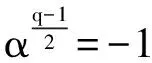
1) 如果τ和-τ均屬于分圓類Ci0。

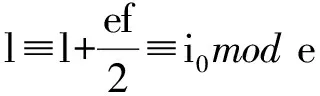
Hsi(τ)=f+1

(15)

2) τ和-τ之一屬于Ci0，或者τ和-τ均不屬于Ci0。

因為τ取遍{1,2,…,q-1}中的每個值，顯然存在這樣的τ，使這兩種情況都成立，所以：

(16)

對于0≤u≤e-1，令si、si+u是跳頻序列集S中的任意兩個跳頻序列，根據(jù)周期漢明互相關的定義，在時延τ時，我們有：

(17)

為了計算Hsi,si+u(τ)的值，我們分以下三種情況討論。

1) 當τ跑遍{1,2,…,q-1}時，若存在τ，使τ∈Ci0+u，且-τ∈Ci0-u成立，則必有：

(18)

所以：

(19)

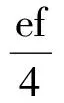
Hsi,si+u(τ)=f

(20)

2) 當τ跑遍{1,2,…,q-1}時，存在l≡i0+umode，使得τ∈Ci0+u。

Hsi,si+u(τ)=f+1

(21)

Hsi,si+u(τ)=f+1

(22)

基于以上分析，跳頻序列集S的最大周期漢明相關為：

Hm(S)=f+1 0≤τ≤q-1

(23)

下面分析跳頻序列集S關于Peng-Fan界是最優(yōu)的。把相關參數(shù)代入Peng-Fan界有：

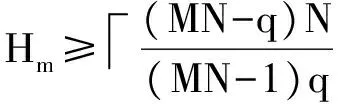
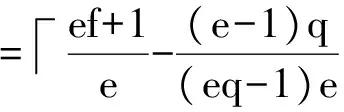
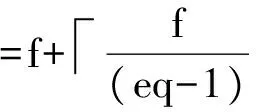
(24)

顯然，達到了Peng-Fan界的下界，所以關于Peng-Fan界，S是最優(yōu)的跳頻序列集。

由于對于任意的q，均有q≡1mode，故r=1。把相關參數(shù)代入Lempel-Greenberger界有：

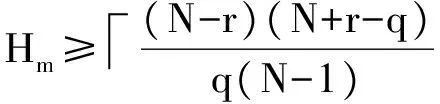
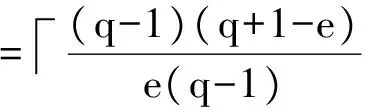
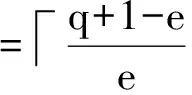
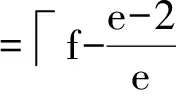
(25)

其中，Hm(S)-1使Lempel-Greenberger界中的等號成立，故S中的每個跳頻序列是漸進最優(yōu)的。

定理得證。

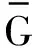
令S(19)=2，得到長度為19，個數(shù)為3，定義在有限域F19上的跳頻序列集為:

對于時延τ，0≤τ≤18，漢明相關分別如下：

漢明自相關為：

Hs1(τ)={5,5,5,7,5,7,5,5,7,7,5,5,7,5,7,5,5,5}

Hs2(τ)={7,5,5,5,5,5,7,7,5,5,7,7,5,5,5,5,5,7}

Hs3(τ)={5,7,7,5,7,5,5,5,5,5,5,5,5,7,5,7,7,5}

漢明互相關為：

Hs1,s2(τ)={7,6,6,7,6,7,7,7,7,7,7,7,7,6,7,6,6,7,1}

Hs1,s3(τ)={6,7,7,7,7,7,6,6,7,7,6,6,7,7,7,7,7,6,1}

Hs2,s1(τ)={7,6,6,7,6,7,7,7,7,7,7,7,7,6,7,6,6,7,1}

Hs2,s3(τ)={7,7,7,6,7,6,7,7,6,6,7,7,6,7,6,7,7,7,1}

Hs3,s1(τ)={7,7,7,6,7,6,7,7,6,6,7,7,6,7,6,7,7,7,1}

Hs3,s2(τ)={6,7,7,7,7,7,6,6,7,7,6,6,7,7,7,7,7,6,1}

最大周期漢明相關為：

Hm(S)=7

可以驗證，關于Peng-Fan界，S是最優(yōu)的跳頻序列集。關于Lempel-Greenberger界，S中每個跳頻序列是漸進最優(yōu)的。

3 結 語

基于分圓理論，提出了一種關于Peng-Fan界最優(yōu)的跳頻序列集的構造方法。本文所構造的跳頻序列集與參考文獻中所構造的跳頻序列集的相關比較如表1所示。

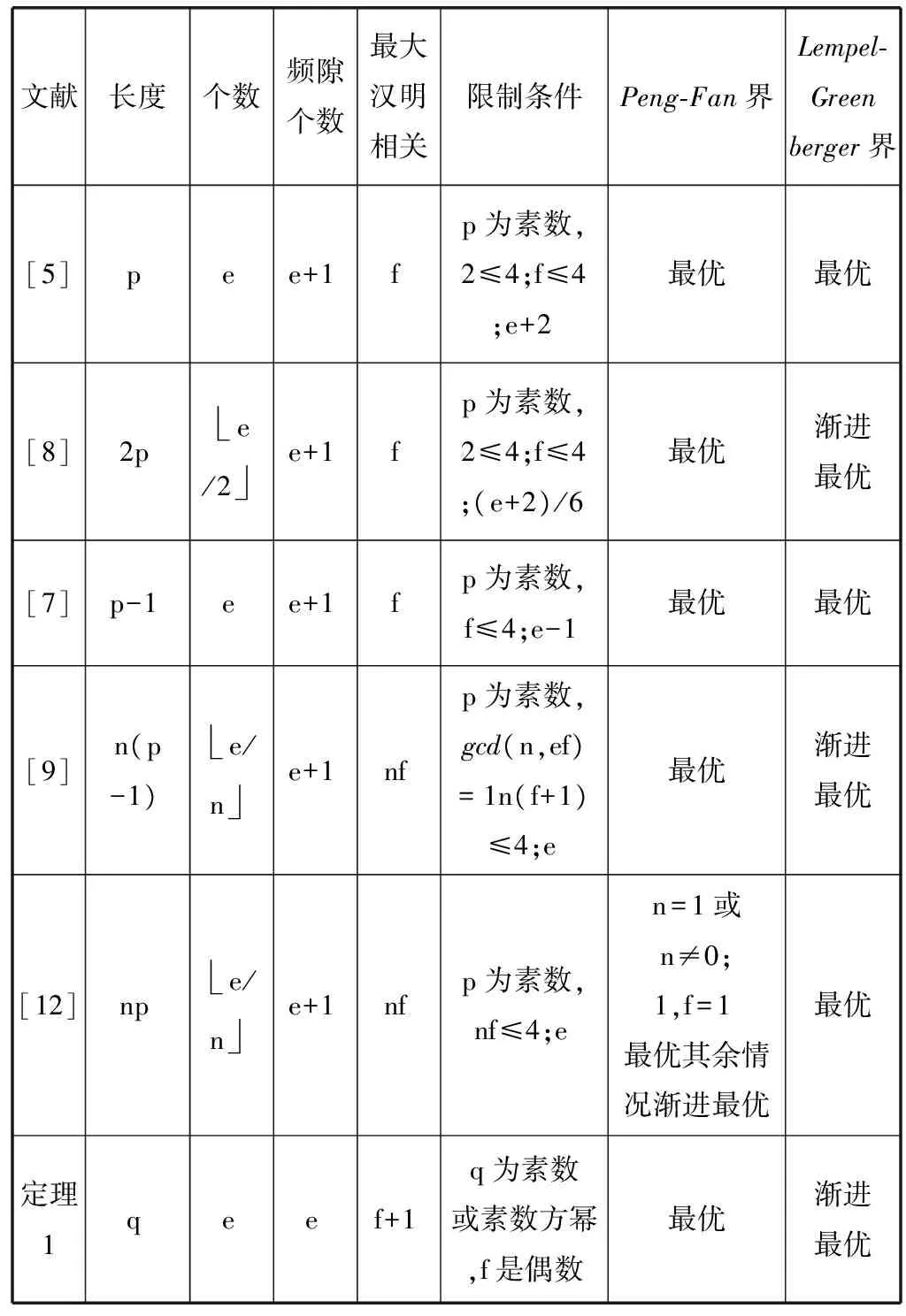
表1 本文構造的跳頻序列集與已知跳頻序列集的比較

本文方法簡單易行，豐富了跳頻序列集的構造方法。利用分圓理論構造更多最優(yōu)的其它類跳頻序列集將是我們進一步研究的內容。

[1] Fan P Z,Darnell M.Sequence Design for Communications Applications[M].Research Studies Press (RSP),Wiley,London (1996).

[2] Zhengchun Zhou,Xiaohu Tang,Daiyuan Peng,et al.New constructions for optimal sets of frequency hopping sequences[J].IEEE Transactions On Inform.Theory,2011,57(6):3831-3840.

[3] Daiyuan Peng,Pingzhi Fan.Lower bounds on the Hamming auto-and cross correlations of frequency-hopping sequences[J].IEEE Transactions on Information Theory,2004,50(9):2149-2154.

[4] Cunsheng Ding,FujiHara,R Fujiwara,et al.Sets of frequency hopping sequences:bounds and optimal constructions[J].IEEE Trans Inform Theory,2009,55(7):3297-3304.

[5] Chu W,Colbourn C J.Optimal frequency-hopping sequences via Cyclotomy[J].IEEE Transactions on Information Theory,2005,51(3):1139-1141.

[6] Lempel A,Greenberger H.Families of sequences with optimal Hamming correlation properties[J].IEEE Transactions on Information Theory,1974,20(1):90-94.

[7] Cunsheng Ding,Jianxing Yin.Sets of optimal frequency-hopping sequences[J].IEEE Transactions on Information Theory,2008,54(8):3741-3745.

[8] Yun Zhang,Pinhui Ke,Shengyuan Zhang.Optimal frequency hopping sequences based on Cyclotomy[C]//First International Workshop on Education Technology and Computer Science,2009,1:1122-1126.

[9] Wenli Ren,Fangwei Fu,Zhengchun Zhou.New sets of frequency-hopping sequences with optimal Hamming correlation[J].Des.Codes Cryptogr,2014,72(2):423-434.

[10] Fang Liu,Daiyuan Peng,Zhengchun Zhou.A new frequency-hopping sequence set based upon generalized Cyclotomy[J].Des. Codes Cryptogr,2012,69(2):247-259.

[11] Storer T.Cyclotomy and Difference Sets[M].Chicago,IL:Markham,1967.

[12] 徐善頂,曹喜望,許廣魁.一類周期為素數(shù)倍數(shù)的跳頻序列集[J].電子學報,2015,43(10):1930-1935.

OPTIMAL CONSTRUCTION OF FREQUENCY-HOPPING SEQUENCE SETS

Huang Bo Zhang Xiaohua

(ChengduNeusoftUniversity,Chengdu611844,Sichuan,China)

Frequency-hopping (FH) spread spectrum is one of the main spread spectrum coding technologies. Furthermore, frequency-hopping sequences (FHS) play important roles in FH code division multiple access systems. Due to its good characteristics, the cyclotomy has been widely used in combinatorial designs and good designs of binary random sequences. Based on cyclotomy, a class of FHS set with Peng-Fan bounds is constructed, which can save a frequency gap and enrich the construction methods of FHS sets. The results show that this method is simple and easy to be implemented, and it has a certain guiding significance for improving the performance of FH communication system.

Frequency hopping sequence set Peng-Fan bound Cyclotomy Periodic hamming correlation Code division multiple access

2016-03-08。黃波，講師，主研領域：網(wǎng)絡通信，數(shù)字圖像處理，軟件工程。張小華，講師。

TP393.04

A

10.3969/j.issn.1000-386x.2017.03.022