云環境下基于多目標優化的科學工作流數據布局策略

程慧敏 李學俊,* 吳 洋 朱二周

1(安徽大學計算機科學與技術學院 安徽 合肥 230601)2(安徽大學計算智能與信號處理重點實驗室 安徽 合肥 230039)

云環境下基于多目標優化的科學工作流數據布局策略

程慧敏1李學俊1,2*吳 洋1朱二周2

1(安徽大學計算機科學與技術學院 安徽 合肥 230601)2(安徽大學計算智能與信號處理重點實驗室 安徽 合肥 230039)

針對傳統科學工作流數據布局策略在減少數據傳輸時間的同時，不能兼顧數據中心間的負載均衡，提出一種基于多目標優化的數據布局策略。首先生成固定數據集布局方案，然后利用多目標優化算法KnEA對非固定數據集進行布局，最終得到全局布局方案。KnEA算法利用knee points比普通非支配個體有著更好的收斂性特征，并綜合考慮多個優化目標間的平衡，因而可以取得數據傳輸時間和負載均衡都很好的數據布局方案。通過對比實驗證明了該數據布局策略的有效性。

云計算 科學工作流 數據布局 多目標優化 負載均衡

0 引 言

在現代科學應用領域中天文學[1]、高能物理學[2]、生物信息學[3]等通常都是計算密集型和數據密集型的應用，它們往往包含成千上萬個任務，并且需要處理TB級或者PB量級的數據，因而需要大量的計算資源和存儲資源。科學工作流作為一種重要的機制可以幫助科學家自動執行這些科學仿真和數據分析過程[4]。目前，許多科學家通常將科學工作流部署在網格和集群等分布式環境上。然而，建立這樣的系統是非常昂貴的，而且申請訪問這些系統也需要花費大量的時間[8]。云計算技術在2007年被提出[5]，由于它擁有全球性的分布式數據中心，因而能夠支持大規模的應用的快速發展[6]。云計算能夠為用戶提供大量的存儲空間和高性能的計算資源，并以按量付費的方式收取費用。它的高效、靈活的特點為科學工作流的執行提供了一種全新的方式[7]。

云計算環境下的數據中心都有它獨特的特征，例如存儲空間和計算能力。由于這些特征的限制，將科學工作流中大量的數據集存放在某個數據中心是不合理的[10]。因此，將科學工作流部署在云計算平臺上面臨著數據布局方面的挑戰。數據布局問題是在滿足數據中心容量要求的前提下，將數據集布局到數據中心上。顯然，它是NP難問題，因此可以簡化成背包問題。目前存在的數據布局策略主要是基于聚類算法[8,11]和智能算法[10]，包括k-means算法，數據集和任務協同調度算法，遺傳算法GA(Genetic Algorithm)和PSO(Particle Swarm Optimization)算法等，其中k-means算法[8]是最具代表性的算法。k-means算法和GA算法可以將依賴關系強的數據集布置在同一個數據中心上，從而減少科學工作流執行過程中數據傳輸時間。但它們忽略了數據中心間負載均衡，導致數據集被布局在少量的數據中心上，從而影響了整個數據中心的計算能力，進而降低了科學工作流的執行效率。因此，一個高效的數據布局策略應同時兼顧到數據傳輸時間和數據中心間的負載均衡。

基于上述的分析，對數據集進行布局時，同時考慮數據傳輸時間和負載均衡是很困難的，傳統的數據布局方法很難獲取高效的數據布局方案。本文運用基于進化算法的多目標優化方法[9]對數據集進行布局。多目標優化方法即同時優化多個目標的算法，它綜合考慮多個優化目標間的權衡，并能夠最終獲得一組最優解。故利用多目標優化方法可以兼顧數據布局策略中的數據傳輸時間和負載均衡。解決多目標優化問題通常采用的是基于進化算法的啟發式方法，它有著自適應、避免局部最優、黑盒式求解等諸多優點[14]，可以有效解決科學工作流中數據布局問題。

1 相關工作

科學工作流的數據布局是一個非常重要且富有挑戰性的問題，它對于減少科學工作流的執行費用和提高科學工作流的執行效率有著重要的意義，因此，合理的數據布局策略至關重要。目前已有學者對此進行了探索和研究，主要包括聚類算法[8,11]和智能算法[10]的數據布局策略的相關研究。此外，我們將介紹基于進化算法的多目標優化方法。

在聚類算法方面，文獻[8]提出了一種基于k-means算法的數據布局策略。該策略首先建立數據依賴矩陣，矩陣中每個元素表示兩個數據集的公共任務個數。然后利用BEA算法對依賴矩陣進行聚類變換得到聚類矩陣，然后將聚類矩陣劃分成若干個集合。最后將劃分的集合布局至相應的數據中心，這樣就盡可能將依賴度高的數據集布局在同一個數據中心，從而減少了數據傳輸時間。文獻[11]提出了一種基于圖切割的任務和數據集協同調度策略。它根據數據集的固定存儲特征將數據起源圖切割成子圖，并不斷重復這個過程直到該子圖所包含的數據集能夠滿足數據中心的容量要求，最后將任務和數據集布局到合理的數據中心。在智能算法方面，文獻[10]在能夠反映負載均衡和數據傳輸時間兩目標的適應值函數的基礎上，使用遺傳算法對科學工作流中數據集進行布局，該方法在負載均衡方面和負載均衡方面均取得了很好的效果。

上述的數據布局策略要么從單一目標(例如數據傳輸時間)來考慮科學工作流的數據布局問題，要么雖然考慮了數據傳輸時間和負載均衡兩個目標，但不能夠對數據傳輸時間和負載均衡兩個目標同時進行優化，因而都不能夠有效地提高科學工作流的執行效率。基于進化算法的多目標優化方法可同時優化多個目標，因而，可以有效解決數據布局中數據傳輸時間和負載均衡不能同時兼顧的難題。多目標優化問題在工程學，生物學和經濟學等領域中非常普遍[12-15]。多目標優化問題中各個目標間通常是互相矛盾的，目標函數可能具有多峰、不連續、不可導甚至離散等特點，無法通過傳統的最優化方法或算法來解決。作為一種啟發式的智能搜索算法，進化算法能有效地解決多目標優化問題并已經得到了越來越多的研究證明[17]。

在多目標優化方法方面，文獻[15]提出了一種基于非支配排序的多目標優化算法(NSGA-II)，它利用非支配排序算法以及擁擠距離策略，從當前父子代的聯合種群中選出參與下一代進化的種群，兼顧了種群的收斂性與分布性。文獻[9]在NSGA-II 研究和分析的基礎上，提出的一種基于knee points的多目標優化算法(KnEA)。knee points是前沿面上具有更好收斂性的一些個體。該算法通過一種自適應的方法識別出種群中的knee points，并在交配池選擇和環境選擇操作中優先考慮它們，從而加速種群的收斂和維護種群的多樣性。與多個主流的多目標進化算法的實驗對比說明，KnEA能在多目標優化問題上獲得更好的性能表現。

本文在對數據集進行布局時，將綜合考慮數據傳輸時間和負載均衡兩個重要因素。運用基于進化算法的多目標優化方法(KnEA)對數據集進行布局，從數據傳輸時間和負載均衡兩個方面對數據布局方案進行同時優化，取得了顯著的效果。

2 科學工作流的描述和問題分析

首先介紹云計算環境下科學工作流數據布局問題的相關定義，具體包括云環境、科學工作流、數據集、任務。然后對數據布局中所面臨的問題進行分析。

2.1 相關定義

定義1 云計算環境表示為多個分布式數據中心組成的集合DC={dc1,dc2,…,dcm}。單個數據中心dci可表示為dci={size,cap},其中size表示數據中心dci的容量,cap表示數據中心dci的計算能力，并用執行同一任務所需的時間的倒數來量化表示。

定義2 科學工作流定義為G={T,C,DS}。其中T={t1,t2,…,tn}表示工作流G的所有任務，C表示任務之間控制流的鄰接矩陣，DS={d1,d2,…,dn}表示G中所有數據集的集合。

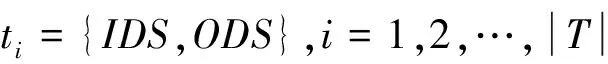
定義4 根據數據集存放位置是否受限，可以將數據集分為固定數據集和非固定數據集。將DS中所有固定數據集組成的集合記為DSfix。對?di∈DSfix，記di指定存放的數據中心編號為fix_loc(di)。DS中所有非固定數據集組成的集合記為DSflex。

2.2 問題分析

下面給出一個簡單的科學工作流的實例如圖1所示，假設云計算平臺有兩個數據中心dc1、dc2，該科學工作流有6個數據集d1、d2、d3、d4、d5、d6，每個數據集大小均為1GB,其中d2是存放在數據中心dc1上的固定數據集，d6是存放在數據中心dc2上的固定數據集。

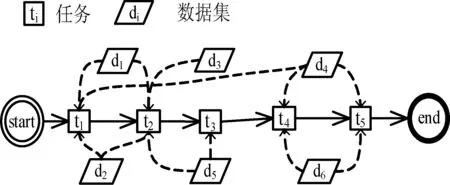
圖1 科學工作流實例

對于圖1中科學工作流，基于k-means算法的數據布局策略得到數據布局方案，如圖2(a)所示。接著從優化數據傳輸時間和負載均衡的多目標優化角度出發，得到優化后的數據布局方案如圖2(b)所示。

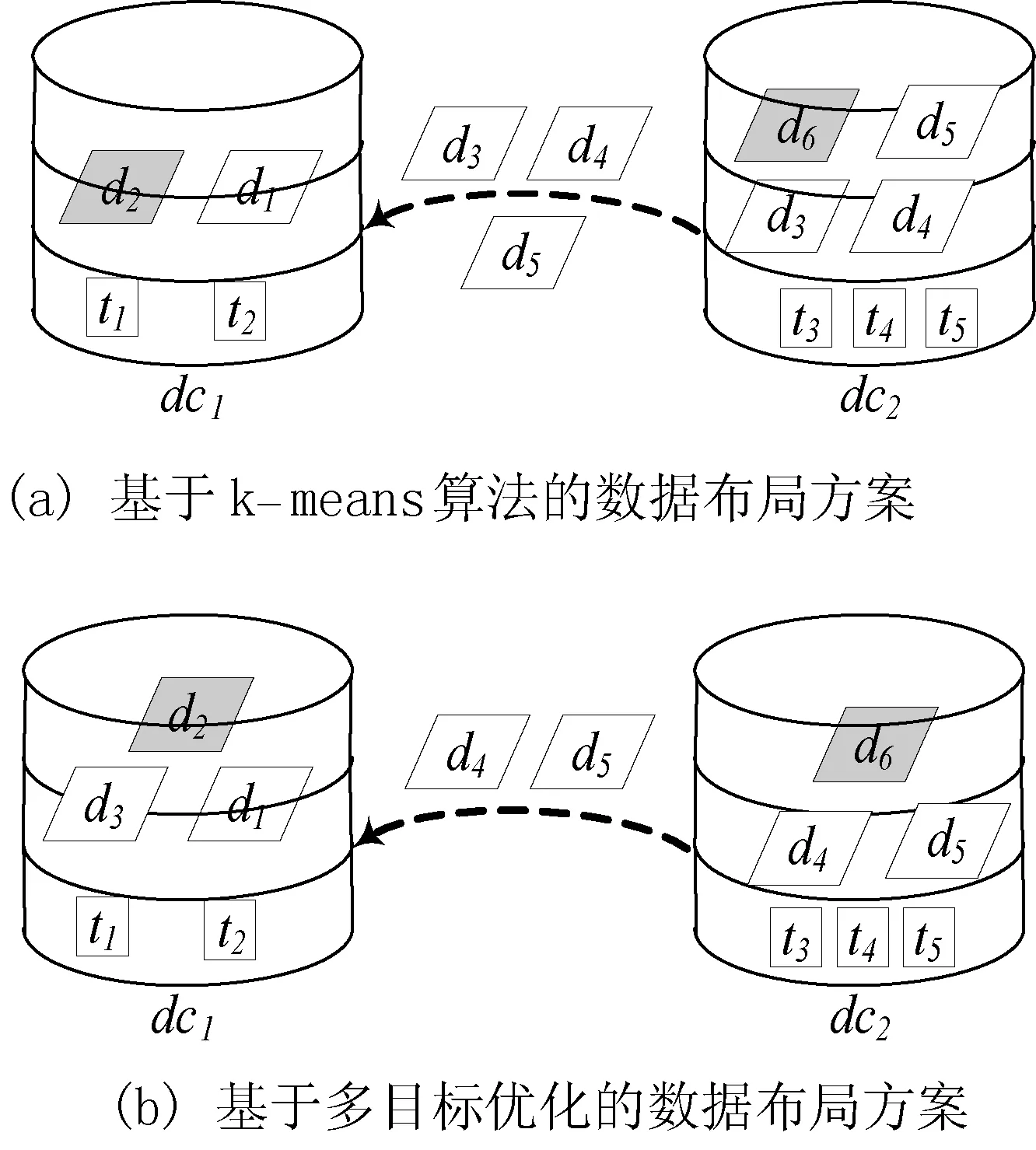
圖2 兩種數據布局方案

根據將數據集進行跨數據中心的傳輸代價比任務調度的代價大這一原則[8]，在上述兩種數據布局方案中，將任務t1、t2調度到數據中心dc1，任務t3、t4、t5調度到數據中心dc2。基于k-means算法的數據布局方案在科學工作流的執行過程中，數據集d3、d4、d5,從數據中心dc2傳輸到數據中心dc1，需要的傳輸量為3GB；數據中心dc1的負載量為2GB,dc2的負載量為4GB,因此數據中心間負載不能保持均衡。基于多目標優化的數據布局方案在科學工作流執行過程中，數據集d3、d4從數據中心dc2傳輸到數據中心dc1，需要的傳輸量為2GB，同比減少33%；數據中心dc1和dc2的負載量均為3GB，因此數據中心間負載保持均衡。因而，基于k-means算法的數據布局策略不能很好地解決數據布局問題。

3 基于多目標優化的數據布局算法

運用基于多目標優化的數據布局算法對科學工作流中數據集進行布局，它在減少數據傳輸時間的同時，兼顧了數據中心間負載均衡。下面將首先介紹數據布局方案的數據傳輸時間和負載均衡兩種評價指標，然后給出數據布局算法。

3.1 數據布局評價指標

數據傳輸時間：采用將任務調度至執行該任務所需數據傳輸時間最小的數據中心的任務調度策略。如果每個任務需要的數據集不在該任務存放的數據中心，則需要從其它數據中心進行傳輸。數據傳輸時間即科學工作流全部執行時，所有任務需要的跨數據中心間數據集傳輸時間之和。

Time(dk,dci,dcj)表示dk從源數據中心dci傳輸到目標數據中心dcj所需要的時間,如式(1)所示。

Time(dk,dci,dcj)=dk·ds/bij

(1)

其中，bij表示數據中心dci和數據中心dcj間的帶寬。Time(ti,dci)表示當任務ti調度到數據中心dci時，ti所需的輸入數據集不在dci時，要從其他數據中心傳輸數據集所需的時間之和。如式(2)所示。

(2)

工作流執行過程中，數據中心計算能力動態變化，負載均衡是一個動態的均衡。然而本文研究靜態數據布局方案，假設每個數據中心的計算能力相同，負載均衡僅和數據中心的存儲情況有關。文獻[10,11]采用數據中心使用率的標準差來描述數據中心間負載均衡，但數據中心的容量非常大，數據集大小對于數據中心的容量的比例很小，故計算結果并不準確，本文使用數據中心使用量的標準差來描述數據中心間負載均衡，如式(3)所示。

(3)

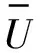
(4)

3.2 數據布局算法

下面首先對數據布局方案的編碼規則進行介紹，然后給出本文的數據布局算法。

3.2.1 編碼規則

常見的編碼規則有二進制編碼、格雷碼編碼、符號編碼、浮點數編碼和整數編碼等[16]。本文采用整數編碼規則，每個個體代表一個數據布局方案。通過整數編碼規則，可以避免出現將數據集布局到編號不存在的數據中心上的無效個體。假設有m個數據中心和n個數據集，代表數據布局方案的個體由n個整數組成:(g1,g2,…,gn)1≤gj≤m(j=1,2,…,n)gj表示第j個數據集所在的數據中心編號。

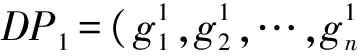
3.2.2 算法描述

本文的數據布局策略是首先將固定數據集布局到相應的數據中心得到固定數據集布局方案DPfix，然后運用多目標進化算法(KnEA)對非固定數據集進行布局得到非固定數據集布局方案DPflex，最后，對兩者進行合并，得到全局數據布局方案DP。

算法 基于KnEA的數據布局算法

輸入：數據中心集合DC，數據集合DS

輸出：數據布局方案DP

主要步驟：

1.DPfix=[DPfix,fix_loc(di)]?di∈DSfix;

2.P=random(DSflex,N);

//隨機生成N個個體

3.whilenottermination()do

4.Q=mating_selection(P,K,N);

//交配池選擇

5.Q=P∪variation(Q);

//子代交叉和變異處理

6.F=nondominated_sort(P);

//非支配排序

7. [K,r,t]=find_knee_point(F,T,r,t);

//查找kneepoints

8.P=environment_selection(F,K,N);

//自然選擇

9.end

10.DPflex=getbest(P)

//選出最佳的個體

11.DP=DPfix+DPflex;

12.ReturnDP;

第1行將固定數據集布局到該數據集指定存放的數據中心，得到固定數據集布局方案DPfix。

第2～12行得到非固定數據集布局方案DPflex，具體的，第2行隨機生成N個非固定數據集布局方案并記為P。第4～5行根據交配池選擇原則的三個準則即個體間的支配關系、個體是否為kneepoint以及個體的加權距離，則從P中選出N個個體記為Q,并對Q中個體進行交叉變異，然后和P中個體進行合并。第6行將P中個體進行非支配排序，并將排序后結果記為F。第7行將F中每個前沿面里符合kneepoint條件的個體放入到K中，其中r和t是自適應參數，T是算法中預設參數。第8行綜合F和K的結果，選出N個優秀的個體作為下一次迭代的輸入。算法的細節步驟參見文獻[9]。第10行表示從P中選出一個最佳的個體(即非固定數據集布局方案)DPflex。

第11行,將固定數據集布局方案DPfix和非固定數據布局方案DPflex進行合并，得到所有數據集的布局方案DP。

4 實 驗

將本文提出的基于多目標優化的數據布局策略(KnEA)和基于聚類算法的數據布局策略(k-means)[8]、基于遺傳算法的數據布局策略(GA)[10]進行對比試驗。隨機生成仿真科學工作流，然后使用本文策略、聚類策略和基于遺傳算法的數據布局策略得到各自的數據布局方案，運行仿真的科學工作流，并記錄該過程中數據傳輸時間和負載均衡。采用控制變量法給出數據集個數，數據中心個數，固定數據集比例變化時的數據傳輸時間和負載均衡如圖3-圖5所示。實驗過程中,隨機生成10個任務，數據集大小為10～1 000MB的科學工作流，數據中心間帶寬為10MB/s。KnEA算法迭代次數為100次，種群初始個體為20個，自適應參數r初始值設為1，t的初始值設為0，預設參數T設為0.5。遺傳算法的迭代次數為100次，種群初始個體為20個，變異概率為0.1。為了保證結果的可靠性，每一個科學工作流在保持實驗環境配置不變的情況下運行100次后取平均值作為測試結果。

4.1 數據集個數

圖3給出數據中心個數5個，固定數據集比例20%的情況下，隨著數據集個數的增加，數據傳輸時間和負載均衡的變化趨勢。在數據傳輸時間方面，本文的策略稍優于k-means策略；和GA策略比較，本文策略效果略差。但在負載均衡方面，當數據集個數大于30且不斷增加時，本文的策略優于k-means策略和GA策略，且優勢尤為明顯。

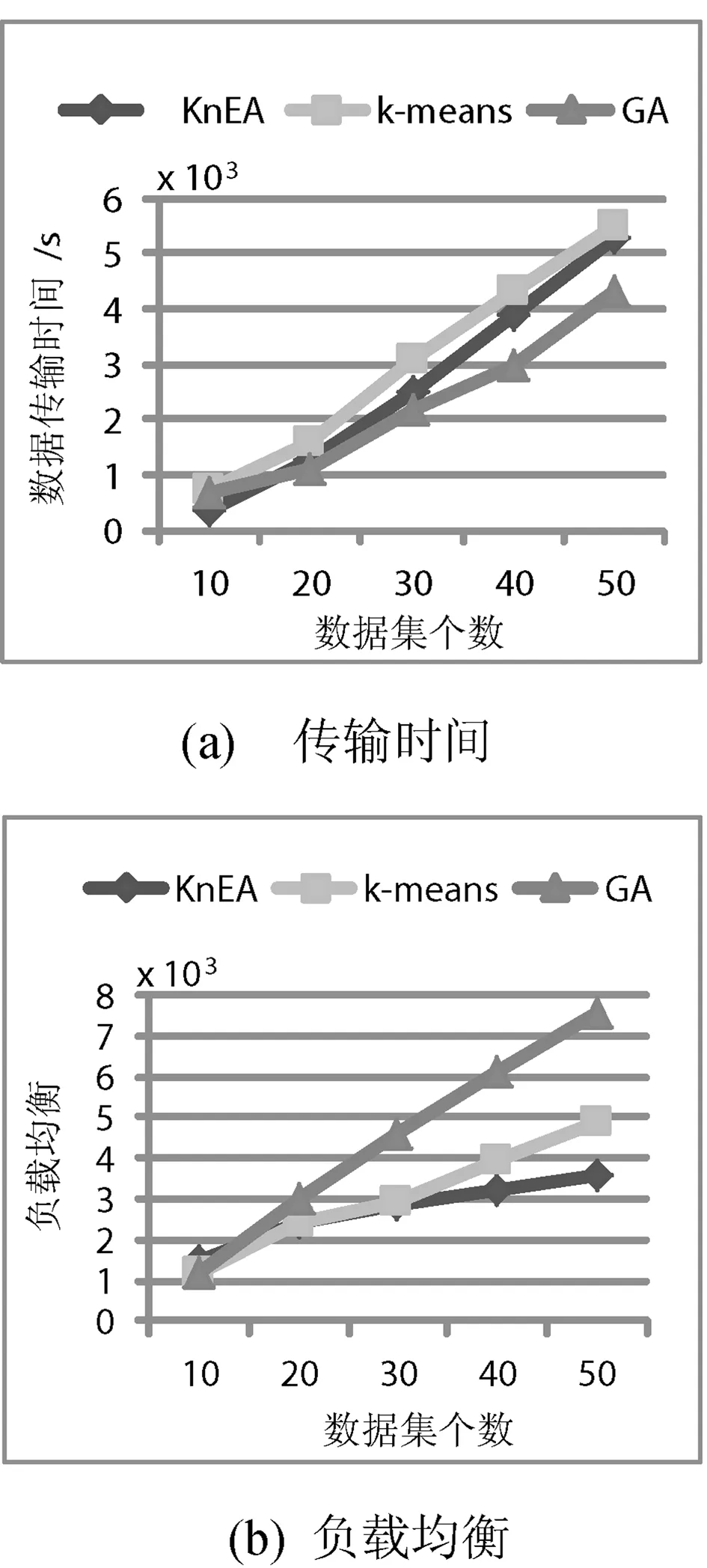
圖3 數據集個數

4.2 數據中心個數

圖4給出數據集個數40個，固定數據集比例20%的情況下，隨著數據中心個數的增加，數據傳輸時間和負載均衡的變化趨勢。本文的策略在數據傳輸時間方面介于k-means策略和GA策略之間。但在負載均衡方面，本文的策略要好于k-means策略，且相比GA策略，本文的策略優勢十分明顯。

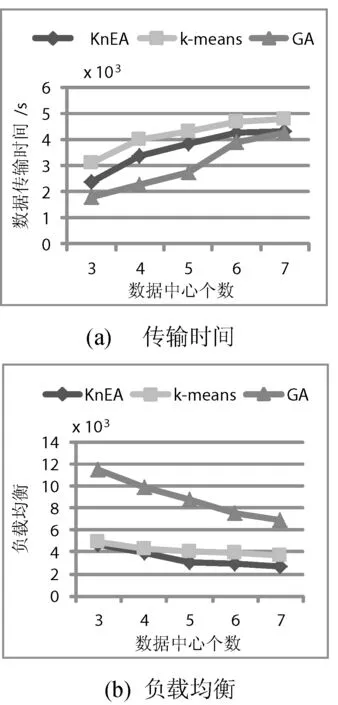
圖4 數據中心個數

4.3 固定數據集比例

圖5給出數據集個數40個，數據中心個數5個的情況下，隨著固定數據集比例的增加，數據傳輸時間和負載均衡的變化趨勢。在數據傳輸時間方面，本文的策略稍優于k-means策略，和GA策略基本持平。但在負載均衡方面，本文的策略要明顯好于GA策略，但并不優于k-means策略，這主要是由于隨著固定數據集比例的增大，更多的數據集存放在指定的數據中心，聚類的中心在增多，導致基于聚類的k-means數據布局策略更具優勢。

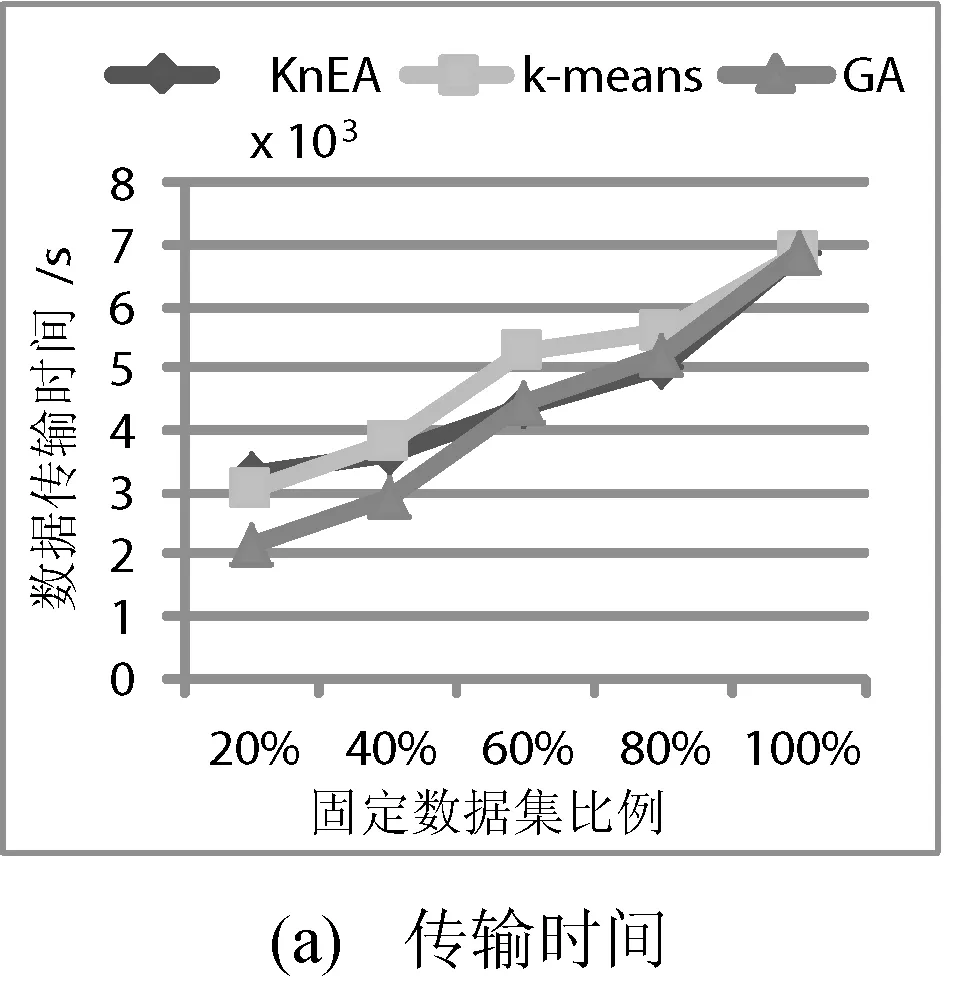
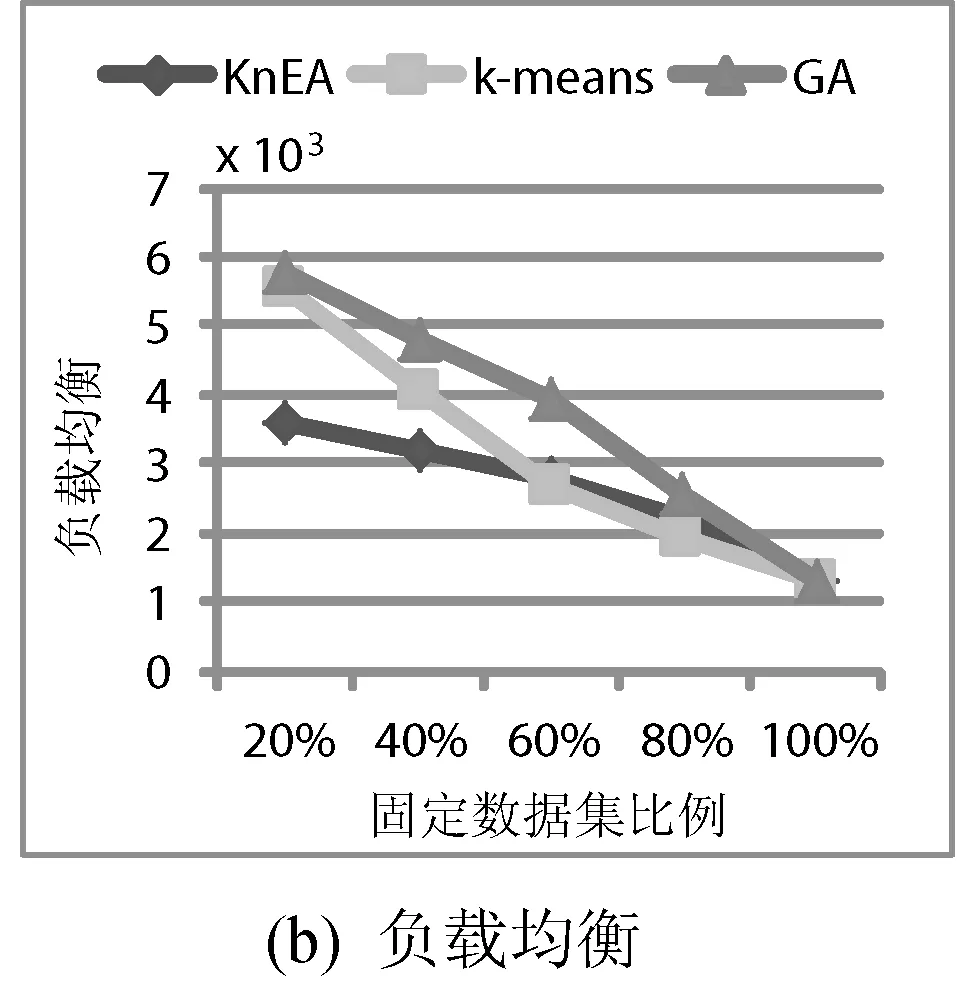
圖5 固定數據集比例

綜上，k-means策略和GA策略是能將依賴性較強的數據集布局在一起，使得數據集集中在較少的數據中心上。實驗結果顯示，它可以減少數據傳輸時間，但它導致更多的數據中心處于未利用狀態，從而使數據中心間負載失去平衡。而本文的數據布局策略從多目標優化思想出發，在數據傳輸時間方面與k-means策略和GA策略基本持平，具有同等的優勢，但在負載均衡方面明顯優于k-means策略和GA策略。因此，本文的數據布局策略可以有效提高科學工作流的執行效率。

5 結 語

本文首先分析了科學工作流在云計算平臺上運行時所面臨的挑戰，特別是對數據集進行布局時，不能在減少數據傳輸時間的同時保持數據中心間負載均衡。然后對該問題進行分析，并運用基于多目標優化的數據布局策略對數據集進行布局，并與聚類數據布局策略進行對比實驗。實驗結果表明，本文的策略不僅可以減少數據傳輸時間，而且在保持數據中心間負載均衡方面具有很大的優勢。未來我們計劃運用多目標進化算法對數據布局的同時，對任務進行調度。在減少數據傳輸時間和保持數據中心負載均衡的情況下，減少任務的執行時間，從而高效地提高科學工作流的執行效率。

[1]DeelmanE,BlytheJ,GilY,etal.Pegasus:Mappingscientificworkflowsontothegrid[C]//inEuropeanAcrossGridsConference.Nicosia,Cypurs,2004:11-20.

[2]LudascherB,AltintasI,BerkleyC,etal.ScientificworkflowmanagementandtheKeplersystem[J].ConcurrencyandComputation:PracticeandExperience,2005,18(10):1039-1065.

[3]OinnT,AddisM,FerrisJ,etal.Taverna:Atoolforthecompositionandenactmentofbioinformaticsworkflows[J].Bioinformatics,2004,20(17):3045-3054.

[4]RenK,ChenJ,XiaoN,etal.BuildingQuickServiceQuerylist(QSQL)tosupportautomatedservicediscoveryforscientificworkflow[J].Concurrency&ComputationPractice&Experience,2009,21(16):2099-2117.

[5]AaronWeiss.Computinginthecloud.net[J].Worker,2007,11(4):16-25.

[6]ZhangRui,WuK,WangJ.Onlineresourceschedulingunderconcavepricingforcloudcomputing[C]//QualityofService(IWQoS),22ndInternationalSymposiumofIEEE,2014:51-60.

[7]ZhaoY,LiYF,LuSY.Aserviceframeworkforscientificworkflowmanagementinthecloud[C]//IEEETransactionsonServicesComputing,2014:1-14.

[8]YuanD,YangY,LiuX,etal.Adataplacementstrategyinscientificcloudworkflows[J].FutureGenerationComputerSystems,2010,26(8):1200-1214.

[9]ZhangXY,TianY,JinY.AKneePointDrivenEvolutionaryAlgorithmforMany-ObjectiveOptimization[C].IEEETransactionsonEvolutionaryComputation,2014:1-17.

[10]ErDunZ,XingxingX,YiC.Adataplacementstrategybasedongeneticalgorithmforscientificworkflows[C]//ComputationalIntelligenceandSecurity(CIS), 2012EighthInternationalConference,Guangzhou,2012.IEEE,146-149.

[11]DengKF,SongJQ,RenKJ,etal.Graph-CutBasedCoschedulingStrategyTowardsEfficientExecutionofScientificWorkflowsinCollaborativeCloudEnvironments[C]//Proceedingsofthe2011IEEE/ACM12thInternationalConferenceonGridComputing,Lyon,2011:34-41.

[12]HerreroJG,BerlangaA,LopezJMM.EffectiveEvolutionaryAlgorithmsforMany-SpecificationsAttainment:ApplicationtoAirTrafficControlTrackingFilters[J].IEEETransactionsonEvolutionaryComputation,2009,13(1):151-168.

[13]PonsichA,JaimesAL,CoelloCAC.ASurveyonMultiobjectiveEvolutionaryAlgorithmsfortheSolutionofthePortfolioOptimizationProblemandOtherFinanceandEconomicsApplications[J].IEEETransactionsonEvolutionaryComputation,2013,17(3):321-344.

[14]HandlJ,KellDB,KnowlesJ.MultiobjectiveOptimizationinBioinformaticsandComputationalBiology[J].IEEE/ACMTransactionsonComputationalBiology&Bioinformatics,2007,4(2):279-292.

[15]DebK,PratapA,AgarwalS,etal.AFastAndElitistMultiobjectiveGeneticAlgorithm:NSGA-II[J].IEEETransactionsonEvolutionaryComputation,2002,6(2):182-197.

[16] 吉根林.遺傳算法研究綜述[J].計算機應用與軟件,2004,21(2):69-73.

[17]ZhouA,QuBY,LiH,etal.Multiobjectiveevolutionaryalgorithms:Asurveyofthestateoftheart[J].SwarmandEvolutionaryComputation,2011,1(1):32-49.

DATA PLACEMENT STRATEGY BASED ON MULTI-OBJECTIVE OPTIMIZATION FORSCIENTIFIC WORKFLOWS IN CLOUD COMPUTING ENVIRONMENT

Cheng Huimin1Li Xuejun1,2*Wu Yang1Zhu Erzhou2

1(SchoolofComputerScienceandTechnology,AnhuiUniversity,Hefei230601,Anhui,China)2(IntelligentComputingandSignalProcessingLaboratory,AnhuiUniversity,Hefei230039,Anhui,China)

The traditional data placement strategies for scientific workflows fail to monitor the load balancing between data centers while reducing the data transfer time. Thus, a data placement strategy based on multi-objective optimization is proposed. Firstly, the strategy generates the placement scheme of fixed datasets. Then it uses multi-objective optimization-based algorithm KnEA(Knee Point Driven Evolutionary Algorithm) to place flexible datasets, and then obtain the placement scheme of all datasets. The algorithm KnEA takes advantage of characteristic of knee points which can get good convergence comparing to other non-dominated sorting individuals, and comprehensively deals with the balance between multiple objectives. That’s why the data placement strategy is able to perform well in data transferring time and load balancing. The effectiveness of the proposed method is tested by comparison with two other strategies.

Cloud computing Scientific workflows Data placement Multi-objective optimization Load balancing

2015-10-16。國家自然科學

61300169)。程慧敏，碩士生，主研領域：云計算和科學工作流。李學俊，副教授。吳洋，碩士生。朱二周，講師。

TP393

A

10.3969/j.issn.1000-386x.2017.03.001